Espaço Banach - Banach space

Na matemática , mais especificamente na análise funcional , um espaço de Banach (pronuncia-se[ˈBanax] ) é um espaço vetorial normatizado completo . Assim, um espaço de Banach é um espaço vetorial com uma métrica que permite o cálculo do comprimento do vetor e da distância entre os vetores e é completo no sentido de que uma sequência de vetores de Cauchy sempre converge para um limite bem definidoque está dentro do espaço.

Os espaços de Banach foram nomeados em homenagem ao matemático polonês Stefan Banach , que introduziu esse conceito e o estudou sistematicamente em 1920–1922 junto com Hans Hahn e Eduard Helly . Maurice René Fréchet foi o primeiro a usar o termo "espaço de Banach" e Banach, por sua vez, cunhou o termo " espaço de Fréchet ". Os espaços de Banach surgiram originalmente do estudo de espaços funcionais por Hilbert , Fréchet e Riesz no início do século. Os espaços de Banach desempenham um papel central na análise funcional. Em outras áreas de análise , os espaços em estudo são frequentemente espaços de Banach.

Definição

Um espaço de Banach é um espaço normado completo Um espaço normado é um par que consiste em um espaço vetorial sobre um campo escalar K (onde K é ou ) junto com uma norma distinta Como todas as normas, esta norma induz uma função de distância invariante de translação , chamada de métrica canônica ou induzida ( norma ) , definida por ${\ displaystyle (X, \ | \ cdot \ |).}$${\ displaystyle (X, \ | \ cdot \ |)}$ ${\ displaystyle X}$${\ displaystyle \ mathbb {R}}$${\ displaystyle \ mathbb {C})}$ ${\ displaystyle \ | \ cdot \ |: X \ to \ mathbb {R}.}$

para todos os vetores Isso cria um espaço métrico Uma sequência é chamada -Cauchy ou Cauchy em ou -Cauchy se e somente se para cada real existe algum índice tal que ${\ displaystyle x, y \ in X.}$${\ displaystyle X}$ ${\ displaystyle (X, d).}$${\ displaystyle x _ {\ bullet} = \ left (x_ {n} \ right) _ {n = 1} ^ {\ infty}}$${\ displaystyle d}$ ${\ displaystyle (X, d)}$${\ displaystyle \ | \ cdot \ |}$${\ displaystyle r> 0,}$${\ displaystyle N}$

$${\ displaystyle d \ left (x_ {n}, x_ {m} \ right) = \ left \ | x_ {n} -x_ {m} \ right \ | <r}$$

sempre e são maiores que A métrica canónico é chamado uma métrica completa se o par é um espaço completo , o qual por meio de definição para cada - sequência de Cauchy no existe algum tal que ${\ displaystyle m}$${\ displaystyle n}$${\ displaystyle N.}$${\ displaystyle d}$${\ displaystyle (X, d)}$${\ displaystyle d}$ ${\ displaystyle x _ {\ bullet} = \ left (x_ {n} \ right) _ {n = 1} ^ {\ infty}}$${\ displaystyle (X, d),}$${\ displaystyle x \ in X}$

$${\ displaystyle \ lim _ {n \ to \ infty} \ left \ | x_ {n} -x \ right \ | = 0}$$

onde, porque a convergência desta sequência pode ser expressa de forma equivalente como: ${\ displaystyle \ left \ | x_ {n} -x \ right \ | = d \ left (x_ {n}, x \ right),}$

$${\ displaystyle \ lim _ {n \ to \ infty} x_ {n} = x \; {\ text {in}} (X, d).}$$

Por definição, o espaço normado é um

espaço de Banach se e somente se for um espaço métrico completo , ou dito de outra forma, se e somente se a métrica canônica for uma métrica completa . A norma de um espaço normalizado é chamada de${\ displaystyle (X, \ | \ cdot \ |)}$${\ displaystyle (X, d)}$${\ displaystyle d}$${\ displaystyle \ | \ cdot \ |}$${\ displaystyle (X, \ | \ cdot \ |)}$ norma completa se e somente sefor um espaço de Banach. ${\ displaystyle (X, \ | \ cdot \ |)}$

Produto L-semi-interno

Para qualquer espaço normalizado existe um produto

L-semi-interno ("L" é para Günter Lumer ) em tal que para todos ; em geral, pode haver um número infinito de produtos semi-internos em L que satisfaçam essa condição. Os produtos L-semi-inner são uma generalização dos produtos internos , que são o que distingue fundamentalmente os espaços Hilbert de todos os outros espaços Banach. Isso mostra que todos os espaços normados (e, portanto, todos os espaços de Banach) podem ser considerados generalizações de espaços (pré-) de Hilbert. ${\ displaystyle (X, \ | \ cdot \ |),}$${\ displaystyle \ langle \ cdot, \ cdot \ rangle}$${\ displaystyle X}$${\ textstyle \ | x \ | = {\ sqrt {\ langle x, x \ rangle}}}$${\ displaystyle x \ in X}$

Topologia

A métrica canônica de um espaço normado induz a

topologia métrica usual em que esta topologia , que é referida como topologia canônica ou induzida por norma , torna -se um espaço topológico metrizável de Hausdorff . Cada espaço normado é automaticamente assumido como portador dessa topologia, a menos que seja indicado o contrário. Com essa topologia, todo espaço de Banach é um espaço Baire , embora haja espaços normados que são Baire, mas não Banach. ${\ displaystyle d}$${\ displaystyle (X, \ | \ cdot \ |)}$ ${\ displaystyle \ tau _ {d}}$${\ displaystyle X,}$${\ displaystyle \ left (X, \ tau _ {d} \ right)}$

Esta topologia induzida por norma é invariante à translação, o que significa que para qualquer um e o subconjunto está

aberto (resp. Fechado ) em se e somente se isso for verdadeiro para Conseqüentemente, a topologia induzida por norma é completamente determinada por qualquer base de vizinhança na origem. Algumas bases de vizinhança comuns na origem incluem: ${\ displaystyle x \ in X}$${\ displaystyle S \ subseteq X,}$${\ displaystyle S}$${\ displaystyle X}$${\ displaystyle x + S: = \ {x + s: s \ in S \}.}$

$${\ displaystyle \ left \ {B_ {r}: r> 0 \ right \}, \ qquad \ left \ {{\ overline {B_ {r}}}: r> 0 \ right \}, \ qquad \ left \ {B_ {r_ {n}}: n \ in \ mathbb {N} \ right \}, \ qquad {\ text {ou}} \ qquad \ left \ {{\ overline {B_ {r_ {n}}}} : n \ in \ mathbb {N} \ right \}}$$

onde é qualquer sequência de números reais positivos que convergem para em (como por exemplo) e onde ${\ displaystyle \ left (r_ {i} \ right) _ {i = 1} ^ {\ infty}}$${\ displaystyle 0}$${\ displaystyle \ mathbb {R}}$${\ displaystyle r_ {n}: = 1 / n}$

$${\ displaystyle B_ {r}: = \ {x \ in X: \ | x \ | <r \} \ qquad {\ text {and}} \ qquad {\ overline {B_ {r}}}: = \ { x \ in X: \ | x \ | \ leq r \}}$$

são, respectivamente, a bola aberta e a bola fechada de raio centrado na origem. Assim, por exemplo, todo subconjunto aberto de pode ser escrito como uma união indexada por algum subconjunto onde todo é um inteiro; a bola fechada centrada na origem também pode ser usada em vez da bola aberta (embora o subconjunto e os inteiros possam precisar ser alterados). ${\ displaystyle r}$${\ displaystyle U}$${\ displaystyle X}$${\ displaystyle U = \ bigcup _ {u \ in I} \ left (u + B_ {1 / n_ {u}} \ right),}$${\ displaystyle I \ subseteq U,}$${\ displaystyle n_ {u}> 0}$${\ displaystyle {\ overline {B_ {1 / n_ {u}}}}}$${\ displaystyle I}$${\ displaystyle n_ {u}}$

Esta topologia induzida por norma também forma o que é conhecido como

espaço vetorial topológico (TVS), que por definição é um espaço vetorial dotado de uma topologia que torna as operações de adição e multiplicação escalar contínuas. Ressalta-se que o TVS é apenas um espaço vetorial junto com um determinado tipo de topologia; isto é, quando considerada como TVS, é não associada a qualquer norma específica ou métrica (ambos dos quais são " esquecidos "). ${\ displaystyle \ left (X, \ tau _ {d} \ right)}$${\ displaystyle \ left (X, \ tau _ {d} \ right)}$

Integridade

Normas completas e normas equivalentes

Duas normas em um espaço vetorial são chamadas de equivalentes se, e somente se, induzem a mesma topologia. Se e são duas normas equivalentes em um espaço vetorial, então é um espaço de Banach se e somente se for um espaço de Banach. Veja esta nota de rodapé para um exemplo de norma contínua em um espaço de Banach que

não é equivalente à norma dada a esse espaço de Banach. Todas as normas em um espaço vetorial de dimensão finita são equivalentes e todo espaço normado de dimensão finita é um espaço de Banach. ${\ displaystyle p}$${\ displaystyle q}$${\ displaystyle X}$${\ displaystyle (X, p)}$${\ displaystyle (X, q)}$

Normas completas vs métricas completas

Uma métrica em um espaço vetorial é induzida por uma norma sobre se e somente se a

translação é invariante e absolutamente homogênea , o que significa que para todos os escalares e todos , caso em que a função define uma norma sobre e a métrica canônica induzida por é igual a${\ displaystyle D}$${\ displaystyle X}$${\ displaystyle X}$${\ displaystyle D}$${\ displaystyle D (sx, sy) = | s | D (x, y)}$${\ displaystyle s}$${\ displaystyle x, y \ in X,}$${\ displaystyle \ | x \ |: = D (x, 0)}$${\ displaystyle X}$${\ displaystyle \ | \ cdot \ |}$${\ displaystyle D.}$

Suponha que seja um espaço normado e que seja a topologia norma induzida em Suponha que seja

qualquer métrica em tal que a topologia que induz seja igual a If é invariante à translação, então é um espaço de Banach se e somente se for um espaço métrico completo. Se é não invariante tradução, então pode ser possível para ser um espaço de Banach, mas para não ser um espaço completo (veja esta nota de rodapé para um exemplo). Em contraste, um teorema de Klee, que também se aplica a todos os espaços vetoriais topológicos metrizáveis , implica que, se existe alguma métrica completa em que induz a topologia norma em, então é um espaço de Banach. ${\ displaystyle (X, \ | \ cdot \ |)}$${\ displaystyle \ tau}$${\ displaystyle X.}$${\ displaystyle D}$ ${\ displaystyle X}$${\ displaystyle D}$${\ displaystyle X}$${\ displaystyle \ tau.}$${\ displaystyle D}$${\ displaystyle (X, \ | \ cdot \ |)}$${\ displaystyle (X, D)}$${\ displaystyle D}$${\ displaystyle (X, \ | \ cdot \ |)}$${\ displaystyle (X, D)}$${\ displaystyle D}$${\ displaystyle X}$${\ displaystyle X,}$${\ displaystyle (X, \ | \ cdot \ |)}$

Normas completas vs espaços vetoriais topológicos completos

Há outra noção de completude além da completude métrica, que é a noção de um espaço vetorial topológico completo (TVS) ou TVS-completude, que usa a teoria dos espaços uniformes . Especificamente, a noção de completude TVS usa uma uniformidade invariante de tradução única , chamada de uniformidade canônica , que depende apenas da subtração vetorial e da topologia que o espaço vetorial é dotado, e então em particular, esta noção de completude TVS é independente de qualquer norma induzida na topologia (e mesmo se aplica a TVSs que

nem mesmo são metrizáveis). Cada espaço de Banach é um TVS completo. Além disso, um espaço normado é um espaço de Banach (isto é, sua métrica induzida por norma é completa) se e somente se for completo como um espaço vetorial topológico. Se é um espaço vectorial topológico metrizáveis (onde nota que cada norma induzida topologia é metrizáveis), em seguida, é um TVS completas se e só se for um sequencialmente TVS completa, o que significa que é suficiente para verificar que todos os Cauchy sequência em converge na algum ponto de (isto é, não há necessidade de considerar a noção mais geral de redes de Cauchy arbitrárias ). ${\ displaystyle \ tau}$${\ displaystyle \ tau}$${\ displaystyle (X, \ tau)}$${\ displaystyle (X, \ tau)}$${\ displaystyle (X, \ tau)}$${\ displaystyle (X, \ tau)}$${\ displaystyle X}$

Se é um espaço vetorial topológico cuja

topologia é induzida por alguma norma (possivelmente desconhecida) , então é um espaço vetorial topológico completo se e somente se pode ser atribuída uma norma que induz na topologia e também torna um espaço de Banach. Um espaço vetorial topológico localmente convexo de Hausdorff é normable se e somente se seu espaço dual forte for normable, caso em que é um espaço de Banach ( denota o espaço dual forte de cuja topologia é uma generalização da topologia induzida por norma dual no dual contínuo espaço ; consulte esta nota de rodapé para obter mais detalhes). Se for um TVS localmente convexo metrizável , então será normal se e somente se for um espaço de Fréchet – Urysohn . Isso mostra que na categoria de TVSs localmente convexos , os espaços de Banach são exatamente aqueles espaços completos que são metrizáveis e têm espaços duais fortes metrizáveis . ${\ displaystyle (X, \ tau)}$${\ displaystyle (X, \ tau)}$${\ displaystyle X}$ ${\ displaystyle \ | \ cdot \ |}$${\ displaystyle X}$${\ displaystyle \ tau}$${\ displaystyle (X, \ | \ cdot \ |)}$ ${\ displaystyle X}$ ${\ displaystyle X_ {b} ^ {\ prime}}$${\ displaystyle X_ {b} ^ {\ prime}}$${\ displaystyle X_ {b} ^ {\ prime}}$${\ displaystyle X,}$ ${\ displaystyle X ^ {\ prime}}$${\ displaystyle X}$${\ displaystyle X}$${\ displaystyle X_ {b} ^ {\ prime}}$

Caracterização em termos de série

A estrutura do espaço vetorial permite relacionar o comportamento das sequências de Cauchy ao de séries convergentes

de vetores . Um espaço normado é um espaço de Banach se e somente se cada série absolutamente convergente em convergir em${\ displaystyle X}$${\ displaystyle X}$${\ displaystyle X,}$

$${\ displaystyle \ sum _ {n = 1} ^ {\ infty} \ | v_ {n} \ | <\ infty \ quad {\ text {implica que}} \ quad \ sum _ {n = 1} ^ {\ infty} v_ {n} \ \ {\ text {converge em}} \ \ X.}$$

Completações

Cada espaço normatizado pode ser isometricamente embutido em um denso subespaço vetorial de algum espaço de Banach, onde esse espaço de Banach é chamado de completamento do espaço normado. Esta completação de Hausdorff é única no isomorfismo isométrico .

Mais precisamente, para cada espaço normado existe um espaço de Banach e um mapeamento tal que é um

mapeamento isométrico e é denso em If é outro espaço de Banach tal que há um isomorfismo isométrico de um subconjunto denso de então isometricamente isomórfico a Este Banach o espaço é a conclusão do espaço normado O espaço métrico subjacente para é o mesmo que a conclusão métrica de com as operações do espaço vetorial estendidas de a A conclusão de é frequentemente denotada por${\ displaystyle X,}$${\ displaystyle Y}$${\ displaystyle T: X \ a Y}$${\ displaystyle T}$${\ displaystyle T (X)}$${\ displaystyle Y.}$${\ displaystyle Z}$${\ displaystyle X}$${\ displaystyle Z,}$${\ displaystyle Z}$${\ displaystyle Y.}$${\ displaystyle Y}$${\ displaystyle X.}$${\ displaystyle Y}$${\ displaystyle X,}$${\ displaystyle X}$${\ displaystyle Y.}$${\ displaystyle X}$${\ displaystyle {\ widehat {X}}.}$

Teoria geral

Operadores lineares, isomorfismos

Artigo principal: Operador limitado

Se X e Y são espaços normados sobre o mesmo campo de solo, o conjunto de todos os

mapas lineares contínuos é denotado por B ( X , Y ) . Em espaços de dimensão infinita, nem todos os mapas lineares são contínuos. Um mapeamento linear a partir de um espaço normalizado X para outro espaço normalizado é contínua se e só se for limitada no fechado bola unidade de X . Assim, o espaço vetorial B ( X , Y ) pode receber a norma do operador${\ displaystyle \ mathbb {K},}$ ${\ displaystyle \ mathbb {K}}$ ${\ displaystyle T: X \ a Y}$

Para Y um espaço de Banach, o espaço B ( X , Y ) é um espaço de Banach com relação a esta norma.

Se X é um espaço de Banach, o espaço forma uma álgebra de Banach unital ; a operação de multiplicação é dada pela composição de mapas lineares. ${\ displaystyle B (X) = B (X, X)}$

Se X e Y são espaços normados, eles são espaços normados isomórficos se existe uma bijeção linear tal que T e seu inverso são contínuos. Se um dos dois espaços X ou Y for completo (ou reflexivo , separável , etc.), o outro espaço também estará. Dois espaços normados X e Y são isometricamente isomorfo se em adição, T é um isometría , que é, para cada X em X . A distância Banach-Mazur entre dois espaços isomórficos, mas não isométricos X e Y, dá uma medida de quanto os dois espaços X e Y diferem. ${\ displaystyle T: X \ a Y}$${\ displaystyle T ^ {- 1}}$${\ displaystyle \ | T (x) \ | = \ | x \ |}$ ${\ displaystyle d (X, Y)}$

Funções lineares contínuas e limitadas e seminormas

Todo operador linear contínuo é um operador linear limitado e, se estiver lidando apenas com espaços normados, o inverso também é verdadeiro. Ou seja, um operador linear entre dois espaços normados é limitado se e somente se for uma função contínua . Então, em particular, porque o campo escalar (que é ou ) é um espaço normalizado, um funcional linear em um espaço normalizado é um funcional linear limitado se e somente se for um funcional linear contínuo . Isso permite que os resultados relacionados à continuidade (como os abaixo) sejam aplicados aos espaços de Banach. Embora delimitação seja o mesmo que continuidade para mapas lineares entre espaços normados, o termo "delimitado" é mais comumente usado quando se trata principalmente de espaços de Banach. ${\ displaystyle \ mathbb {R}}$${\ displaystyle \ mathbb {C}}$

Se for uma função subaditiva (como uma norma, uma função sublinear ou funcional linear real), então é contínua na origem se e somente se for uniformemente contínua em todos ; e se, além disso , é contínuo se e somente se seu valor absoluto for contínuo, o que acontece se e somente se for um subconjunto aberto de. Ao aplicar isso a ele, segue-se que a norma é sempre um mapa contínuo . E muito importante para a aplicação do teorema de Hahn-Banach , um funcional linear é contínuo se e somente se isso for verdadeiro para sua parte real e, além disso, e a parte real determina completamente, por isso que o teorema de Hahn-Banach é frequentemente afirmado apenas para o real funcionais lineares. Além disso, um funcional linear on é contínuo se e somente se o seminorm for contínuo, o que acontece se e somente se existe um seminorm contínuo tal que ; esta última afirmação envolvendo o funcional linear e a seminorma é encontrada em muitas versões do teorema de Hahn-Banach. ${\ displaystyle f: X \ to \ mathbb {R}}$${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle X}$${\ displaystyle f (0) = 0}$${\ displaystyle f}$ ${\ displaystyle | f |: X \ to [0, \ infty)}$${\ displaystyle \ {x \ in X: | f (x) | <1 \}}$${\ displaystyle X.}$${\ displaystyle f: = \ | \, \ cdot \, \ |,}$${\ displaystyle \ | \, \ cdot \, \ |: \ left (X, \ tau _ {d} \ right) \ to \ mathbb {R}}$${\ displaystyle f}$ ${\ displaystyle \ operatorname {Re} f}$${\ displaystyle \ | \ operatorname {Re} f \ | = \ | f \ |}$${\ displaystyle \ operatorname {Re} f}$ ${\ displaystyle f,}$${\ displaystyle f}$${\ displaystyle X}$ ${\ displaystyle | f |}$${\ displaystyle p: X \ to \ mathbb {R}}$${\ displaystyle | f | \ leq p}$${\ displaystyle f}$${\ displaystyle p}$

Noções básicas

O produto cartesiano de dois espaços normados não está canonicamente equipado com uma norma. No entanto, várias normas equivalentes são comumente usadas, como ${\ displaystyle X \ times Y}$

e dar origem a espaços normados isomórficos. Nesse sentido, o produto (ou a soma direta ) está completo se e somente se os dois fatores estiverem completos. ${\ displaystyle X \ times Y}$${\ displaystyle X \ oplus Y}$

Se H é um fechada subespaço linear de um espaço normalizado há uma norma natural no espaço quociente${\ displaystyle X,}$ ${\ displaystyle X / M,}$

O quociente é um espaço de Banach quando está completo. O mapa de quociente de até o envio para sua classe é linear, para e tem a norma 1 , exceto quando , nesse caso, o quociente é o espaço nulo. ${\ displaystyle X / M}$${\ displaystyle X}$${\ displaystyle X}$${\ displaystyle X / M,}$${\ displaystyle x \ in X}$${\ displaystyle x + M,}$${\ displaystyle M = X,}$

O subespaço linear fechado de é dito ser um subespaço complementado de se é o intervalo de uma projeção linear limitada sobreposta Neste caso, o espaço é isomorfo à soma direta de M e do núcleo da projeção${\ displaystyle M}$${\ displaystyle X}$${\ displaystyle X}$${\ displaystyle M}$ ${\ displaystyle P: X \ para M.}$${\ displaystyle X}$${\ displaystyle \ ker P,}$${\ displaystyle P.}$

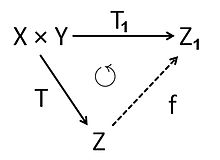
Suponha que e sejam espaços de Banach e que exista uma fatoração canônica de como ${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle T \ in B (X, Y).}$${\ displaystyle T}$

onde o primeiro mapa é o mapa de quociente e o segundo mapa envia todas as classes do quociente para a imagem em Isso está bem definido porque todos os elementos na mesma classe têm a mesma imagem. O mapeamento é uma bijeção linear de dentro do intervalo cujo inverso não precisa ser limitado. ${\ displaystyle \ pi}$${\ displaystyle T_ {1}}$${\ displaystyle x + \ ker T}$${\ displaystyle T (x)}$${\ displaystyle Y.,}$${\ displaystyle T_ {1}}$${\ displaystyle X / \ ker T}$${\ displaystyle T (X),}$

Espaços clássicos

Exemplos básicos de espaços de Banach incluem: os espaços Lp e seus casos especiais, os espaços de sequência que consistem em sequências escalares indexadas por números naturais ; entre eles, o espaço das sequências somaáveis ​​absolutamente e o espaço das sequências somadas quadradas; o espaço das sequências tendendo a zero e o espaço das sequências limitadas; o espaço de funções escalares contínuas em um espaço compacto de Hausdorff equipado com a norma máxima, ${\ displaystyle L ^ {p}}$ ${\ displaystyle \ ell ^ {p}}$ ${\ displaystyle \ mathbb {N}}$${\ displaystyle \ ell ^ {1}}$${\ displaystyle \ ell ^ {2}}$${\ displaystyle c_ {0}}$${\ displaystyle \ ell ^ {\ infty}}$${\ displaystyle C (K)}$${\ displaystyle K,}$

De acordo com o teorema de Banach-Mazur , cada espaço de Banach é isometricamente isomórfico a um subespaço de alguns. Para cada espaço de Banach X separável , há um subespaço fechado de tal que${\ displaystyle C (K).}$${\ displaystyle M}$${\ displaystyle \ ell ^ {1}}$${\ displaystyle X: = \ ell ^ {1} / M.}$

Qualquer espaço de Hilbert serve como exemplo de espaço de Banach. Um espaço de Hilbert em está completo para uma norma do formulário ${\ displaystyle H}$${\ displaystyle \ mathbb {K} = \ mathbb {R}, \ mathbb {C}}$

Onde é o produto interno , linear em seu primeiro argumento que satisfaz o seguinte:

${\ displaystyle {\ begin {alinhado} \ langle y, x \ rangle & = {\ overline {\ langle x, y \ rangle}}, \ quad {\ text {for all}} x, y \ in H \\ \ langle x, x \ rangle & \ geq 0, \ quad {\ text {para todos}} x \ in H \\\ langle x, x \ rangle = 0 {\ text {se e somente se}} x & = 0 . \ end {alinhado}}}$

Por exemplo, o espaço é um espaço de Hilbert. ${\ displaystyle L ^ {2}}$

Os espaços de Hardy , os espaços de Sobolev são exemplos de espaços de Banach que estão relacionados com espaços e têm estrutura adicional. Eles são importantes em diferentes ramos de análise, análise harmônica e equações diferenciais parciais, entre outros. ${\ displaystyle L ^ {p}}$

Álgebras de Banach

Uma álgebra de Banach é um espaço de Banach acima ou junto com uma estrutura de álgebra , de forma que o mapa do produto seja contínuo. Uma norma equivalente pode ser encontrada para que para todos${\ displaystyle A}$${\ displaystyle \ mathbb {K} = \ mathbb {R}}$${\ displaystyle \ mathbb {C},}$${\ displaystyle \ mathbb {K}}$${\ displaystyle A \ times A \ ni (a, b) \ mapsto ab \ in A}$${\ displaystyle A}$${\ displaystyle \ | ab \ | \ leq \ | a \ | \ | b \ |}$${\ displaystyle a, b \ in A.}$

Exemplos

• O espaço de Banach com o produto pontual é uma álgebra de Banach.${\ displaystyle C (K)}$
• A álgebra disco Um ( D ) consiste de funções holomorfos no disco unidade aberta e contínuos no seu encerramento : D . Equipado com a norma máxima em D , a álgebra de disco A ( D ) é uma subálgebra fechada de C ( D ) .${\ displaystyle D \ subseteq \ mathbb {C}}$
• A álgebra de Wiener A ( T ) é a álgebra de funções no círculo unitário T com séries de Fourier absolutamente convergentes. Por meio do mapa que associa uma função em T à sequência de seus coeficientes de Fourier, essa álgebra é isomórfica à álgebra de Banach, onde o produto é a convolução das sequências.${\ displaystyle \ ell ^ {1} (Z),}$
• Para cada espaço de Banach X , o espaço B ( X ) de operadores lineares limitados em X , com a composição de mapas como produto, é uma álgebra de Banach.
• Uma álgebra C * é uma álgebra de Banach complexa A com uma involução antilinear tal que o espaço B ( H ) de operadores lineares limitados em um espaço de Hilbert H é um exemplo fundamental de álgebra C *. O teorema de Gelfand-Naimark afirma que toda C * -álgebra é isomórfica isomorficamente a uma C * -subálgebra de algum B ( H ) . O espaço de funções contínuas complexas em um espaço de Hausdorff compacto é um exemplo de álgebra C * comutativa, onde a involução associa a cada função seu conjugado complexo ${\ displaystyle a \ mapsto a ^ {*}}$${\ displaystyle \ left \ | a ^ {*} a \ right \ | = \ | a \ | ^ {2}.}$${\ displaystyle C (K)}$${\ displaystyle K}$${\ displaystyle f}$ ${\ displaystyle {\ overline {f}}.}$

Espaço duplo

Se X for um espaço normalizado e o campo subjacente (os números reais ou complexos ), o espaço dual contínuo é o espaço de mapas lineares contínuos de X para ou funcionais lineares contínuos . A notação para o dual contínuo está neste artigo. Desde é um espaço de Banach (usando o valor absoluto como norma), a dupla X  ' é um espaço de Banach, para cada espaço normalizado X . ${\ displaystyle \ mathbb {K}}$${\ displaystyle \ mathbb {K},}$${\ displaystyle X ^ {\ prime} = B (X, \ mathbb {K})}$${\ displaystyle \ mathbb {K}}$

A principal ferramenta para provar a existência de funcionais lineares contínuos é o teorema de Hahn-Banach .

Teorema de Hahn-Banach. Seja X um espaço vetorial sobre o campo. Vamos além ${\ displaystyle \ mathbb {K} = \ mathbb {R}, \ mathbb {C}.}$

• ${\ displaystyle Y \ subseteq X}$ser um subespaço linear ,
• ${\ displaystyle p: X \ to \ mathbb {R}}$ser uma função sublinear e
• ${\ displaystyle f: Y \ to \ mathbb {K}}$ser um funcional linear de modo que para todos os y em Y .${\ displaystyle \ operatorname {Re} (f (y)) \ leq p (y)}$

Então, existe um funcional linear para que${\ displaystyle F: X \ to \ mathbb {K}}$

$${\ displaystyle F {\ big \ vert} _ {Y} = f, \ quad {\ text {e}} \ quad {\ text {para todos}} x \ em X, \ \ \ operatorname {Re} (F (x)) \ leq p (x).}$$

Em particular, todo funcional linear contínuo em um subespaço de um espaço normado pode ser estendido continuamente a todo o espaço, sem aumentar a norma do funcional. Um caso especial importante é o seguinte: para cada vetor x em um espaço normado X , existe um funcional linear contínuo em X tal que ${\ displaystyle f}$

Quando x não é igual ao vetor 0 , o funcional deve ter a norma um e é chamado de funcional de norma para x . ${\ displaystyle f}$

O teorema da separação de Hahn-Banach afirma que dois conjuntos convexos não vazios disjuntos em um espaço de Banach real, um deles aberto, podem ser separados por um hiperplano afim fechado . O conjunto convexo aberto fica estritamente de um lado do hiperplano, o segundo conjunto convexo fica do outro lado, mas pode tocar o hiperplano.

Um subconjunto S num espaço de Banach X é totais , se a extensão linear de S é densa em X . O subconjunto S é total em X se e somente se o único funcional linear contínuo que desaparece em S é o funcional 0 : esta equivalência segue do teorema de Hahn-Banach.

Se X é a soma de duas directa fechado linear subespaços M e N , em seguida, a dupla X  ' de X é isomorfa a soma directa dos duos de M e N . Se M é um subespaço linear fechado em X , pode-se associar o ortogonal de M no dual,

O ortogonal é um subespaço linear fechado do dual. O dual de M é isometricamente isomórfico a O dual de é isometricamente isomórfico a${\ displaystyle M ^ {\ bot}}$${\ displaystyle X ^ {\ prime} / M ^ {\ bot}.}$${\ displaystyle X / M}$${\ displaystyle M ^ {\ bot}.}$

O dual de um espaço de Banach separável não precisa ser separável, mas:

Teorema. Seja X um espaço normalizado. Se X  ′ é separável , então X é separável.

Quando X  ' é separável, o critério acima para a totalidade pode ser utilizado para demonstrar a existência de um subconjunto total de contáveis em X .

Topologias fracas

A topologia fraca em um espaço de Banach X é a topologia mais grosseira em X para a qual todos os elementos no espaço dual contínuo são contínuos. A topologia normal é, portanto, mais precisa do que a topologia fraca. Segue do teorema de separação de Hahn-Banach que a topologia fraca é Hausdorff , e que um subconjunto convexo de norma fechada de um espaço de Banach também é fracamente fechado. Um mapa linear norma-contínuo entre dois espaços de Banach X e Y também é fracamente contínua , isto é, contínua a partir da topologia de fraco X para que de Y . ${\ displaystyle x ^ {\ prime}}$${\ displaystyle X ^ {\ prime}}$

Se X tem dimensão infinita, existem mapas lineares que não são contínuos. O espaço de todos os mapas lineares de X ao campo subjacente (este espaço é chamado de espaço dual algébrico , para distingui-lo também induz uma topologia em X que é mais fina do que a topologia fraca e muito menos usada na análise funcional. ${\ displaystyle X ^ {*}}$${\ displaystyle \ mathbb {K}}$${\ displaystyle X ^ {*}}$${\ displaystyle X ^ {\ prime}}$

Em um espaço dual , há uma topologia mais fraca do que a topologia fraca de X  ′ , chamada topologia fraca * . É a topologia mais grosseira para a qual todos os mapas de avaliação onde os intervalos são contínuos. Sua importância vem do teorema de Banach – Alaoglu . ${\ displaystyle X ^ {\ prime}}$${\ displaystyle X ^ {\ prime}}$${\ displaystyle x ^ {\ prime} \ in X ^ {\ prime} \ mapsto x ^ {\ prime} (x),}$${\ displaystyle x}$${\ displaystyle X,}$

Teorema de Banach – Alaoglu. Seja X um espaço vetorial normalizado . Então, a esfera unitária fechada do espaço dual é compacta na topologia fraca *. ${\ displaystyle B = \ left \ {x \ in X: \ | x \ | \ leq 1 \ right \}}$

O teorema de Banach-Alaoglu pode ser provado usando o teorema de Tychonoff sobre produtos infinitos de espaços compactos de Hausdorff. Quando X é separável, a esfera unitária B  ′ do dual é um compacto metrizável na topologia fraca *.

Exemplos de espaços duplos

O dual de é isometricamente isomórfico a : para cada funcional linear limitado em, há um elemento único tal que ${\ displaystyle c_ {0}}$${\ displaystyle \ ell ^ {1}}$${\ displaystyle f}$${\ displaystyle c_ {0},}$${\ displaystyle y = \ left \ {y_ {n} \ right \} \ in \ ell ^ {1}}$

O dual de é isometricamente isomórfico a }. O dual do espaço de Lebesgue é isometricamente isomórfico para quando e${\ displaystyle \ ell ^ {1}}$${\ displaystyle \ ell ^ {\ infty}}$ ${\ displaystyle L ^ {p} ([0,1])}$${\ displaystyle L ^ {q} ([0,1])}$${\ displaystyle 1 \ leq p <\ infty}$${\ displaystyle {\ frac {1} {p}} + {\ frac {1} {q}} = 1.}$

Para cada vetor em um espaço de Hilbert, o mapeamento ${\ displaystyle y}$${\ displaystyle H,}$

define um funcional linear contínuo em O teorema da representação de Riesz afirma que todo funcional linear contínuo em H tem a forma de um vetor definido exclusivamente em O mapeamento é uma bijeção isométrica antilinear de H em seu H  ′ dual . Quando os escalares são reais, este mapa é um isomorfismo isométrico. ${\ displaystyle f_ {y}}$${\ displaystyle H.}$${\ displaystyle f_ {y}}$${\ displaystyle y}$${\ displaystyle H.}$${\ displaystyle y \ in H \ a f_ {y}}$

Quando é um espaço topológico de Hausdorff compacto, o dual de é o espaço de medidas de Radon no sentido de Bourbaki. O subconjunto P ( K ) de M ( K ) que consiste em medidas não negativas de massa 1 ( medidas de probabilidade ) é um subconjunto w * fechado convexo da bola unitária de M ( K ) . Os pontos extremos de P ( K ) são as medidas de Dirac sobre K . O conjunto de medidas de Dirac sobre K , equipadas com a w * -topology, é homeomorfo ao K . ${\ displaystyle K}$${\ displaystyle M (K)}$${\ displaystyle C (K)}$

Teorema de Banach-Stone. Se K e L são espaços de Hausdorff compactos e seesão isomórficos isomórficos, então os espaços topológicos K e L são homeomórficos .${\ displaystyle C (K)}$${\ displaystyle C (L)}$

O resultado foi estendido por Amir e Cambern para o caso em que a distância multiplicativa de Banach-Mazur entre e é <2 . O teorema não é mais verdadeiro quando a distância é = 2 . ${\ displaystyle C (K)}$${\ displaystyle C (L)}$

Na álgebra de Banach comutativa, os ideais máximos são precisamente os núcleos das medidas de Dirac em K , ${\ displaystyle C (K),}$

De forma mais geral, pelo teorema de Gelfand-Mazur , os ideais máximos de uma álgebra de Banach comutativa unital podem ser identificados com seus caracteres - não apenas como conjuntos, mas como espaços topológicos: o primeiro com a topologia do casco e o último com w * -topologia. Nessa identificação, o espaço ideal máximo pode ser visto como um subconjunto aw * -compacto da bola unitária no A  ′ dual .

Teorema. Se K é um espaço compacto de Hausdorff, então o máximo espaço ideal Ξ da álgebra de Banach é homeomorfo ao K .${\ displaystyle C (K)}$

Nem todo unital comutativa Banach álgebra é da forma por algum compacto Hausdorff espaço K . No entanto, esta afirmação é válida se alguém colocar na categoria menor das álgebras C * comutativas . O teorema de representação de Gelfand para C * -álgebras comutativas afirma que toda C * -álgebra A comutativa unital é isometricamente isomórfica a um espaço. O espaço compacto de Hausdorff K aqui é novamente o espaço ideal máximo, também chamado de espectro de A no contexto da álgebra C *. ${\ displaystyle C (K)}$${\ displaystyle C (K)}$ ${\ displaystyle C (K)}$

Bidual

Se X é um espaço normalizado, o dual (contínuo) do dual é chamado${\ displaystyle X ^ {\ prime \ prime}}$${\ displaystyle X ^ {\ prime}}$bidual , ousegundo dual de Para cada espaço normadoX, há um mapa natural, ${\ displaystyle X.}$

Isso se define como um funcional linear contínuo ou seja, um elemento de O mapa é um mapa linear de X a Como consequência da existência de um funcional de norma para cada mapa isométrico, portanto injetivo . ${\ displaystyle F_ {X} (x)}$${\ displaystyle X ^ {\ prime},}$${\ displaystyle X ^ {\ prime \ prime}.}$${\ displaystyle F_ {X}: x \ a F_ {X} (x)}$${\ displaystyle X ^ {\ prime \ prime}.}$ ${\ displaystyle f}$${\ displaystyle x \ in X,}$${\ displaystyle F_ {X}}$

Por exemplo, o dual de é identificado com e o dual de é identificado com o espaço de sequências escalares limitadas. Sob essas identificações, o mapa de inclusão de a É realmente isométrico, mas não em. ${\ displaystyle X = c_ {0}}$${\ displaystyle \ ell ^ {1},}$${\ displaystyle \ ell ^ {1}}$${\ displaystyle \ ell ^ {\ infty},}$${\ displaystyle F_ {X}}$${\ displaystyle c_ {0}}$${\ displaystyle \ ell ^ {\ infty}.}$

Se for sobrejetivo , então o espaço normado X é denominado reflexivo (veja abaixo ). Sendo o dual de um espaço normatizado, o bidual é completo, portanto, todo espaço normativo reflexivo é um espaço de Banach. ${\ displaystyle F_ {X}}$${\ displaystyle X ^ {\ prime \ prime}}$

Usando a incorporação isométrica , é comum considerar um espaço normado X como um subconjunto de seu bidual. Quando X é um espaço de Banach, ele é visto como um subespaço linear fechado de Se X não é reflexiva, a bola unidade de X é um subconjunto adequado da bola unitária de Os Goldstine teorema afirma que a bola unidade de um espaço normal é fracamente * -densa na bola unitária do bidual. Ou seja, para cada no bidual existe uma rede em X para que ${\ displaystyle F_ {X},}$${\ displaystyle X ^ {\ prime \ prime}.}$${\ displaystyle X ^ {\ prime \ prime}.}$${\ displaystyle x ^ {\ prime \ prime}}$ ${\ displaystyle \ left (x_ {i} \ right) _ {i \ in I}}$

A rede pode ser substituída por uma sequência ligeiramente * -convergente quando o dual é separável. Por outro lado, os elementos do bidual de que não estão em não podem ser fracos * -limite de sequências em, uma vez que é sequencialmente completo fracamente . ${\ displaystyle X ^ {\ prime}}$${\ displaystyle \ ell ^ {1}}$${\ displaystyle \ ell ^ {1}}$${\ displaystyle \ ell ^ {1},}$${\ displaystyle \ ell ^ {1}}$

Teoremas de Banach

Aqui estão os principais resultados gerais sobre os espaços de Banach que remontam à época do livro de Banach (Banach (1932) ) e estão relacionados ao teorema da categoria de Baire . De acordo com este teorema, um espaço métrico completo (como um espaço de Banach, um espaço de Fréchet ou um espaço F ) não pode ser igual a uma união de contáveis ​​subconjuntos fechados com interiores vazios . Portanto, um espaço de Banach não pode ser a união de muitos subespaços fechados contáveis, a menos que já seja igual a um deles; um espaço de Banach com uma base de Hamel contável é de dimensão finita.

Teorema de Banach – Steinhaus. Seja X um espaço de Banach e Y um espaço vetorial normatizado . Suponha-se que F é uma colecção de operadores lineares contínuas a partir de X para Y . O princípio de limite uniforme afirma que se para todo x em X temosentão${\ displaystyle \ sup _ {T \ in F} \ | T (x) \ | _ {Y} <\ infty,}$${\ displaystyle \ sup _ {T \ in F} \ | T \ | _ {Y} <\ infty.}$

O teorema de Banach-Steinhaus não se limita a espaços de Banach. Pode ser estendido, por exemplo, ao caso em que X é um espaço de Fréchet , desde que a conclusão seja modificada da seguinte forma: sob a mesma hipótese, existe uma vizinhança U de 0 em X de modo que todos os T em F são uniformemente limitados em U ,

O Teorema do Mapeamento Aberto. Sejam X e Y espaços de Banach eum operador linear contínuo sobrejetivo, então T é um mapa aberto.${\ displaystyle T: X \ a Y}$

Corolário. Cada operador linear limitado um-para-um de um espaço de Banach para um espaço de Banach é um isomorfismo.

O primeiro teorema do isomorfismo para espaços de Banach. Suponha-se que X e Y são Banach espaços e que Suponha-se ainda que o intervalo de T é fechada em Y . Então é isomórfico para${\ displaystyle T \ in B (X, Y).}$${\ displaystyle X / \ ker T}$${\ displaystyle T (X).}$

Este resultado é uma consequência direta do teorema do isomorfismo de Banach anterior e da fatoração canônica de mapas lineares limitados.

Corolário. Se um espaço de Banach X é a soma direta interna de subespaços fechados, então X é isomórfico a${\ displaystyle M_ {1}, \ ldots, M_ {n},}$${\ displaystyle M_ {1} \ oplus \ cdots \ oplus M_ {n}.}$

Esta é outra consequência do teorema do isomorfismo de Banach, aplicado à bijeção contínua de em X enviando para a soma${\ displaystyle M_ {1} \ oplus \ cdots \ oplus M_ {n}}$${\ displaystyle m_ {1}, \ cdots, m_ {n}}$${\ displaystyle m_ {1} + \ cdots + m_ {n}.}$

O Teorema do Grafo Fechado. LetSer um mapeamento linear entre espaços de Banach. O gráfico de T é fechado emse e somente se T for contínuo.${\ displaystyle T: X \ a Y}$${\ displaystyle X \ times Y}$

Reflexividade

O espaço normado X é chamado reflexivo quando o mapa natural

é sobrejetiva. Os espaços normativos reflexivos são espaços de Banach.

Teorema. Se X é um espaço de Banach reflexivo, todo subespaço fechado de X e todo espaço quociente de X são reflexivos.

Isso é uma consequência do teorema de Hahn-Banach. Além disso, pelo teorema do mapeamento aberto, se houver um operador linear limitado do espaço de Banach X para o espaço de Banach Y , então Y é reflexivo.

Teorema. Se X for um espaço de Banach, então X será reflexivo se e somente se X  ′ for reflexivo.

Corolário. Seja X um espaço de Banach reflexivo. Então X é separável se e somente se X  ′ é separável.

De fato, se o dual Y  ′ de um espaço de Banach Y é separável, então Y é separável. Se X é reflexivo e separável, então o dual de X  ′ é separável, então X  ′ é separável.

Teorema. Suponha que sejam espaços normados e que Então X seja reflexivo se e somente se cada um for reflexivo.${\ displaystyle X_ {1}, \ ldots, X_ {n}}$${\ displaystyle X = X_ {1} \ oplus \ cdots \ oplus X_ {n}.}$${\ displaystyle X_ {j}}$

Os espaços de Hilbert são reflexivos. Os espaços L ^p são reflexivos quando Mais geralmente, espaços uniformemente convexos são reflexivos, pelo teorema de Milman-Pettis . Os espaços não são reflexivos. Nestes exemplos de espaços não-reflexiva X , o bidual X  '' é "muito maior" do que X . Ou seja, sob a incorporação isométrica natural de X em X  ′ ′ dada pelo teorema de Hahn-Banach, o quociente X  ′ ′ /  X é infinito dimensional, e até mesmo não separável. No entanto, Robert C. James construiu um exemplo de um espaço não reflexivo, geralmente chamado de " o espaço de James " e denotado por J , de modo que o quociente J  ′ ′ /  J é unidimensional. Além disso, este espaço J é isometricamente isomórfico ao seu bidual. ${\ displaystyle 1 <p <\ infty.}$${\ displaystyle c_ {0}, \ ell ^ {1}, L ^ {1} ([0,1]), C ([0,1])}$

Teorema. Um espaço X de Banach é reflexivo se e somente se sua bola unitária for compacta na topologia fraca .

Quando X é reflexivo, segue-se que todos os subconjuntos convexos fechados e limitados de X são fracamente compactos. Em um espaço de Hilbert H , a compactação fraca da bola unitária é freqüentemente usada da seguinte maneira: toda sequência limitada em H tem subsequências convergentes fracamente.

A fraca compactação da esfera unitária fornece uma ferramenta para encontrar soluções em espaços reflexivos para certos problemas de otimização . Por exemplo, cada convexa função contínua sobre a bola unidade B de um espaço reflexiva alcança o seu valor mínimo em algum ponto em B .

Tal como um caso especial do resultado anterior, quando X é um espaço reflexiva sobre cada funcional linear contínua no X  ' atinge o seu máximo na bola unidade de X . O seguinte teorema de Robert C. James fornece uma afirmação inversa. ${\ displaystyle \ mathbb {R},}$${\ displaystyle f}$${\ displaystyle \ | f \ |}$

Teorema de James. Para um espaço de Banach, as duas propriedades a seguir são equivalentes:

• X é reflexivo.
• para todos no existe com modo que${\ displaystyle f}$${\ displaystyle X ^ {\ prime}}$${\ displaystyle x \ in X}$${\ displaystyle \ | x \ | \ leq 1,}$${\ displaystyle f (x) = \ | f \ |.}$

O teorema pode ser estendido para fornecer uma caracterização de conjuntos convexos fracamente compactos.

Em cada espaço X não reflexivo de Banach , existem funcionais lineares contínuos que não atingem a norma . No entanto, o Bispo - Phelps teorema afirma que functionals-alcançar norma são densos norma na dupla X  ' de X .

Convergências fracas de sequências

Uma sequência em um espaço de Banach X é fracamente convergente para um vetor se converge para para cada funcional linear contínuo no dual X  ′ . A sequência é uma sequência de Cauchy fracamente se converge para um limite escalar , para todo em X  ′ . Uma sequência na dupla X  ' é fracamente * convergente para um funcional se converge para para cada X em X . Sequências fracamente de Cauchy, sequências fracamente convergentes e fracamente * convergentes são limitadas por norma, como consequência do teorema de Banach-Steinhaus . ${\ displaystyle \ left \ {x_ {n} \ right \}}$${\ displaystyle x \ in X}$${\ displaystyle \ left \ {f \ left (x_ {n} \ right) \ right \}}$${\ displaystyle f (x)}$${\ displaystyle f}$${\ displaystyle \ left \ {x_ {n} \ right \}}$${\ displaystyle \ left \ {f \ left (x_ {n} \ right) \ right \}}$${\ displaystyle L (f),}$${\ displaystyle f}$${\ displaystyle \ left \ {f_ {n} \ right \}}$${\ displaystyle f \ in X ^ {\ prime}}$${\ displaystyle f_ {n} (x)}$${\ displaystyle f (x)}$

Quando a sequência em X é uma sequência de Cauchy fraca, o limite L acima define um funcional linear limitado no dual X  ′ , ou seja, um elemento L do bidual de X , e L é o limite de na topologia * fraca do bidual. O Banach espaço X é fracamente sequencialmente completa se cada sequência de Cauchy fracamente é convergente fracamente em X . Conclui-se da discussão anterior que os espaços reflexivos são fracamente sequencialmente completos. ${\ displaystyle \ left \ {x_ {n} \ right \}}$${\ displaystyle \ left \ {x_ {n} \ right \}}$

Teorema. Para cada medida, o espaço é fracamente sequencialmente completo.${\ displaystyle \ mu,}$${\ displaystyle L ^ {1} (\ mu)}$

Uma sequência ortonormal em um espaço de Hilbert é um exemplo simples de uma sequência convergente fraca, com limite igual ao vetor 0 . A base do vetor unitário de para ou de é outro exemplo de sequência fracamente nula , ou seja, uma sequência que converge fracamente para 0 . Para cada seqüência nula fraca em um espaço de Banach, existe uma seqüência de combinações convexas de vetores da seqüência dada que converge para 0 em norma . ${\ displaystyle \ ell ^ {p}}$${\ displaystyle 1 <p <\ infty,}$${\ displaystyle c_ {0},}$

A base do vetor unitário de não é fracamente Cauchy. As sequências de Cauchy fracamente em são fracamente convergentes, uma vez que os espaços L ¹ são fracamente sequencialmente completos. Na verdade, as sequências fracamente convergentes em são convergentes à norma. Isso significa que satisfaz a propriedade de Schur . ${\ displaystyle \ ell ^ {1}}$${\ displaystyle \ ell ^ {1}}$${\ displaystyle \ ell ^ {1}}$${\ displaystyle \ ell ^ {1}}$

Resultados envolvendo a base${\ displaystyle \ ell ^ {1}}$

As sequências fracamente de Cauchy e a base são os casos opostos da dicotomia estabelecida no seguinte resultado profundo de H. P. Rosenthal. ${\ displaystyle \ ell ^ {1}}$

Teorema. Let Ser uma seqüência limitada em um espaço de Banach. Ou tem uma subsequência de Cauchy fracamente, ou admite uma subsequência equivalente à base do vetor unitário padrão de${\ displaystyle \ left \ {x_ {n} \ right \} _ {n \ in \ mathbb {N}}}$${\ displaystyle \ left \ {x_ {n} \ right \} _ {n \ in \ mathbb {N}}}$${\ displaystyle \ ell ^ {1}.}$

Um complemento a esse resultado deve-se a Odell e Rosenthal (1975).

Teorema. Seja X um espaço de Banach separável. Os seguintes são equivalentes:

• O espaço X não contém um subespaço fechado isomórfico para${\ displaystyle \ ell ^ {1}.}$
• Cada elemento do bidual X  '' é a fraca * -limit de uma sequência em X .${\ displaystyle \ left \ {x_ {n} \ right \}}$

Pelo teorema Goldstine, cada elemento da unidade bola B  '' do X  '' é fraca * -limit de uma rede na bola unitária de X . Quando X não contém todos os elementos de B  '' é fraco * -limit de uma sequência na bola unidade de X . ${\ displaystyle \ ell ^ {1},}$

Quando o espaço de Banach X é separável, a bola unitária do dual X  ′ , equipado com a topologia fraca *, é um espaço compacto metrizável K , e cada elemento x  ′ ′ no bidual X  ′ ′ define uma função limitada em K :

Esta função é contínua para a topologia compacta de K se e somente se x  ′ ′ estiver realmente em X , considerado como um subconjunto de X  ′ ′ . Suponha, além disso, para o resto do parágrafo que X não contém. Pelo resultado anterior de Odell e Rosenthal, a função x  ′ ′ é o limite pontual em K de uma sequência de funções contínuas em K , portanto, é uma primeira classe de Baire função na K . A bola unidade do bidual é um subconjunto compacto pontual da primeira classe Baire em K . ${\ displaystyle \ ell ^ {1}.}$${\ displaystyle \ left \ {x_ {n} \ right \} \ subseteq X}$

Sequências, compactação fraca e fraca *

Quando X é separável, a bola unitária do dual é fraca * -compactada por Banach – Alaoglu e metrizável para a topologia fraca *, portanto, cada sequência limitada no dual tem subseqüências fracamente * convergentes. Isso se aplica a espaços reflexivos separáveis, mas mais é verdade neste caso, conforme declarado abaixo.

A topologia fraca de um espaço de Banach X é metrizável se e somente se X tiver dimensão finita. Se o X  ′ dual é separável, a topologia fraca da bola unitária de X é metrizável. Isso se aplica em particular a espaços reflexivos de Banach separáveis. Embora a topologia fraca da esfera unitária não seja metrizável em geral, pode-se caracterizar a compactação fraca usando sequências.

Teorema de Eberlein – Šmuliano . Um conjunto A em um espaço de Banach é relativamente fracamente compacto se e somente se cada sequência { a _n } em A tiver uma subseqüência fracamente convergente.

Um espaço de Banach X é reflexivo se e somente se cada sequência limitada em X tem uma subsequência fracamente convergente.

Um subconjunto A em fracamente compacto é compacto em norma. De fato, toda sequência em A tem subsequências convergentes fracamente por Eberlein – Šmulian, que são convergentes norma pela propriedade de Schur de${\ displaystyle \ ell ^ {1}}$${\ displaystyle \ ell ^ {1}.}$

Bases Schauder

Uma base de Schauder em um espaço de Banach X é uma sequência de vetores em X com a propriedade de que para cada vetor x em X , existem escalares exclusivamente definidos dependendo de x , de modo que ${\ displaystyle \ left \ {e_ {n} \ right \} _ {n \ geq 0}}$${\ displaystyle \ left \ {x_ {n} \ right \} _ {n \ geq 0}}$

Os espaços de Banach com uma base de Schauder são necessariamente separáveis , porque o conjunto contável de combinações lineares finitas com coeficientes racionais (digamos) é denso.

Segue-se a partir do Teorema de Banach-Steinhaus que os mapeamentos lineares { P _n } são uniformemente limitada por uma constante C . Deixe { e^∗
_n} denotam os funcionais de coordenada que atribuem a cada x em X a coordenada de x na expansão acima. Eles são chamados de funcionais bi-ortogonais . Quando os vetores de base têm norma 1 , os funcionais coordenados { e${\ displaystyle x_ {n}}$^∗
_n} Tem norma na dupla de X . ${\ displaystyle \, \ leq 2C}$

A maioria dos espaços separáveis ​​clássicos tem bases explícitas. O sistema Haar é uma base para O sistema trigonométrico é uma base em L ^p ( T ) quando O sistema de Schauder é uma base no espaço C ([0, 1]) . A questão de saber se a álgebra de disco A ( D ) tem uma base permaneceu em aberto por mais de quarenta anos, até que Bočkarev mostrou em 1974 que A ( D ) admite uma base construída a partir do sistema de Franklin . ${\ displaystyle \ left \ {h_ {n} \ right \}}$${\ displaystyle L ^ {p} ([0,1]), 1 \ leq p <\ infty.}$${\ displaystyle 1 <p <\ infty.}$

Como todo vetor x em um espaço de Banach X com uma base é o limite de P _n ( x ) , com P _n de classificação finita e uniformemente limitado, o espaço X satisfaz a propriedade de aproximação limitada . O primeiro exemplo de Enflo de um espaço sem a propriedade de aproximação foi, ao mesmo tempo, o primeiro exemplo de um espaço de Banach separável sem uma base de Schauder.

Robert C. James caracterizou a reflexividade em espaços de Banach com uma base: o espaço X com uma base de Schauder é reflexivo se e somente se a base estiver encolhendo e limitadamente completa . Neste caso, os funcionais biortogonais formar uma base da dupla de X .

Produto tensor

Let and be two -vector space. O produto tensorial de e é um espaço -vetorial com um mapeamento bilinear que possui a seguinte propriedade universal : ${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle \ mathbb {K}}$ ${\ displaystyle X \ otimes Y}$${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle \ mathbb {K}}$${\ displaystyle Z}$${\ displaystyle T: X \ vezes Y \ a Z}$

Se houver algum mapeamento bilinear em um espaço vetorial, então existe um mapeamento linear único, de modo que${\ displaystyle T_ {1}: X \ vezes Y \ a Z_ {1}}$${\ displaystyle \ mathbb {K}}$${\ displaystyle Z_ {1},}$${\ displaystyle f: Z \ a Z_ {1}}$${\ displaystyle T_ {1} = f \ circ T.}$

A imagem abaixo de um casal em é denotada por e chamada de tensor simples . Cada elemento em é uma soma finita desses tensores simples. ${\ displaystyle T}$${\ displaystyle (x, y)}$${\ displaystyle X \ times Y}$${\ displaystyle x \ otimes y,}$${\ displaystyle z}$${\ displaystyle X \ otimes Y}$

Existem várias normas que podem ser colocadas no produto tensorial dos espaços vetoriais subjacentes, entre outras, a norma cruzada projetiva e a norma cruzada injetiva introduzidas por A. Grothendieck em 1955.

Em geral, o produto tensorial de espaços completos não é completo novamente. Ao trabalhar com espaços de Banach, costuma-se dizer que o produto tensorial projetivo de dois espaços de Banach e é a complementação do produto tensorial algébrico equipado com a norma tensorial projetiva, e da mesma forma para o produto tensor injetivo Grothendieck provou em particular que ${\ displaystyle X}$${\ displaystyle Y}$ ${\ displaystyle X {\ widehat {\ otimes}} _ {\ pi} Y}$${\ displaystyle X \ otimes Y}$ ${\ displaystyle X {\ widehat {\ otimes}} _ {\ varejpsilon} Y.}$

${\ displaystyle {\ begin {alinhado} C (K) {\ widehat {\ otimes}} _ {\ varejpsilon} Y & \ simeq C (K, Y), \\ L ^ {1} ([0,1]) {\ widehat {\ otimes}} _ {\ pi} Y & \ simeq L ^ {1} ([0,1], Y), \ end {alinhado}}}$

onde está um espaço de Hausdorff compacto, o espaço de Banach de funções contínuas de para e o espaço de funções mensuráveis ​​e integráveis ​​de Bochner de para e onde os isomorfismos são isométricos. Os dois isomorfismos acima são as respectivas extensões do mapa enviando o tensor para a função de valor vetorial${\ displaystyle K}$${\ displaystyle C (K, Y)}$${\ displaystyle K}$${\ displaystyle Y}$${\ displaystyle L ^ {1} ([0,1], Y)}$${\ displaystyle [0,1]}$${\ displaystyle Y,}$${\ displaystyle f \ otimes y}$${\ displaystyle s \ in K \ a f (s) y \ in Y.}$

Produtos tensores e a propriedade de aproximação

Deixe ser um espaço de Banach. O produto tensorial é identificado isometricamente com o fechamento do conjunto de operadores de classificação finita. Quando tem a propriedade de aproximação , este fechamento coincide com o espaço dos operadores compactos em${\ displaystyle X}$${\ displaystyle X '{\ widehat {\ otimes}} _ {\ varepsilon} X}$${\ displaystyle B (X)}$${\ displaystyle X}$${\ displaystyle X.}$

Para cada espaço de Banach existe um mapa linear de norma natural${\ displaystyle Y,}$${\ displaystyle 1}$

obtido estendendo o mapa de identidade do produto tensorial algébrico. Grothendieck relacionou o problema de aproximação à questão de se este mapa é um-para-um quando é o dual de Precisamente, para cada espaço de Banach o mapa ${\ displaystyle Y}$${\ displaystyle X.}$${\ displaystyle X,}$ é um para um se, e somente se, tiver a propriedade de aproximação. ${\ displaystyle X}$

Grothendieck conjeturou que e deve ser diferente sempre que e forem espaços de Banach de dimensão infinita. Isso foi refutado por Gilles Pisier em 1983. Pisier construiu um espaço de Banach de dimensão infinita tal que e são iguais. Além disso, assim como no exemplo do Enflo , este espaço é um espaço "feito à mão" que não possui a propriedade de aproximação. Por outro lado, Szankowski provou que o espaço clássico não possui a propriedade de aproximação. ${\ displaystyle X {\ widehat {\ otimes}} _ {\ pi} Y}$${\ displaystyle X {\ widehat {\ otimes}} _ {\ varepsilon} Y}$${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle X}$${\ displaystyle X {\ widehat {\ otimes}} _ {\ pi} X}$${\ displaystyle X {\ widehat {\ otimes}} _ {\ varepsilon} X}$${\ displaystyle X}$${\ displaystyle B \ left (\ ell ^ {2} \ right)}$

Alguns resultados de classificação

Caracterizações do espaço de Hilbert entre espaços de Banach

Uma condição necessária e suficiente para que a norma de um espaço de Banach seja associada a um produto interno é a identidade do paralelogramo : ${\ displaystyle X}$

para todos ${\ displaystyle x, y \ in X: \ qquad \ | x + y \ | ^ {2} + \ | xy \ | ^ {2} = 2 \ left (\ | x \ | ^ {2} + \ | y \ | ^ {2} \ right).}$

Segue-se, por exemplo, que o espaço de Lebesgue é um espaço de Hilbert apenas quando Se essa identidade for satisfeita, o produto interno associado é dado pela identidade de polarização . No caso de escalares reais, isso dá: ${\ displaystyle L ^ {p} ([0,1])}$${\ displaystyle p = 2.}$

Para escalares complexos, definir o produto interno de modo a ser -linear em antilinear na identidade de polarização dá: ${\ displaystyle \ mathbb {C}}$${\ displaystyle x,}$ ${\ displaystyle y,}$

Para ver que a lei do paralelogramo é suficiente, observa-se no caso real que é simétrico, e no caso complexo, que ela satisfaz a propriedade de simetria Hermitiana e a lei do paralelogramo implica que é aditiva em Segue-se que é linear sobre os racionais , portanto, linear por continuidade. ${\ displaystyle \ langle x, y \ rangle}$${\ displaystyle \ langle ix, y \ rangle = i \ langle x, y \ rangle.}$${\ displaystyle \ langle x, y \ rangle}$${\ displaystyle x.}$

Várias caracterizações de espaços isomórficos (ao invés de isométricos) para espaços de Hilbert estão disponíveis. A lei do paralelogramo pode ser estendida a mais de dois vetores e enfraquecida pela introdução de uma desigualdade bilateral com uma constante : Kwapień provou que se ${\ displaystyle c \ geq 1}$

para cada inteiro e todas as famílias de vetores , o espaço X de Banach é isomorfo a um espaço de Hilbert. Aqui, denota a média sobre as escolhas possíveis de sinais. No mesmo artigo, Kwapień provou que a validade de um teorema de Parseval com valor de Banach para a transformada de Fourier caracteriza os espaços de Banach isomórficos aos espaços de Hilbert. ${\ displaystyle n}$${\ displaystyle \ left \ {x_ {1}, \ ldots, x_ {n} \ right \} \ subseteq X,}$${\ displaystyle \ operatorname {Ave} _ {\ pm}}$${\ displaystyle 2 ^ {n}}$${\ displaystyle \ pm 1.}$

Lindenstrauss e Tzafriri provaram que um espaço de Banach no qual todo subespaço linear fechado é complementado (ou seja, é o intervalo de uma projeção linear limitada) é isomórfico a um espaço de Hilbert. A prova baseia-se no teorema de Dvoretzky sobre seções euclidianas de corpos convexos simétricos

centrais de alta dimensão. Em outras palavras, o teorema de Dvoretzky afirma que, para cada inteiro, qualquer espaço normado de dimensão finita, com dimensão suficientemente grande em comparação com contém subespaços quase isométricos ao espaço euclidiano dimensional. ${\ displaystyle n,}$${\ displaystyle n,}$${\ displaystyle n}$

O próximo resultado fornece a solução do chamado problema de espaço homogêneo . Um espaço de Banach de dimensão infinita é considerado

homogêneo se for isomórfico a todos os seus subespaços fechados de dimensão infinita. Um espaço de Banach isomorfo a é homogêneo, e Banach pediu o contrário. ${\ displaystyle X}$${\ displaystyle \ ell ^ {2}}$

Teorema. Um espaço de Banach isomorfo a todos os seus subespaços fechados de dimensão infinita é isomorfo a um espaço de Hilbert separável.

Um espaço de Banach de dimensão infinita é hereditariamente indecomponível quando nenhum subespaço dele pode ser isomórfico à soma direta de dois espaços de Banach de dimensão infinita. O teorema da dicotomia de Gowers afirma que todo espaço de Banach de dimensão infinita X contém, ou um subespaço Y com base incondicional , ou um subespaço Z hereditariamente indecomponível e, em particular, Z não é isomórfico aos seus hiperplanos fechados. Se X é homogêneo, ele deve, portanto, ter uma base incondicional. Conclui-se então da solução parcial obtida por Komorowski e Tomczak – Jaegermann , para espaços com uma base incondicional, que X é isomorfo a${\ displaystyle \ ell ^ {2}.}$

Classificação métrica

Se for uma

isometria do espaço de Banach para o espaço de Banach (onde e são espaços vetoriais terminados ), então o teorema de Mazur-Ulam afirma que deve ser uma transformação afim. Em particular, se isso for mapeado de zero a zero, então deve ser linear. Este resultado implica que a métrica em espaços de Banach, e mais geralmente em espaços normados, captura completamente sua estrutura linear. ${\ displaystyle T: X \ a Y}$${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle \ mathbf {R}}$${\ displaystyle T}$${\ displaystyle T (0_ {X}) = 0_ {Y},}$${\ displaystyle T}$${\ displaystyle X}$${\ displaystyle Y,}$${\ displaystyle T}$

Classificação topológica

Espaços de Banach de dimensão finita são homeomórficos como espaços topológicos, se e somente se eles têm a mesma dimensão que espaços vetoriais reais.

O teorema de Anderson-Kadec (1965–66) prova que quaisquer dois espaços de Banach separáveis ​​de dimensão infinita são homeomórficos como espaços topológicos. O teorema de Kadec foi estendido por Torunczyk, que provou que quaisquer dois espaços de Banach são homeomórficos se e somente se eles tiverem o mesmo caráter de densidade , a cardinalidade mínima de um subconjunto denso.

Espaços de funções contínuas

Quando dois espaços compactos de Hausdorff e são

homeomórficos , os espaços de Banach e são isométricos. Por outro lado, quando não é homeomórfico à distância (multiplicativa) de Banach – Mazur entre e deve ser maior ou igual a 2 , veja acima os resultados de Amir e Cambern . Embora incontáveis ​​espaços métricos compactos possam ter diferentes tipos de homeomorfia, um tem o seguinte resultado devido a Milutin: ${\ displaystyle K_ {1}}$${\ displaystyle K_ {2}}$${\ displaystyle C \ left (K_ {1} \ right)}$${\ displaystyle C \ left (K_ {2} \ right)}$${\ displaystyle K_ {1}}$${\ displaystyle K_ {2},}$${\ displaystyle C \ left (K_ {1} \ right)}$${\ displaystyle C \ left (K_ {2} \ right)}$

Teorema. Seja K um incontável espaço métrico compacto. Então é isomórfico para ${\ displaystyle C (K)}$${\ displaystyle C ([0,1]).}$

A situação é diferente para espaços compactos de Hausdorff contáveis ​​e infinitos . Cada K compacto infinito contável é homeomórfico a algum intervalo fechado de números ordinais

${\ displaystyle \ langle 1, \ alpha \ rangle = \ {\ gamma \: \ 1 \ leq \ gamma \ leq \ alpha \}}$

equipado com a topologia de ordem , onde é um ordinal infinito contável. O espaço de Banach é então isométrico para

C (<1, α  >) . Quando são dois ordinais infinitos contáveis, e assumindo que os espaços C (<1, α  >) e C (<1, β  >) são isomórficos se e somente se β < α ^ω . Por exemplo, os espaços de Banach ${\ displaystyle \ alpha}$${\ displaystyle C (K)}$${\ displaystyle \ alpha, \ beta}$${\ displaystyle \ alpha \ leq \ beta,}$

$${\ displaystyle C (\ langle 1, \ omega \ rangle), \ C (\ langle 1, \ omega ^ {\ omega} \ rangle), \ C (\ langle 1, \ omega ^ {\ omega ^ {2} } \ rangle), \ C (\ langle 1, \ omega ^ {\ omega ^ {3}} \ rangle), \ cdots, C (\ langle 1, \ omega ^ {\ omega ^ {\ omega}} \ rangle ), \ cdots}$$

são mutuamente não isomórficos.

Exemplos

Artigo principal: Lista de espaços de Banach

Glossário de símbolos para a tabela abaixo:

• ${\ displaystyle \ mathbb {F}}$denota o campo de números reais ou

números complexos${\ displaystyle \ mathbb {R}}$ ${\ displaystyle \ mathbb {C}.}$

${\ displaystyle K}$é um espaço compacto de Hausdorff .

${\ displaystyle p, q \ in \ mathbb {R}}$são números reais com que são conjugados de Hölder , o que significa que eles satisfazem e, portanto, também${\ displaystyle 1 <p, q <\ infty}$${\ displaystyle {\ frac {1} {q}} + {\ frac {1} {p}} = 1}$${\ displaystyle q = {\ frac {p} {p-1}}.}$

${\ displaystyle \ Sigma}$é uma -álgebra de conjuntos.${\ displaystyle \ sigma}$

${\ displaystyle \ Xi}$é uma álgebra de conjuntos (para espaços que requerem apenas aditividade finita, como o espaço ba ).

${\ displaystyle \ mu}$é uma medida com variação Uma medida positiva é uma função de conjunto positivo de valor real definida em uma -álgebra que é contável aditiva.${\ displaystyle | \ mu |.}$${\ displaystyle \ sigma}$

Espaços clássicos de Banach
	Espaço duplo	Reflexivo	fracamente completo sequencialmente	Norma		Notas
${\ displaystyle \ mathbb {F} ^ {n}}$	${\ displaystyle \ mathbb {F} ^ {n}}$	sim	sim	${\ displaystyle \ | x \ | _ {2}}$	${\ displaystyle = \ left (\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {2} \ right) ^ {1/2}}$	Espaço euclidiano
${\ displaystyle \ ell _ {p} ^ {n}}$	${\ displaystyle \ ell _ {q} ^ {n}}$	sim	sim	${\ displaystyle \ | x \ | _ {p}}$	${\ displaystyle = \ left (\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {p} \ right) ^ {\ frac {1} {p}}}$
${\ displaystyle \ ell _ {\ infty} ^ {n}}$	${\ displaystyle \ ell _ {1} ^ {n}}$	sim	sim	${\ displaystyle \ | x \ | _ {\ infty}}$	${\ displaystyle = \ max \ nolimits _ {1 \ leq i \ leq n} | x_ {i} |}$
${\ displaystyle \ ell ^ {p}}$	${\ displaystyle \ ell ^ {q}}$	sim	sim	${\ displaystyle \ | x \ | _ {p}}$	${\ displaystyle = \ left (\ sum _ {i = 1} ^ {\ infty} | x_ {i} | ^ {p} \ right) ^ {\ frac {1} {p}}}$
${\ displaystyle \ ell ^ {1}}$	${\ displaystyle \ ell ^ {\ infty}}$	Não	sim	${\ displaystyle \ | x \ | _ {1}}$	${\ displaystyle = \ sum _ {i = 1} ^ {\ infty} \ left | x_ {i} \ right |}$
${\ displaystyle \ ell ^ {\ infty}}$	${\ displaystyle \ operatorname {ba}}$	Não	Não	${\ displaystyle \ | x \ | _ {\ infty}}$	${\ displaystyle = \ sup \ nolimits _ {i} \ left | x_ {i} \ right |}$
${\ displaystyle \ operatorname {c}}$	${\ displaystyle \ ell ^ {1}}$	Não	Não	${\ displaystyle \ | x \ | _ {\ infty}}$	${\ displaystyle = \ sup \ nolimits _ {i} \ left | x_ {i} \ right |}$
${\ displaystyle c_ {0}}$	${\ displaystyle \ ell ^ {1}}$	Não	Não	${\ displaystyle \ | x \ | _ {\ infty}}$	${\ displaystyle = \ sup \ nolimits _ {i} \ left | x_ {i} \ right |}$	Isomórfico, mas não isométrico para ${\ displaystyle c.}$
${\ displaystyle \ operatorname {bv}}$	${\ displaystyle \ ell ^ {\ infty}}$	Não	sim	${\ displaystyle \ | x \ | _ {bv}}$	${\ displaystyle = \ left | x_ {1} \ right | + \ sum _ {i = 1} ^ {\ infty} \ left | x_ {i + 1} -x_ {i} \ right |}$	Isometricamente isomórfico para ${\ displaystyle \ ell ^ {1}.}$
${\ displaystyle \ operatorname {bv} _ {0}}$	${\ displaystyle \ ell ^ {\ infty}}$	Não	sim	${\ displaystyle \ | x \ | _ {bv_ {0}}}$	${\ displaystyle = \ sum _ {i = 1} ^ {\ infty} \ left | x_ {i + 1} -x_ {i} \ right |}$	Isometricamente isomórfico para ${\ displaystyle \ ell ^ {1}.}$
${\ displaystyle \ operatorname {bs}}$	${\ displaystyle \ operatorname {ba}}$	Não	Não	${\ displaystyle \ | x \ | _ {bs}}$	${\ displaystyle = \ sup \ nolimits _ {n} \ left | \ sum _ {i = 1} ^ {n} x_ {i} \ right |}$	Isometricamente isomórfico para ${\ displaystyle \ ell ^ {\ infty}.}$
${\ displaystyle \ operatorname {cs}}$	${\ displaystyle \ ell ^ {1}}$	Não	Não	${\ displaystyle \ | x \ | _ {bs}}$	${\ displaystyle = \ sup \ nolimits _ {n} \ left | \ sum _ {i = 1} ^ {n} x_ {i} \ right |}$	Isometricamente isomórfico para ${\ displaystyle c.}$
${\ displaystyle B (K, \ Xi)}$	${\ displaystyle \ operatorname {ba} (\ Xi)}$	Não	Não	${\ displaystyle \ | f \ | _ {B}}$	${\ displaystyle = \ sup \ nolimits _ {k \ in K} | f (k) |}$
${\ displaystyle C (K)}$	${\ displaystyle \ operatorname {rca} (K)}$	Não	Não	${\ displaystyle \ | x \ | _ {C (K)}}$	${\ displaystyle = \ max \ nolimits _ {k \ in K} | f (k) |}$
${\ displaystyle \ operatorname {ba} (\ Xi)}$	?	Não	sim	${\ displaystyle \ | \ mu \ | _ {ba}}$	${\ displaystyle = \ sup \ nolimits _ {S \ in \ Sigma} | \ mu | (S)}$
${\ displaystyle \ operatorname {ca} (\ Sigma)}$	?	Não	sim	${\ displaystyle \ | \ mu \ | _ {ba}}$	${\ displaystyle = \ sup \ nolimits _ {S \ in \ Sigma} | \ mu | (S)}$	Um subespaço fechado de ${\ displaystyle \ operatorname {ba} (\ Sigma).}$
${\ displaystyle \ operatorname {rca} (\ Sigma)}$	?	Não	sim	${\ displaystyle \ | \ mu \ | _ {ba}}$	${\ displaystyle = \ sup \ nolimits _ {S \ in \ Sigma} | \ mu | (S)}$	Um subespaço fechado de ${\ displaystyle \ operatorname {ca} (\ Sigma).}$
${\ displaystyle L ^ {p} (\ mu)}$	${\ displaystyle L ^ {q} (\ mu)}$	sim	sim	${\ displaystyle \ | f \ | _ {p}}$	${\ displaystyle = \ left (\ int | f | ^ {p} \, d \ mu \ right) ^ {\ frac {1} {p}}}$
${\ displaystyle L ^ {1} (\ mu)}$	${\ displaystyle L ^ {\ infty} (\ mu)}$	Não	sim	${\ displaystyle \ | f \ | _ {1}}$	${\ displaystyle = \ int | f | \, d \ mu}$	O dual é se for -finito . ${\ displaystyle L ^ {\ infty} (\ mu)}$${\ displaystyle \ mu}$${\ displaystyle \ sigma}$
${\ displaystyle \ operatorname {BV} ([a, b])}$	?	Não	sim	${\ displaystyle \ | f \ | _ {BV}}$	${\ displaystyle = V_ {f} ([a, b]) + \ lim \ nolimitos _ {x \ a ^ {+}} f (x)}$	${\ displaystyle V_ {f} ([a, b]).}$é a variação total de${\ displaystyle f}$
${\ displaystyle \ operatorname {NBV} ([a, b])}$	?	Não	sim	${\ displaystyle \ | f \ | _ {BV}}$	${\ displaystyle = V_ {f} ([a, b])}$	${\ displaystyle \ operatorname {NBV} ([a, b])}$consiste em funções tais que${\ displaystyle \ operatorname {BV} ([a, b])}$${\ displaystyle \ lim \ nolimits _ {x \ to a ^ {+}} f (x) = 0}$
${\ displaystyle \ operatorname {AC} ([a, b])}$	${\ displaystyle \ mathbb {F} + L ^ {\ infty} ([a, b])}$	Não	sim	${\ displaystyle \ | f \ | _ {BV}}$	${\ displaystyle = V_ {f} ([a, b]) + \ lim \ nolimitos _ {x \ a ^ {+}} f (x)}$	Isomórfico ao espaço de Sobolev ${\ displaystyle W ^ {1,1} ([a, b]).}$
${\ displaystyle C ^ {n} ([a, b])}$	${\ displaystyle \ operatorname {rca} ([a, b])}$	Não	Não	${\ displaystyle \ | f \ |}$	${\ displaystyle = \ sum _ {i = 0} ^ {n} \ sup \ nolimits _ {x \ in [a, b]} \ left | f ^ {(i)} (x) \ right |}$	Isomórfico a essencialmente pelo teorema de Taylor . ${\ displaystyle \ mathbb {R} ^ {n} \ oplus C ([a, b]),}$

Derivados

Vários conceitos de uma derivada podem ser definidos em um espaço de Banach. Consulte os artigos sobre o derivado Fréchet e o derivado Gateaux para obter detalhes. A derivada de Fréchet permite uma extensão do conceito de derivada total aos espaços de Banach. A derivada Gateaux permite uma extensão de uma derivada direcional para espaços vetoriais topológicos localmente convexos . A diferenciabilidade de Fréchet é uma condição mais forte do que a diferenciabilidade de Gateaux. A quase-derivada é outra generalização da derivada direcional que implica uma condição mais forte do que a diferenciabilidade de Gateaux, mas uma condição mais fraca do que a diferenciabilidade de Fréchet.

Generalizações

Vários espaços importantes em análise funcional, por exemplo, o espaço de todas as funções infinitamente muitas vezes diferenciável ou o espaço de todas as distribuições sobre estão completas, mas não são normed espaços vetoriais e, portanto, não espaços de Banach. Nos espaços Fréchet ainda se tem uma métrica completa , enquanto os espaços LF são espaços vetoriais uniformes completos que surgem como limites dos espaços Fréchet. ${\ displaystyle \ mathbb {R} \ to \ mathbb {R},}$${\ displaystyle \ mathbb {R},}$

Veja também

• Espaço (matemática)  - Conjunto matemático com alguma estrutura adicionada
  • Espaço Fréchet  - Um espaço vetorial topológico localmente convexo que também é um espaço métrico completo
  • Espaço Hardy
  • Espaço de Hilbert  - Generalização do espaço euclidiano permitindo dimensões infinitas
  • Produto L-semi-interno  - Generalização de produtos internos que se aplica a todos os espaços normados
  • ${\ displaystyle L ^ {p}}$espaço  - espaços de função generalizando espaços de norma p de dimensão finita
  • Espaço de Sobolev  - espaço de funções de Banach com norma combinando L ^p -normas da função e seus derivados
  • Malha de Banach
• Problema de distorção
• Espaço de interpolação
• Espaço vetorial topológico localmente convexo  - Um espaço vetorial com uma topologia definida por conjuntos abertos convexos
• Espaço Smith
• Espaço vetorial topológico  - espaço vetorial com noção de proximidade

Notas

Referências

Bibliografia

• Banach, Stefan (1932). Théorie des Opérations Linéaires [ Teoria das Operações Lineares ] (PDF) . Monografie Matematyczne (em francês). 1 . Warszawa: Subwencji Funduszu Kultury Narodowej. Zbl  0005.20901 . Arquivado do original (PDF) em 11/01/2014 . Página visitada em 2020-07-11 .
• Beauzamy, Bernard (1985) [1982], Introduction to Banach Spaces and their Geometry (Segunda edição revisada), North-Holland.
• Bourbaki, Nicolas (1987) [1981]. Certos espaces topologiques de vetoriais [ Topological Vector Spaces: Capítulos 1–5 ]. Annales de l'Institut Fourier . Éléments de mathématique . 2 . Traduzido por Eggleston, HG; Madan, S. Berlin New York: Springer-Verlag. ISBN 978-3-540-42338-6. OCLC  17499190 .
• Carothers, Neal L. (2005), Um curso de curta duração sobre a teoria do espaço de Banach , London Mathematical Society Student Texts, 64 , Cambridge: Cambridge University Press, pp. Xii + 184, ISBN 0-521-84283-2.
• Conway, John (1990). Um curso de análise funcional . Textos de Pós-Graduação em Matemática . 96 (2ª ed.). Nova York: Springer-Verlag . ISBN 978-0-387-97245-9. OCLC  21195908 .
• Diestel, Joseph (1984), Sequences and series in Banach spaces , Graduate Texts in Mathematics, 92 , Nova York: Springer-Verlag, pp.  Xii + 261 , ISBN 0-387-90859-5.
• Dunford, Nelson; Schwartz, Jacob T. com a assistência de WG Bade e RG Bartle (1958), Linear Operators. I. General Theory , Pure and Applied Mathematics, 7 , Nova York: Interscience Publishers, Inc., MR  0117523
• Edwards, Robert E. (1995). Análise Funcional: Teoria e Aplicações . Nova York: Dover Publications. ISBN 978-0-486-68143-6. OCLC  30593138 .
• Grothendieck, Alexander (1973). Espaços vetoriais topológicos . Traduzido por Chaljub, Orlando. Nova York: Gordon and Breach Science Publishers. ISBN 978-0-677-30020-7. OCLC  886098 .
• Jarchow, Hans (1981). Espaços localmente convexos . Stuttgart: BG Teubner. ISBN 978-3-519-02224-4. OCLC  8210342 .
• Khaleelulla, SM (1982). Contra-exemplos em espaços vetoriais topológicos . Notas de aula em matemática . 936 . Berlin, Heidelberg, New York: Springer-Verlag . ISBN 978-3-540-11565-6. OCLC  8588370 .
• Köthe, Gottfried (1983) [1969]. Espaço vectorial topológico I . Grundlehren der mathematischen Wissenschaften. 159 . Traduzido por Garling, DJH Nova York: Springer Science & Business Media. ISBN 978-3-642-64988-2. MR  0248498 . OCLC  840293704 .
• Lindenstrauss, Joram ; Tzafriri, Lior (1977), Classical Banach Spaces I, Sequence Spaces , Ergebnisse der Mathematik und ihrer Grenzgebiete, 92 , Berlin: Springer-Verlag, ISBN 3-540-08072-4.
• Megginson, Robert E. (1998), Uma introdução à teoria do espaço de Banach , Graduate Texts in Mathematics, 183 , Nova York: Springer-Verlag, pp. Xx + 596, ISBN 0-387-98431-3.
• Narici, Lawrence ; Beckenstein, Edward (2011). Espaços vetoriais topológicos . Matemática pura e aplicada (segunda edição). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC  144216834 .
• Robertson, Alex P .; Robertson, Wendy J. (1980). Espaços vetoriais topológicos . Cambridge Tracts in Mathematics . 53 . Cambridge England: Cambridge University Press . ISBN 978-0-521-29882-7. OCLC  589250 .
• Rudin, Walter (1991). Análise funcional . Série Internacional em Matemática Pura e Aplicada. 8 (segunda edição). New York, NY: McGraw-Hill Science / Engineering / Math . ISBN 978-0-07-054236-5. OCLC  21163277 .
• Ryan, Raymond A. (2002), Introduction to Tensor Products of Banach Spaces , Springer Monographs in Mathematics, Londres: Springer-Verlag, pp. Xiv + 225, ISBN 1-85233-437-1.
• Schaefer, Helmut H .; Wolff, Manfred P. (1999). Espaços vetoriais topológicos . GTM . 8 (segunda edição). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC  840278135 .
• Swartz, Charles (1992). Uma introdução à Análise Funcional . Nova York: M. Dekker. ISBN 978-0-8247-8643-4. OCLC  24909067 .
• Trèves, François (2006) [1967]. Espaços Vetoriais Topológicos, Distribuições e Kernels . Mineola, NY: Dover Publications. ISBN 978-0-486-45352-1. OCLC  853623322 .
• Wilansky, Albert (2013). Métodos modernos em espaços vetoriais topológicos . Mineola, Nova York: Dover Publications, Inc. ISBN 978-0-486-49353-4. OCLC  849801114 .
• Wojtaszczyk, Przemysław (1991), espaços de Banach para analistas , Cambridge Studies in Advanced Mathematics, 25 , Cambridge: Cambridge University Press, pp. Xiv + 382, ISBN 0-521-35618-0.

links externos

• "Banach space" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Espaço Banach" . MathWorld .