Teorema de Stokes generalizado - Generalized Stokes theorem

Parte de uma série de artigos sobre
Cálculo
Teorema fundamental Regra integral de Leibniz Limites de funções Continuidade Teorema do valor médio Teorema de Rolle
Diferencial Definições Derivado  ( generalizações ) Diferencial infinitesimal de uma função total Conceitos Notação de diferenciação Segunda derivada Diferenciação implícita Diferenciação logarítmica Taxas relacionadas Teorema de Taylor Regras e identidades Soma produtos Cadeia Poder Quociente Regra de L'Hôpital Inverso General Leibniz Fórmula de Faà di Bruno Reynolds
Integrante Listas de integrais Transformada integral Definições Antiderivado Integral  ( impróprio ) Integral de Riemann Integração Lebesgue Integração de contorno Integral de funções inversas Integração por Peças Discos Conchas cilíndricas Substituição  ( trigonométrica , Weierstrass , Euler ) Fórmula de Euler Frações Parciais Mudança de ordem Fórmulas de redução Diferenciando sob o signo integral Algoritmo de Risch
Series Geométrico  ( aritmético-geométrico ) Harmônico Alternando Poder Binomial Taylor Testes de convergência Limite de soma (teste de termo) Razão Raiz Integrante Comparação direta Limite de comparação Série alternada Condensação de Cauchy Dirichlet Abel
Vetor Gradiente Divergência Ondulação Laplaciano Derivada direcional Identidades Teoremas Gradiente Green's Stokes ' Divergência Stokes generalizado
Multivariável Formalismos Matriz Tensor Exterior Geométrico Definições Derivativo parcial Integral múltiplo Integral de linha Integral de superfície Volume integral Jacobiano Hessian
Especializado Fracionário Malliavin Estocástico Variações
Diversos Pré-cálculo História Glossário Lista de tópicos Integração Bee Análise
v t e

No cálculo vetorial e na geometria diferencial, o teorema de Stokes generalizado (às vezes com apóstrofo como teorema de Stokes ou teorema de Stokes ), também chamado de teorema de Stokes-Cartan , é uma afirmação sobre a integração de formas diferenciais em variedades , que simplifica e generaliza vários teoremas do cálculo vetorial . É uma generalização do teorema fundamental do cálculo de Isaac Newton que relaciona integrais de linha bidimensionais a integrais de superfície tridimensionais.

O teorema de Stokes diz que a integral de uma forma diferencial ω sobre a fronteira de alguma variedade orientável Ω é igual à integral de sua derivada externa dω sobre o todo de Ω , ou seja,

${\ displaystyle \ int _ {\ partial \ Omega} \ omega = \ int _ {\ Omega} d \ omega \ ,.}$

O teorema de Stokes foi formulado em sua forma moderna por Élie Cartan em 1945, após trabalhos anteriores sobre a generalização dos teoremas do cálculo vetorial de Vito Volterra , Édouard Goursat e Henri Poincaré .

Esta forma moderna do teorema de Stokes é uma vasta generalização de um resultado clássico que Lord Kelvin comunicou a George Stokes em uma carta datada de 2 de julho de 1850. Stokes definiu o teorema como uma pergunta no exame do Prêmio Smith de 1854 , que levou ao resultado levando seu nome. Foi publicado pela primeira vez por Hermann Hankel em 1861. Este teorema clássico de Kelvin-Stokes relaciona a integral de superfície da curvatura de um campo vetorial F sobre uma superfície (isto é, o fluxo da curvatura F ) em três espaços euclidianos à integral de linha do campo vetorial sobre seu limite (também conhecido como integral de loop).

Exemplo de análise vetorial clássica simples

Seja γ : [ a , b ] → R ² uma curva plana de Jordan lisa por partes . O teorema da curva de Jordan implica que γ divide R ² em dois componentes, um compacto e outro não compacto. Seja D a parte compacta que é limitada por γ e suponha que ψ : D → R ³ é suave, com S  : = ψ ( D ) . Se Γ é a curva de espaço definida por Γ ( t ) = ψ ( γ ( t )) e F é um campo vetorial suave em R ³ , então:

${\ displaystyle \ oint _ {\ Gamma} \ mathbf {F} \, \ cdot \, d {\ mathbf {\ Gamma}} = \ iint _ {S} \ nabla \ times \ mathbf {F} \, \ cdot \, d \ mathbf {S}}$

Esta afirmação clássica é um caso especial da formulação geral afirmada acima, após fazer uma identificação do campo vetorial com uma forma 1 e seu enrolamento com uma forma dupla através

${\ displaystyle {\ begin {pmatrix} F_ {x} \\ F_ {y} \\ F_ {z} \\\ end {pmatrix}} \ cdot d \ Gamma \ to F_ {x} \, dx + F_ { y} \, dy + F_ {z} \, dz}$

${\ displaystyle \ nabla \ times {\ begin {pmatrix} F_ {x} \\ F_ {y} \\ F_ {z} \ end {pmatrix}} \ cdot d \ mathbf {S} = {\ begin {pmatrix} \ parcial _ {y} F_ {z} - \ parcial _ {z} F_ {y} \\\ parcial _ {z} F_ {x} - \ parcial _ {x} F_ {z} \\\ parcial _ { x} F_ {y} - \ parcial _ {y} F_ {x} \\\ end {pmatriz}} \ cdot d \ mathbf {S} \ to}$

${\ displaystyle d (F_ {x} \, dx + F_ {y} \, dy + F_ {z} \, dz) = (\ partial _ {y} F_ {z} - \ partial _ {z} F_ { y}) \, dy \ wedge dz + (\ partial _ {z} F_ {x} - \ partial _ {x} F_ {z}) \, dz \ wedge dx + (\ partial _ {x} F_ {y} - \ parcial _ {y} F_ {x}) \, dx \ cunha dy}$.

Outras generalizações clássicas do teorema fundamental do cálculo, como o teorema da divergência e o teorema de Green, são casos especiais da formulação geral declarada acima, após fazer uma identificação padrão de campos vetoriais com formas diferenciais (diferentes para cada um dos teoremas clássicos).

Introdução

O teorema fundamental do cálculo afirma que a integral de uma função f no intervalo [ a , b ] pode ser calculada encontrando uma antiderivada F de  f :

${\ displaystyle \ int _ {a} ^ {b} f (x) \, dx = F (b) -F (a) \,}$

O teorema de Stokes é uma vasta generalização desse teorema no seguinte sentido.

• Pela escolha de F , dF/dx= f ( x ) . No jargão das formas diferenciais , isso significa que f ( x ) dx é a derivada externa da forma 0, ou seja, função, F : em outras palavras, que dF = f dx . Os Stokes gerais teorema se aplica a formas mais elevados diferenciais co , em vez de apenas 0-formas, tais como F .
• Um intervalo fechado [ a , b ] é um exemplo simples de uma variedade unidimensional com limite . Seu limite é o conjunto constituído pelos dois pontos a e b . A integração de f no intervalo pode ser generalizada para a integração de formas em uma variedade de dimensão superior. Duas condições técnicas são necessárias: o coletor deve ser orientável e a forma deve ser compactada para fornecer uma integral bem definida.
• Os dois pontos a e b forma o limite do intervalo fechado. De maneira mais geral, o teorema de Stokes se aplica a variedades orientadas M com limite. O limite ∂ M de H é em si um colector e herda uma orientação natural do que de M . Por exemplo, a orientação natural do intervalo fornece uma orientação dos dois pontos de fronteira. Intuitivamente, a herda a orientação oposta de b , pois eles estão em extremidades opostas do intervalo. Portanto, "integrar" F sobre dois pontos de fronteira a , b é tirar a diferença F ( b ) - F ( a ) .

Em termos ainda mais simples, pode-se considerar os pontos como limites de curvas, ou seja, como limites 0-dimensionais de variedades 1-dimensionais. Assim, assim como se pode encontrar o valor de uma integral ( f dx = dF ) sobre uma variedade unidimensional ( [ a , b ] ), considerando a anti-derivada ( F ) nos limites 0-dimensionais ( { a , b }), pode-se generalizar o teorema fundamental do cálculo, com algumas ressalvas adicionais, para lidar com o valor das integrais ( dω ) sobre variedades n- dimensionais ( Ω ), considerando a antiderivada ( ω ) no ( n - 1 ) limites dimensionais ( ∂Ω ) da variedade.

Portanto, o teorema fundamental diz:

${\ displaystyle \ int _ {[a, b]} f (x) \, dx = \ int _ {[a, b]} \, dF = \ int _ {\ {a \} ^ {-} \ cup \ {b \} ^ {+}} F = F (b) -F (a) \ ,.}$

Formulação para variedades suaves com limite

Deixe Ω ser um orientada variedade suave com limite de dimensão n e deixar α ser um suave n - forma diferencial que é compacta suportado em Ω . Em primeiro lugar, suponha que α seja compactamente suportado no domínio de um gráfico de coordenadas único e orientado { U , φ } . Neste caso, definimos a integral de α sobre Ω como

ou seja, por meio do retrocesso de α para R ⁿ .

De forma mais geral, a integral de α sobre Ω é definida como segue: Seja { ψ _i } uma partição de unidade associada a uma cobertura localmente finita { U _i , φ _i } de gráficos de coordenadas (orientados de forma consistente), então defina a integral

onde cada termo na soma é avaliado puxando de volta para R ⁿ como descrito acima. Essa quantidade está bem definida; ou seja, não depende da escolha das cartas de coordenadas, nem da partição da unidade.

O teorema de Stokes generalizado lê:

Convencionalmente, é abreviado como , uma vez que a retirada de uma forma diferencial pela inclusão mapa é simplesmente a sua restrição ao seu domínio: . Aqui está a derivada externa , que é definida usando apenas a estrutura múltipla. O lado direito às vezes é escrito para enfatizar o fato de que a -variedade não tem limite. (Este fato também é uma implicação do teorema de Stokes, uma vez que para uma dada variedade de dimensão suave , a aplicação do teorema duas vezes dá para qualquer forma , o que implica isso .) O lado direito da equação é freqüentemente usado para formular leis integrais ; o lado esquerdo leva então a formulações diferenciais equivalentes (veja abaixo). ${\ textstyle \ int _ {\ partial \ Omega} i ^ {*} \ omega}$${\ textstyle \ int _ {\ partial \ Omega} \ omega}$${\ displaystyle i ^ {*} \ omega = \ omega | _ {\ partial \ Omega}}$${\ displaystyle d}$${\ textstyle \ oint _ {\ partial \ Omega} \ omega}$${\ displaystyle (n-1)}$${\ displaystyle \ partial \ Omega}$${\ displaystyle n}$${\ displaystyle \ Omega}$${\ textstyle \ int _ {\ partial (\ partial \ Omega)} \ omega = \ int _ {\ Omega} d (d \ omega) = 0}$${\ displaystyle (n-2)}$${\ displaystyle \ omega}$${\ displaystyle \ partial (\ partial \ Omega) = \ emptyset}$

O teorema é freqüentemente usado em situações onde está uma subvariedade orientada embutida de alguma variedade maior, frequentemente , na qual a forma é definida. ${\ displaystyle \ Omega}$${\ displaystyle \ mathbf {R} ^ {k}}$${\ displaystyle \ omega}$

Preliminares topológicos; integração sobre cadeias

Seja M uma variedade lisa . Um (liso) singular k -simplex em H é definido como um mapa liso do simplex padrão em R ^k para M . O grupo C _K ( H , Z ) de singular k - cadeias em M é definido como sendo o grupo abeliano livre sobre o conjunto de singulares k -simplices em H . Esses grupos, junto com o mapa de fronteira, ∂ , definem um complexo de cadeia . O grupo correspondente homologia (resp. Cohomología) é isomorfa a habitual singular homologia grupo H _k ( M , Z ) (resp. O singular cohomología grupo H ^k ( M , Z ) ), definido utilizando contínua em vez de simplices lisas em H .

Por outro lado, as formas diferenciais, com derivada externa, d , como o mapa de conexão, formam um complexo de cochain, que define os grupos de cohomologia de de Rham H^k
_dR( M , R ) .

As k- formas diferenciais podem ser integradas em um k -simplex de uma maneira natural, puxando de volta para R ^k . A extensão por linearidade permite a integração em cadeias. Isso dá um mapa linear do espaço de k- formas para o k- ésimo grupo de cochains singulares, C ^k ( M , Z ) , os funcionais lineares em C _k ( M , Z ) . Em outras palavras, uma forma k ω define uma forma funcional

nas k -chains. O teorema de Stokes diz que este é um mapa de cadeia da cohomologia de de Rham para a cohomologia singular com coeficientes reais; a derivada externa, d , se comporta como o dual de ∂ nas formas. Isso dá um homomorfismo da cohomologia de de Rham para a cohomologia singular. No nível dos formulários, isso significa:

1. formas fechadas, ou seja, dω = 0 , têm integral zero sobre os limites , ou seja, sobre variedades que podem ser escritas como ∂Σ _c M _c , e
2. formas exatas, ou seja, ω = dσ , têm integral zero ao longo dos ciclos , ou seja, se a soma dos limites for o conjunto vazio: Σ _c M _c = ∅ .

O teorema de De Rham mostra que esse homomorfismo é na verdade um isomorfismo . Portanto, o inverso de 1 e 2 acima é verdadeiro. Em outras palavras, se { c _i } são ciclos gerando o k- ésimo grupo de homologia, então para quaisquer números reais correspondentes, { a _i } , existe uma forma fechada, ω , tal que

e este formulário é exclusivo até as formas exatas.

O teorema de Stokes sobre variedades suaves pode ser derivado do teorema de Stokes para cadeias em variedades suaves e vice-versa. Declarado formalmente, o último diz:

Princípio subjacente

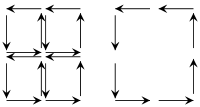
Para simplificar esses argumentos topológicos, vale a pena examinar o princípio subjacente considerando um exemplo para d = 2 dimensões. A ideia essencial pode ser compreendida pelo diagrama à esquerda, que mostra que, em uma telha orientada de um manifold, os caminhos internos são percorridos em direções opostas; suas contribuições para a integral do caminho, portanto, se cancelam entre pares. Como consequência, apenas a contribuição da fronteira permanece. Portanto, é suficiente provar o teorema de Stokes para coisas suficientemente finas (ou, equivalentemente, simplicos ), o que geralmente não é difícil.

Generalização para conjuntos aproximados

A formulação acima, na qual Ω é uma variedade suave com limite, não é suficiente em muitas aplicações. Por exemplo, se o domínio de integração é definido como a região plana entre duas coordenadas x e os gráficos de duas funções, frequentemente acontecerá que o domínio tenha cantos. Nesse caso, os pontos de canto significam que Ω não é uma variedade suave com limite e, portanto, a afirmação do teorema de Stokes dada acima não se aplica. No entanto, é possível verificar que a conclusão do teorema de Stokes ainda é verdadeira. Isso ocorre porque Ω e seu limite são bem comportados longe de um pequeno conjunto de pontos (um conjunto de medida zero ).

Uma versão do teorema de Stokes que permite aspereza foi provada por Whitney. Suponha que D seja um subconjunto aberto limitado conectado de R ⁿ . Chamada D um domínio padrão , desde que preencha as seguintes propriedades: Existe um subconjunto P de ∂ D , aberto em ∂ D , cujo complemento em ∂ D tem Hausdorff ( n - 1) -measure zero; e de modo que todo ponto de P tem um vetor normal generalizado . Este é um vetor v ( x ) tal que, se um sistema de coordenadas for escolhido de forma que v ( x ) seja o primeiro vetor de base, então, em uma vizinhança aberta em torno de x , existe uma função suave f ( x ₂ , .. ., x _n ) de modo que P é o gráfico { x ₁ = f ( x ₂ , ..., x _n )} e D é a região { x ₁  : x ₁ < f ( x ₂ , ..., x _n )} . Whitney observa que o limite de um domínio padrão é a união de um conjunto de zero Hausdorff ( n - 1) -medida e uma união finita ou contável de ( n - 1) -variedades suaves, cada uma das quais tem o domínio em apenas uma lado. Ele então prova que se D é um domínio padrão em R ⁿ , ω é uma ( n - 1) forma que é definida, contínua e limitada em D ∪ P , suave em D , integrável em P , e tal que dω é integrável em D , então o teorema de Stokes é válido, isto é,

${\ displaystyle \ int _ {P} \ omega = \ int _ {D} d \ omega \ ,.}$

O estudo das propriedades teóricas da medida de conjuntos brutos leva à teoria da medida geométrica . Versões ainda mais gerais do teorema de Stokes foram provadas por Federer e por Harrison.

Casos especiais

A forma geral do teorema de Stokes usando formas diferenciais é mais poderosa e mais fácil de usar do que os casos especiais. As versões tradicionais podem ser formuladas usando coordenadas cartesianas sem o maquinário da geometria diferencial e, portanto, são mais acessíveis. Além disso, eles são mais velhos e, como resultado, seus nomes são mais familiares. As formas tradicionais são frequentemente consideradas mais convenientes pelos cientistas e engenheiros praticantes, mas a não naturalidade da formulação tradicional torna-se aparente ao usar outros sistemas de coordenadas, mesmo os familiares, como coordenadas esféricas ou cilíndricas. Há potencial para confusão na forma como os nomes são aplicados e no uso de formulações duais.

Teorema de Kelvin-Stokes

Este é um caso (dualizado) (1 + 1) -dimensional, para uma forma 1 (dualizado porque é uma declaração sobre campos vetoriais ). Este caso especial é frequentemente referido apenas como teorema de Stokes em muitos cursos introdutórios de cálculo vetorial na universidade e é usado em física e engenharia. Às vezes também é conhecido como teorema do curl .

O teorema de Kelvin-Stokes clássico relaciona a integral de superfície da curvatura de um campo vetorial sobre uma superfície Σ em três espaços euclidianos à integral de linha do campo vetorial sobre seu limite. É um caso especial do teorema geral de Stokes (com n = 2 ), uma vez que identificamos um campo vetorial com uma forma 1 usando a métrica no espaço 3 euclidiano. A curva da integral da linha, ∂Σ , deve ter orientação positiva , o que significa que ∂Σ aponta no sentido anti-horário quando a normal da superfície , n , aponta para o observador.

Uma consequência do teorema de Kelvin-Stokes é que as linhas de campo de um campo vetorial com curvatura zero não podem ser contornos fechados. A fórmula pode ser reescrita como:

Teorema de Green

O teorema de Green é imediatamente reconhecível como o terceiro integrando de ambos os lados na integral em termos de P , Q e R citados acima.

No eletromagnetismo

Duas das quatro equações de Maxwell envolvem curvas de campos vetoriais 3-D, e suas formas diferencial e integral são relacionadas pelo teorema de Kelvin-Stokes . Deve-se ter cuidado para evitar casos com limites móveis: as derivadas de tempo parcial têm como objetivo excluir tais casos. Se os limites móveis forem incluídos, o intercâmbio de integração e diferenciação introduzirá termos relacionados ao movimento do limite não incluídos nos resultados abaixo (consulte Diferenciação sob o sinal integral ):

Nome	Forma diferencial	Forma integral (usando o teorema de Kelvin-Stokes mais invariância relativística, ∫∂/∂ t ... → d/dt∫ ... )
Equação de Maxwell-Faraday Lei de indução de Faraday :	${\ displaystyle \ quad \ nabla \ times \ mathbf {E} = - {\ frac {\ partial \ mathbf {B}} {\ partial t}} \ quad}$	${\ displaystyle {\ begin {alinhados} \ quad \ oint _ {C} \ mathbf {E} \ cdot d \ mathbf {l} & = \ iint _ {S} \ nabla \ times \ mathbf {E} \ cdot d \ mathbf {A} \\ & = - \ iint _ {S} {\ frac {\ partial \ mathbf {B}} {\ partial t}} \ cdot d \ mathbf {A} \ end {alinhados}} \ quad }$(com C e S não necessariamente estacionário)
Lei de Ampère (com extensão de Maxwell):	${\ displaystyle \ quad \ nabla \ times \ mathbf {H} = \ mathbf {J} + {\ frac {\ partial \ mathbf {D}} {\ partial t}} \ quad}$	${\ displaystyle {\ begin {alinhados} \ quad \ oint _ {C} \ mathbf {H} \ cdot d \ mathbf {l} & = \ iint _ {S} \ nabla \ times \ mathbf {H} \ cdot d \ mathbf {A} \\ & = \ iint _ {S} \ mathbf {J} \ cdot d \ mathbf {A} + \ iint _ {S} {\ frac {\ partial \ mathbf {D}} {\ partial t}} \ cdot d \ mathbf {A} \ end {alinhado}} \ quad}$(com C e S não necessariamente estacionário)

O subconjunto listado acima das equações de Maxwell é válido para campos eletromagnéticos expressos em unidades SI . Em outros sistemas de unidades, como unidades CGS ou Gaussianas , os fatores de escala para os termos são diferentes. Por exemplo, em unidades gaussianas, a lei da indução de Faraday e a lei de Ampère assumem as formas:

${\ displaystyle {\ begin {alinhados} \ nabla \ times \ mathbf {E} & = - {\ frac {1} {c}} {\ frac {\ partial \ mathbf {B}} {\ partial t}} \ ,, \\\ nabla \ times \ mathbf {H} & = {\ frac {1} {c}} {\ frac {\ partial \ mathbf {D}} {\ partial t}} + {\ frac {4 \ pi} {c}} \ mathbf {J} \ ,, \ end {alinhado}}}$

respectivamente, onde c é a velocidade da luz no vácuo.

Teorema da divergência

Da mesma forma, o teorema da divergência

${\ displaystyle \ int _ {\ mathrm {Vol}} \ nabla \ cdot \ mathbf {F} \, d _ {\ mathrm {Vol}} = \ oint _ {\ partial \ operatorname {Vol}} \ mathbf {F} \ cdot d {\ boldsymbol {\ Sigma}}}$

é um caso especial se identificarmos um campo vetorial com a forma ( n - 1) obtida pela contração do campo vetorial com a forma de volume euclidiano. Uma aplicação disso é o caso F = f c, onde c é um vetor constante arbitrário. Trabalhar a divergência do produto dá

${\ displaystyle \ mathbf {c} \ cdot \ int _ {\ mathrm {Vol}} \ nabla f \, d _ {\ mathrm {Vol}} = \ mathbf {c} \ cdot \ oint _ {\ partial \ mathrm { Vol}} f \, d {\ boldsymbol {\ Sigma}} \,}$

Uma vez que isso vale para todos os c que encontramos

${\ displaystyle \ int _ {\ mathrm {Vol}} \ nabla f \, d _ {\ mathrm {Vol}} = \ oint _ {\ partial \ mathrm {Vol}} f \, d {\ boldsymbol {\ Sigma} } \ ,.}$

Veja também

• Lema Chandrasekhar – Wentzel

Notas de rodapé

Referências

Leitura adicional

• Grunsky, Helmut (1983). O Teorema de General Stokes . Boston: Pitman. ISBN 0-273-08510-7.
• Katz, Victor J. (maio de 1979). "The History of Stokes 'Theorem". Revista Matemática . 52 (3): 146–156. doi : 10.2307 / 2690275 . JSTOR  2690275 .
• Loomis, Lynn Harold ; Sternberg, Shlomo (2014). Cálculo avançado . Hackensack, New Jersey: World Scientific. ISBN 978-981-4583-93-0.
• Madsen, Ib ; Tornehave, Jørgen (1997). Do Cálculo à Cohomologia: Cohomologia de De Rham e classes características . Cambridge, Reino Unido: Cambridge University Press. ISBN 0-521-58956-8.
• Marsden, Jerrold E .; Anthony, Tromba (2003). Vector Calculus (5ª ed.). W. H. Freeman.
• Lee, John (2003). Introdução aos distribuidores suaves . Springer-Verlag. ISBN 978-0-387-95448-6.
• Rudin, Walter (1976). Princípios de Análise Matemática . Nova York, NY: McGraw – Hill. ISBN 0-07-054235-X.
• Spivak, Michael (1965). Cálculo em variedades: uma abordagem moderna aos teoremas clássicos de cálculo avançado . São Francisco: Benjamin Cummings. ISBN 0-8053-9021-9.
• Stewart, James (2009). Cálculo: conceitos e contextos . Cengage Learning. pp. 960–967. ISBN 978-0-495-55742-5.
• Stewart, James (2003). Cálculo: Primeiras Funções Transcendentais (5ª ed.). Brooks / Cole.
• Tu, Loring W. (2011). Uma Introdução aos Manifolds (2ª ed.). Nova York: Springer. ISBN 978-1-4419-7399-3.

links externos

• Mídia relacionada ao teorema de Stokes no Wikimedia Commons
• "Stokes formula" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Prova do Teorema da Divergência e do Teorema de Stokes
• Cálculo 3 - Teorema de Stokes de lamar.edu - uma explicação expositiva
• "Teorema de Stokes sobre variedades" . Aleph Zero . 3 de maio de 2020 - via YouTube .