Espaço de coordenadas reais - Real coordinate space

A estrutura cartesiana do produto de R ² no plano cartesiano de pares ordenados ( x ,  y ) . Linhas azuis denotam eixos de coordenadas , linhas verdes horizontais são inteiros y , linhas ciano verticais são inteiros x , linhas marrom-laranja mostram meio-inteiro x ou y , magenta e sua tonalidade mostram múltiplos de um décimo (melhor visto sob ampliação)

Em matemática , uma coordenada real espaço de dimensão N , escrito R ⁿ ( / ɑr ɛ n / ar- EN ) ou , é um espaço de coordenadas sobre os números reais . Isso significa que é o conjunto das n -tuplas de números reais (sequências de n números reais). Com adição de componentes e multiplicação escalar, é um espaço vetorial real . ${\ displaystyle \ mathbb {R} ^ {n}}$

Normalmente, as coordenadas cartesianas dos elementos de um espaço euclidiano formam um espaço de coordenadas real. Isso explica o nome do espaço de coordenadas e o fato de que termos geométricos são freqüentemente usados ​​ao trabalhar com espaços de coordenadas. Por exemplo, R ² é um plano .

Espaços de coordenadas são amplamente utilizados em geometria e física , pois seus elementos permitem localizar pontos em espaços euclidianos e computar com eles.

Definição e estruturas

Para qualquer número natural n , o conjunto R ⁿ consiste em todas as n - tuplas de números reais ( R ). É chamado de " espaço real n- dimensional" ou " espaço n- real ".

Um elemento de R ⁿ é, portanto, um n- duplo, e é escrito

${\ displaystyle (x_ {1}, x_ {2}, \ ldots, x_ {n})}$

onde cada x _i é um número real. Assim, no cálculo multivariável , o domínio de uma função de várias variáveis ​​reais e o codomínio de uma função de valor vetorial real são subconjuntos de R ⁿ para algum n .

O espaço n real tem várias propriedades adicionais, notavelmente:

• Com adição de componentes e multiplicação escalar , é um espaço vetorial real . Todo espaço vetorial real n- dimensional é isomórfico a ele.
• Com o produto escalar (soma do produto termo por termo dos componentes), é um espaço de produto interno . Cada espaço de produto interno real n- dimensional é isomórfico a ele.
• Como todo espaço de produto interno, é um espaço topológico e um espaço vetorial topológico .
• É um espaço euclidiano e um espaço real afim , e todo espaço euclidiano ou afim é isomórfico a ele.
• É uma variedade analítica e pode ser considerada o protótipo de todas as variedades , pois, por definição, uma variedade é, perto de cada ponto, isomórfica a um subconjunto aberto de R ⁿ .
• É uma variedade algébrica e toda variedade algébrica real é um subconjunto de R ⁿ .

Essas propriedades e estruturas de R ^{n o} tornam fundamental em quase todas as áreas da matemática e seus domínios de aplicação, como estatística , teoria da probabilidade e muitas partes da física .

O domínio de uma função de várias variáveis

Qualquer função f ( x ₁ ,  x ₂ ,…,  x _n ) de n variáveis ​​reais pode ser considerada como uma função em R ⁿ (ou seja, com R ⁿ como seu domínio ). O uso do espaço n real , em vez de várias variáveis ​​consideradas separadamente, pode simplificar a notação e sugerir definições razoáveis. Considere, para n = 2 , uma composição de função da seguinte forma:

${\ displaystyle F (t) = f (g_ {1} (t), g_ {2} (t)),}$

onde as funções g ₁ e g ₂ são contínuas . Se

∀ x ₁  ∈  R  : f ( x ₁ , ·) é contínuo (por x ₂ )

∀ x ₂  ∈  R  : f (·,  x ₂ ) é contínuo (por x ₁ )

então F não é necessariamente contínuo. A continuidade é uma condição mais forte: a continuidade de f no natural R ² topologia ( discutido abaixo ), também chamado continuidade multivariada , que é suficiente para a continuidade da composição F .

Espaço vetorial

O espaço de coordenadas R ⁿ forma um espaço vetorial n- dimensional sobre o campo de números reais com a adição da estrutura de linearidade , e freqüentemente ainda é denotado por R ⁿ . As operações em R ⁿ como um espaço vetorial são tipicamente definidas por

${\ displaystyle \ mathbf {x} + \ mathbf {y} = (x_ {1} + y_ {1}, x_ {2} + y_ {2}, \ ldots, x_ {n} + y_ {n})}$

${\ displaystyle \ alpha \ mathbf {x} = (\ alpha x_ {1}, \ alpha x_ {2}, \ ldots, \ alpha x_ {n}).}$

O vetor zero é dado por

${\ displaystyle \ mathbf {0} = (0,0, \ ldots, 0)}$

e o inverso aditivo do vetor x é dado por

${\ displaystyle - \ mathbf {x} = (- x_ {1}, - x_ {2}, \ ldots, -x_ {n}).}$

Esta estrutura é importante porque qualquer espaço vetorial real n- dimensional é isomórfico ao espaço vetorial R ⁿ .

Notação de matriz

Na notação de matriz padrão , cada elemento de R ⁿ é normalmente escrito como um vetor de coluna

${\ displaystyle \ mathbf {x} = {\ begin {bmatrix} x_ {1} \\ x_ {2} \\\ vdots \\ x_ {n} \ end {bmatrix}}}$

e às vezes como um vetor linha :

${\ displaystyle \ mathbf {x} = {\ begin {bmatrix} x_ {1} & x_ {2} & \ cdots & x_ {n} \ end {bmatrix}}.}$

O espaço de coordenadas R ⁿ pode então ser interpretado como o espaço de todos os vetores de coluna n  × 1 , ou todos os vetores de linha 1 ×  n com as operações matriciais ordinárias de adição e multiplicação escalar .

As transformações lineares de R ⁿ em R ^m podem então ser escritas como matrizes m  ×  n que atuam nos elementos de R ⁿ através da multiplicação à esquerda (quando os elementos de R ⁿ são vetores de coluna) e nos elementos de R ^m através da multiplicação à direita (quando eles são vetores de linha). A fórmula para multiplicação à esquerda, um caso especial de multiplicação de matrizes , é:

${\ displaystyle (A {\ mathbf {x}}) _ {k} = \ sum \ limits _ {l = 1} ^ {n} A_ {kl} x_ {l}}$

Qualquer transformação linear é uma função contínua (veja abaixo ). Além disso, uma matriz define um mapa aberto de R ⁿ a R ^m se e somente se a classificação da matriz for igual a m .

Base padrão

O espaço de coordenadas R ⁿ vem com uma base padrão:

${\ displaystyle {\ begin {alinhados} \ mathbf {e} _ {1} & = (1,0, \ ldots, 0) \\\ mathbf {e} _ {2} & = (0,1, \ ldots , 0) \\ & {} \; \; \ vdots \\\ mathbf {e} _ {n} & = (0,0, \ ldots, 1) \ end {alinhado}}}$

Para ver que esta é uma base, observe que um vetor arbitrário em R ⁿ pode ser escrito exclusivamente na forma

${\ displaystyle \ mathbf {x} = \ sum _ {i = 1} ^ {n} x_ {i} \ mathbf {e} _ {i}.}$

Propriedades geométricas e usos

Orientação

O fato de que os números reais , ao contrário de muitos outros campos , constituem um campo ordenado produz uma estrutura de orientação em R ⁿ . Qualquer mapa linear completo de R ⁿ para si mesmo preserva ou inverte a orientação do espaço dependendo do sinal do determinante de sua matriz. Se alguém permutar coordenadas (ou, em outras palavras, elementos da base), a orientação resultante dependerá da paridade da permutação .

Os difeomorfismos de R ⁿ ou domínios nele , por sua virtude de evitar zero Jacobiano , também são classificados em preservação de orientação e reversão de orientação. Tem consequências importantes para a teoria das formas diferenciais , cujas aplicações incluem a eletrodinâmica .

Outra manifestação dessa estrutura é que o ponto de reflexão em R ⁿ tem propriedades diferentes dependendo da uniformidade de n . Para n ímpar, ele preserva a orientação, enquanto para n ímpar é invertido (consulte também rotação inadequada ).

Espaço afim

R ⁿ entendido como um espaço afim é o mesmo espaço, onde R ⁿ como um espaço vetorial atua por translações . Por outro lado, um vetor deve ser entendido como uma " diferença entre dois pontos", geralmente ilustrada por um segmento de linha direcionado conectando dois pontos. A distinção diz que não há escolha canônica de onde a origem deve ir em um n- espaço afim , porque ela pode ser traduzida em qualquer lugar.

Convexidade

O n -simplex (veja abaixo ) é o conjunto convexo padrão, que mapeia para cada politopo, e é a interseção do hiperplano afim padrão ( n + 1) (espaço afim padrão) e o padrão ( n + 1) orthant (padrão cone).

Em um espaço vetorial real, como R ⁿ , pode-se definir um cone convexo , que contém todas as combinações lineares não negativas de seus vetores. O conceito correspondente em um espaço afim é um conjunto convexo , que permite apenas combinações convexas (combinações lineares não negativas que somam 1).

Na linguagem da álgebra universal , um espaço vetorial é uma álgebra sobre o espaço vetorial universal R ^∞ de sequências finitas de coeficientes, correspondendo a somas finitas de vetores, enquanto um espaço afim é uma álgebra sobre o hiperplano afim universal neste espaço (de sequências finitas que somam 1), um cone é uma álgebra sobre o orthant universal (de sequências finitas de números não negativos) e um conjunto convexo é uma álgebra sobre o simplex universal (de sequências finitas de números não negativos que somam 1). Isso geometriza os axiomas em termos de "somas com (possíveis) restrições nas coordenadas".

Outro conceito da análise convexa é uma função convexa de R ⁿ para números reais, que é definida por meio de uma desigualdade entre seu valor em uma combinação convexa de pontos e a soma dos valores nesses pontos com os mesmos coeficientes.

Espaço euclidiano

O produto escalar

${\ displaystyle \ mathbf {x} \ cdot \ mathbf {y} = \ sum _ {i = 1} ^ {n} x_ {i} y_ {i} = x_ {1} y_ {1} + x_ {2} y_ {2} + \ cdots + x_ {n} y_ {n}}$

define a norma | x | = √ x ⋅ x no espaço vetorial R ⁿ . Se cada vetor tem sua norma euclidiana , então para qualquer par de pontos a distância

${\ displaystyle d (\ mathbf {x}, \ mathbf {y}) = \ | \ mathbf {x} - \ mathbf {y} \ | = {\ sqrt {\ sum _ {i = 1} ^ {n} (x_ {i} -y_ {i}) ^ {2}}}}$

é definido, fornecendo uma estrutura de espaço métrico em R ⁿ além de sua estrutura afim.

Quanto à estrutura do espaço vetorial, o produto escalar e a distância euclidiana geralmente são assumidos como existindo em R ⁿ sem explicações especiais. No entanto, o espaço n real e um espaço n euclidiano são objetos distintos, estritamente falando. Qualquer espaço n euclidiano tem um sistema de coordenadas onde o produto escalar e a distância euclidiana têm a forma mostrada acima, chamada cartesiana . Mas existem muitos sistemas de coordenadas cartesianas em um espaço euclidiano.

Por outro lado, a fórmula acima para a métrica euclidiana define a estrutura euclidiana padrão em R ⁿ , mas não é a única possível. Na verdade, qualquer forma quadrática definida positiva q define sua própria "distância" √ q ( x - y ) , mas não é muito diferente da euclidiana no sentido de que

${\ displaystyle \ exists C_ {1}> 0, \ \ exists C_ {2}> 0, \ \ forall \ mathbf {x}, \ mathbf {y} \ in \ mathbb {R} ^ {n}: C_ { 1} d (\ mathbf {x}, \ mathbf {y}) \ leq {\ sqrt {q (\ mathbf {x} - \ mathbf {y})}} \ leq C_ {2} d (\ mathbf {x }, \ mathbf {y}).}$

Essa mudança da métrica preserva algumas de suas propriedades, por exemplo, a propriedade de ser um espaço métrico completo . Isso também implica que qualquer transformação linear completa de R ⁿ , ou sua transformação afim , não aumenta as distâncias mais do que por algum C ₂ fixo e não torna as distâncias menores do que 1 ∕  C ₁ vezes, um número finito fixo vezes menor .

A equivalência acima mencionada de funções métricas permanece válida se √ q ( x - y ) for substituído por M ( x - y ) , onde M é qualquer função homogênea convexa positiva de grau 1, ou seja, uma norma vetorial (ver distância de Minkowski para exemplos úteis) . Devido ao fato de que qualquer métrica "natural" em R ⁿ não é especialmente diferente da métrica euclidiana, R ⁿ nem sempre se distingue de um n- espaço euclidiano, mesmo em trabalhos matemáticos profissionais.

Em geometria algébrica e diferencial

Embora a definição de uma variedade não exija que seu espaço de modelo seja R ⁿ , esta escolha é a mais comum e quase exclusiva em geometria diferencial .

Por outro lado, os teoremas de incorporação de Whitney afirmam que qualquer variedade real diferenciável m- dimensional pode ser incorporada em R ^{2 m} .

Outras aparições

Outras estruturas consideradas em R ⁿ incluem a de um espaço pseudo-euclidiano , a estrutura simplética ( n par ) e a estrutura de contato ( n ímpar ). Todas essas estruturas, embora possam ser definidas de forma livre de coordenadas, admitem formas padrão (e razoavelmente simples) em coordenadas.

R ⁿ é também um subespaço vetorial real de C ⁿ que é invariante à conjugação complexa ; veja também complexificação .

Polopos em R ⁿ

Existem três famílias de politopos que têm representações simples em espaços R ⁿ , para qualquer n , e podem ser usados ​​para visualizar qualquer sistema de coordenadas afins em um espaço n real . Os vértices de um hipercubo têm coordenadas ( x ₁ ,  x ₂ , ...,  x _n ) onde cada x _k assume um de apenas dois valores, normalmente 0 ou 1. No entanto, quaisquer dois números podem ser escolhidos em vez de 0 e 1, para exemplo -1 e 1. Um n- hipercubo pode ser pensado como o produto cartesiano de n intervalos idênticos (como o intervalo de unidade [0,1] ) na linha real. Como um subconjunto n- dimensional, pode ser descrito com um sistema de 2 n desigualdades :

${\ displaystyle \ displaystyle {\ begin {matrix} 0 \ leq x_ {1} \ leq 1 \\\ vdots \\ 0 \ leq x_ {n} \ leq 1 \ end {matrix}}}$ (para [0,1] )

${\ displaystyle \ displaystyle {\ begin {matrix} | x_ {1} | \ leq 1 \\\ vdots \\ | x_ {n} | \ leq 1 \ end {matrix}}}$ (para [-1,1] )

Cada vértice da cruz-poliepítopo tem, para alguns k , a x _k coordenar igual a ± 1 e todas as outras coordenadas igual a 0 (de modo a que ele é o k th vetor base padrão até sinal ). Este é um politopo duplo de hipercubo. Como um subconjunto n- dimensional, pode ser descrito com uma única desigualdade que usa a operação de valor absoluto :

${\ displaystyle \ sum \ limits _ {k = 1} ^ {n} | x_ {k} | \ leq 1 \ ,,}$

mas isso também pode ser expresso com um sistema de 2 ⁿ desigualdades lineares.

O terceiro politopo com coordenadas simplesmente enumeráveis ​​é o simplex padrão , cujos vértices são n vetores de base padrão e a origem (0, 0, ..., 0) . Como um subconjunto n- dimensional, é descrito com um sistema de n + 1 desigualdades lineares:

${\ displaystyle {\ begin {matrix} 0 \ leq x_ {1} \\\ vdots \\ 0 \ leq x_ {n} \\\ sum \ limits _ {k = 1} ^ {n} x_ {k} \ leq 1 \ end {matriz}}}$

A substituição de todos os "≤" por "<" fornece os interiores desses politopos.

Propriedades topológicas

A estrutura topológica de R ⁿ (chamada de topologia padrão , topologia euclidiana ou topologia usual ) pode ser obtida não apenas do produto cartesiano . Também é idêntica à topologia natural induzida pela métrica euclidiana discutida acima : um conjunto é aberto na topologia euclidiana se e somente se contém uma bola aberta ao redor de cada um de seus pontos. Além disso, R ⁿ é um espaço topológico linear (veja continuidade de mapas lineares acima), e há apenas uma topologia possível (não trivial) compatível com sua estrutura linear. Como existem muitos mapas lineares abertos de R ⁿ para si mesmo que não são isometrias , pode haver muitas estruturas euclidianas em R ⁿ que correspondem à mesma topologia. Na verdade, não depende muito nem mesmo da estrutura linear: existem muitos difeomorfismos não lineares (e outros homeomorfismos) de R ⁿ sobre si mesmo, ou de suas partes, como uma bola aberta euclidiana ou o interior de um hipercubo ).

R ⁿ tem a dimensão topológica n . Um resultado importante na topologia de R ⁿ , que está longe de ser superficial, é a invariância de domínio de Brouwer . Qualquer subconjunto de R ⁿ (com sua topologia de subespaço ) que seja homeomórfico a outro subconjunto aberto de R ⁿ é ele próprio aberto. Uma consequência imediata disso é que R ^m não é homeomórfico a R ⁿ se m ≠ n - um resultado intuitivamente "óbvio" que, no entanto, é difícil de provar.

Apesar da diferença na dimensão topológica, e ao contrário de uma percepção ingênua, é possível mapear um espaço real de menor dimensão contínua e sobrejetivamente em R ⁿ . Uma curva de preenchimento de espaço contínua (embora não suave) (uma imagem de R ¹ ) é possível.

Exemplos

Vetor de coluna vazia , o único elemento de R 0

R 1

n ≤ 1

Casos de 0 ≤ n ≤ 1 não oferecem nada de novo: R ¹ é a reta real , enquanto R ⁰ (o espaço contendo o vetor coluna vazio) é um singleton , entendido como um espaço vetorial zero . No entanto, é útil incluí-los como casos triviais de teorias que descrevem n diferentes .

n = 2

Tanto o hipercubo quanto o politopo cruzado em R ² são quadrados , mas as coordenadas dos vértices são organizadas de forma diferente

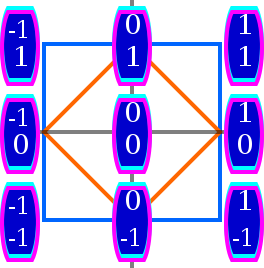
n = 3

O cubo (o hipercubo) e o octaedro (o politopo cruzado) de R ³ . Coordenadas não são mostradas

n = 4

R ⁴ pode ser imaginado usando o fato de que 16 pontos ( x ₁ ,  x ₂ ,  x ₃ ,  x ₄ ) , onde cada x _k é 0 ou 1, são vértices de um tesserato (na foto), o 4-hipercubo (ver acima ).

O primeiro uso principal de R ⁴ é um modelo de espaço - tempo : três coordenadas espaciais mais uma temporal . Isso geralmente está associado à teoria da relatividade , embora quatro dimensões tenham sido usadas para tais modelos desde Galileu . A escolha da teoria leva a uma estrutura diferente, porém: na relatividade galileana a coordenada t é privilegiada, mas na relatividade einsteiniana não. A relatividade especial se passa no espaço de Minkowski . A relatividade geral usa espaços curvos, que podem ser considerados como R ⁴ com uma métrica curva para a maioria dos propósitos práticos. Nenhuma dessas estruturas fornece uma métrica (definida positiva) em R ⁴ .

Euclidiano R ⁴ também atrai a atenção de matemáticos, por exemplo, devido à sua relação com quaternions , um 4-dimensional álgebra reais si. Consulte as rotações no espaço euclidiano de 4 dimensões para obter algumas informações.

Na geometria diferencial, n = 4 é o único caso em que R ⁿ admite uma estrutura diferencial não padronizada : ver R ⁴ exótico .

Normas em R ⁿ

Pode-se definir muitas normas no espaço vetorial R ⁿ . Alguns exemplos comuns são

• a norma p , definida por for all, onde é um número inteiro positivo. O caso é muito importante, porque é exatamente a norma euclidiana . ${\ textstyle \ | \ mathbf {x} \ | _ {p}: = {\ sqrt [{p}] {\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {p}} }}$${\ displaystyle \ mathbf {x} \ in \ mathbb {R} ^ {n}}$${\ displaystyle p}$${\ displaystyle p = 2}$
• a norma ou norma máxima , definida por para todos os R ⁿ . Este é o limite de todos os p-normas : . ${\ displaystyle \ infty}$${\ displaystyle \ | \ mathbf {x} \ | _ {\ infty}: = \ max \ {x_ {1}, \ dots, x_ {n} \}}$${\ displaystyle {\ textbf {x}} \ in}$ ${\ textstyle \ | \ mathbf {x} \ | _ {\ infty} = \ lim _ {p \ to \ infty} {\ sqrt [{p}] {\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {p}}}}$

Um resultado realmente surpreendente e útil é que todas as normas definidas em R ⁿ são equivalentes . Isso significa que para duas normas arbitrárias e em R ⁿ você sempre pode encontrar números reais positivos , de modo que ${\ displaystyle \ | \ cdot \ |}$${\ displaystyle \ | \ cdot \ | '}$${\ displaystyle \ alpha, \ beta> 0}$

${\ displaystyle \ alpha \ cdot \ | \ mathbf {x} \ | \ leq \ | \ mathbf {x} \ | '\ leq \ beta \ cdot \ | \ mathbf {x} \ |}$ para todos . ${\ displaystyle {\ textbf {x}} \ in \ mathbb {R} ^ {n}}$

Isso define uma relação de equivalência no conjunto de todas as normas em R ⁿ . Com este resultado, você pode verificar se uma sequência de vetores em R ⁿ converge com se e somente se converge com . ${\ displaystyle \ | \ cdot \ |}$${\ displaystyle \ | \ cdot \ | '}$

Aqui está um esboço de como pode ser uma prova desse resultado:

Por causa da relação de equivalência , é suficiente mostrar que toda norma em R ⁿ é equivalente à norma euclidiana . Deixe ser uma norma arbitrária em R ⁿ . A prova é dividida em duas etapas: ${\ displaystyle \ | \ cdot \ | _ {2}}$${\ displaystyle \ | \ cdot \ |}$

• Mostramos que existe um , tal que para todos . Nesta etapa, você usar o fato de que cada pode ser representado como uma combinação linear do padrão base : . Então, com a desigualdade de Cauchy-Schwarz , onde . ${\ displaystyle \ beta> 0}$${\ displaystyle \ | \ mathbf {x} \ | \ leq \ beta \ cdot \ | \ mathbf {x} \ | _ {2}}$${\ displaystyle {\ textbf {x}} \ in \ mathbb {R} ^ {n}}$${\ displaystyle {\ textbf {x}} = (x_ {1}, \ dots, x_ {n}) \ in \ mathbb {R} ^ {n}}$${\ textstyle \ mathbf {x} = \ sum _ {i = 1} ^ {n} e_ {i} \ cdot x_ {i}}$ ${\ displaystyle \ | \ mathbf {x} \ | = \ left \ | \ sum _ {i = 1} ^ {n} e_ {i} \ cdot x_ {i} \ right \ | \ leq \ sum _ {i = 1} ^ {n} \ | e_ {i} \ | \ cdot | x_ {i} | \ leq {\ sqrt {\ sum _ {i = 1} ^ {n} \ | e_ {i} \ | ^ {2}}} \ cdot {\ sqrt {\ sum _ {i = 1} ^ {n} | x_ {i} | ^ {2}}} = \ beta \ cdot \ | \ mathbf {x} \ | _ {2}}$${\ displaystyle \ beta: = {\ sqrt {\ sum _ {i = 1} ^ {n} \ | e_ {i} \ | ^ {2}}}}$
• Agora temos que encontrar um , para todos . Suponha que não existe tal . Então existe para todo a , tal isso . Defina uma segunda sequência por . Esta sequência é limitada porque . Então, por causa do teorema de Bolzano-Weierstrass , existe uma subsequência convergente com limite R ⁿ . Agora mostramos isso , mas , o que é uma contradição. É , porque e , então . Isso implica , então . Por outro lado , porque . Isso nunca pode ser verdade, então a suposição era falsa e existe tal . ${\ displaystyle \ alpha> 0}$${\ displaystyle \ alpha \ cdot \ | \ mathbf {x} \ | _ {2} \ leq \ | \ mathbf {x} \ |}$${\ displaystyle {\ textbf {x}} \ in \ mathbb {R} ^ {n}}$${\ displaystyle \ alpha}$${\ displaystyle k \ in \ mathbb {N}}$${\ displaystyle \ mathbf {x} _ {k} \ in \ mathbb {R} ^ {n}}$${\ displaystyle \ | \ mathbf {x} _ {k} \ | _ {2}> k \ cdot \ | \ mathbf {x} _ {k} \ |}$${\ displaystyle ({\ tilde {\ textbf {x}}} _ {k}) _ {k \ in \ mathbb {N}}}$${\ textstyle {\ tilde {\ mathbf {x}}} _ {k}: = {\ frac {\ mathbf {x} _ {k}} {\ | \ mathbf {x} _ {k} \ | _ { 2}}}}$${\ displaystyle \ | {\ tilde {\ mathbf {x}}} _ {k} \ | _ {2} = 1}$${\ displaystyle ({\ tilde {\ textbf {x}}} _ {k_ {j}}) _ {j \ in \ mathbb {N}}}$${\ displaystyle {\ textbf {a}} \ in}$ ${\ displaystyle \ | \ mathbf {a} \ | _ {2} = 1}$${\ displaystyle {\ textbf {a}} = {\ textbf {0}}}$${\ displaystyle \ | \ mathbf {a} \ | \ leq \ left \ | \ mathbf {a} - {\ tilde {\ mathbf {x}}} _ {k_ {j}} \ right \ | + \ left \ | {\ tilde {\ mathbf {x}}} _ {k_ {j}} \ direita \ | \ leq \ beta \ cdot \ left \ | \ mathbf {a} - {\ tilde {\ mathbf {x}}} _ {k_ {j}} \ right \ | _ {2} + {\ frac {\ | \ mathbf {x} _ {k_ {j}} \ |} {\ | \ mathbf {x} _ {k_ {j }} \ | _ {2}}} \ {\ overset {j \ to \ infty} {\ to}} \ 0}$${\ displaystyle \ | \ mathbf {a} - {\ tilde {\ mathbf {x}}} _ {k_ {j}} \ | \ to 0}$${\ displaystyle 0 \ leq {\ frac {\ | \ mathbf {x} _ {k_ {j}} \ |} {\ | \ mathbf {x} _ {k_ {j}} \ | _ {2}}} <{\ frac {1} {k_ {j}}}}$${\ displaystyle {\ frac {\ | {\ textbf {x}} _ {k_ {j}} \ |} {\ | \ mathbf {x} _ {k_ {j}} \ | _ {2}}} \ para 0}$${\ displaystyle \ | \ mathbf {a} \ | = 0}$${\ displaystyle {\ textbf {a}} = {\ textbf {0}}}$${\ displaystyle \ | \ mathbf {a} \ | _ {2} = 1}$${\ displaystyle \ | \ mathbf {a} \ | _ {2} = \ left \ | \ lim _ {j \ to \ infty} {\ tilde {\ textbf {x}}} _ {k_ {j}} \ direita \ | _ {2} = \ lim _ {j \ to \ infty} \ left \ | {\ tilde {\ textbf {x}}} _ {k_ {j}} \ right \ | _ {2} = 1 }$${\ displaystyle \ alpha> 0}$

Veja também

• Objeto exponencial , para explicação teórica da notação sobrescrita
• Espaço projetivo real

Notas de rodapé

Referências

• Kelley, John L. (1975). Topologia geral . Springer-Verlag. ISBN   0-387-90125-6 .
• Munkres, James (1999). Topologia . Prentice-Hall. ISBN   0-13-181629-2 .