Bivector - Bivector

Em matemática , um bivetor ou 2-vetor é uma quantidade na álgebra exterior ou álgebra geométrica que estende a ideia de escalares e vetores . Se um escalar é considerado uma quantidade de grau zero e um vetor é uma quantidade de grau um, então um bivetor pode ser considerado como tendo grau dois. Os bivetores têm aplicações em muitas áreas da matemática e da física. Eles estão relacionados a números complexos em duas dimensões e a pseudovetores e quatérnios em três dimensões. Eles podem ser usados ​​para gerar rotações em qualquer número de dimensões e são uma ferramenta útil para classificar essas rotações. Eles também são usados ​​na física , ligando uma série de quantidades não relacionadas de outra forma.

Bivectors são gerados pelo produto exterior em vectores: dado dois vectores de um e b , o produto exterior um ∧ b é um bivector, como é a soma de quaisquer bivectors. Nem todos os bivetores podem ser gerados como um único produto externo. Mais precisamente, um bivetor que pode ser expresso como um produto externo é chamado de simples ; em até três dimensões, todos os bivetores são simples, mas em dimensões superiores não é o caso. O produto exterior de dois vetores é alternado , então b ∧ a é a negação do bivetor a ∧ b , produzindo a orientação oposta, e a ∧ a é o bivetor zero.

Geometricamente, um bivetor simples pode ser interpretado como um segmento plano orientado , da mesma forma que os vetores podem ser considerados como segmentos de linha direcionados . O bivector um ∧ b tem uma magnitude igual à área do paralelogramo com arestas um e b , tem a atitude do plano gerado por um e b , e tem orientação sendo o sentido da rotação que alinham uma com b .

Em termos leigos, qualquer superfície é o mesmo bivetor, se tiver a mesma área, a mesma orientação e for paralela ao mesmo plano (ver figura).

História

O bivetor foi definido pela primeira vez em 1844 pelo matemático alemão Hermann Grassmann na álgebra exterior como resultado do produto exterior de dois vetores. Apenas no ano anterior, na Irlanda, William Rowan Hamilton havia descoberto quatérnios . Não foi até o matemático inglês William Kingdon Clifford em 1888 adicionar o produto geométrico à álgebra de Grassmann, incorporando as idéias de Hamilton e Grassmann, e fundar a álgebra de Clifford , que o bivetor como é conhecido hoje foi totalmente compreendido.

Por volta dessa época, Josiah Willard Gibbs e Oliver Heaviside desenvolveram o cálculo vetorial , que incluía produto vetorial e produtos escalares separados derivados da multiplicação do quatérnio. O sucesso do cálculo vetorial e do livro Vector Analysis, de Gibbs e Wilson , teve o efeito de que os insights de Hamilton e Clifford foram esquecidos por um longo tempo, uma vez que grande parte da matemática e da física do século 20 foi formulada em termos vetoriais. Gibbs usou vetores para preencher o papel de bivetores em três dimensões e usou "bivetores" para descrever uma quantidade não relacionada, um uso que às vezes foi copiado. Hoje, o bivetor é amplamente estudado como um tópico em álgebra geométrica , uma álgebra de Clifford sobre espaços vetoriais reais ou complexos com uma forma quadrática . Seu ressurgimento foi liderado por David Hestenes que, junto com outros, aplicou a álgebra geométrica a uma gama de novas aplicações na física .

Derivação

Para este artigo, o bivetor será considerado apenas em álgebras geométricas reais. Na prática, isso não é uma grande restrição, pois todos os aplicativos úteis são extraídos dessas álgebras. Além disso, a menos que indicado de outra forma, todos os exemplos têm uma métrica euclidiana e, portanto, uma forma quadrática definida positiva .

Álgebra geométrica e o produto geométrico

O bivetor surge da definição do produto geométrico sobre um espaço vetorial. Para vectores de um , b e c , o produto geométrico em vectores é definida como se segue:

Associatividade

${\ displaystyle (\ mathbf {ab}) \ mathbf {c} = \ mathbf {a} (\ mathbf {bc})}$

Distributividade esquerda e direita

${\ displaystyle {\ begin {alinhados} \ mathbf {a} (\ mathbf {b} + \ mathbf {c}) & = \ mathbf {ab} + \ mathbf {ac} \\ (\ mathbf {b} + \ mathbf {c}) \ mathbf {a} & = \ mathbf {ba} + \ mathbf {ca} \ end {alinhado}}}$

Contração

${\ displaystyle {\ mathbf {a}} ^ {2} = Q (\ mathbf {a}) = \ epsilon _ {\ mathbf {a}} {\ left | \ mathbf {a} \ right |} ^ {2 }}$

Onde Q é a forma quadrática, | a | é a magnitude de um e ε _um é a assinatura métrica . Para um espaço com métrica euclidiana ϵ _a é 1, então pode ser omitido, e a condição de contração torna-se:

${\ displaystyle {\ mathbf {a}} ^ {2} = {\ left | \ mathbf {a} \ right |} ^ {2}}$

O produto interior

Da associatividade, a ( ab ) = a ² b , a escalar vezes b . Quando b não é paralelo e, portanto, não é um múltiplo escalar de a , ab não pode ser um escalar. Mas

${\ displaystyle {\ frac {1} {2}} (\ mathbf {ab} + \ mathbf {ba}) = {\ frac {1} {2}} \ left ((\ mathbf {a} + \ mathbf { b}) ^ {2} - \ mathbf {a} ^ {2} - \ mathbf {b} ^ {2} \ right)}$

é uma soma de escalares e, portanto, um escalar. A partir da lei dos cossenos no triângulo formado pelos vetores seu valor é | a | | b | cos  θ , onde θ é o ângulo entre os vetores. É, portanto, idêntico ao produto interior entre dois vetores, e é escrito da mesma maneira,

${\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} = {\ frac {1} {2}} (\ mathbf {ab} + \ mathbf {ba}).}$

É simétrico, escalar valorizado, e pode ser usado para determinar o ângulo entre dois vectores: em particular, se um e b são ortogonais o produto é zero.

O produto exterior

Assim como o produto interno pode ser formulado como a parte simétrica do produto geométrico de outra quantidade, o produto externo (às vezes conhecido como produto "em cunha" ou "progressivo") pode ser formulado como sua parte anti-simétrica :

${\ displaystyle \ mathbf {a} \ wedge \ mathbf {b} = {\ frac {1} {2}} (\ mathbf {ab} - \ mathbf {ba})}$

É anti-simétrico em a e b

${\ displaystyle \ mathbf {b} \ wedge \ mathbf {a} = {\ frac {1} {2}} (\ mathbf {ba} - \ mathbf {ab}) = - {\ frac {1} {2} } (\ mathbf {ab} - \ mathbf {ba}) = - \ mathbf {a} \ wedge \ mathbf {b}}$

e por adição:

${\ displaystyle \ mathbf {a} \ cdot \ mathbf {b} + \ mathbf {a} \ wedge \ mathbf {b} = {\ frac {1} {2}} (\ mathbf {ab} + \ mathbf {ba }) + {\ frac {1} {2}} (\ mathbf {ab} - \ mathbf {ba}) = \ mathbf {ab}}$

Ou seja, o produto geométrico é a soma do produto interno simétrico e do produto externo anti-simétrico.

Para examinar a natureza de a ∧ b , considere a fórmula

${\ displaystyle (\ mathbf {a} \ cdot \ mathbf {b}) ^ {2} - (\ mathbf {a} \ wedge \ mathbf {b}) ^ {2} = \ mathbf {a} ^ {2} \ mathbf {b} ^ {2},}$

que usando a identidade trigonométrica pitagórica dá o valor de ( a ∧ b ) ²

${\ displaystyle (\ mathbf {a} \ wedge \ mathbf {b}) ^ {2} = (\ mathbf {a} \ cdot \ mathbf {b}) ^ {2} - \ mathbf {a} ^ {2} \ mathbf {b} ^ {2} = \ left | \ mathbf {a} \ right | ^ {2} \ left | \ mathbf {b} \ right | ^ {2} (\ cos ^ {2} \ theta - 1) = - \ left | \ mathbf {a} \ right | ^ {2} \ left | \ mathbf {b} \ right | ^ {2} \ sin ^ {2} \ theta}$

Com um quadrado negativo, ele não pode ser uma quantidade escalar ou vetorial, então é um novo tipo de objeto, um bivetor . Tem magnitude | a | | b | | sin  θ | , onde θ é o ângulo entre os vetores e, portanto, é zero para vetores paralelos.

Para distingui-los de vetores, bivetores são escritos aqui com maiúsculas em negrito, por exemplo:

${\ displaystyle \ mathbf {A} = \ mathbf {a} \ wedge \ mathbf {b} = - \ mathbf {b} \ wedge \ mathbf {a} \,}$

embora outras convenções sejam usadas, em particular porque vetores e bivetores são ambos elementos da álgebra geométrica.

Propriedades

O espaço ⋀ ² R ⁿ

A álgebra gerada pelo produto geométrico é a álgebra geométrica sobre o espaço vetorial. Para um espaço vetorial euclidiano escreve-se ou Cl _n ( R ), onde n é a dimensão do espaço vetorial R ⁿ . Cl _n ( R ) é um espaço vetorial e uma álgebra, gerado por todos os produtos entre vetores em R ⁿ , portanto, contém todos os vetores e bivetores. Mais precisamente como um espaço vetorial, ele contém os vetores e bivetores como subespaços lineares , embora não subálgebras (uma vez que o produto geométrico de dois vetores geralmente não é outro vetor). O espaço de todos os bivetores é escrito ⋀ ² R ⁿ . ${\ displaystyle {\ mathcal {G}} _ {n}}$

A subálgebra uniforme

A subálgebra gerada pelos bivetores é a subálgebra par da álgebra geométrica, escrita Cl⁺
_n( R ). Esta álgebra resulta da consideração de todos os produtos de escalares e bivetores gerados pelo produto geométrico. Tem dimensão 2 ^{n −1} , e contém ⋀ ² R ⁿ como um subespaço linear com dimensão 1/2n ( n - 1) (um número triangular ). Em duas e três dimensões, a subálgebra par contém apenas escalares e bivetores, e cada um é de particular interesse. Em duas dimensões do mesmo subálgebra é isomorfo com os números complexos , C , enquanto em três é isomorfa a quatérnions , H . Mais geralmente, a subálgebra uniforme pode ser usada para gerar rotações em qualquer dimensão e pode ser gerada por bivetores na álgebra.

Magnitude

Como observado na seção anterior a magnitude de um bivector simples, que é aquele que é o produto exterior de dois vetores a e b , é | a | | b | sen θ , onde θ é o ângulo entre os vetores. Está escrito | B |, onde B é o bivetor.

Para bivetores gerais, a magnitude pode ser calculada tomando a norma do bivetor considerado como um vetor no espaço ⋀ ² R ⁿ . Se a magnitude é zero, então todos os componentes do bivetor são zero, e o bivetor é o bivetor zero que, como elemento da álgebra geométrica, é igual ao zero escalar.

Unidade de bivetores

Um bivetor unitário é aquele com magnitude unitária. Ele pode ser derivado de qualquer bivetor diferente de zero, dividindo o bivetor por sua magnitude, ou seja

${\ displaystyle {\ frac {\ mathbf {B}} {\ left | \ mathbf {B} \ right |}}.}$

De particular interesse são os bivetores unitários formados a partir dos produtos da base padrão . Se e _i e e _j são vetores de base distintos, então o produto e _i ∧ e _j é um bivetor. Como os vetores são ortogonais, isso é apenas e _i e _j , escrito e _ij , com magnitude unitária, pois os vetores são vetores unitários . O conjunto de todos esses bivetores forma uma base para ⋀ ² R ⁿ . Por exemplo, em quatro dimensões a base para ⋀ ² R ⁴ é ( e ₁ e ₂ , e ₁ e ₃ , e ₁ e ₄ , e ₂ e ₃ , e ₂ e ₄ , e ₃ e ₄ ) ou ( e ₁₂ , e ₁₃ , e ₁₄ , e ₂₃ , e ₂₄ , e ₃₄ ).

Bivetores simples

O produto externo de dois vetores é um bivetor, mas nem todos os bivetores são produtos externos de dois vetores. Por exemplo, em quatro dimensões, o bivetor

${\ displaystyle \ mathbf {B} = \ mathbf {e} _ {1} \ wedge \ mathbf {e} _ {2} + \ mathbf {e} _ {3} \ wedge \ mathbf {e} _ {4} = \ mathbf {e} _ {1} \ mathbf {e} _ {2} + \ mathbf {e} _ {3} \ mathbf {e} _ {4} = \ mathbf {e} _ {12} + \ mathbf {e} _ {34}}$

não pode ser escrito como o produto exterior de dois vetores. Um bivetor que pode ser escrito como o produto exterior de dois vetores é simples. Em duas e três dimensões, todos os bivetores são simples, mas não em quatro ou mais dimensões; em quatro dimensões, cada bivetor é a soma de no máximo dois produtos externos. Um bivetor tem um quadrado real se e somente se for simples, e apenas bivetores simples podem ser representados geometricamente por uma área plana orientada.

Produto de dois bivetores

O produto geométrico de dois bivetores, A e B , é

${\ displaystyle \ mathbf {A} \ mathbf {B} = \ mathbf {A} \ cdot \ mathbf {B} + \ mathbf {A} \ times \ mathbf {B} + \ mathbf {A} \ wedge \ mathbf { B}.}$

A quantidade A ⋅ B é o produto interno com valor escalar, enquanto A ∧ B é o produto externo de grau 4 que surge em quatro ou mais dimensões. A quantidade A × B é o produto do comutador com valor bivetor , dado por

${\ displaystyle \ mathbf {A} \ times \ mathbf {B} = {\ frac {1} {2}} (\ mathbf {AB} - \ mathbf {BA}),}$

O espaço dos bivetores ⋀ ² R ⁿ são uma álgebra de Lie sobre R , com o produto do comutador como o suporte de Lie. O produto geométrico completo dos bivetores gera a subálgebra uniforme.

De particular interesse é o produto de um bivetor consigo mesmo. Como o produto do comutador é anti-simétrico, o produto simplifica para

${\ displaystyle \ mathbf {A} \ mathbf {A} = \ mathbf {A} \ cdot \ mathbf {A} + \ mathbf {A} \ wedge \ mathbf {A}.}$

Se o bivetor for simples, o último termo é zero e o produto é o valor escalar A ⋅ A , que pode ser usado como uma verificação da simplicidade. Em particular, o produto exterior dos bivetores só existe em quatro ou mais dimensões, então todos os bivetores em duas e três dimensões são simples.

Duas dimensões

Ao trabalhar com coordenadas em álgebra geométrica, é comum escrever os vetores de base como ( e ₁ , e ₂ , ...), uma convenção que será usada aqui.

Um vetor no espaço bidimensional real R ² pode ser escrito a = a ₁ e ₁ + a ₂ e ₂ , onde a ₁ e a ₂ são números reais, e ₁ e e ₂ são vetores de base ortonormal . O produto geométrico de dois desses vetores é

${\ displaystyle {\ begin {alinhado} \ mathbf {a} \ mathbf {b} & = (a_ {1} \ mathbf {e} _ {1} + a_ {2} \ mathbf {e} _ {2}) (b_ {1} \ mathbf {e} _ {1} + b_ {2} \ mathbf {e} _ {2}) \\ & = a_ {1} b_ {1} \ mathbf {e} _ {1} \ mathbf {e} _ {1} + a_ {1} b_ {2} \ mathbf {e} _ {1} \ mathbf {e} _ {2} + a_ {2} b_ {1} \ mathbf {e} _ {2} \ mathbf {e} _ {1} + a_ {2} b_ {2} \ mathbf {e} _ {2} \ mathbf {e} _ {2} \\ & = a_ {1} b_ { 1} + a_ {2} b_ {2} + (a_ {1} b_ {2} -a_ {2} b_ {1}) \ mathbf {e} _ {1} \ mathbf {e} _ {2}. \ end {alinhado}}}$

Isso pode ser dividido em um produto interno simétrico, com valor escalar e um produto externo antissimétrico com valor bivetor:

${\ displaystyle {\ begin {alinhados} \ mathbf {a} \ cdot \ mathbf {b} & = a_ {1} b_ {1} + a_ {2} b_ {2}, \\\ mathbf {a} \ wedge \ mathbf {b} & = (a_ {1} b_ {2} -a_ {2} b_ {1}) \ mathbf {e} _ {1} \ mathbf {e} _ {2} = (a_ {1} b_ {2} -a_ {2} b_ {1}) \ mathbf {e} _ {12}. \ end {alinhado}}}$

Todos os bivetores em duas dimensões são desta forma, isto é, múltiplos do bivetor e ₁ e ₂ , escrito e ₁₂ para enfatizar que é um bivetor ao invés de um vetor. A magnitude de e ₁₂ é 1, com

${\ displaystyle \ mathbf {e} _ {12} ^ {2} = - 1,}$

por isso é chamado de bivetor de unidade . O termo bivetor de unidade pode ser usado em outras dimensões, mas é definido exclusivamente (até um sinal) em duas dimensões e todos os bivetores são múltiplos de e ₁₂ . Como o elemento de maior nota da álgebra, e ₁₂ é também o pseudoescalar que recebe o símbolo i .

Números complexos

Com as propriedades de quadrado negativo e magnitude unitária, o bivetor de unidade pode ser identificado com a unidade imaginária de números complexos . Os bivectors e escalares em conjunto formam o mesmo subálgebra da álgebra geométrica, que é isomorfa a números complexo C . A subálgebra par tem base (1, e ₁₂ ), toda a álgebra tem base (1, e ₁ , e ₂ , e ₁₂ ).

Os números complexos são geralmente identificados com os eixos de coordenadas e vetores bidimensionais, o que significaria associá-los aos elementos vetoriais da álgebra geométrica. Não há contradição nisso, pois para passar de um vetor geral a um número complexo, um eixo precisa ser identificado como o eixo real, e ₁ digamos. Isso se multiplica por todos os vetores para gerar os elementos de até mesmo subálgebra.

Todas as propriedades dos números complexos podem ser derivadas de bivetores, mas duas são de particular interesse. Primeiro, como acontece com os produtos de números complexos de bivetores, as subálgebra pares são comutativas . Isso só é verdade em duas dimensões, portanto, as propriedades do bivetor em duas dimensões que dependem da comutatividade geralmente não se generalizam para dimensões superiores.

Em segundo lugar, um bivetor geral pode ser escrito

${\ displaystyle \ theta \ mathbf {e} _ {12} = i \ theta,}$

onde θ é um número real. Colocando isso na série de Taylor para o mapa exponencial e usando a propriedade e ₁₂ ² = −1 resulta em uma versão bivetora da fórmula de Euler ,

${\ displaystyle e ^ {\ theta \ mathbf {e} _ {12}} = e ^ {i \ theta} = \ cos {\ theta} + i \ sin {\ theta},}$

que, quando multiplicado por qualquer vetor, o gira através de um ângulo θ sobre a origem:

${\ displaystyle (x '\ mathbf {e} _ {1} + y' \ mathbf {e} _ {2}) = (x \ mathbf {e} _ {1} + y \ mathbf {e} _ {2 }) e ^ {i \ theta}.}$

O produto de um vetor com um bivetor em duas dimensões é anticommutativo , portanto, todos os produtos a seguir geram a mesma rotação

${\ displaystyle \ mathbf {v} '= \ mathbf {v} e ^ {i \ theta} = e ^ {- i \ theta} \ mathbf {v} = e ^ {\ frac {-i \ theta} {2 }} \ mathbf {v} e ^ {\ frac {i \ theta} {2}}.}$

Destes, o último produto é aquele que generaliza em dimensões superiores. A quantidade necessária é chamada de rotor e recebe o símbolo R , então, em duas dimensões, um rotor que gira através do ângulo θ pode ser escrito

${\ displaystyle R = e ^ {\ frac {-i \ theta} {2}} = e ^ {\ frac {- \ theta \ mathbf {e} _ {12}} {2}},}$

e a rotação que ele gera é

${\ displaystyle \ mathbf {v} '= R \ mathbf {v} R ^ {- 1}. \,}$

Três dimensões

Em três dimensões, o produto geométrico de dois vetores é

${\ displaystyle {\ begin {align} \ mathbf {ab} & = (a_ {1} \ mathbf {e} _ {1} + a_ {2} \ mathbf {e} _ {2} + a_ {3} \ mathbf {e} _ {3}) (b_ {1} \ mathbf {e} _ {1} + b_ {2} \ mathbf {e} _ {2} + b_ {3} \ mathbf {e} _ {3 }) \\ & = a_ {1} b_ {1} {\ mathbf {e} _ {1}} ^ {2} + a_ {2} b_ {2} {\ mathbf {e} _ {2}} ^ {2} + a_ {3} b_ {3} {\ mathbf {e} _ {3}} ^ {2} + (a_ {2} b_ {3} -a_ {3} b_ {2}) \ mathbf { e} _ {2} \ mathbf {e} _ {3} + (a_ {3} b_ {1} -a_ {1} b_ {3}) \ mathbf {e} _ {3} \ mathbf {e} _ {1} + (a_ {1} b_ {2} -a_ {2} b_ {1}) \ mathbf {e} _ {1} \ mathbf {e} _ {2}. \ End {alinhado}}}$

Isso pode ser dividido em produto interno simétrico, com valor escalar e produto externo, com valor bivetor, antissimétrico:

${\ displaystyle {\ begin {align} \ mathbf {a} \ cdot \ mathbf {b} & = a_ {1} b_ {1} + a_ {2} b_ {2} + a_ {3} b_ {3} \ \\ mathbf {a} \ wedge \ mathbf {b} & = (a_ {2} b_ {3} -a_ {3} b_ {2}) \ mathbf {e} _ {23} + (a_ {3} b_ {1} -a_ {1} b_ {3}) \ mathbf {e} _ {31} + (a_ {1} b_ {2} -a_ {2} b_ {1}) \ mathbf {e} _ {12 }. \ end {alinhado}}}$

Em três dimensões, todos os bivetores são simples e, portanto, o resultado de um produto exterior. As unidades bivetoras e ₂₃ , e ₃₁ e e ₁₂ formam uma base para o espaço dos bivetores ⋀ ² R ³ , que é, por sua vez, um espaço linear tridimensional. Portanto, se um bivetor geral é:

${\ displaystyle \ mathbf {A} = A_ {23} \ mathbf {e} _ {23} + A_ {31} \ mathbf {e} _ {31} + A_ {12} \ mathbf {e} _ {12} ,}$

eles podem ser adicionados como vetores

${\ displaystyle \ mathbf {A} + \ mathbf {B} = (A_ {23} + B_ {23}) \ mathbf {e} _ {23} + (A_ {31} + B_ {31}) \ mathbf { e} _ {31} + (A_ {12} + B_ {12}) \ mathbf {e} _ {12}.}$

enquanto, quando multiplicados, eles produzem o seguinte

${\ displaystyle \ mathbf {A} \ mathbf {B} = -A_ {23} B_ {23} -A_ {31} B_ {31} -A_ {12} B_ {12} + (A_ {12} B_ {31 } -A_ {31} B_ {12}) \ mathbf {e} _ {23} + (A_ {23} B_ {12} -A_ {12} B_ {23}) \ mathbf {e} _ {31} + (A_ {31} B_ {23} -A_ {23} B_ {31}) \ mathbf {e} _ {12}}$

que pode ser dividido em partes escalares simétricas e bivetoras antissimétricas da seguinte forma

${\ displaystyle {\ begin {align} \ mathbf {A} \ cdot \ mathbf {B} & = - A_ {12} B_ {12} -A_ {31} B_ {31} -A_ {23} B_ {23} \\\ mathbf {A} \ times \ mathbf {B} & = (A_ {23} B_ {31} -A_ {31} B_ {23}) \ mathbf {e} _ {12} + (A_ {12} B_ {23} -A_ {23} B_ {12}) \ mathbf {e} _ {13} + (A_ {31} B_ {12} -A_ {12} B_ {31}) \ mathbf {e} _ { 23}. \ End {alinhado}}}$

O produto externo de dois bivetores em três dimensões é zero.

Um bivetor B pode ser escrito como o produto de sua magnitude e um bivetor unitário, então escrevendo β para | B | e usando a série de Taylor para o mapa exponencial, pode-se mostrar que

${\ displaystyle e ^ {\ mathbf {B}} = e ^ {\ beta {\ frac {\ mathbf {B}} {\ beta}}} = \ cos {\ beta} + {\ frac {\ mathbf {B }} {\ beta}} \ sin {\ beta}.}$

Esta é outra versão da fórmula de Euler, mas com um bivetor geral em três dimensões. Ao contrário de duas dimensões, os bivetores não são comutativos, de modo que as propriedades que dependem da comutatividade não se aplicam a três dimensões. Por exemplo, em geral e ^{A + B} ≠ e ^A e ^B em três (ou mais) dimensões.

A álgebra geométrica completa em três dimensões, Cl ₃ ( R ), tem base (1, e ₁ , e ₂ , e ₃ , e ₂₃ , e ₃₁ , e ₁₂ , e ₁₂₃ ). O elemento e ₁₂₃ é um trivector e o pseudoescalar da geometria. Bivetores em três dimensões às vezes são identificados com pseudovetores aos quais estão relacionados, como discutido abaixo .

Quatérnions

Os bivetores não se fecham sob o produto geométrico, mas a subálgebra uniforme sim. Em três dimensões, consiste em todos os elementos escalares e bivetores da álgebra geométrica, então um elemento geral pode ser escrito, por exemplo a + A , onde a é a parte escalar e A é a parte bivetora. Está escrito em Cl⁺
₃e tem base (1, e ₂₃ , e ₃₁ , e ₁₂ ). O produto de dois elementos gerais da subálgebra uniforme é

${\ displaystyle (a + \ mathbf {A}) (b + \ mathbf {B}) = ab + a \ mathbf {B} + b \ mathbf {A} + \ mathbf {A} \ cdot \ mathbf {B} + \ mathbf {A} \ times \ mathbf {B}.}$

O subálgebra mesmo, que é o que consiste em álgebra escalares e bivectors, é isomorfa a quatérnions , H . Isto pode ser visto comparando a base para a base Quatérnion, ou a partir do produto acima do qual é idêntico ao produto Quatérnion, excepto por uma alteração de sinal que se refere aos produtos negativas no produto interior bivector Um ⋅ B . Outras propriedades do quatérnio podem ser relacionadas ou derivadas da álgebra geométrica.

Isso sugere que a divisão usual de um quaternion em partes escalares e vetoriais seria melhor representada como uma divisão em partes escalares e bivetoras; se isso for feito, o produto do quaternion é meramente o produto geométrico. Também relaciona quatérnios em três dimensões a números complexos em duas, pois cada um é isomórfico à subálgebra par da dimensão, uma relação que se generaliza para dimensões superiores.

Vetor de rotação

O vetor de rotação, a partir da representação do ângulo do eixo das rotações, é uma forma compacta de representar as rotações em três dimensões. Em sua forma mais compacta, consiste em um vetor, o produto de um vetor unitário ω que é o eixo de rotação com o ângulo de rotação (com sinal) θ , de modo que a magnitude do vetor de rotação geral θω é igual a (sem sinal) ângulo de rotação.

O quaternion associado à rotação é

${\ displaystyle q = \ left (\ cos \ left ({\ frac {\ theta} {2}} \ right), \ omega \ sin \ left ({\ frac {\ theta} {2}} \ right) \ direito)}$

Na álgebra geométrica, a rotação é representada por um bivetor. Isso pode ser visto em sua relação com os quatérnios. Seja Ω um bivetor unitário no plano de rotação e seja θ o ângulo de rotação . Então, o bivetor de rotação é Ω θ . O quaternion corresponde aproximadamente à exponencial da metade do bivetor Ω θ . Ou seja, os componentes do quatérnio correspondem às partes escalares e bivetoriais da seguinte expressão:

O exponencial pode ser definido em termos de sua série de potências e facilmente avaliado usando o fato de que Ω ao quadrado é −1.

Portanto, as rotações podem ser representadas por bivetores. Assim como os quatérnios são elementos da álgebra geométrica, eles estão relacionados pelo mapa exponencial dessa álgebra.

Rotores

O bivetor Ω θ gera uma rotação através do mapa exponencial. Os elementos pares gerados giram um vetor geral em três dimensões da mesma forma que os quatérnios:

Como em duas dimensões, a quantidade de e ^{- ohms q / 2} é chamado um rotor e escrita R . A quantidade e ^{Ω θ / 2} é então R ⁻¹ , e eles geram rotações como

Isso é idêntico a duas dimensões, exceto que aqui os rotores são objetos quadridimensionais isomórficos aos quatérnios. Isso pode ser generalizado para todas as dimensões, com rotores, elementos da subálgebra par com magnitude unitária, sendo gerados pelo mapa exponencial a partir de bivetores. Eles formam uma tampa dupla sobre o grupo de rotação, de modo que os rotores R e - R representam a mesma rotação.

Matrizes

Os bivetores são matrizes isomórficas a simétricas oblíquas ; o bivetor geral B ₂₃ e ₂₃ + B ₃₁ e ₃₁ + B ₁₂ e ₁₂ mapeia para a matriz

${\ displaystyle M_ {B} = {\ begin {pmatrix} 0 & B_ {12} & - B_ {31} \\ - B_ {12} & 0 & B_ {23} \\ B_ {31} & - B_ {23} & 0 \ end {pmatriz}}.}$

Isto multiplicado por vetores em ambos os lados dá o mesmo vetor que o produto de um vetor e bivetor menos o produto externo; um exemplo é o tensor de velocidade angular .

Matrizes simétricas enviesadas geram matrizes ortogonais com determinante 1 por meio do mapa exponencial. Em particular, o expoente de um bivetor associado a uma rotação é uma matriz de rotação , ou seja, a matriz de rotação M _R dada pela matriz simétrica inclinada acima é

${\ displaystyle M_ {R} = e ^ {M_ {B}}.}$

A rotação descrita por M _R é a mesma descrita pelo rotor R dado por

${\ displaystyle R = e ^ {\ frac {B} {2}},}$

e a matriz M _R também pode ser calculada diretamente do rotor R :

${\ displaystyle M_ {R} = {\ begin {pmatrix} (R \ mathbf {e} _ {1} R ^ {- 1}) \ cdot \ mathbf {e} _ {1} & (R \ mathbf {e } _ {2} R ^ {- 1}) \ cdot \ mathbf {e} _ {1} & (R \ mathbf {e} _ {3} R ^ {- 1}) \ cdot \ mathbf {e} _ {1} \\ (R \ mathbf {e} _ {1} R ^ {- 1}) \ cdot \ mathbf {e} _ {2} & (R \ mathbf {e} _ {2} R ^ {- 1}) \ cdot \ mathbf {e} _ {2} & (R \ mathbf {e} _ {3} R ^ {- 1}) \ cdot \ mathbf {e} _ {2} \\ (R \ mathbf {e} _ {1} R ^ {- 1}) \ cdot \ mathbf {e} _ {3} & (R \ mathbf {e} _ {2} R ^ {- 1}) \ cdot \ mathbf {e } _ {3} & (R \ mathbf {e} _ {3} R ^ {- 1}) \ cdot \ mathbf {e} _ {3} \ end {pmatrix}}.}$

Os bivetores estão relacionados aos autovalores de uma matriz de rotação. Dada uma matriz de rotação M, os valores próprios podem ser calculados resolvendo a equação característica para essa matriz 0 = det ( M - λ I ) . Pelo teorema fundamental da álgebra, isso tem três raízes (apenas uma das quais é real, pois há apenas um autovetor, ou seja, o eixo de rotação). As outras raízes devem ser um par conjugado complexo. Eles têm magnitude unitária logaritmos puramente imaginários, igual à magnitude do bivetor associado à rotação, que também é o ângulo de rotação. Os autovetores associados aos autovalores complexos estão no plano do bivetor, de modo que o produto externo de dois autovetores não paralelos resulta no bivetor (ou em um múltiplo dele).

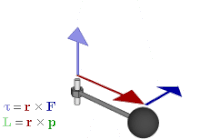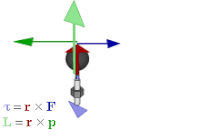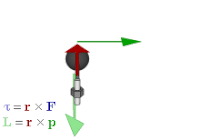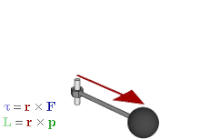
Vetores axiais

O vetor de rotação é um exemplo de vetor axial . Vetores axiais, ou pseudovetores, são vetores com a característica especial de suas coordenadas sofrerem uma mudança de sinal em relação aos vetores usuais (também chamados de "vetores polares") sob inversão através da origem, reflexão em um plano ou outra transformação linear de reversão de orientação . Os exemplos incluem quantidades como torque , momento angular e campos magnéticos vetoriais . Quantidades que usariam vetores axiais em álgebra vetorial são adequadamente representadas por bivetores em álgebra geométrica. Mais precisamente, se uma orientação subjacente for escolhida, os vetores axiais são naturalmente identificados com os vetores usuais; o dual de Hodge então fornece o isomorfismo entre vetores axiais e bivetores, de modo que cada vetor axial está associado a um bivetor e vice-versa; isso é

${\ displaystyle \ mathbf {A} = * \ mathbf {a} \ ,, \ quad \ mathbf {a} = * \ mathbf {A}}$

onde ∗ indica o Hodge dual. Observe que se a orientação subjacente for revertida por inversão através da origem, tanto a identificação dos vetores axiais com os vetores usuais quanto o sinal duplo de Hodge mudam, mas os bivetores não se movem. Alternativamente, usando a unidade pseudoescalar em Cl ₃ ( R ), i = e ₁ e ₂ e ₃ dá

${\ displaystyle \ mathbf {A} = \ mathbf {a} i \ ,, \ quad \ mathbf {a} = - \ mathbf {A} i.}$

É mais fácil de usar porque o produto é apenas o produto geométrico. Mas é anti-simétrico porque (como em duas dimensões) a unidade pseudoescalar i eleva ao quadrado a -1, então um negativo é necessário em um dos produtos.

Essa relação se estende a operações como o produto vetorial com valor vetorial e produto externo com valor bivetor, pois, quando escritos como determinantes , são calculados da mesma maneira:

${\ displaystyle \ mathbf {a} \ times \ mathbf {b} = {\ begin {vmatrix} \ mathbf {e} _ {1} & \ mathbf {e} _ {2} & \ mathbf {e} _ {3 } \\ a_ {1} & a_ {2} & a_ {3} \\ b_ {1} & b_ {2} & b_ {3} \ end {vmatrix}} \ ,, \ quad \ mathbf {a} \ wedge \ mathbf { b} = {\ begin {vmatrix} \ mathbf {e} _ {23} & \ mathbf {e} _ {31} & \ mathbf {e} _ {12} \\ a_ {1} & a_ {2} & a_ { 3} \\ b_ {1} & b_ {2} & b_ {3} \ end {vmatrix}} \,}$

então são relacionados pelo Hodge dual:

${\ displaystyle {* (\ mathbf {a} \ wedge \ mathbf {b})} = \ mathbf {a \ times b} \ ,, \ quad {* (\ mathbf {a \ times b})} = \ mathbf {a} \ wedge \ mathbf {b}.}$

Os bivetores têm uma série de vantagens sobre os vetores axiais. Eles desambiguem melhor os vetores axiais e polares, ou seja, as quantidades por eles representadas, de forma que fique mais claro quais operações são permitidas e quais são seus resultados. Por exemplo, o produto interno de um vetor polar e um vetor axial resultante do produto vetorial no produto triplo deve resultar em um pseudoescalar , um resultado que é mais óbvio se o cálculo for enquadrado como o produto externo de um vetor e bivetor. Eles generalizam para outras dimensões; em particular, os bivetores podem ser usados ​​para descrever quantidades como torque e momento angular em duas ou três dimensões. Além disso, eles se aproximam da intuição geométrica de várias maneiras, como visto na próxima seção.

Interpretação geométrica

Como sugere seu nome e o da álgebra, um dos atrativos dos bivetores é que possuem uma interpretação geométrica natural. Isso pode ser descrito em qualquer dimensão, mas é melhor feito em três, onde os paralelos podem ser desenhados com objetos mais familiares, antes de serem aplicados a dimensões superiores. Em duas dimensões, a interpretação geométrica é trivial, pois o espaço é bidimensional, portanto, tem apenas um plano, e todos os bivetores estão associados a ele, diferindo apenas por um fator de escala.

Todos os bivetores podem ser interpretados como planos ou, mais precisamente, como segmentos planos direcionados. Em três dimensões, existem três propriedades de um bivetor que podem ser interpretadas geometricamente:

• A disposição do plano no espaço, precisamente a atitude do plano (ou alternativamente a rotação , orientação geométrica ou gradiente do plano), está associada à proporção dos componentes bivetores. Em particular, os bivetores de três bases, e ₂₃ , e ₃₁ e e ₁₂ , ou múltiplos escalares deles, estão associados ao plano yz , plano zx e plano xy respectivamente.
• A magnitude do bivetor está associada à área do segmento do plano. A área não tem um formato específico, portanto, qualquer formato pode ser usado. Pode até ser representado de outras maneiras, como por uma medida angular. Mas se os vetores são interpretados como comprimentos, o bivetor é geralmente interpretado como uma área com as mesmas unidades, como segue.
• Como a direção de um vetor, um plano associado a um bivetor tem uma direção, uma circulação ou um sentido de rotação no plano, que assume dois valores vistos no sentido horário e anti-horário quando visto do ponto de vista que não está no plano. Isso está associado a uma mudança de sinal no bivetor, ou seja, se a direção for invertida, o bivetor será negado. Alternativamente, se dois bivetores têm a mesma atitude e magnitude, mas direções opostas, um é o negativo do outro.
• Se imaginado como um paralelogramo, com a origem dos vetores em 0, então a área com sinal é o determinante das coordenadas cartesianas dos vetores ( a _x b _y - b _x a _y ).

Em três dimensões, todos os bivetores podem ser gerados pelo produto exterior de dois vetores. Se o bivetor B = a ∧ b, então a magnitude de B é

${\ displaystyle \ left | \ mathbf {B} \ right | = \ left | \ mathbf {a} \ right | \ left | \ mathbf {b} \ right | \ sin {\ theta},}$

onde θ é o ângulo entre os vetores. Esta é a área do paralelogramo com arestas um e b , como mostrado no diagrama. Uma interpretação é que a área é varrida por b à medida que se move ao longo de a . O produto exterior é anti-simétrica, para que a inversão da ordem de um e b para fazer um movimento ao longo de b resulta em um bivector com a direcção oposta que é o negativo da primeira. O plano de bivector um ∧ b contém tanto um e b , de forma que estão tanto paralelo ao plano.

Bivetores e vetores axiais são relacionados por Hodge dual . Em um espaço vetorial real, o dual de Hodge relaciona um subespaço ao seu complemento ortogonal ; portanto, se um bivetor é representado por um plano, o vetor axial associado a ele é simplesmente a normal da superfície do plano . O plano tem duas normais, uma de cada lado, dando as duas orientações possíveis para o plano e bivetor.

Isto relaciona-se o produto passe para o produto exterior . Também pode ser usado para representar quantidades físicas, como torque e momento angular . Na álgebra vetorial, eles são geralmente representados por vetores, perpendiculares ao plano da força , momento linear ou deslocamento a partir dos quais são calculados. Mas se um bivetor for usado em vez disso, o plano é o plano do bivetor, então é uma maneira mais natural de representar as quantidades e a maneira como elas agem. Também ao contrário da representação vetorial se generaliza em outras dimensões.

O produto de dois bivetores tem uma interpretação geométrica. Para bivetores diferentes de zero A e B, o produto pode ser dividido em partes simétricas e antissimétricas da seguinte forma:

${\ displaystyle \ mathbf {AB} = \ mathbf {A} \ cdot \ mathbf {B} + \ mathbf {A} \ times \ mathbf {B}.}$

Assim como os vetores, eles têm magnitudes | A ⋅ B | = | A | | B | cos θ e | A × B | = | A | | B | sen θ , onde θ é o ângulo entre os planos. Em três dimensões, é o mesmo que o ângulo entre os vetores normais duais aos planos, e se generaliza até certo ponto em dimensões superiores.

Os bivetores podem ser adicionados juntos como áreas. Dadas duas diferentes de zero bivectors B e C em três dimensões, é sempre possível encontrar um vetor que está contido em ambos, uma palavra a dizer, por isso os bivectors pode ser escrita como produtos exteriores envolvendo um :

${\ displaystyle {\ begin {alinhados} \ mathbf {B} & = \ mathbf {a} \ wedge \ mathbf {b} \\\ mathbf {C} & = \ mathbf {a} \ wedge \ mathbf {c} \ fim {alinhado}}}$

Isso pode ser interpretado geometricamente como visto no diagrama: as duas áreas somam para dar uma terceira, com as três áreas formando faces de um prisma com a , b , c e b + c como arestas. Isso corresponde às duas formas de cálculo da área usando a distributividade do produto externo:

${\ displaystyle {\ begin {alinhados} \ mathbf {B} + \ mathbf {C} & = \ mathbf {a} \ wedge \ mathbf {b} + \ mathbf {a} \ wedge \ mathbf {c} \\ & = \ mathbf {a} \ wedge (\ mathbf {b} + \ mathbf {c}). \ end {alinhado}}}$

Isso só funciona em três dimensões, pois é a única dimensão onde um vetor paralelo a ambos os bivetores deve existir. Em dimensões superiores, os bivetores geralmente não estão associados a um único plano, ou se forem (bivetores simples), dois bivetores podem não ter nenhum vetor em comum e, portanto, somam um bivetor não simples.

Quatro dimensões

Em quatro dimensões os elementos de base para o espaço ⋀ ² R ⁴ dos bivetores são ( e ₁₂ , e ₁₃ , e ₁₄ , e ₂₃ , e ₂₄ , e ₃₄ ), então um bivetor geral é da forma

${\ displaystyle \ mathbf {A} = a_ {12} \ mathbf {e} _ {12} + a_ {13} \ mathbf {e} _ {13} + a_ {14} \ mathbf {e} _ {14} + a_ {23} \ mathbf {e} _ {23} + a_ {24} \ mathbf {e} _ {24} + a_ {34} \ mathbf {e} _ {34}.}$

Ortogonalidade

Em quatro dimensões, o Hodge dual de um bivetor é um bivetor, e o espaço ⋀ ² R ⁴ é dual a si mesmo. Os vetores normais não são únicos, em vez disso, cada plano é ortogonal a todos os vetores em seu espaço dual de Hodge. Isso pode ser usado para dividir os bivetores em duas 'metades', da seguinte maneira. Temos três pares de bivetores ortogonais: ( e ₁₂ , e ₃₄ ), ( e ₁₃ , e ₂₄ ) e ( e ₁₄ , e ₂₃ ). Existem quatro maneiras distintas de escolher um bivetor de cada um dos dois primeiros pares, e uma vez que esses dois primeiros são escolhidos, sua soma resulta no terceiro bivetor do outro par. Por exemplo, ( e ₁₂ , e ₁₃ , e ₁₄ ) e ( e ₂₃ , e ₂₄ , e ₃₄ ).

Bivetores simples em 4D

Em quatro dimensões, os bivetores são gerados pelo produto exterior dos vetores em R ⁴ , mas com uma diferença importante de R ³ e R ² . Em quatro dimensões, nem todos os bivetores são simples. Existem bivetores como e ₁₂ + e ₃₄ que não podem ser gerados pelo produto exterior de dois vetores. Isso também significa que eles não têm um quadrado real, ou seja, escalar. Nesse caso

${\ displaystyle (\ mathbf {e} _ {12} + \ mathbf {e} _ {34}) ^ {2} = \ mathbf {e} _ {12} \ mathbf {e} _ {12} + \ mathbf {e} _ {12} \ mathbf {e} _ {34} + \ mathbf {e} _ {34} \ mathbf {e} _ {12} + \ mathbf {e} _ {34} \ mathbf {e} _ {34} = - 2 + 2 \ mathbf {e} _ {1234}.}$

O elemento e ₁₂₃₄ é o pseudoescalar em Cl ₄ , distinto do escalar, portanto o quadrado é não escalar.

Todos os bivetores em quatro dimensões podem ser gerados usando no máximo dois produtos externos e quatro vetores. O bivetor acima pode ser escrito como

${\ displaystyle \ mathbf {e} _ {12} + \ mathbf {e} _ {34} = \ mathbf {e} _ {1} \ wedge \ mathbf {e} _ {2} + \ mathbf {e} _ {3} \ wedge \ mathbf {e} _ {4}.}$

Da mesma forma, cada bivetor pode ser escrito como a soma de dois bivetores simples. É útil escolher dois bivetores ortogonais para isso, e isso sempre é possível fazer. Além disso, para um bivetor genérico, a escolha de bivetores simples é única, ou seja, há apenas uma maneira de decompor em bivetores ortogonais; a única exceção é quando os dois bivetores ortogonais têm magnitudes iguais (como no exemplo acima): neste caso, a decomposição não é única. A decomposição é sempre única no caso de bivetores simples, com a vantagem adicional de que uma das partes ortogonais é zero.

Rotações em R ⁴

Como em três dimensões, bivetores em quatro dimensões geram rotações através do mapa exponencial, e todas as rotações podem ser geradas desta forma. Como em três dimensões, se B é um bivetor, o rotor R é e ^{B / 2} e as rotações são geradas da mesma maneira:

${\ displaystyle v '= RvR ^ {- 1}. \,}$

As rotações geradas são mais complexas. Eles podem ser categorizados da seguinte forma:

rotações simples são aquelas que fixam um plano em 4D e giram por um ângulo "em torno" deste plano.

as rotações duplas têm apenas um ponto fixo, a origem, e giram em dois ângulos em torno de dois planos ortogonais. Em geral, os ângulos são diferentes e os planos são especificados exclusivamente

rotações isoclínicas são rotações duplas onde os ângulos de rotação são iguais. Nesse caso, os planos sobre os quais a rotação está ocorrendo não são únicos.

Eles são gerados por bivetores de forma direta. Rotações simples são geradas por bivetores simples, com o plano fixo sendo dual ou ortogonal ao plano do bivetor. Pode-se dizer que a rotação ocorre em torno desse plano, no plano do bivetor. Todos os outros bivetores geram rotações duplas, com os dois ângulos de rotação iguais às magnitudes dos dois bivetores simples dos quais o bivetor não simples é composto. As rotações isoclínicas surgem quando essas magnitudes são iguais, caso em que a decomposição em dois bivetores simples não é única.

Os bivetores em geral não comutam, mas uma exceção são os bivetores ortogonais e seus expoentes. Portanto, se o bivetor B = B ₁ + B ₂ , onde B ₁ e B ₂ são bivetores simples ortogonais, é usado para gerar uma rotação, ele se decompõe em duas rotações simples que comutam da seguinte maneira:

${\ displaystyle R = e ^ {\ frac {\ mathbf {B} _ {1} + \ mathbf {B} _ {2}} {2}} = e ^ {\ frac {\ mathbf {B} _ {1 }} {2}} e ^ {\ frac {\ mathbf {B} _ {2}} {2}} = e ^ {\ frac {\ mathbf {B} _ {2}} {2}} e ^ { \ frac {\ mathbf {B} _ {1}} {2}}}$

Sempre é possível fazer isso, pois todos os bivetores podem ser expressos como somas de bivetores ortogonais.

Rotações do espaço-tempo

O espaço-tempo é um modelo matemático para o nosso universo usado na relatividade especial. Consiste em três dimensões espaciais e uma dimensão de tempo combinadas em um único espaço quadridimensional. É descrito naturalmente usando álgebra geométrica e bivetores, com a métrica euclidiana substituída por uma métrica de Minkowski . Essa álgebra é idêntica à do espaço euclidiano, exceto que a assinatura é alterada, então

${\ displaystyle {\ mathbf {e} _ {i}} ^ {2} = {\ begin {cases} 1, & i = 1,2,3 \\ - 1, & i = 4 \ end {cases}}}$

(Observe que a ordem e os índices acima não são universais - aqui e ₄ é a dimensão temporal). A álgebra geométrica é Cl _3,1 ( R ), e o subespaço dos bivetores é ⋀ ² R ^3,1 .

Os bivetores simples são de dois tipos. Os bivetores simples e ₂₃ , e ₃₁ e e ₁₂ têm quadrados negativos e abrangem os bivetores do subespaço tridimensional correspondente ao espaço euclidiano, R ³ . Esses bivetores geram rotações normais em R ³ .

Os bivetores simples e ₁₄ , e ₂₄ e e ₃₄ têm quadrados positivos e, como planos, abrangem uma dimensão espacial e a dimensão temporal. Eles também geram rotações por meio do mapa exponencial, mas em vez de funções trigonométricas, funções hiperbólicas são necessárias, o que gera um rotor da seguinte maneira:

${\ displaystyle e ^ {\ frac {{\ boldsymbol {\ Omega}} \ theta} {2}} = \ cosh \ left ({\ frac {\ theta} {2}} \ right) + {\ boldsymbol {\ Omega}} \ sinh \ left ({\ frac {\ theta} {2}} \ right),}$

onde Ω é o bivetor ( e ₁₄ , etc.), identificado pela métrica com uma transformação linear antissimétrica de R ^3,1 . Esses são boosts de Lorentz , expressos de uma forma particularmente compacta, usando o mesmo tipo de álgebra que em R ³ e R ⁴ .

Em geral, todas as rotações do espaço-tempo são geradas a partir de bivetores por meio do mapa exponencial, ou seja, um rotor geral gerado pelo bivetor A tem a forma

${\ displaystyle R = e ^ {\ frac {\ mathbf {A}} {2}}.}$

O conjunto de todas as rotações no espaço-tempo forma o grupo de Lorentz , e a partir deles a maioria das consequências da relatividade especial pode ser deduzida. De forma mais geral, isso mostra como as transformações no espaço euclidiano e no espaço-tempo podem ser descritas usando o mesmo tipo de álgebra.

Equações de Maxwell

(Observação: nesta seção os três vetores tradicionais são indicados por linhas sobre os símbolos e o vetor espaço-tempo e os bivetores por símbolos em negrito, com os vetores J e A excepcionalmente em maiúsculas)

As equações de Maxwell são usadas na física para descrever a relação entre os campos elétricos e magnéticos . Normalmente dadas como quatro equações diferenciais, elas têm uma forma particularmente compacta quando os campos são expressos como um bivetor do espaço-tempo de ⋀ ² R ^3,1 . Se os campos elétricos e magnéticos em R ³ são E e B, então o bivetor eletromagnético é

${\ displaystyle \ mathbf {F} = {\ frac {1} {c}} {\ overline {E}} \ mathbf {e} _ {4} + {\ overline {B}} \ mathbf {e} _ { 123},}$

onde e ₄ é novamente o vetor base para a dimensão semelhante ao tempo ec é a velocidade da luz . O produto B e ₁₂₃ produz o bivetor que é Hodge dual a B em três dimensões, como discutido acima , enquanto E e ₄ como um produto de vetores ortogonais também tem valor bivetor. Como um todo, é o tensor eletromagnético expresso de forma mais compacta como um bivetor e é usado da seguinte maneira. Primeiro, ele está relacionado à corrente J de 4 , uma grandeza vetorial dada por

${\ displaystyle \ mathbf {J} = {\ overline {j}} + c \ rho \ mathbf {e} _ {4},}$

onde j é a densidade de corrente e ρ é a densidade de carga . Eles estão relacionados por um operador diferencial ∂, que é

${\ displaystyle \ partial = \ nabla - \ mathbf {e} _ {4} {\ frac {1} {c}} {\ frac {\ partial} {\ partial t}}.}$

O operador ∇ é um operador diferencial em álgebra geométrica, agindo sobre as dimensões do espaço e dada por ∇ M = ∇⋅ M + ∇∧ M . Quando aplicado aos vetores, ∇⋅ M é a divergência e ∇∧ M é o cacho, mas com um resultado bivetor em vez de vetor, que é dual em três dimensões em relação ao cacho. Para a quantidade geral M, eles atuam como operadores diferenciais de redução e elevação de nível. Em particular, se M é um escalar, então esse operador é apenas o gradiente e pode ser considerado um operador geométrico algébrico del .

Juntos, eles podem ser usados ​​para fornecer uma forma particularmente compacta para as equações de Maxwell com fontes:

${\ displaystyle \ partial \ mathbf {F} = \ mathbf {J}.}$

Essa equação, quando decomposta de acordo com a álgebra geométrica, usando produtos geométricos que têm efeitos de aumento e redução de grau, é equivalente às quatro equações de Maxwell. Também está relacionado ao quatro potencial eletromagnético , um vetor A dado por

${\ displaystyle \ mathbf {A} = {\ overline {A}} + {\ frac {1} {c}} V \ mathbf {e} _ {4},}$

onde A é o potencial magnético vetorial e V é o potencial elétrico. Está relacionado ao bivetor eletromagnético da seguinte forma

${\ displaystyle \ partial \ mathbf {A} = - \ mathbf {F},}$

usando o mesmo operador diferencial ∂.

Dimensões superiores

Como foi sugerido nas seções anteriores, grande parte da álgebra geométrica generaliza-se bem em dimensões superiores. A álgebra geométrica para o espaço real R ⁿ é Cl _n ( R ), e o subespaço dos bivetores é ⋀ ² R ⁿ .

O número de bivetores simples necessários para formar um bivetor geral aumenta com a dimensão, então para n ímpar é ( n - 1) / 2 , para n par é n / 2 . Portanto, para quatro e cinco dimensões, apenas dois bivetores simples são necessários, mas três são necessários para seis e sete dimensões. Por exemplo, em seis dimensões com base padrão ( e ₁ , e ₂ , e ₃ , e ₄ , e ₅ , e ₆ ) o bivetor

${\ displaystyle \ mathbf {e} _ {12} + \ mathbf {e} _ {34} + \ mathbf {e} _ {56}}$

é a soma de três bivetores simples, mas não menos. Como em quatro dimensões é sempre possível encontrar bivetores simples ortogonais para esta soma.

Rotações em dimensões superiores

Como em rotores de três e quatro dimensões são gerados pelo mapa exponencial, então

${\ displaystyle e ^ {\ frac {\ mathbf {B}} {2}}}$

é o rotor gerado por bivector B . Rotações simples, que ocorrem em um plano de rotação em torno de uma lâmina fixa de dimensão ( n - 2) são geradas por bivetores simples, enquanto outros bivetores geram rotações mais complexas que podem ser descritas em termos de bivetores simples que são a soma de, cada um relacionado a um plano de rotação. Todos os bivetores podem ser expressos como a soma de bivetores simples ortogonais e comutativos, de modo que as rotações sempre podem ser decompostas em um conjunto de rotações comutativas em torno dos planos associados a esses bivetores. O grupo de rotores em n dimensões é o grupo de spin , Spin ( n ).

Uma característica notável, relacionada ao número de bivetores simples e planos de rotação, é que em dimensões ímpares cada rotação tem um eixo fixo - é enganoso chamá-lo de eixo de rotação, pois em dimensões superiores as rotações ocorrem em vários planos ortogonais para isso. Isso está relacionado aos bivetores, já que bivetores em dimensões ímpares se decompõem no mesmo número de bivetores que a dimensão par abaixo, portanto, têm o mesmo número de planos, mas uma dimensão extra. Como cada plano gera rotações em duas dimensões em dimensões ímpares, deve haver uma dimensão, que é um eixo, que não está sendo girado.

Os bivetores também estão relacionados à matriz de rotação em n dimensões. Como em três dimensões, a equação característica da matriz pode ser resolvida para encontrar os autovalores . Em dimensões ímpares, ele tem uma raiz real, com o autovetor o eixo fixo e, em dimensões pares, não tem raízes reais, de modo que todas ou todas as raízes, exceto uma, são pares conjugados complexos. Cada par está associado a um componente simples do bivetor associado à rotação. Em particular, o log de cada par é ± a magnitude, enquanto os autovetores gerados a partir das raízes são paralelos e, portanto, podem ser usados ​​para gerar o bivetor. Em geral, os autovalores e bivetores são únicos, e o conjunto de autovalores fornece a decomposição completa em bivetores simples; se as raízes são repetidas, a decomposição do bivetor em bivetores simples não é única.

Geometria projetiva

A álgebra geométrica pode ser aplicada à geometria projetiva de maneira direta. A álgebra geométrica usada é Cl _n ( R ), n ≥ 3 , a álgebra do espaço vetorial real R ⁿ . É usado para descrever objetos no espaço projetivo real RP ^{n −1} . Os vetores diferentes de zero em Cl _n ( R ) ou R ⁿ estão associados a pontos no espaço projetivo, de modo que vetores que diferem apenas por um fator de escala, de modo que seu produto exterior é zero, mapeiam para o mesmo ponto. Os bivetores simples diferentes de zero em ⋀ ² R ⁿ representam as linhas em RP ^{n −1} , com os bivetores diferindo apenas por um fator de escala (positivo ou negativo) que representa a mesma linha.

Uma descrição da geometria projetiva pode ser construída na álgebra geométrica usando operações básicas. Por exemplo, dados dois pontos distintos em RP ^{n -1} representado por vectores de um e b a linha contendo os mesmos é dada por um ∧ b (ou b ∧ um ). Duas linhas se intersectam num ponto de se Um ∧ B = 0 para as suas bivectors A e B . Este ponto é dado pelo vetor

${\ displaystyle \ mathbf {p} = \ mathbf {A} \ lor \ mathbf {B} = (\ mathbf {A} \ times \ mathbf {B}) J ^ {- 1}.}$

A operação "∨" é o encontro, que pode ser definido como acima, em termos do juntar, J = Um ∧ B para diferente de zero Um ∧ B . Usando essas operações, a geometria projetiva pode ser formulada em termos de álgebra geométrica. Por exemplo, dado um terceiro bivetor C (diferente de zero), o ponto p encontra-se na linha dada por C se e somente se

${\ displaystyle \ mathbf {p} \ land \ mathbf {C} = 0.}$

Portanto, a condição para as linhas dadas por A , B e C serem colineares é

${\ displaystyle (\ mathbf {A} \ lor \ mathbf {B}) \ land \ mathbf {C} = 0,}$

que em Cl ₃ ( R ) e RP ² simplifica para

${\ displaystyle \ langle \ mathbf {ABC} \ rangle = 0,}$

onde os colchetes indicam a parte escalar do produto geométrico. Da mesma forma, todas as operações espaciais projetivas podem ser escritas em termos de álgebra geométrica, com bivetores representando linhas gerais no espaço projetivo, de modo que toda a geometria pode ser desenvolvida usando álgebra geométrica.

Tensores e matrizes

Conforme observado acima, um bivetor pode ser escrito como uma matriz simétrica inclinada, que por meio do mapa exponencial gera uma matriz de rotação que descreve a mesma rotação do rotor, também gerada pelo mapa exponencial, mas aplicada ao vetor. Mas também é usado com outros bivetores, como o tensor de velocidade angular e o tensor eletromagnético , respectivamente uma matriz ou tensor de simetria oblíqua 3 × 3 e 4 × 4.

Os bivetores reais em ⋀ ² R ⁿ são isomórficos a matrizes com simetria n × n ou, alternativamente, a tensores antisimétricos de grau 2 em R ⁿ . Embora os bivetores sejam isomórficos aos vetores (via dual) em três dimensões, eles podem ser representados por matrizes assimétricas em qualquer dimensão. Isso é útil para relacionar bivetores a problemas descritos por matrizes, de modo que eles possam ser reformulados em termos de bivetores, dada uma interpretação geométrica, então muitas vezes resolvidos mais facilmente ou relacionados geometricamente a outros problemas de bivetores.

Mais geralmente, toda álgebra geométrica real é isomórfica a uma álgebra matricial . Eles contêm bivetores como um subespaço, embora frequentemente de uma forma que não é especialmente útil. Essas matrizes são de interesse principalmente como uma forma de classificar álgebras de Clifford.

Veja também

• Multivetor
• Álgebra multilinear

Notas

Referências gerais

• Leo Dorst; Daniel Fontijne; Stephen Mann (2009). "§ 2.3.3 Visualizando bivetores" . Álgebra Geométrica para Ciência da Computação: Uma Abordagem Orientada a Objetos para Geometria (2ª ed.). Morgan Kaufmann. p. 31 ff . ISBN 978-0-12-374942-0.
• Whitney, Hassler (1957). Teoria da Integração Geométrica . Princeton: Princeton University Press . ISBN 978-0-486-44583-0.

• Lounesto, Pertti (2001). Álgebras e espinores de Clifford . Cambridge: Cambridge University Press . ISBN 978-0-521-00551-7.

• Chris Doran e Anthony Lasenby (2003). "§ 1.6 O produto externo" . Álgebra geométrica para físicos . Cambridge: Cambridge University Press . p. 11 e segs . ISBN 978-0-521-71595-9.