Desigualdade de meios aritméticos e geométricos - Inequality of arithmetic and geometric means

Em matemática , a desigualdade das médias aritméticas e geométricas , ou mais resumidamente a desigualdade AM-GM , afirma que a média aritmética de uma lista de números reais não negativos é maior ou igual à média geométrica da mesma lista; e, além disso, que as duas médias são iguais se e somente se todos os números da lista forem iguais (nesse caso, ambos são esse número).

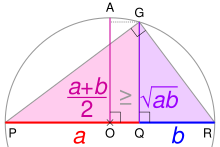
O caso não trivial mais simples - ou seja, com mais de uma variável - para dois números não negativos x e  y , é a afirmação de que

${\ displaystyle {\ frac {x + y} {2}} \ geq {\ sqrt {xy}}}$

com igualdade se e somente se x = y . Este caso pode ser visto pelo fato de que o quadrado de um número real é sempre não negativo (maior ou igual a zero) e do caso elementar ( a ± b ) ² = a ² ± 2 ab + b ² do fórmula binomial :

${\ displaystyle {\ begin {alinhados} 0 & \ leq (xy) ^ {2} \\ & = x ^ {2} -2xy + y ^ {2} \\ & = x ^ {2} + 2xy + y ^ {2} -4xy \\ & = (x + y) ^ {2} -4xy. \ End {alinhado}}}$

Portanto, ( x + y ) ² ≥ 4 xy , com igualdade precisamente quando ( x - y ) ² = 0 , ou seja, x = y . A desigualdade AM-GM segue então tirando a raiz quadrada positiva de ambos os lados e dividindo ambos os lados por 2 .

Para obter uma interpretação geométrica, considere um rectângulo com lados de comprimento  x e  y , portanto, tem perímetro 2 x + 2 y e área  xy . Da mesma forma, um quadrado com todos os lados de comprimento √ xy tem o perímetro 4 √ xy e a mesma área do retângulo. O caso não trivial mais simples da desigualdade AM-GM implica para os perímetros que 2 x + 2 y ≥ 4 √ xy e que apenas o quadrado tem o menor perímetro entre todos os retângulos de área igual.

Extensões da desigualdade AM-GM estão disponíveis para incluir pesos ou médias generalizadas .

Fundo

A média aritmética , ou menos precisamente a média , de uma lista de n números x ₁ , x ₂ ,. . . , x _n é a soma dos números dividida por  n :

${\ displaystyle {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n}} {n}}.}$

A média geométrica é semelhante, exceto que é definida apenas para uma lista de números reais não negativos e usa multiplicação e uma raiz no lugar de adição e divisão:

${\ displaystyle {\ sqrt [{n}] {x_ {1} \ cdot x_ {2} \ cdots x_ {n}}}.}$

Se x ₁ , x ₂ ,. . . , x _n > 0 , isso é igual ao exponencial da média aritmética dos logaritmos naturais dos números:

${\ displaystyle \ exp \ left ({\ frac {\ ln {x_ {1}} + \ ln {x_ {2}} + \ cdots + \ ln {x_ {n}}} {n}} \ right). }$

A desigualdade

Reafirmando a desigualdade usando notação matemática, temos isso para qualquer lista de n números reais não negativos x ₁ , x ₂ ,. . . , x _n ,

${\ displaystyle {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n}} {n}} \ geq {\ sqrt [{n}] {x_ {1} \ cdot x_ {2} \ cdots x_ {n}}} \ ,,}$

e essa igualdade é válida se e somente se x ₁ = x ₂ = · · · = x _n .

Interpretação geométrica

Em duas dimensões, 2 x ₁ + 2 x ₂ é o perímetro de um retângulo com lados de comprimento  x ₁ e  x ₂ . Da mesma forma, 4 √ x ₁ x ₂ é o perímetro de um quadrado com a mesma área , x ₁ x ₂ , desse retângulo. Assim, para n = 2, a desigualdade AM-GM afirma que um retângulo de uma determinada área tem o menor perímetro se esse retângulo também for um quadrado.

A desigualdade total é uma extensão dessa ideia para n dimensões. Cada vértice de uma caixa n- dimensional está conectado a n arestas. Se os comprimentos dessas arestas forem x ₁ , x ₂ ,. . . , x _n , então x ₁ + x ₂ + · · · + x _n é o comprimento total das arestas incidentes ao vértice. Existem 2 ⁿ vértices, então multiplicamos isso por  2 ⁿ ; uma vez que cada aresta, no entanto, encontra dois vértices, cada aresta é contada duas vezes. Portanto, dividimos por  2 e concluímos que existem 2 ^{n −1} n arestas. Existem igualmente muitas arestas de cada comprimento e n comprimentos; portanto, há 2 ^{n −1} arestas de cada comprimento e o total de todos os comprimentos das arestas é 2 ^{n −1} ( x ₁ + x ₂ + · · · + x _n ) . Por outro lado,

${\ displaystyle 2 ^ {n-1} (x_ {1} + \ ldots + x_ {n}) = 2 ^ {n-1} n {\ sqrt [{n}] {x_ {1} x_ {2} \ cdots x_ {n}}}}$

é o comprimento total das arestas conectadas a um vértice em um cubo n- dimensional de igual volume, pois neste caso x ₁ = ... = x _n . Já que a desigualdade diz

${\ displaystyle {x_ {1} + x_ {2} + \ cdots + x_ {n} \ over n} \ geq {\ sqrt [{n}] {x_ {1} x_ {2} \ cdots x_ {n} }},}$

pode ser reapresentado multiplicando por n 2 ^{n -1} para obter

${\ displaystyle 2 ^ {n-1} (x_ {1} + x_ {2} + \ cdots + x_ {n}) \ geq 2 ^ {n-1} n {\ sqrt [{n}] {x_ { 1} x_ {2} \ cdots x_ {n}}}}$

com igualdade se e somente se x ₁ = x ₂ = · · · = x _n .

Assim, a desigualdade AM-GM afirma que apenas o n- cubo tem a menor soma dos comprimentos das arestas conectadas a cada vértice entre todas as caixas n- dimensionais com o mesmo volume.

Aplicação de exemplo

Considere a função

${\ displaystyle f (x, y, z) = {\ frac {x} {y}} + {\ sqrt {\ frac {y} {z}}} + {\ sqrt [{3}] {\ frac { z} {x}}}}$

para todos os números reais positivos x , y e  z . Suponha que desejamos encontrar o valor mínimo desta função. Pode ser reescrito como:

${\ displaystyle {\ begin {align} f (x, y, z) & = 6 \ cdot {\ frac {{\ frac {x} {y}} + {\ frac {1} {2}} {\ sqrt {\ frac {y} {z}}} + {\ frac {1} {2}} {\ sqrt {\ frac {y} {z}}} + {\ frac {1} {3}} {\ sqrt [{3}] {\ frac {z} {x}}} + {\ frac {1} {3}} {\ sqrt [{3}] {\ frac {z} {x}}} + {\ frac {1} {3}} {\ sqrt [{3}] {\ frac {z} {x}}}} {6}} \\ & = 6 \ cdot {\ frac {x_ {1} + x_ {2 } + x_ {3} + x_ {4} + x_ {5} + x_ {6}} {6}} \ end {alinhado}}}$

com

${\ displaystyle x_ {1} = {\ frac {x} {y}}, \ qquad x_ {2} = x_ {3} = {\ frac {1} {2}} {\ sqrt {\ frac {y} {z}}}, \ qquad x_ {4} = x_ {5} = x_ {6} = {\ frac {1} {3}} {\ sqrt [{3}] {\ frac {z} {x} }}.}$

Aplicando a desigualdade AM-GM para n = 6 , obtemos

${\ displaystyle {\ begin {alinhados} f (x, y, z) & \ geq 6 \ cdot {\ sqrt [{6}] {{\ frac {x} {y}} \ cdot {\ frac {1} {2}} {\ sqrt {\ frac {y} {z}}} \ cdot {\ frac {1} {2}} {\ sqrt {\ frac {y} {z}}} \ cdot {\ frac { 1} {3}} {\ sqrt [{3}] {\ frac {z} {x}}} \ cdot {\ frac {1} {3}} {\ sqrt [{3}] {\ frac {z } {x}}} \ cdot {\ frac {1} {3}} {\ sqrt [{3}] {\ frac {z} {x}}}}} \\ & = 6 \ cdot {\ sqrt [ {6}] {{\ frac {1} {2 \ cdot 2 \ cdot 3 \ cdot 3 \ cdot 3}} {\ frac {x} {y}} {\ frac {y} {z}} {\ frac {z} {x}}}} \\ & = 2 ^ {2/3} \ cdot 3 ^ {1/2}. \ end {alinhado}}}$

Além disso, sabemos que os dois lados são iguais exatamente quando todos os termos da média são iguais:

${\ displaystyle f (x, y, z) = 2 ^ {2/3} \ cdot 3 ^ {1/2} \ quad {\ mbox {quando}} \ quad {\ frac {x} {y}} = {\ frac {1} {2}} {\ sqrt {\ frac {y} {z}}} = {\ frac {1} {3}} {\ sqrt [{3}] {\ frac {z} { x}}}.}$

Todos os pontos ( x , y , z ) que satisfazem essas condições estão em uma meia-linha começando na origem e são dados por

${\ displaystyle (x, y, z) = {\ biggr (} t, {\ sqrt [{3}] {2}} {\ sqrt {3}} \, t, {\ frac {3 {\ sqrt { 3}}} {2}} \, t {\ biggr)} \ quad {\ mbox {com}} \ quad t> 0.}$

Aplicações práticas

Uma aplicação prática importante em matemática financeira é calcular a taxa de retorno : o retorno anualizado , calculado por meio da média geométrica, é menor que o retorno anual médio, calculado pela média aritmética (ou igual se todos os retornos forem iguais). Isso é importante na análise de investimentos , pois o retorno médio superestima o efeito cumulativo.

Provas da desigualdade AM-GM

Prova usando a desigualdade de Jensen

A desigualdade de Jensen afirma que o valor de uma função côncava de uma média aritmética é maior ou igual à média aritmética dos valores da função. Uma vez que a função logaritmo é côncava, temos

${\ displaystyle \ log \ left ({\ frac {\ sum _ {i} x_ {i}} {n}} \ right) \ geq \ sum {\ frac {1} {n}} \ log x_ {i} = \ sum \ left (\ log x_ {i} ^ {1 / n} \ right) = \ log \ left (\ prod x_ {i} ^ {1 / n} \ right).}$

Pegando anti-registros da extrema esquerda e extrema direita, temos a desigualdade AM – GM.

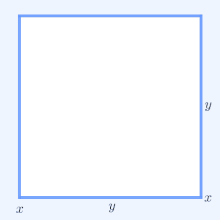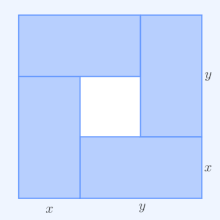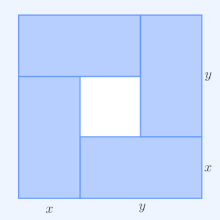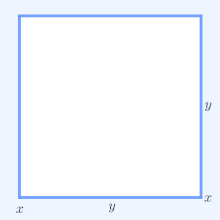
Prova pela média da média aritmética

Temos que mostrar isso

${\ displaystyle {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n}} {n}} \ geq {\ sqrt [{n}] {x_ {1} x_ {2} \ cdots x_ {n}}}}$

com igualdade apenas quando todos os números são iguais. Se x _i ≠ x _j , então substituir x _i e x _j por ( x _i + x _j ) / 2 deixará a média aritmética no lado esquerdo inalterada, mas aumentará a média geométrica no lado direito Porque

${\ displaystyle {\ Bigl (} {\ frac {x_ {i} + x_ {j}} {2}} {\ Bigr)} ^ {2} -x_ {i} x_ {j} = {\ Bigl (} {\ frac {x_ {i} -x_ {j}} {2}} {\ Bigr)} ^ {2}> 0.}$

Assim, o lado direito será maior quando todos os x _i s forem iguais à média aritmética

${\ displaystyle \ alpha = {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n}} {n}},}$

assim, como este é o maior valor do lado direito da expressão, temos

${\ displaystyle {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n}} {n}} = \ alpha = {\ sqrt [{n}] {\ alpha \ alpha \ cdots \ alpha }} \ geq {\ sqrt [{n}] {x_ {1} x_ {2} \ cdots x_ {n}}}.}$

Esta é uma prova válida para o caso n = 2 , mas o procedimento de tomar médias de pares iterativamente pode falhar em produzir n números iguais no caso n ≥ 3 . Um exemplo desse caso é x ₁ = x ₂ ≠ x ₃ : a média de dois números diferentes produz dois números iguais, mas o terceiro ainda é diferente. Portanto, nunca realmente obtemos uma desigualdade envolvendo a média geométrica de três números iguais.

No caso geral, o processo de cálculo da média acima tende a números iguais e, portanto, prova o AM-GM.

Podemos ver isso observando que um de é negativo e que, se for a média de todos os números, podemos medir a variância considerando . Este termo é sempre positivo e tende a zero na transformação : ${\ displaystyle x_ {i}, x_ {j}}$${\ displaystyle \ alpha}$${\ displaystyle n}$${\ displaystyle (x_ {i} - \ alpha) ^ {2} + (x_ {j} - \ alpha) ^ {2}}$${\ displaystyle x_ {i}, x_ {j} \ to {\ frac {x_ {i} + x_ {j}} {2}}}$

Vamos, WLOG , e . ${\ displaystyle d_ {i} = x_ {i} - \ alpha> 0}$${\ displaystyle d_ {j} = x_ {j} - \ alpha <0}$

Então

${\ displaystyle 2 \ left ({\ frac {x_ {i} + x_ {j}} {2}} - \ alpha \ right) ^ {2}}$

${\ displaystyle = 2 \ left ({\ frac {x_ {i} - \ alpha} {2}} + {\ frac {x_ {j} - \ alpha} {2}} \ right) ^ {2}}$

${\ displaystyle = 2 \ left ({\ frac {d_ {i}} {2}} + {\ frac {d_ {j}} {2}} \ right) ^ {2}}$

${\ displaystyle = {\ frac {d_ {i} ^ {2}} {2}} + {\ frac {d_ {j} ^ {2}} {2}} - d_ {i} | d_ {j} | }$

${\ displaystyle \ leq {\ frac {d_ {i} ^ {2} + d_ {j} ^ {2}} {2}}}$

Provas de indução

Prova por indução # 1

Dos números reais não negativos x ₁ ,. . . , x _n , a instrução AM-GM é equivalente a

${\ displaystyle \ alpha ^ {n} \ geq x_ {1} x_ {2} \ cdots x_ {n}}$

com igualdade se e somente se α = x _i para todo i ∈ {1,. . . , n } .

Para a prova a seguir, aplicamos indução matemática e apenas regras bem conhecidas da aritmética.

Base de indução: para n = 1, a afirmação é verdadeira com igualdade.

Hipótese de indução: Suponha que a instrução AM-GM seja válida para todas as opções de n números reais não negativos.

Etapa de indução: Considere n + 1 números reais não negativos x ₁ ,. . . , x _{n +1} ,. Sua média aritmética α satisfaz

${\ displaystyle (n + 1) \ alpha = \ x_ {1} + \ cdots + x_ {n} + x_ {n + 1}.}$

Se todos os x _i forem iguais a α , então temos igualdade na instrução AM – GM e pronto. No caso em que alguns não são iguais a α , deve existir um número maior que a média aritmética α e outro menor que α . Sem perda de generalidade, podemos reordenar nosso x _i para colocar esses dois elementos particulares no final: x _n > α e x _{n +1} < α . Então

${\ displaystyle x_ {n} - \ alpha> 0 \ qquad \ alpha -x_ {n + 1}> 0}$

${\ displaystyle \ implica (x_ {n} - \ alpha) (\ alpha -x_ {n + 1})> 0 \,. \ qquad (*)}$

Agora defina y com

${\ displaystyle y: = x_ {n} + x_ {n + 1} - \ alpha \ geq x_ {n} - \ alpha> 0 \ ,,}$

e considere os n números x ₁ ,. . . , x _{n –1} , y que são todos não negativos. Desde a

${\ displaystyle (n + 1) \ alpha = x_ {1} + \ cdots + x_ {n-1} + x_ {n} + x_ {n + 1}}$

${\ displaystyle n \ alpha = x_ {1} + \ cdots + x_ {n-1} + \ underbrace {x_ {n} + x_ {n + 1} - \ alpha} _ {= \, y},}$

Assim, α é também a média aritmética de n números x ₁ ,. . . , x _{n -1} , y e a hipótese de indução implica

${\ displaystyle \ alpha ^ {n + 1} = \ alpha ^ {n} \ cdot \ alpha \ geq x_ {1} x_ {2} \ cdots x_ {n-1} y \ cdot \ alpha. \ qquad (* *)}$

Devido a (*) sabemos que

${\ displaystyle (\ underbrace {x_ {n} + x_ {n + 1} - \ alpha} _ {= \, y}) \ alpha -x_ {n} x_ {n + 1} = (x_ {n} - \ alpha) (\ alpha -x_ {n + 1})> 0,}$

portanto

${\ displaystyle y \ alpha> x_ {n} x_ {n + 1} \ ,, \ qquad ({*} {*} {*})}$

em particular α > 0 . Portanto, se pelo menos um dos números x ₁ ,. . . , x _{n –1} é zero, então já temos desigualdade estrita em (**). Caso contrário, o lado direito de (**) é positivo e a desigualdade estrita é obtida usando a estimativa (***) para obter um limite inferior do lado direito de (**). Assim, em ambos os casos, podemos substituir (***) por (**) para obter

${\ displaystyle \ alpha ^ {n + 1}> x_ {1} x_ {2} \ cdots x_ {n-1} x_ {n} x_ {n + 1} \ ,,}$

que completa a prova.

Prova por indução # 2

Em primeiro lugar, devemos provar que para números reais x ₁ <1 e x ₂ > 1 segue-se

${\ displaystyle x_ {1} + x_ {2}> x_ {1} x_ {2} +1.}$

Na verdade, multiplicando ambos os lados da inequação x ₂ > 1 por 1 - x ₁ , dá

${\ displaystyle x_ {2} -x_ {1} x_ {2}> 1-x_ {1},}$

de onde a desigualdade exigida é obtida imediatamente.

Agora, vamos provar que, para números reais positivos x ₁ ,. . . , x _n satisfazendo x ₁ . . . x _n = 1 , existe

${\ displaystyle x_ {1} + \ cdots + x_ {n} \ geq n.}$

A igualdade é válida apenas se x ₁ = ... = x _n = 1 .

Base de indução: para n = 2, a afirmação é verdadeira devido à propriedade acima.

Hipótese de indução: suponha que a afirmação seja verdadeira para todos os números naturais até n - 1 .

Etapa de indução: Considere o número natural n , ou seja, para números reais positivos x ₁ ,. . . , x _n , contém x ₁ . . . x _n = 1 . Existe pelo menos um x _k <1 , então deve haver pelo menos um x _j > 1 . Sem perda de generalidade, consideramos k = n - 1 e j = n .

Além disso, a igualdade x ₁ . . . x _n = 1 escreveremos na forma de ( x ₁ ... x _{n –2} ) ( x _{n –1} x _n ) = 1 . Então, a hipótese de indução implica

${\ displaystyle (x_ {1} + \ cdots + x_ {n-2}) + (x_ {n-1} x_ {n})> n-1.}$

No entanto, levando em consideração a base de indução, temos

${\ displaystyle {\ begin {alinhado} x_ {1} + \ cdots + x_ {n-2} + x_ {n-1} + x_ {n} & = (x_ {1} + \ cdots + x_ {n- 2}) + (x_ {n-1} + x_ {n}) \\ &> (x_ {1} + \ cdots + x_ {n-2}) + x_ {n-1} x_ {n} +1 \\ &> n, \ end {alinhado}}}$

que completa a prova.

Para números reais positivos, a ₁ ,. . . , a _n , vamos denotar

${\ displaystyle x_ {1} = {\ frac {a_ {1}} {\ sqrt [{n}] {a_ {1} \ cdots a_ {n}}}}, ..., x_ {n} = { \ frac {a_ {n}} {\ sqrt [{n}] {a_ {1} \ cdots a_ {n}}}}.}$

Os números x ₁ ,. . . , x _n satisfaz a condição x ₁ . . . x _n = 1 . Então nós temos

${\ displaystyle {\ frac {a_ {1}} {\ sqrt [{n}] {a_ {1} \ cdots a_ {n}}}} + \ cdots + {\ frac {a_ {n}} {\ sqrt [{n}] {a_ {1} \ cdots a_ {n}}}} \ geq n,}$

de onde obtemos

${\ displaystyle {\ frac {a_ {1} + \ cdots + a_ {n}} {n}} \ geq {\ sqrt [{n}] {a_ {1} \ cdots a_ {n}}},}$

com a igualdade valendo apenas para a ₁ = ... = a _n .

Prova de Cauchy usando indução para frente e para trás

A seguinte prova por casos depende diretamente de regras bem conhecidas da aritmética, mas emprega a técnica raramente usada de indução para frente e para trás. É essencialmente de Augustin Louis Cauchy e pode ser encontrado em seu Cours d'analyse .

O caso em que todos os termos são iguais

Se todos os termos forem iguais:

${\ displaystyle x_ {1} = x_ {2} = \ cdots = x_ {n},}$

então sua soma é nx ₁ , então sua média aritmética é  x ₁ ; e seu produto é x ₁ ⁿ , então sua média geométrica é  x ₁ ; portanto, a média aritmética e a média geométrica são iguais, conforme desejado.

O caso em que nem todos os termos são iguais

Resta mostrar que, se nem todos os termos são iguais, então a média aritmética é maior do que a média geométrica. Claramente, isso só é possível quando n > 1 .

Este caso é significativamente mais complexo e o dividimos em subcasos.

O subcaso onde n = 2

Se N = 2 , em seguida, temos dois termos, x ₁ e x ₂ , e uma vez que (por nossa suposição) nem todos os termos são iguais, tem-se:

${\ displaystyle {\ begin {align} {\ Bigl (} {\ frac {x_ {1} + x_ {2}} {2}} {\ Bigr)} ^ {2} -x_ {1} x_ {2} & = {\ frac {1} {4}} (x_ {1} ^ {2} + 2x_ {1} x_ {2} + x_ {2} ^ {2}) - x_ {1} x_ {2} \ \ & = {\ frac {1} {4}} (x_ {1} ^ {2} -2x_ {1} x_ {2} + x_ {2} ^ {2}) \\ & = {\ Bigl (} {\ frac {x_ {1} -x_ {2}} {2}} {\ Bigr)} ^ {2}> 0, \ end {alinhado}}}$

portanto

${\ displaystyle {\ frac {x_ {1} + x_ {2}} {2}} \ geq {\ sqrt {x_ {1} x_ {2}}}}$

como desejado.

O subcaso onde n = 2 ^k

Considere o caso em que n = 2 ^k , onde k é um número inteiro positivo. Procedemos por indução matemática.

No caso base, k = 1 , então n = 2 . Já mostramos que a desigualdade se mantém quando n = 2 , então terminamos.

Agora, suponha que para um dado k > 1 , já mostramos que a desigualdade é válida para n = 2 ^{k −1} e queremos mostrar que ela é válida para n = 2 ^k . Para fazer isso, aplicamos a desigualdade duas vezes para 2 ^{k -1} números e uma vez para 2 números para obter:

${\ displaystyle {\ begin {align} {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {2 ^ {k}}} {2 ^ {k}}} & {} = {\ frac {{\ frac {x_ {1} + x_ {2} + \ cdots + x_ {2 ^ {k-1}}} {2 ^ {k-1}}} + {\ frac {x_ {2 ^ {k -1} +1} + x_ {2 ^ {k-1} +2} + \ cdots + x_ {2 ^ {k}}} {2 ^ {k-1}}}} {2}} \\ [ 7pt] & \ geq {\ frac {{\ sqrt [{2 ^ {k-1}}] {x_ {1} x_ {2} \ cdots x_ {2 ^ {k-1}}}} + {\ sqrt [{2 ^ {k-1}}] {x_ {2 ^ {k-1} +1} x_ {2 ^ {k-1} +2} \ cdots x_ {2 ^ {k}}}}} { 2}} \\ [7pt] & \ geq {\ sqrt {{\ sqrt [{2 ^ {k-1}}] {x_ {1} x_ {2} \ cdots x_ {2 ^ {k-1}} }} {\ sqrt [{2 ^ {k-1}}] {x_ {2 ^ {k-1} +1} x_ {2 ^ {k-1} +2} \ cdots x_ {2 ^ {k} }}}}} \\ [7pt] & = {\ sqrt [{2 ^ {k}}] {x_ {1} x_ {2} \ cdots x_ {2 ^ {k}}}} \ end {alinhado} }}$

onde na primeira desigualdade, os dois lados são iguais apenas se

${\ displaystyle x_ {1} = x_ {2} = \ cdots = x_ {2 ^ {k-1}}}$

e

${\ displaystyle x_ {2 ^ {k-1} +1} = x_ {2 ^ {k-1} +2} = \ cdots = x_ {2 ^ {k}}}$

(neste caso, a primeira média aritmética e a primeira média geométrica são ambas iguais  ax ₁ , e de forma semelhante com a segunda média aritmética e a segunda média geométrica); e na segunda desigualdade, os dois lados só são iguais se as duas médias geométricas forem iguais. Uma vez que nem todos os números de 2 ^k são iguais, não é possível que ambas as desigualdades sejam igualdades, então sabemos que:

${\ displaystyle {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {2 ^ {k}}} {2 ^ {k}}} \ geq {\ sqrt [{2 ^ {k}} ] {x_ {1} x_ {2} \ cdots x_ {2 ^ {k}}}}}$

como desejado.

O subcaso onde n <2 ^k

Se n não é uma potência natural de  2 , então certamente é menor que alguma potência natural de 2, uma vez que a sequência 2, 4, 8,. . . , 2 ^k ,. . . é ilimitado acima. Portanto, sem perda de generalidade, seja m alguma potência natural de 2 maior que  n .

Portanto, se temos n termos, vamos denotar sua média aritmética por  α e expandir nossa lista de termos assim:

${\ displaystyle x_ {n + 1} = x_ {n + 2} = \ cdots = x_ {m} = \ alpha.}$

Então temos:

${\ displaystyle {\ begin {alinhados} \ alpha & = {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n}} {n}} \\ [6pt] & = {\ frac { {\ frac {m} {n}} \ left (x_ {1} + x_ {2} + \ cdots + x_ {n} \ right)} {m}} \\ [6pt] & = {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n} + {\ frac {(mn)} {n}} \ left (x_ {1} + x_ {2} + \ cdots + x_ {n} \ direita)} {m}} \\ [6pt] & = {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n} + \ esquerda (mn \ direita) \ alpha} {m}} \\ [6pt] & = {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n} + x_ {n + 1} + \ cdots + x_ {m}} {m}} \\ [6pt] & \ geq {\ sqrt [{m}] {x_ {1} x_ {2} \ cdots x_ {n} x_ {n + 1} \ cdots x_ {m}}} \\ [6pt] & = {\ sqrt [{m}] {x_ {1} x_ {2} \ cdots x_ {n} \ alpha ^ {mn}}} \ ,, \ end {alinhado}}}$

tão

${\ displaystyle \ alpha ^ {m} \ geq x_ {1} x_ {2} \ cdots x_ {n} \ alpha ^ {mn}}$

e

${\ displaystyle \ alpha \ geq {\ sqrt [{n}] {x_ {1} x_ {2} \ cdots x_ {n}}}}$

como desejado.

Prova por indução usando cálculo básico

A seguinte prova usa indução matemática e alguns cálculos diferenciais básicos .

Base de indução : para n = 1, a afirmação é verdadeira com igualdade.

Hipótese de indução : Suponha que a instrução AM-GM seja válida para todas as opções de n números reais não negativos.

Etapa de indução : Para provar a afirmação para n + 1 números reais não negativos x ₁ ,. . . , x _n , x _{n +1} , precisamos provar que

${\ displaystyle {\ frac {x_ {1} + \ cdots + x_ {n} + x_ {n + 1}} {n + 1}} - ({x_ {1} \ cdots x_ {n} x_ {n + 1}}) ^ {\ frac {1} {n + 1}} \ geq 0}$

com igualdade apenas se todos os n + 1 números forem iguais.

Se todos os números forem zero, a desigualdade se mantém com igualdade. Se alguns números, mas não todos, forem zero, teremos desigualdade estrita. Portanto, podemos assumir a seguir que todos os n + 1 números são positivos.

Consideramos o último número x _{n +1} como uma variável e definimos a função

${\ displaystyle f (t) = {\ frac {x_ {1} + \ cdots + x_ {n} + t} {n + 1}} - ({x_ {1} \ cdots x_ {n} t}) ^ {\ frac {1} {n + 1}}, \ qquad t> 0.}$

Provar o passo de indução é equivalente a mostrar que f ( t ) ≥ 0 para todo t > 0 , com f ( t ) = 0 apenas se x ₁ ,. . . , x _n e  t são todos iguais. Isso pode ser feito analisando os pontos críticos de  f usando alguns cálculos básicos.

A primeira derivada de f é dada por

${\ displaystyle f '(t) = {\ frac {1} {n + 1}} - {\ frac {1} {n + 1}} ({x_ {1} \ cdots x_ {n}}) ^ { \ frac {1} {n + 1}} t ^ {- {\ frac {n} {n + 1}}}, \ qquad t> 0.}$

Um ponto crítico t ₀ deve satisfazer f ′ ( t ₀ ) = 0 , o que significa

${\ displaystyle ({x_ {1} \ cdots x_ {n}}) ^ {\ frac {1} {n + 1}} t_ {0} ^ {- {\ frac {n} {n + 1}}} = 1.}$

Após uma pequena reorganização, obtemos

${\ displaystyle t_ {0} ^ {\ frac {n} {n + 1}} = ({x_ {1} \ cdots x_ {n}}) ^ {\ frac {1} {n + 1}},}$

e finalmente

${\ displaystyle t_ {0} = ({x_ {1} \ cdots x_ {n}}) ^ {\ frac {1} {n}},}$

que é a média geométrica de x ₁ ,. . . , x _n . Este é o único ponto crítico de  f . Como f ′ ′ ( t )> 0 para todo t > 0 , a função  f é estritamente convexa e tem um mínimo global estrito em  t ₀ . Em seguida, calculamos o valor da função neste mínimo global:

${\ displaystyle {\ begin {alinhados} f (t_ {0}) & = {\ frac {x_ {1} + \ cdots + x_ {n} + ({x_ {1} \ cdots x_ {n}}) ^ {1 / n}} {n + 1}} - ({x_ {1} \ cdots x_ {n}}) ^ {\ frac {1} {n + 1}} ({x_ {1} \ cdots x_ { n}}) ^ {\ frac {1} {n (n + 1)}} \\ & = {\ frac {x_ {1} + \ cdots + x_ {n}} {n + 1}} + {\ frac {1} {n + 1}} ({x_ {1} \ cdots x_ {n}}) ^ {\ frac {1} {n}} - ({x_ {1} \ cdots x_ {n}}) ^ {\ frac {1} {n}} \\ & = {\ frac {x_ {1} + \ cdots + x_ {n}} {n + 1}} - {\ frac {n} {n + 1} } ({x_ {1} \ cdots x_ {n}}) ^ {\ frac {1} {n}} \\ & = {\ frac {n} {n + 1}} {\ Bigl (} {\ frac {x_ {1} + \ cdots + x_ {n}} {n}} - ({x_ {1} \ cdots x_ {n}}) ^ {\ frac {1} {n}} {\ Bigr)} \ \ & \ geq 0, \ end {alinhado}}}$

onde a desigualdade final se mantém devido à hipótese de indução. A hipótese também diz que podemos ter igualdade apenas quando x ₁ ,. . . , x _n são todos iguais. Nesse caso, sua média geométrica   t ₀ tem o mesmo valor, Conseqüentemente, a menos que x ₁ ,. . . , x _n , x _{n +1} são todos iguais, temos f ( x _{n +1} )> 0 . Isso completa a prova.

Esta técnica pode ser usada da mesma maneira para provar a desigualdade AM-GM generalizada e a desigualdade de Cauchy-Schwarz no espaço euclidiano R ⁿ .

Prova de Pólya usando a função exponencial

George Pólya forneceu uma prova semelhante à que se segue. Seja f ( x ) = e ^{x –1} - x para todo real  x , com a primeira derivada f ′ ( x ) = e ^{x –1} - 1 e a segunda derivada f ′ ′ ( x ) = e ^{x –1} . Observe que f (1) = 0 , f ' (1) = 0 e f' ' ( x )> 0 para tudo real  x , portanto, f é estritamente convexa com o mínimo absoluto em x = 1 . Portanto, x ≤ e ^{x –1} para todo real  x com igualdade apenas para x = 1 .

Considere uma lista de números reais não negativos x ₁ , x ₂ ,. . . , x _n . Se eles forem todos zero, então a desigualdade AM – GM se mantém com igualdade. Portanto, podemos assumir o seguinte para sua média aritmética α > 0 . Pela aplicação n vezes da desigualdade acima, obtemos que

${\ displaystyle {\ begin {align} {{\ frac {x_ {1}} {\ alpha}} {\ frac {x_ {2}} {\ alpha}} \ cdots {\ frac {x_ {n}} { \ alpha}}} & \ leq {e ^ {{\ frac {x_ {1}} {\ alpha}} - 1} e ^ {{\ frac {x_ {2}} {\ alpha}} - 1} \ cdots e ^ {{\ frac {x_ {n}} {\ alpha}} - 1}} \\ & = \ exp {\ Bigl (} {\ frac {x_ {1}} {\ alpha}} - 1+ {\ frac {x_ {2}} {\ alpha}} - 1+ \ cdots + {\ frac {x_ {n}} {\ alpha}} - 1 {\ Bigr)}, \ qquad (*) \ end { alinhado}}}$

com igualdade se e somente se x _i = α para todo i ∈ {1,. . . , n } . O argumento da função exponencial pode ser simplificado:

${\ displaystyle {\ begin {align} {\ frac {x_ {1}} {\ alpha}} - 1 + {\ frac {x_ {2}} {\ alpha}} - 1+ \ cdots + {\ frac { x_ {n}} {\ alpha}} - 1 & = {\ frac {x_ {1} + x_ {2} + \ cdots + x_ {n}} {\ alpha}} - n \\ & = {\ frac { n \ alpha} {\ alpha}} - n \\ & = 0. \ end {alinhado}}}$

Voltando a (*) ,

${\ displaystyle {\ frac {x_ {1} x_ {2} \ cdots x_ {n}} {\ alpha ^ {n}}} \ leq e ^ {0} = 1,}$

que produz x ₁ x ₂ · · · x _n ≤ α ⁿ , daí o resultado

${\ displaystyle {\ sqrt [{n}] {x_ {1} x_ {2} \ cdots x_ {n}}} \ leq \ alpha.}$

Prova por Multiplicadores Lagrangianos

Se algum deles for , não há nada a provar. Portanto, podemos assumir que todos os são estritamente positivos. ${\ displaystyle x_ {i}}$${\ displaystyle 0}$${\ displaystyle x_ {i}}$

Como as médias aritméticas e geométricas são homogêneas de grau 1, sem perda de generalidade assuma isso . Definir e . A desigualdade será provada (junto com o caso de igualdade) se pudermos mostrar que o mínimo de sujeito à restrição é igual a , e o mínimo só é alcançado quando . Vamos primeiro mostrar que o problema de minimização restrita tem um mínimo global. ${\ displaystyle \ prod _ {i = 1} ^ {n} x_ {i} = 1}$${\ displaystyle G (x_ {1}, x_ {2}, \ ldots, x_ {n}) = \ prod _ {i = 1} ^ {n} x_ {i}}$${\ displaystyle F (x_ {1}, x_ {2}, \ ldots, x_ {n}) = {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} x_ {i} }$${\ displaystyle F (x_ {1}, x_ {2}, ..., x_ {n}),}$${\ displaystyle G (x_ {1}, x_ {2}, \ ldots, x_ {n}) = 1,}$${\ displaystyle 1}$${\ displaystyle x_ {1} = x_ {2} = \ cdots = x_ {n} = 1}$

Definir . Como a interseção é compacta, o teorema do valor extremo garante que o mínimo de sujeito às restrições e seja atingido em algum ponto interno . Por outro lado, observe que se algum dos , then , while e . Isso significa que o mínimo dentro é de fato um mínimo global, uma vez que o valor de em qualquer ponto interno certamente não é menor que o mínimo, e o valor de em qualquer ponto externo é estritamente maior do que o valor em , que não é menor do que o mínimo. ${\ displaystyle K = \ {(x_ {1}, x_ {2}, \ ldots, x_ {n}) \ dois pontos 0 \ leq x_ {1}, x_ {2}, \ ldots, x_ {n} \ leq n \}}$${\ displaystyle K \ cap \ {G = 1 \}}$${\ displaystyle F (x_ {1}, x_ {2}, ..., x_ {n})}$${\ displaystyle G (x_ {1}, x_ {2}, \ ldots, x_ {n}) = 1}$${\ displaystyle (x_ {1}, x_ {2}, \ ldots, x_ {n}) \ in K}$${\ displaystyle K}$${\ displaystyle x_ {i}> n}$${\ displaystyle F (x_ {1}, x_ {2}, \ ldots, x_ {n})> 1}$${\ displaystyle F (1,1, \ ldots, 1) = 1}$${\ displaystyle (1,1, \ ldots, 1) \ in K \ cap \ {G = 1 \}}$${\ displaystyle K \ cap \ {G = 1 \}}$${\ displaystyle F}$${\ displaystyle K \ cap \ {G = 1 \}}$${\ displaystyle F}$${\ displaystyle (y_ {1}, y_ {2}, \ ldots, y_ {n})}$${\ displaystyle K}$${\ displaystyle (1,1, \ ldots, 1)}$

O método dos multiplicadores de Lagrange diz que o mínimo global é atingido em um ponto onde o gradiente de é vezes o gradiente de , para alguns . Mostraremos que o único ponto em que isso acontece é quando e ${\ displaystyle (x_ {1}, x_ {2}, \ ldots, x_ {n})}$${\ displaystyle F (x_ {1}, x_ {2}, \ ldots, x_ {n})}$${\ displaystyle \ lambda}$${\ displaystyle G (x_ {1}, x_ {2}, \ ldots, x_ {n})}$${\ displaystyle \ lambda}$${\ displaystyle x_ {1} = x_ {2} = \ cdots = x_ {n} = 1}$${\ displaystyle F (x_ {1}, x_ {2}, ..., x_ {n}) = 1.}$

Calcular e ${\ displaystyle {\ frac {\ partial F} {\ partial x_ {i}}} = {\ frac {1} {n}}}$

${\ displaystyle {\ frac {\ partial G} {\ partial x_ {i}}} = \ prod _ {j \ neq i} x_ {j} = {\ frac {G (x_ {1}, x_ {2} , \ ldots, x_ {n})} {x_ {i}}} = {\ frac {1} {x_ {i}}}}$

ao longo da restrição. Definir os gradientes proporcionais uns aos outros, portanto, dá para cada um isso e, portanto, como o lado esquerdo não depende de , segue-se isso , e desde então , segue-se isso e , conforme desejado. ${\ displaystyle i}$${\ displaystyle {\ frac {1} {n}} = {\ frac {\ lambda} {x_ {i}}},}$${\ displaystyle n \ lambda = x_ {i}.}$${\ displaystyle i}$${\ displaystyle x_ {1} = x_ {2} = \ cdots = x_ {n}}$${\ displaystyle G (x_ {1}, x_ {2}, \ ldots, x_ {n}) = 1}$${\ displaystyle x_ {1} = x_ {2} = \ cdots = x_ {n} = 1}$${\ displaystyle F (x_ {1}, x_ {2}, \ ldots, x_ {n}) = 1}$

Generalizações

Desigualdade ponderada AM-GM

Há uma desigualdade semelhante para a média aritmética ponderada e a média geométrica ponderada . Especificamente, sejam os números não negativos x ₁ , x ₂ ,. . . , x _n e os pesos não negativos w ₁ , w ₂ ,. . . , W _n ser dada. Defina w = w ₁ + w ₂ + · · · + w _n . Se  w > 0 , então a desigualdade

${\ displaystyle {\ frac {w_ {1} x_ {1} + w_ {2} x_ {2} + \ cdots + w_ {n} x_ {n}} {w}} \ geq {\ sqrt [{w} ] {x_ {1} ^ {w_ {1}} x_ {2} ^ {w_ {2}} \ cdots x_ {n} ^ {w_ {n}}}}}$

vale com igualdade se e somente se todos os x _k com w _k > 0 forem iguais. Aqui, a convenção 0 ⁰ = 1 é usada.

Se todo w _k = 1 , isso se reduz à desigualdade acima de médias aritméticas e geométricas.

Prova usando a desigualdade de Jensen

Usando a forma finita da desigualdade de Jensen para o logaritmo natural , podemos provar a desigualdade entre a média aritmética ponderada e a média geométrica ponderada declarada acima.

Como an x _k com peso w _k = 0 não tem influência na desigualdade, podemos assumir a seguir que todos os pesos são positivos. Se todos os x _k forem iguais, a igualdade será mantida. Portanto, resta provar a desigualdade estrita se eles não forem todos iguais, o que assumiremos a seguir também. Se pelo menos um x _k é zero (mas não todos), então a média geométrica ponderada é zero, enquanto a média aritmética ponderada é positiva, portanto, a desigualdade estrita se mantém. Portanto, podemos assumir também que todos os x _k são positivos.

Uma vez que o logaritmo natural é estritamente côncavo , a forma finita da desigualdade de Jensen e as equações funcionais do logaritmo natural implicam

${\ displaystyle {\ begin {alinhado} \ ln {\ Bigl (} {\ frac {w_ {1} x_ {1} + \ cdots + w_ {n} x_ {n}} {w}} {\ Bigr)} &> {\ frac {w_ {1}} {w}} \ ln x_ {1} + \ cdots + {\ frac {w_ {n}} {w}} \ ln x_ {n} \\ & = \ ln {\ sqrt [{w}] {x_ {1} ^ {w_ {1}} x_ {2} ^ {w_ {2}} \ cdots x_ {n} ^ {w_ {n}}}}. \ end { alinhado}}}$

Uma vez que o logaritmo natural está aumentando estritamente ,

${\ displaystyle {\ frac {w_ {1} x_ {1} + \ cdots + w_ {n} x_ {n}} {w}}> {\ sqrt [{w}] {x_ {1} ^ {w_ { 1}} x_ {2} ^ {w_ {2}} \ cdots x_ {n} ^ {w_ {n}}}}.}$

Matriz Aritmética Geométrica Desigualdade Média

A maioria das generalizações de matriz da desigualdade média geométrica aritmética se aplica ao nível de normas invariantes unitariamente, devido ao fato de que mesmo se as matrizes e forem semidefinidas positivas, a matriz pode não ser semidefinida positiva e, portanto, não pode ter um quadrado canônico raiz. Em Bhatia e Kittaneh provou que para qualquer norma invariante unitariamente e matrizes semi-definidas positivas e é o caso que ${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle AB}$${\ displaystyle ||| \ cdot |||}$${\ displaystyle A}$${\ displaystyle B}$

${\ displaystyle ||| AB ||| \ leq {\ frac {1} {2}} ||| A ^ {2} + B ^ {2} |||}$

Posteriormente, nos mesmos autores comprovou-se a maior desigualdade que

${\ displaystyle ||| AB ||| \ leq {\ frac {1} {4}} ||| (A + B) ^ {2} |||}$

Finalmente, é conhecido por dimensão que a seguinte generalização de matriz mais forte possível da desigualdade média aritmético-geométrica é válida, e conjectura-se que é válida para todos${\ displaystyle n = 2}$${\ displaystyle n}$

${\ displaystyle ||| (AB) ^ {\ frac {1} {2}} ||| \ leq {\ frac {1} {2}} ||| A + B |||}$

Essa conjectura de desigualdade foi mostrada por Stephen Drury em 2012. Na verdade, ele provou

${\ displaystyle {\ sqrt {\ sigma _ {j} (AB)}} \ leq {\ frac {1} {2}} \ lambda _ {j} (A + B), \ j = 1, \ ldots, n.}$

SW Drury, On a question of Bhatia and Kittaneh, Linear Algebra Appl. 437 (2012) 1955–1960.

Outras generalizações

Outras generalizações da desigualdade de meios aritméticos e geométricos incluem:

• A desigualdade de Muirhead ,
• A desigualdade de Maclaurin ,
• Desigualdade média generalizada ,
• Meios de números complexos .

Veja também

• O quebra-cabeça da embalagem de Hoffman
• Desigualdade de Ky Fan
• Desigualdade de Young para produtos

Referências

links externos

• Arthur Lohwater (1982). “Introdução às Desigualdades” . E-book online em formato PDF.