Limite (teoria da categoria) - Limit (category theory)

Na teoria das categorias , um ramo da matemática , a noção abstrata de limite captura as propriedades essenciais das construções universais, como produtos , retrocessos e limites inversos . A dupla noção de colimite generaliza construções como uniões disjuntas , somas diretas , coprodutos , pushouts e limites diretos .

Limites e colimitos, como as noções fortemente relacionadas de propriedades universais e functores adjuntos , existem em um alto nível de abstração. Para entendê-los, é útil primeiro estudar os exemplos específicos que esses conceitos devem generalizar.

Definição

Limites e colimitos em uma categoria são definidos por meio de diagramas em . Formalmente, um diagrama de forma em é um functor de para : ${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle J}$${\ displaystyle C}$${\ displaystyle J}$${\ displaystyle C}$

${\ displaystyle F: J \ a C.}$

A categoria é pensado como uma categoria de índice , e o diagrama é pensado como indexação de um conjunto de objectos e morphisms em modelado em . ${\ displaystyle J}$${\ displaystyle F}$${\ displaystyle C}$${\ displaystyle J}$

Freqüentemente, está interessado no caso em que a categoria é uma categoria pequena ou mesmo finita . Um diagrama é considerado pequeno ou finito, sempre que for. ${\ displaystyle J}$${\ displaystyle J}$

Limites

Let Ser um diagrama de forma em uma categoria . Um cone a é um objeto de juntamente com uma família de morfismos indexados pelos objetos de , de modo que para cada morfismo em , temos . ${\ displaystyle F: J \ a C}$${\ displaystyle J}$${\ displaystyle C}$${\ displaystyle F}$${\ displaystyle N}$${\ displaystyle C}$${\ displaystyle \ psi _ {X}: N \ a F (X)}$${\ displaystyle X}$${\ displaystyle J}$${\ displaystyle f: X \ a Y}$${\ displaystyle J}$${\ displaystyle F (f) \ circ \ psi _ {X} = \ psi _ {Y}}$

Um limite do diagrama está um cone de tal modo que para todos os outros cone para existe um único morfismo de tal modo que para todos em . ${\ displaystyle F: J \ a C}$${\ displaystyle (L, \ phi)}$${\ displaystyle F}$${\ displaystyle (N, \ psi)}$${\ displaystyle F}$${\ displaystyle u: N \ a L}$${\ displaystyle \ phi _ {X} \ circ u = \ psi _ {X}}$${\ displaystyle X}$${\ displaystyle J}$

Diz-se que o cone fatora através do cone com a única fatoração . O morfismo é às vezes chamado de morfismo mediador . ${\ displaystyle (N, \ psi)}$${\ displaystyle (L, \ phi)}$${\ displaystyle u}$${\ displaystyle u}$

Os limites também são chamados de cones universais , uma vez que são caracterizados por uma propriedade universal (veja mais informações abaixo). Como acontece com toda propriedade universal, a definição acima descreve um estado equilibrado de generalidade: O objeto limite deve ser geral o suficiente para permitir que qualquer outro cone passe por ele; por outro lado, deve ser suficientemente específico, de modo que apenas uma dessas fatorações seja possível para cada cone. ${\ displaystyle L}$${\ displaystyle L}$

Limites também podem ser caracterizados como objectos terminais na categoria de cones para F .

É possível que um diagrama não tenha limite algum. No entanto, se um diagrama tem um limite, então esse limite é essencialmente único: é único até um isomorfismo único . Por esta razão, muitas vezes se fala do limite de F .

Colimits

As noções duais de limites e cones são colimites e co-cones. Embora seja simples obter as definições deles invertendo todos os morfismos nas definições acima, iremos declará-los explicitamente aqui:

Um co-cone de um diagrama é um objecto do conjunto com uma família de morphisms ${\ displaystyle F: J \ a C}$${\ displaystyle N}$${\ displaystyle C}$

${\ displaystyle \ psi _ {X}: F (X) \ a N}$

para cada objeto de , de modo que para cada morfismo em , temos . ${\ displaystyle X}$${\ displaystyle J}$${\ displaystyle f: X \ a Y}$${\ displaystyle J}$${\ displaystyle \ psi _ {Y} \ circ F (f) = \ psi _ {X}}$

Um colimite de um diagrama é um co-cone de tal que para qualquer outro co-cone de existe um morfismo único tal que para todos em . ${\ displaystyle F: J \ a C}$${\ displaystyle (L, \ phi)}$${\ displaystyle F}$${\ displaystyle (N, \ psi)}$${\ displaystyle F}$${\ displaystyle u: L \ to N}$${\ displaystyle u \ circ \ phi _ {X} = \ psi _ {X}}$${\ displaystyle X}$${\ displaystyle J}$

Os colimites também são chamados de co-cones universais . Eles podem ser caracterizados como objetos iniciais na categoria de co-cones de . ${\ displaystyle F}$

Tal como acontece com os limites, se um diagrama tem um colimite, então este colimito é único até um isomorfismo único. ${\ displaystyle F}$

Variações

Limites e colimites também podem ser definidos para coleções de objetos e morfismos sem o uso de diagramas. As definições são as mesmas (observe que nas definições acima nunca precisamos usar composição de morfismos em ). Essa variação, no entanto, não adiciona nenhuma informação nova. Qualquer coleção de objetos e morfismos define um gráfico direcionado (possivelmente grande) . Se deixarmos ser a categoria livre gerada por , existe um diagrama universal cuja imagem contém . O limite (ou colimite) deste diagrama é o mesmo que o limite (ou colimite) da coleção original de objetos e morfismos. ${\ displaystyle J}$ ${\ displaystyle G}$${\ displaystyle J}$${\ displaystyle G}$${\ displaystyle F: J \ a C}$${\ displaystyle G}$

Limite fraco e colimites fracos são definidos como limites e colimitos, exceto que a propriedade de unicidade do morfismo mediador é descartada.

Exemplos

Limites

A definição de limites é geral o suficiente para incluir várias construções úteis em ambientes práticos. No que se segue, vamos considerar o limite ( L , φ ) de um diagrama F  : J → C .

• Objetos terminais . Se J é a categoria vazia, há apenas um diagrama de forma J : o vazio (semelhante à função vazia na teoria dos conjuntos). Um cone com o diagrama de vazio é, essencialmente, apenas um objecto de C . O limite de F é qualquer objeto fatorado exclusivamente por todos os outros objetos. Esta é apenas a definição de um objeto terminal .
• Produtos . Se J é uma categoria distinta , em seguida, um diagrama F é essencialmente nada mas uma família de objectos de C , indexados por J . O limite L de F é chamado de produto desses objetos. O cone φ consiste em uma família de morfismos φ _X  : L → F ( X ) chamados de projeções do produto. Na categoria de conjuntos , por exemplo, os produtos são dados por produtos cartesianos e as projeções são apenas as projeções naturais sobre os vários fatores.
  • Poderes . Um caso especial de um produto é, quando o diagrama F é um functor constante para um objecto X de C . O limite deste diagrama é chamado o J ^th poder de X e denotado X ^J .
• Equalizadores . Se J é uma categoria com dois objectos e dois morphisms paralelas a partir de um objecto para o outro, em seguida, um diagrama de forma de J é um par de morphisms paralelas em C . O limite L de tal diagrama é chamado de equalizador desses morfismos.
  • Kernels . Um kernel é um caso especial de um equalizador onde um dos morfismos é um morfismo zero .
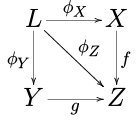
• Retrações . Vamos F ser um diagrama que escolhe três objectos X , Y , e Z em C , onde as morphisms único não-identidade são f  : X → Z e g  : Y → Z . O limite L de F é chamado de recuo ou produto de fibra . Ele pode ser bem visualizado como um quadrado comutativo :

• Limites inversos . Seja J um conjunto direcionado (considerado como uma pequena categoria pela adição de setas i → j se e somente se i ≥ j ) e seja F  : J ^op → C um diagrama. O limite de F é chamado (confusamente) de limite inverso ou limite projetivo .
• Se J = 1 , a categoria com um único objecto e morfismo, em seguida, um diagrama de forma de J é, essencialmente, apenas um objecto X de C . Um cone para um objeto X é apenas uma morphism com codomain X . Um morfismo f  : Y → X é um limite do diagrama X se e somente se f for um isomorfismo . Mais geralmente, se J for qualquer categoria com um objeto inicial i , então qualquer diagrama de forma J tem um limite, ou seja, qualquer objeto isomórfico a F ( i ). Tal isomorfismo determina exclusivamente um cone universal à F .
• Limites topológicos . Limites de funções são um caso especial de limites de filtros , que estão relacionados aos limites categóricos como segue. Dado um espaço topológico X , denote por F o conjunto de filtros em X , x ∈ X um ponto, V ( x ) ∈ F o filtro de vizinhança de x , A ∈ F um filtro particular e o conjunto de filtros mais fino que A e que convergem para x . Os filtros F são dadas uma estrutura categoria pequeno e fino pela adição de uma seta A → B se e apenas se um ⊆ B . A injeção se torna um functor e a seguinte equivalência se mantém:${\ displaystyle F_ {x, A} = \ {G \ in F \ mid V (x) \ cup A \ subset G \}}$${\ displaystyle I_ {x, A}: F_ {x, A} \ a F}$

x é um limite topológico de A se e somente se A é um limite categórico de${\ displaystyle I_ {x, A}}$

Colimits

Exemplos de colimites são fornecidos pelas versões duplas dos exemplos acima:

• Os objetos iniciais são colimites de diagramas vazios.
• Os coprodutos são colimites de diagramas indexados por categorias discretas.
  • Copowers são colimites de diagramas constantes de categorias discretas.
• Coequalizadores são colimites de um par paralelo de morfismos.
  • Cokernels são coequalizadores de um morfismo e um morfismo zero paralelo.
• Pushouts são colimites de um par de morfismos com domínio comum.
• Limites diretos são colimites de diagramas indexados por conjuntos direcionados.

Propriedades

Existência de limites

Um dado diagrama F  : J → C pode ou não ter um limite (ou colimit) em C . Na verdade, pode nem haver um cone para F , muito menos um cone universal.

Uma categoria C é dito que tem limites de forma J se cada diagrama de forma de J possui um limite em C . Especificamente, uma categoria C é dito

• tem produtos se tiver limites de forma J para cada pequena categoria discreta J (não precisa ter produtos grandes),
• tem equalizadores se tiver limites de forma (ou seja, cada par paralelo de morfismos tem um equalizador),${\ displaystyle \ bullet \ rightrightarrows \ bullet}$
• tem retrocessos se tiver limites de forma (ou seja, cada par de morfismos com codomínio comum tem um retrocesso).${\ displaystyle \ bullet \ rightarrow \ bullet \ leftarrow \ bullet}$

Uma categoria completa é uma categoria que possui todos os pequenos limites (ou seja, todos os limites da forma J para cada pequena categoria J ).

Também se pode fazer as definições duais. Uma categoria tem colimites de forma J se cada diagrama de forma de J possui um colimit em C . Uma categoria cocompleta é aquela que contém todos os pequenos colimites.

O teorema de existência para os limites de estados que se uma categoria C tem equalizadores e todos os produtos indexados pelas classes Ob ( J ) e Hom ( J ), então C tem todos os limites da forma J . Neste caso, o limite de um diagrama F  : J → C pode ser construído como o equalizador dos dois morfismos

${\ displaystyle s, t: \ prod _ {i \ in \ operatorname {Ob} (J)} F (i) \ rightrightarrows \ prod _ {f \ in \ operatorname {Hom} (J)} F (\ operatorname { cod} (f))}$

dado (na forma de componente) por

${\ displaystyle {\ begin {alinhados} s & = {\ bigl (} F (f) \ circ \ pi _ {\ operatorname {dom} (f)} {\ bigr)} _ {f \ in \ operatorname {Hom} (J)} \\ t & = {\ bigl (} \ pi _ {\ operatorname {cod} (f)} {\ bigr)} _ {f \ in \ operatorname {Hom} (J)}. \ End {alinhado }}}$

Existe um teorema de existência dual para colimites em termos de coequalizadores e coprodutos. Ambos os teoremas dar condições necessárias e suficientes para a existência de todos os (co) limites de forma J .

Propriedade universal

Limites e colimites são casos especiais importantes de construções universais .

Seja C uma categoria e seja J uma pequena categoria de índice. A categoria functor C ^J pode ser considerada como a categoria de todos os diagramas de forma de J em C . O functor diagonal

${\ displaystyle \ Delta: {\ mathcal {C}} \ to {\ mathcal {C}} ^ {\ mathcal {J}}}$

é o functor que mapeia cada objecto N em C para a constante functor Δ ( N ): J → C para N . Isto é, Δ ( N ) ( X ) = N para cada objecto X em J e Δ ( N ) ( f ) = ID _N para cada morfismo f em J .

Dado um diagrama F : J → C (pensado como um objeto em C ^J ), uma transformação natural ψ  : Δ ( N ) → F (que é apenas um morfismo na categoria C ^J ) é a mesma coisa que um cone de N de F . Para ver esta, primeira nota que Δ ( N ) ( X ) = N para todos os X implica que os componentes de ψ são morphisms vF _X  : N → F ( X ), que toda a parte do domínio N . Além disso, o requisito de que os diagramas do cone comutem é verdadeiro simplesmente porque essa ψ é uma transformação natural. (Dualmente, uma transformação natural ψ  : F → Δ ( N ) é a mesma coisa que um co-cone de F para N. )

Portanto, as definições de limites e colimitos podem ser reafirmadas na forma:

• Um limite de F é um morphism universal de Δ a F .
• Um colimite de F é um morfismo universal de F a Δ.

Adjunções

Como todas as construções universais, a formação de limites e colimites é de natureza funcional. Em outras palavras, se cada diagrama de forma J tem um limite em C (para J pequeno) existe um functor de limite

${\ displaystyle \ lim: {\ mathcal {C}} ^ {\ mathcal {J}} \ to {\ mathcal {C}}}$

que atribui a cada diagrama seu limite e a cada transformação natural η: F → G o morfismo único lim η: lim F → lim G comutando com os cones universais correspondentes. Este é functor adjunto direito à diagonal Δ functor: C → C ^J . Esta adjunção dá uma bijeção entre o conjunto de todos os morfismos de N a lim F e o conjunto de todos os cones de N a F

${\ displaystyle \ operatorname {Hom} (N, \ lim F) \ cong \ operatorname {Cone} (N, F)}$

que é natural nas variáveis N e F . O counit deste adjunção é simplesmente o cone universal de lim F para F . Se a categoria de índice J estiver conectada (e não vazia), então a unidade da adjunção é um isomorfismo, de modo que lim é um inverso à esquerda de Δ. Isso falha se J não estiver conectado. Por exemplo, se J é uma categoria distinta, os componentes da unidade são os morphisms diagonais ô: N → N ^J .

Dualmente, se cada diagrama de forma J tem um colimito em C (para J pequeno) existe um functor colimito

${\ displaystyle \ operatorname {colim}: {\ mathcal {C}} ^ {\ mathcal {J}} \ to {\ mathcal {C}}}$

que atribui a cada diagrama seu colimite. Este functor é deixado adjunto ao functor diagonal Δ: C → C ^J , e um tem um isomorfismo natural

${\ displaystyle \ operatorname {Hom} (\ operatorname {colim} F, N) \ cong \ operatorname {Cocone} (F, N).}$

A unidade deste adjunção é o COCONE universal de F para Colim F . Se J estiver conectado (e não vazio), então a contagem é um isomorfismo, de modo que colim é o inverso à esquerda de Δ.

Observe que ambos os functores limite e colimit são functores covariantes .

Como representações de functores

Pode-se usar functores Hom para relacionar limites e colimitos em uma categoria C aos limites em Set , a categoria dos conjuntos . Isto resulta, em parte, do facto do covariante Hom functor Hom ( N , -): C → Conjunto preserva todos os limites em C . Por dualidade, o functor Hom contravariante deve levar os colimites aos limites.

Se um diagrama F  : J → C tem um limite em C , denotado por lim F , há um isomorfismo canônico

${\ displaystyle \ operatorname {Hom} (N, \ lim F) \ cong \ lim \ operatorname {Hom} (N, F-)}$

que é natural na variável N . Aqui o functor Hom ( N , F -) é a composição do Hom functor Hom ( N , -) com F . Este isomorfismo é o único que respeita os cones limitadores.

Pode-se usar a relação acima para definir o limite de F em C . O primeiro passo é observar que o limite do functor Hom ( N , F -) pode ser identificado com o conjunto de todos os cones de N a F :

${\ displaystyle \ lim \ operatorname {Hom} (N, F -) = \ operatorname {Cone} (N, F).}$

O cone limitante é dada pela família de mapas ¸ _X  : Cone ( N , F ) → Hom ( N , FX ) onde π _X ( ψ ) = ψ _X . Se for dado um objeto L de C junto com um isomorfismo natural Φ  : Hom (-, L ) → Cone (-, F ), o objeto L será um limite de F com o cone limitante dado por Φ _L (id _L ) Em linguagem extravagante, isso equivale a dizer que um limite de F é uma representação do functor Cone (-, F ): C → Set .

Dualmente, se um diagrama F  : J → C tem um colimite em C , denotado colim F , há um isomorfismo canônico único

${\ displaystyle \ operatorname {Hom} (\ operatorname {colim} F, N) \ cong \ lim \ operatorname {Hom} (F-, N)}$

o que é natural na variável N e respeita os cones de colimitação. Identificando o limite de Hom ( F -, N ) com o conjunto Cocone ( F , N ), esta relação pode ser usada para definir o colimite do diagrama F como uma representação do functor Cocone ( F , -).

Intercâmbio de limites e colimitos de conjuntos

Seja I uma categoria finita e J uma pequena categoria filtrada . Para qualquer bifunctor

${\ displaystyle F: I \ times J \ to \ mathbf {Set},}$

existe um isomorfismo natural

${\ displaystyle \ operatorname {colim} \ limits _ {J} \ lim _ {I} F (i, j) \ rightarrow \ lim _ {I} \ operatorname {colim} \ limits _ {J} F (i, j ).}$

Em palavras, colimites filtrados em Set comutam com limites finitos. Ele também afirma que pequenos limites comutam com pequenos limites.

Funções e limites

Se F  : J → C é um diagrama em C e G  : C → D é um functor seguida pela composição (lembrar que um diagrama é apenas um functor) obtém-se um diagrama de GF  : J → D . Uma pergunta natural é então:

“Como os limites de GF se relacionam com os de F ?”

Preservação de limites

Um functor G  : C → D induz um mapa de Cone ( F ) para Cone ( GF ): se Ψ é um cone de N para F então GΨ é um cone de GN para GF . O functor L é dito para preservar os limites de F se ( GL , Gφ ) é um limite de GF sempre que ( G , φ ) é um limite de M . (Observe que se o limite de F não existe, então G preserva vagamente os limites de F. )

Um functor L é dito para preservar todos os limites da forma J se preserva os limites de todos os diagramas F  : J → C . Por exemplo, pode-se dizer que G preserva produtos, equalizadores, retrocessos, etc. Um functor contínuo é aquele que preserva todos os pequenos limites.

Pode-se fazer definições análogas para colimites. Por exemplo, um functor L preserva as colimites de F se G ( G , φ ) é um colimit de GF sempre que ( G , φ ) é um colimit de F . Um functor cocontínuo é aquele que preserva todos os pequenos colimites.

Se C é uma categoria completa , então, pelo teorema de existência acima para limites, um functor G  : C → D é contínuo se e somente se ele preserva (pequenos) produtos e equalizadores. Duplamente, G é co-contínuo se e somente se preserva (pequenos) coprodutos e coequalizadores.

Uma propriedade importante dos functores adjunto é que todo functor adjunto direito é contínuo e todo functor adjunto esquerdo é co-contínuo. Visto que os functores adjuntos existem em abundância, isso dá numerosos exemplos de functores contínuos e co-contínuos.

Para um dado diagrama F  : J → C e functor G  : C → D , se F e GF têm limites especificados, há um morfismo canônico único

${\ displaystyle \ tau _ {F}: G \ lim F \ to \ lim GF}$

que respeita os cones de limite correspondentes. O functor G preserva os limites de F se e somente este mapa for um isomorfismo. Se as categorias C e D têm todos os limites da forma J, então lim é um functor e os morfismos τ _F formam os componentes de uma transformação natural

${\ displaystyle \ tau: G \ lim \ to \ lim G ^ {J}.}$

O functor G preserva todos os limites da forma J se e somente se τ for um isomorfismo natural. Nesse sentido, pode-se dizer que o functor G comuta com limites ( até um isomorfismo natural canônico).

A preservação de limites e colimitos é um conceito que se aplica apenas a functores covariantes . Para functores contravariantes, as noções correspondentes seriam um functor que leva os colimitos aos limites, ou aquele que leva os limites aos colimitos.

Elevação de limites

Diz-se que um functor G  : C → D eleva os limites de um diagrama F  : J → C se sempre que ( L , φ ) é um limite de GF existe um limite ( L ′, φ ′) de F tal que G ( L ′, Φ ′) = ( L , φ ). Um functor L levanta limites da forma J se levanta limites para todos os diagramas de forma de J . Portanto, pode-se falar sobre levantamento de produtos, equalizadores, retrocessos, etc. Finalmente, pode-se dizer que G levanta limites se eleva todos os limites. Existem definições duplas para o levantamento de colimites.

Um functor G eleva os limites exclusivamente para um diagrama F se houver um único cone de pré-imagem ( L ′, φ ′) tal que ( L ′, φ ′) é um limite de F e G ( L ′, φ ′) = ( L , φ ). Pode-se mostrar que G eleva limita exclusivamente se e somente se eleva limites e é amnéstico .

A elevação dos limites está claramente relacionada à preservação dos limites. Se L levanta limites de um diagrama de F e GF tem um limite, então F também tem um limite e L preserva os limites de F . Segue que:

• Se G eleva os limites de todas as formas J e D tem todos os limites da forma J , então C também tem todos os limites da forma J e G preserva esses limites.
• Se G elevar todos os limites pequenos e D for completo, então C também é completo e G é contínuo.

As declarações duais para colimites são igualmente válidas.

Criação e reflexão de limites

Seja F  : J → C um diagrama. Diz-se que um functor G  : C → D

• crie limites para F se sempre que ( L , φ ) for um limite de GF existe um cone único ( L ′, φ ′) para F tal que G ( L ′, φ ′) = ( L , φ ), e além disso, este cone é um limite de M .
• refletir limites para F se cada cone para F cuja imagem em G é um limite de GF é já um limite de F .

Duplamente, pode-se definir criação e reflexão de colimites.

As seguintes declarações são facilmente consideradas equivalentes:

• O functor G cria limites.
• O functor G eleva os limites de maneira única e reflete os limites.

Existem exemplos de functores que elevam os limites de maneira única, mas não os criam nem os refletem.

Exemplos

• Todo functor representável C → Set preserva limites (mas não necessariamente colimites). Em particular, para qualquer objeto A de C , isso é verdade para o functor Hom covariante Hom ( A , -): C → Conjunto .
• O functor esquecido U  : Grp → Set cria (e preserva) todos os pequenos limites e colimites filtrados ; entretanto, U não preserva coprodutos. Esta situação é típica de functores esquecidos algébricos.
• O functor livre F  : Set → Grp (que atribui a cada conjunto S o grupo livre sobre S ) é deixado adjacente ao functor esquecido U e é, portanto, co-contínuo. Isto explica por que o produto livre de dois grupos livres G e H é o grupo livre gerado pela união separado dos geradores de G e H .
• O functor de inclusão Ab → Grp cria limites, mas não preserva coprodutos (o coproduto de dois grupos abelianos sendo a soma direta ).
• O functor esquecido Top → Set eleva limites e colimites exclusivamente, mas não cria nenhum.
• Seja Met _c a categoria de espaços métricos com funções contínuas para morfismos. O functor esquecido Met _c → Set eleva limites finitos, mas não os eleva exclusivamente.

Uma nota sobre a terminologia

A terminologia mais antiga referia-se aos limites como "limites inversos" ou "limites projetivos" e aos colimitos como "limites diretos" ou "limites indutivos". Isso tem sido fonte de muita confusão.

Existem várias maneiras de lembrar a terminologia moderna. Em primeiro lugar,

• cokernels,
• coprodutos,
• coequalizadores, e
• codomínios

são tipos de colimites, enquanto

• grãos,
• produtos
• equalizadores e
• domínios

são tipos de limites. Em segundo lugar, o prefixo "co" implica "primeira variável de ". Termos como "cohomologia" e "co-vibração" têm uma associação ligeiramente mais forte com a primeira variável, ou seja, a variável contravariante do bifunctor. ${\ displaystyle \ operatorname {Hom}}$${\ displaystyle \ operatorname {Hom}}$

Veja também

• Categoria cartesiana fechada  - Tipo de categoria na teoria da categoria
• Equalizador (matemática)  - Conjunto de argumentos em que duas ou mais funções têm o mesmo valor
• Limite inverso  - Construção na teoria da categoria
• Produto (teoria das categorias)  - Objeto generalizado na teoria das categorias

Referências

• Adámek, Jiří; Horst Herrlich; George E. Strecker (1990). Categorias abstratas e concretas (PDF) . John Wiley & Sons. ISBN 0-471-60922-6.
• Mac Lane, Saunders (1998). Categorias para o Matemático Operário . Textos de Pós-Graduação em Matemática . 5 (2ª ed.). Springer-Verlag . ISBN 0-387-98403-8. Zbl  0906.18001 .
• Borceux, Francis (1994). "Limites". Manual de álgebra categórica . Enciclopédia da matemática e suas aplicações 50-51, 53 [ie 52]. Volume 1. Cambridge University Press. ISBN 0-521-44178-1. |volume=tem texto extra ( ajuda )

links externos

• Página web interativa que gera exemplos de limites e colimitos na categoria de conjuntos finitos. Escrito por Jocelyn Paine .
• Limite no nLab