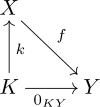Kernel (teoria da categoria) - Kernel (category theory)

Em teoria categoria e suas aplicações para outros ramos da matemática , grãos são uma generalização dos kernels de homomorphisms grupo , os grãos de homomorphisms módulo e certos outros grãos de álgebra . Intuitivamente, o núcleo do morfismo f  : X → Y é o "mais geral" morfismo k  : K → X que produz zero quando composta com (seguido por) f .

Note que os pares de kernel e kernels de diferença (também conhecidos como binários equalizadores ), por vezes, ir pelo nome de "semente"; enquanto relacionadas, estes não são exatamente a mesma coisa e não são discutidos neste artigo.

Definição

Deixe C ser uma categoria . Para definir um kernel no sentido categoria teórico-geral, C precisa ter zero de morphisms . Nesse caso, se f  : X → Y é um arbitrária morfismo em C , em seguida, um núcleo de f é um equalizador de F e o morfismo de zero a partir de X para Y . Em símbolos:

ker ( f ) = eq ( f , 0 _XY )

Para ser mais explícito, a seguinte propriedade universal pode ser usado. Um núcleo de f é um objecto K em conjunto com um morfismo k  : K → X de tal forma que:

• f ∘ k é o morfismo zero a partir de K para Y ;

• Dado qualquer morfismo k ': K ' → X tal que f ∘ k 'é o morfismo de zero, há uma única morfismo u  : K ' → K de tal modo que k ∘ u = K ' .

Note-se que em muitos concretos contextos, seria de se referir ao objeto K como o "núcleo", ao invés do morphism k . Nestas situações, K seria um subconjunto de X , e que seria suficiente para reconstruir k como um mapa de inclusão ; no caso nonconcrete, em contraste, precisamos da morphism k para descrever como K deve ser interpretado como um subobjeto de X . Em qualquer caso, pode-se mostrar que k é sempre uma monomorphism (no sentido categórico da palavra). Pode-se preferir a pensar no kernel como o par ( K ,  k ) em vez de simplesmente K ou k sozinho.

Nem todo morphism precisa ter um kernel, mas se isso acontecer, então todos os seus kernels são isomorfos em um sentido forte: se k  : K → X e ℓ  : L → X são grãos de f  : X → Y , então existe um único isomorfismo φ: K → L de tal modo que l de ∘ φ = k .

Exemplos

Grãos são familiares em muitas categorias de álgebra resumo , tais como a categoria de grupos ou na categoria de (esquerda) módulos ao longo de um determinado anel (incluindo espaços vector mais de um fixo campo ). Para ser explícito, se f  : X → Y é um homomorfismo em uma dessas categorias, e K é o seu núcleo no sentido algébrico de costume , então K é um subálgebra de X eo homomorphism inclusão de K para X é um kernel no sentido categórico.

Note-se que na categoria de monoids , existem kernels categoria teórica assim como para grupos, mas estes kernels não possuem informações suficientes para fins algébricas. Portanto, a noção de núcleo estudado em teoria monoid é um pouco diferente (ver #Relationship algébricas kernels abaixo).

Na categoria de anéis , não há grãos no sentido categoria da teoria; Na verdade, esta categoria não tem sequer de zero morphisms. No entanto, ainda existe uma noção de núcleo estudado em teoria anel que corresponde ao miolo na categoria de pseudo-rings .

Na categoria de espaços topológicos pontiagudos , se f  : X → Y é um mapa pontas contínua, em seguida, o preimage do ponto distinto, K , é um subespaço de X . O mapa inclusão de K em X é o kernel categórica de f .

Relação com outros conceitos categóricas

O conceito dual ao do kernel é a de cokernel . Ou seja, o núcleo de uma morphism é sua cokernel na categoria oposta , e vice-versa.

Como mencionado acima, um núcleo é um tipo de equalizador binário, ou núcleo diferença . Por outro lado, em uma categoria preadditive , cada equalizador binário pode ser construído como um kernel. Para ser mais específico, o equalizador das morphisms de f e g é o núcleo da diferença g - f . Em símbolos:

eq ( f ,  g ) = ker ( g - f ).

É por causa deste fato que equalizadores binários são chamados de "kernels diferença", mesmo em categorias não-preadditive onde morphisms não podem ser subtraídos.

Cada kernel, como qualquer outro equalizador, é um monomorphism . Por outro lado, um monomorphism é chamado de normal, se é o kernel de algum morphism. A categoria é chamada normal, se cada monomorphism é normal.

Categorias abelianas , em particular, estão sempre normal. Nesta situação, o kernel dos cokernel de qualquer morphism (que sempre existe em uma categoria abelian) acaba por ser a imagem de que morphism; em símbolos:

im f = ker coker f (em uma categoria abeliano)

Quando m é um monomorphism, deve ser a sua própria imagem; Assim, não só são categorias abelianas normais, de modo que cada monomorphism é um kernel, mas também sabemos que morphism o monomorphism é um kernel de, a saber, a sua cokernel. Em símbolos:

m = ker (coker m ) (para Monomorfismo numa categoria abeliano)

Relação com kernels algébricas

Álgebra Universal define uma noção de núcleo para homomorphisms entre duas estruturas algébricas da mesma espécie. Este conceito de medidas de kernel quanto o homomorphism dada é de ser injective . Há alguma sobreposição entre esta noção algébrica ea noção categórica do kernel, já que tanto generalizar a situação dos grupos e módulos mencionados acima. Em geral, porém, a noção universal-algébrica de kernel é mais parecido com o conceito de categoria da teoria de par do kernel . Em particular, os pares de kernel pode ser usada para interpretar os kernels em teoria monóide ou teoria anel em termos de categorias de teoria.

Fontes

• Awodey, Steve (2010) [2006]. Categoria Teoria (PDF) . Oxford Guides Logic. 49 (2 ed.). Imprensa da Universidade de Oxford. ISBN  978-0-19-923718-0 .