Sistema radicular - Root system

Grupos de mentiras
Grupos clássicos
Grupos de Lie simples Clássico A n B n C n D n Excepcional G 2 F 4 E 6 E 7 E 8
Outros grupos de Lie Círculo Lorentz Poincaré Grupo Conformal Difeomorfismo Ciclo Euclidiana
Álgebras de Lie
Álgebra de Lie semisimples
Teoria da representação
Grupos de mentiras em física
Cientistas Sophus Lie Henri Poincaré Wilhelm Killing Élie Cartan Hermann Weyl Claude Chevalley Harish-Chandra Armand Borel
Glossário Tabela de grupos de Lie
v t e

Em matemática , um sistema de raízes é uma configuração de vetores em um espaço euclidiano que satisfaz certas propriedades geométricas. O conceito é fundamental na teoria de grupos de Lie e álgebras de Lie , especialmente na classificação e teoria de representação de álgebras de Lie semisimples . Como os grupos de Lie (e alguns análogos, como grupos algébricos ) e álgebras de Lie se tornaram importantes em muitas partes da matemática durante o século XX, a natureza aparentemente especial dos sistemas radiculares desmente o número de áreas em que são aplicados. Além disso, o esquema de classificação para sistemas de raiz, por diagramas Dynkin , ocorre em partes da matemática sem conexão aberta com a teoria de Lie (como a teoria da singularidade ). Finalmente, os sistemas radiculares são importantes por si próprios, como na teoria dos grafos espectrais .

Definições e exemplos

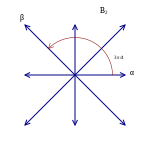
Como um primeiro exemplo, considere os seis vetores no espaço euclidiano bidimensional , R ² , como mostrado na imagem à direita; chame-os de raízes . Esses vetores abrangem todo o espaço. Se você considerar a reta perpendicular a qualquer raiz, digamos β , então o reflexo de R ² nessa reta envia qualquer outra raiz, digamos α , para outra raiz. Além disso, a raiz para a qual é enviado é igual a α + nβ , onde n é um número inteiro (neste caso, n é igual a 1). Esses seis vetores satisfazem a seguinte definição e, portanto, formam um sistema raiz; este é conhecido como A ₂ .

Definição

Seja E um espaço vetorial euclidiano de dimensão finita , com o produto interno euclidiano padrão denotado por . Um sistema de raiz em E é um conjunto finito de vetores diferentes de zero (chamados de raízes ) que satisfazem as seguintes condições: ${\ displaystyle (\ cdot, \ cdot)}$ ${\ displaystyle \ Phi}$

1. As raízes abrangem E .
2. Os únicos múltiplos escalares de uma raiz que pertencem a são ela mesma e .${\ displaystyle \ alpha \ in \ Phi}$${\ displaystyle \ Phi}$${\ displaystyle \ alpha}$${\ displaystyle - \ alpha}$
3. Para cada raiz , o conjunto é fechado sob reflexão através do hiperplano perpendicular a .${\ displaystyle \ alpha \ in \ Phi}$${\ displaystyle \ Phi}$${\ displaystyle \ alpha}$
4. ( Integralidade ) Se e forem raízes em , então a projeção de na linha que atravessa é um inteiro ou múltiplo de meio-inteiro de .${\ displaystyle \ alpha}$${\ displaystyle \ beta}$${\ displaystyle \ Phi}$${\ displaystyle \ beta}$${\ displaystyle \ alpha}$${\ displaystyle \ alpha}$

Uma forma equivalente de escrever as condições 3 e 4 é a seguinte:

3. Para quaisquer duas raízes , o conjunto contém o elemento${\ displaystyle \ alpha, \ beta \ in \ Phi}$${\ displaystyle \ Phi}$${\ displaystyle \ sigma _ {\ alpha} (\ beta): = \ beta -2 {\ frac {(\ alpha, \ beta)} {(\ alpha, \ alpha)}} \ alpha.}$
4. Para quaisquer duas raízes , o número é um inteiro .${\ displaystyle \ alpha, \ beta \ in \ Phi}$${\ displaystyle \ langle \ beta, \ alpha \ rangle: = 2 {\ frac {(\ alpha, \ beta)} {(\ alpha, \ alpha)}}}$

Alguns autores incluem apenas as condições 1–3 na definição de um sistema radicular. Nesse contexto, um sistema radicular que também satisfaça a condição de integralidade é conhecido como sistema radicular cristalográfico . Outros autores omitem a condição 2; então eles chamam de sistemas de raiz que satisfazem a condição 2 reduzida . Neste artigo, todos os sistemas radiculares são considerados reduzidos e cristalográficos.

Em vista da propriedade 3, a condição de integralidade é equivalente a afirmar que β e sua reflexão σ _α ( β ) diferem por um múltiplo inteiro de  α . Observe que o operador

definido pela propriedade 4 não é um produto interno. Não é necessariamente simétrico e é linear apenas no primeiro argumento.

Sistemas de raiz Rank-2

Sistema radicular ${\ displaystyle A_ {1} \ times A_ {1}}$	Sistema radicular ${\ displaystyle D_ {2}}$
Sistema radicular ${\ displaystyle A_ {2}}$	Sistema radicular ${\ displaystyle G_ {2}}$
Sistema radicular ${\ displaystyle B_ {2}}$	Sistema radicular ${\ displaystyle C_ {2}}$

A classificação de um Φ sistema radicular é a dimensão da E . Dois sistemas de raízes podem ser combinados considerando os espaços euclidianos que eles abrangem como subespaços mutuamente ortogonais de um espaço euclidiano comum. Um sistema radicular que não surge dessa combinação, como os sistemas A ₂ , B ₂ e G ₂ ilustrados à direita, é considerado irredutível .

Dois sistemas de raízes ( E ₁ , Φ ₁ ) e ( E ₂ , Φ ₂ ) são chamados de isomórficos se houver uma transformação linear invertível E ₁  →  E ₂ que envia Φ ₁ a Φ _{2 de} modo que para cada par de raízes, o número é preservado. ${\ displaystyle \ langle x, y \ rangle}$

o a rede raiz de um sistema raiz Φ é osubmóduloZdeEgerado por Φ. É umaestruturaem E.

Grupo Weyl

O grupo de isometrias de  E gerado por reflexões através de hiperplanos associados às raízes de Φ é denominado grupo de Weyl de Φ. Por atuar fielmente no conjunto finito Φ, o grupo de Weyl é sempre finito. Os planos de reflexão são os hiperplanos perpendiculares às raízes, indicados por linhas tracejadas na figura abaixo. O grupo de Weyl é o grupo de simetria de um triângulo equilátero, que possui seis elementos. Nesse caso, o grupo Weyl não é o grupo de simetria completo do sistema radicular (por exemplo, uma rotação de 60 graus é uma simetria do sistema radicular, mas não um elemento do grupo Weyl). ${\ displaystyle A_ {2}}$

Classifique um exemplo

Existe apenas um sistema de raiz de classificação 1, consistindo de dois vetores diferentes de zero . Este sistema raiz é chamado . ${\ displaystyle \ {\ alpha, - \ alpha \}}$${\ displaystyle A_ {1}}$

Classifique dois exemplos

Na classificação 2, existem quatro possibilidades, correspondendo a , onde . A figura à direita mostra essas possibilidades, mas com algumas redundâncias: isomorphic to e isomorphic to . ${\ displaystyle \ sigma _ {\ alpha} (\ beta) = \ beta + n \ alpha}$${\ displaystyle n = 0,1,2,3}$${\ displaystyle A_ {1} \ times A_ {1}}$${\ displaystyle D_ {2}}$${\ displaystyle B_ {2}}$${\ displaystyle C_ {2}}$

Observe que um sistema radicular não é determinado pela rede que ele gera: e ambos geram uma rede quadrada enquanto e geram uma rede hexagonal , apenas dois dos cinco tipos possíveis de redes em duas dimensões . ${\ displaystyle A_ {1} \ times A_ {1}}$${\ displaystyle B_ {2}}$${\ displaystyle A_ {2}}$${\ displaystyle G_ {2}}$

Sempre que Φ é um sistema radicular em E , e S é um subespaço de E gerado por Ψ = Φ ∩  S , em seguida, Ψ é um sistema radicular em  S . Assim, a lista exaustiva de quatro sistemas de raízes de classificação 2 mostra as possibilidades geométricas para quaisquer duas raízes escolhidas de um sistema de raízes de classificação arbitrária. Em particular, duas dessas raízes devem se encontrar em um ângulo de 0, 30, 45, 60, 90, 120, 135, 150 ou 180 graus.

Sistemas radiculares decorrentes de álgebras de Lie semisimples

Se for uma álgebra de Lie semi-simples complexa e uma subálgebra de Cartan , podemos construir um sistema de raízes da seguinte maneira. Dizemos que é uma raiz de relativo a se e existe algum tal que ${\ displaystyle {\ mathfrak {g}}}$${\ displaystyle {\ mathfrak {h}}}$${\ displaystyle \ alpha \ in {\ mathfrak {h}} ^ {*}}$${\ displaystyle {\ mathfrak {g}}}$${\ displaystyle {\ mathfrak {h}}}$${\ displaystyle \ alpha \ neq 0}$${\ displaystyle X \ neq 0 \ in {\ mathfrak {g}}}$

para todos . Pode-se mostrar que existe um produto interno para o qual o conjunto de raízes forma um sistema radicular. O sistema raiz de é uma ferramenta fundamental para analisar a estrutura e classificar suas representações. (Consulte a seção abaixo sobre sistemas raiz e teoria de Lie.) ${\ displaystyle H \ in {\ mathfrak {h}}}$${\ displaystyle {\ mathfrak {g}}}$${\ displaystyle {\ mathfrak {g}}}$

História

O conceito de sistema radicular foi originalmente introduzido por Wilhelm Killing por volta de 1889 (em alemão, Wurzelsystem ). Ele os usou em sua tentativa de classificar todas as álgebras de Lie simples no campo dos números complexos . Matar originalmente cometeu um erro na classificação, listando dois sistemas de raiz de classificação 4 excepcionais, quando na verdade há apenas um, agora conhecido como F ₄ . Mais tarde, Cartan corrigiu esse erro, mostrando que os dois sistemas de raiz de Killing eram isomórficos.

Killing investigou a estrutura de uma álgebra de Lie , considerando o que agora é chamado de subálgebra de Cartan . Em seguida, ele estudou as raízes do polinômio característico , onde . Aqui, uma raiz é considerada como uma função ou mesmo como um elemento do espaço vetorial dual . Este conjunto de raízes forma um sistema radicular interno , conforme definido acima, onde o produto interno é a forma de matar . ${\ displaystyle L}$ ${\ displaystyle {\ mathfrak {h}}}$ ${\ displaystyle \ det (\ operatorname {ad} _ {L} xt)}$${\ displaystyle x \ in {\ mathfrak {h}}}$${\ displaystyle {\ mathfrak {h}}}$${\ displaystyle {\ mathfrak {h}} ^ {*}}$${\ displaystyle {\ mathfrak {h}} ^ {*}}$

Consequências elementares dos axiomas do sistema radicular

O cosseno do ângulo entre duas raízes é restrito a metade da raiz quadrada de um inteiro positivo. Isso ocorre porque e são ambos inteiros, por suposição, e ${\ displaystyle \ langle \ beta, \ alpha \ rangle}$${\ displaystyle \ langle \ alpha, \ beta \ rangle}$

Sendo assim , os únicos valores possíveis para são e , correspondendo a ângulos de 90 °, 60 ° ou 120 °, 45 ° ou 135 °, 30 ° ou 150 ° e 0 ° ou 180 °. A condição 2 diz que nenhum múltiplo escalar de α diferente de 1 e −1 pode ser raízes, então 0 ou 180 °, que corresponderia a 2 α ou −2 α , estão fora. O diagrama à direita mostra que um ângulo de 60 ° ou 120 ° corresponde a raízes de igual comprimento, enquanto um ângulo de 45 ° ou 135 ° corresponde a uma razão de comprimento de e um ângulo de 30 ° ou 150 ° corresponde a uma razão de comprimento de . ${\ displaystyle 2 \ cos (\ theta) \ in [-2,2]}$${\ displaystyle \ cos (\ theta)}$${\ displaystyle 0, \ pm {\ tfrac {1} {2}}, \ pm {\ tfrac {\ sqrt {2}} {2}}, \ pm {\ tfrac {\ sqrt {3}} {2} }}$${\ displaystyle \ pm {\ tfrac {\ sqrt {4}} {2}} = \ pm 1}$${\ displaystyle {\ sqrt {2}}}$${\ displaystyle {\ sqrt {3}}}$

Em resumo, aqui estão as únicas possibilidades para cada par de raízes.

• Ângulo de 90 graus; nesse caso, a relação de comprimento é irrestrita.
• Ângulo de 60 ou 120 graus, com uma proporção de comprimento de 1.
• Ângulo de 45 ou 135 graus, com uma proporção de comprimento de .${\ displaystyle {\ sqrt {2}}}$
• Ângulo de 30 ou 150 graus, com uma proporção de comprimento de .${\ displaystyle {\ sqrt {3}}}$

Raízes positivas e raízes simples

Dado um sistema de raízes , sempre podemos escolher (de várias maneiras) um conjunto de raízes positivas . Este é um subconjunto de tal modo que ${\ displaystyle \ Phi}$${\ displaystyle \ Phi ^ {+}}$${\ displaystyle \ Phi}$

• Para cada raiz, exatamente uma das raízes , está contida em .${\ displaystyle \ alpha \ in \ Phi}$${\ displaystyle \ alpha}$${\ displaystyle - \ alpha}$${\ displaystyle \ Phi ^ {+}}$
• Para quaisquer dois distintos, tal que seja uma raiz ,.${\ displaystyle \ alpha, \ beta \ in \ Phi ^ {+}}$${\ displaystyle \ alpha + \ beta}$${\ displaystyle \ alpha + \ beta \ in \ Phi ^ {+}}$

Se um conjunto de raízes positivas for escolhido, os elementos de são chamados de raízes negativas . Um conjunto de raízes positivas pode ser construído escolhendo um hiperplano que não contenha nenhuma raiz e definindo que todas as raízes estão em um lado fixo . Além disso, todo conjunto de raízes positivas surge dessa maneira. ${\ displaystyle \ Phi ^ {+}}$${\ displaystyle - \ Phi ^ {+}}$${\ displaystyle V}$${\ displaystyle \ Phi ^ {+}}$${\ displaystyle V}$

Um elemento de é chamado de raiz simples se não puder ser escrito como a soma de dois elementos de . (O conjunto de raízes simples também é conhecido como base para .) O conjunto de raízes simples é uma base de com as seguintes propriedades especiais adicionais: ${\ displaystyle \ Phi ^ {+}}$${\ displaystyle \ Phi ^ {+}}$${\ displaystyle \ Phi}$${\ displaystyle \ Delta}$${\ displaystyle E}$

• Cada raiz é uma combinação linear de elementos com coeficientes inteiros .${\ displaystyle \ alpha \ in \ Phi}$${\ displaystyle \ Delta}$
• Para cada um , os coeficientes no ponto anterior são todos não negativos ou todos não positivos.${\ displaystyle \ alpha \ in \ Phi}$

Para cada sistema radicular, há muitas opções diferentes do conjunto de raízes positivas - ou, de maneira equivalente, das raízes simples - mas quaisquer dois conjuntos de raízes positivas diferem pela ação do grupo de Weyl. ${\ displaystyle \ Phi}$

Sistema de raiz dupla, coroots e elementos integrais

O sistema de raiz dupla

Se Φ é um sistema radicular em E , o coroot α ^∨ de uma raiz α é definido por

O conjunto de coroots também forma um sistema radicular Φ ^∨ em E , denominado sistema radicular duplo (ou, às vezes, sistema radicular inverso ). Por definição, α ^{∨ ∨} = α, de modo que Φ é o sistema de raiz dual de Φ ^∨ . A rede em E medido por Φ ^∨ é chamada de rede coroot . Ambos Φ e Φ ^∨ têm o mesmo grupo Weyl W e, para s em W ,

Se Δ é um conjunto de raízes simples para Φ, então Δ ^∨ é um conjunto de raízes simples para Φ ^∨ .

Na classificação descrita abaixo, os sistemas de raiz do tipo e junto com os sistemas de raiz excepcionais são todos autoduais, o que significa que o sistema de raiz dual é isomórfico ao sistema de raiz original. Em contraste, os sistemas de raiz e são duais entre si, mas não são isomórficos (exceto quando ). ${\ displaystyle A_ {n}}$${\ displaystyle D_ {n}}$${\ displaystyle E_ {6}, E_ {7}, E_ {8}, F_ {4}, G_ {2}}$${\ displaystyle B_ {n}}$${\ displaystyle C_ {n}}$${\ displaystyle n = 2}$

Elementos integrais

Um vetor em E é chamado de integral se seu produto interno com cada coroot for um inteiro: ${\ displaystyle \ lambda}$

Como o conjunto de com forma uma base para o sistema radicular dual, para verificar se ele é integral, basta verificar a condição acima para . ${\ displaystyle \ alpha ^ {\ vee}}$${\ displaystyle \ alpha \ in \ Delta}$${\ displaystyle \ lambda}$${\ displaystyle \ alpha \ in \ Delta}$

O conjunto de elementos integrais é denominado rede de pesos associada a um determinado sistema radicular. Este termo vem da teoria de representação de álgebras de Lie semisimples , onde os elementos integrais formam os pesos possíveis de representações de dimensão finita.

A definição de um sistema radicular garante que as próprias raízes sejam elementos integrais. Assim, toda combinação linear inteira de raízes também é integral. Na maioria dos casos, entretanto, haverá elementos integrais que não são combinações inteiras de raízes. Ou seja, em geral a rede de pesos não coincide com a rede de raízes.

Classificação de sistemas de raiz por diagramas Dynkin

Um sistema raiz é irredutível se não pode ser particionado na união de dois subconjuntos apropriados , tal que para todos e . ${\ displaystyle \ Phi = \ Phi _ {1} \ cup \ Phi _ {2}}$${\ displaystyle (\ alpha, \ beta) = 0}$${\ displaystyle \ alpha \ in \ Phi _ {1}}$${\ displaystyle \ beta \ in \ Phi _ {2}}$

Os sistemas de raiz irredutíveis correspondem a certos gráficos , os diagramas Dynkin com o nome de Eugene Dynkin . A classificação desses gráficos é uma questão simples de combinatória e induz uma classificação de sistemas de raízes irredutíveis.

Construindo o diagrama Dynkin

Dado um sistema radicular, selecione um conjunto Δ de raízes simples como na seção anterior. Os vértices do diagrama Dynkin associado correspondem às raízes em Δ. As arestas são desenhadas entre os vértices da seguinte maneira, de acordo com os ângulos. (Observe que o ângulo entre as raízes simples é sempre de pelo menos 90 graus.)

• Sem aresta se os vetores forem ortogonais,
• Uma única aresta não direcionada se fizerem um ângulo de 120 graus,
• Uma borda dupla direcionada se eles fizerem um ângulo de 135 graus, e
• Uma aresta tripla direcionada se fizerem um ângulo de 150 graus.

O termo "aresta direcionada" significa que arestas duplas e triplas são marcadas com uma seta apontando para o vetor mais curto. (Pensar na flecha como um sinal de "maior que" deixa claro para qual direção a flecha deve apontar.)

Observe que pelas propriedades elementares das raízes observadas acima, as regras para a criação do diagrama Dynkin também podem ser descritas a seguir. Sem aresta se as raízes forem ortogonais; para raízes não ortogonais, um bordo único, duplo, triplo ou de acordo com se a relação do comprimento do mais curto mais a é 1, , . No caso do sistema radicular, por exemplo, existem duas raízes simples em um ângulo de 150 graus (com uma proporção de comprimento de ). Assim, o diagrama Dynkin possui dois vértices unidos por uma aresta tripla, com uma seta apontando do vértice associado à raiz mais longa para o outro vértice. (Neste caso, a seta é um pouco redundante, uma vez que o diagrama é equivalente a qualquer direção que a seta vá.) ${\ displaystyle {\ sqrt {2}}}$${\ displaystyle {\ sqrt {3}}}$${\ displaystyle G_ {2}}$${\ displaystyle {\ sqrt {3}}}$

Classificação de sistemas de raiz

Embora um determinado sistema de raiz tenha mais de um conjunto possível de raízes simples, o grupo de Weyl age transitivamente em tais escolhas. Consequentemente, o diagrama Dynkin é independente da escolha de raízes simples; é determinado pelo próprio sistema raiz. Por outro lado, dados dois sistemas de raiz com o mesmo diagrama Dynkin, pode-se combinar raízes, começando com as raízes na base, e mostrar que os sistemas são de fato os mesmos.

Assim, o problema de classificação de sistemas de raiz reduz-se ao problema de classificação de possíveis diagramas Dynkin. Um sistema raiz é irredutível se e somente se seus diagramas Dynkin estiverem conectados. Os possíveis diagramas conectados são os indicados na figura. Os subscritos indicam o número de vértices no diagrama (e, portanto, a classificação do sistema raiz irredutível correspondente).

Se for um sistema de raiz, o diagrama Dynkin para o sistema de raiz dual é obtido a partir do diagrama de Dynkin mantendo todos os mesmos vértices e arestas, mas invertendo as direções de todas as setas. Assim, podemos ver em seus diagramas Dynkin que e são duais entre si. ${\ displaystyle \ Phi}$${\ displaystyle \ Phi ^ {\ vee}}$${\ displaystyle \ Phi}$${\ displaystyle B_ {n}}$${\ displaystyle C_ {n}}$

Câmaras Weyl e o grupo Weyl

Se for um sistema radicular, podemos considerar o hiperplano perpendicular a cada raiz . Lembre-se que denota a reflexão sobre o hiperplano e que o grupo Weyl é o grupo de transformações gerado por todos os 's. O complemento do conjunto de hiperplanos é desconectado e cada componente conectado é chamado de câmara de Weyl . Se fixamos um conjunto particular Δ de raízes simples, podemos definir a câmara de Weyl fundamental associada a Δ como o conjunto de pontos tal que para todos . ${\ displaystyle \ Phi \ subset E}$${\ displaystyle \ alpha}$${\ displaystyle \ sigma _ {\ alpha}}$${\ displaystyle E}$${\ displaystyle \ sigma _ {\ alpha}}$${\ displaystyle v \ in E}$${\ displaystyle (\ alpha, v)> 0}$${\ displaystyle \ alpha \ in \ Delta}$

Como os reflexos preservam , eles também preservam o conjunto de hiperplanos perpendiculares às raízes. Assim, cada elemento do grupo de Weyl permeia as câmaras de Weyl. ${\ displaystyle \ sigma _ {\ alpha}, \, \ alpha \ in \ Phi}$${\ displaystyle \ Phi}$

A figura ilustra o caso do sistema radicular. Os "hiperplanos" (neste caso, unidimensionais) ortogonais às raízes são indicados por linhas tracejadas. Os seis setores de 60 graus são as câmaras de Weyl e a região sombreada é a câmara de Weyl fundamental associada à base indicada. ${\ displaystyle A_ {2}}$

Um teorema geral básico sobre as câmaras de Weyl é este:

Teorema : O grupo Weyl atua livre e transitivamente nas câmaras Weyl. Assim, a ordem do grupo de Weyl é igual ao número de câmaras de Weyl.

No caso, por exemplo, o grupo Weyl tem seis elementos e há seis câmaras Weyl. ${\ displaystyle A_ {2}}$

Um resultado relacionado é este:

Teorema : Consertar uma câmara de Weyl . Então, para todos , a órbita de Weyl de contém exatamente um ponto no fechamento de .${\ displaystyle C}$${\ displaystyle v \ in E}$${\ displaystyle v}$${\ displaystyle {\ bar {C}}}$${\ displaystyle C}$

Sistemas de raiz e teoria de Lie

Os sistemas de raiz irredutíveis classificam uma série de objetos relacionados na teoria de Lie, notavelmente o seguinte:

• álgebras de Lie complexas simples (consulte a discussão acima sobre sistemas radiculares decorrentes de álgebras de Lie semissimples),
• grupos de Lie complexos simplesmente conectados que são centros de módulo simples, e
• Grupos de Lie compactos simplesmente conectados que são centros de módulo simples.

Em cada caso, as raízes são pesos diferentes de zero da representação adjunta .

Damos agora uma breve indicação de como os sistemas de raiz irredutíveis classificam as álgebras de Lie simples , seguindo os argumentos de Humphreys. Um resultado preliminar diz que uma álgebra de Lie semisimples é simples se e somente se o sistema radicular associado for irredutível. Assim, restringimos a atenção a sistemas de raízes irredutíveis e álgebras de Lie simples. ${\ displaystyle \ mathbb {C}}$

• Primeiro, devemos estabelecer que para cada álgebra simples existe apenas um sistema radicular. Esta afirmação segue do resultado que a subálgebra de Cartan é única até o automorfismo, do qual se segue que quaisquer duas subálgebras de Cartan dão sistemas de raízes isomórficas.${\ displaystyle {\ mathfrak {g}}}$${\ displaystyle {\ mathfrak {g}}}$
• A seguir, precisamos mostrar que para cada sistema radicular irredutível pode haver no máximo uma álgebra de Lie, ou seja, que o sistema radicular determina a álgebra de Lie até o isomorfismo.
• Finalmente, devemos mostrar que para cada sistema de raiz irredutível, existe uma álgebra de Lie simples associada. Essa afirmação é óbvia para os sistemas de raízes do tipo A, B, C e D, para os quais as álgebras de Lie associadas são as álgebras clássicas. É então possível analisar as álgebras excepcionais caso a caso. Alternativamente, pode-se desenvolver um procedimento sistemático para construir uma álgebra de Lie a partir de um sistema radicular, usando as relações de Serre .

Para conexões entre os sistemas radiculares excepcionais e seus grupos de Lie e álgebras de Lie, consulte E ₈ , E ₇ , E ₆ , F ₄ e G ₂ .

Propriedades dos sistemas de raiz irredutíveis

${\ displaystyle \ Phi}$	${\ displaystyle | \ Phi |}$	${\ displaystyle | \ Phi ^ {<} |}$	eu	D	${\ displaystyle | W |}$
A n ( n  ≥ 1)	n ( n  + 1)			n  + 1	( n  + 1)!
B n ( n  ≥ 2)	2 n 2	2 n	2	2	2 n n !
C n ( n  ≥ 3)	2 n 2	2 n ( n  - 1)	2 n −1	2	2 n n !
D n ( n  ≥ 4)	2 n ( n  - 1)			4	2 n −1 n !
E 6	72			3	51840
E 7	126			2	2903040
E 8	240			1	696729600
F 4	48	24	4	1	1152
G 2	12	6	3	1	12

Os sistemas raiz irredutíveis são nomeados de acordo com seus diagramas Dynkin conectados correspondentes. Existem quatro famílias infinitas (A _n , B _n , C _n e D _n , chamadas de sistemas de raiz clássicos ) e cinco casos excepcionais (os sistemas de raiz excepcionais ). O subscrito indica a classificação do sistema raiz.

Em um sistema radicular irredutível, pode haver no máximo dois valores para o comprimento ( α ,  α ) ^1/2 , correspondendo a raízes curtas e longas . Se todas as raízes têm o mesmo comprimento, são consideradas longas por definição e o sistema radicular é simplesmente entrelaçado ; isso ocorre nos casos A, D e E. Quaisquer duas raízes do mesmo comprimento estão na mesma órbita do grupo de Weyl. No casos não simplesmente atado B, C, G e F, a estrutura de raiz é gerado pelos curtos raízes e as raízes longas abrangem uma subrede, invariante sob o grupo Weyl, igual a r ² /2 vezes a treliça coroot, onde r é o comprimento de uma raiz longa.

Na tabela adjacente, | Φ ^< | denota o número de raízes curtas, I denota o índice na rede raiz da sub-rede gerada por raízes longas, D denota o determinante da matriz de Cartan e | W | denota a ordem do grupo Weyl .

Construção explícita dos sistemas de raízes irredutíveis

A _n

Raízes simples em A ₃

	e 1	e 2	e 3	e 4
α 1	1	-1	0	0
α 2	0	1	-1	0
α 3	0	0	1	-1

Seja E o subespaço de R ^{n +1} para o qual as coordenadas somam 0, e seja Φ o conjunto de vetores em E de comprimento √ 2 e que são vetores inteiros, ou seja , têm coordenadas inteiras em R ^{n +1} . Tal vetor deve ter tudo, exceto duas coordenadas iguais a 0, uma coordenada igual a 1 e uma igual a −1, portanto, há n ² + n raízes ao todo. Uma escolha de raízes simples expressas na base padrão é: α _i = e _i - e _{i +1} , para 1 ≤ i ≤ n.

A reflexão σ _i através do hiperplano perpendicular a α _i é a mesma que a permutação das coordenadas i -ésima e ( i  + 1 ) -ésimas adjacentes . Essas transposições geram o grupo de permutação completo . Para raízes simples adjacentes, σ _i ( α _{i +1} ) = α _{i +1}  +  α _i =  σ _{i +1} ( α _i ) =  α _i  +  α _{i +1} , ou seja, a reflexão é equivalente a adicionar um múltiplo de 1; mas o reflexo de uma raiz simples perpendicular a uma raiz simples não adjacente a deixa inalterada, diferindo por um múltiplo de 0.

A rede raiz A _n - ou seja, a rede gerada pelas raízes A _n - é mais facilmente descrita como o conjunto de vetores inteiros em R ^{n +1} cujas componentes somam zero.

A rede de raiz A ₂ é o arranjo do vértice da telha triangular .

A rede de raiz A ₃ é conhecida pelos cristalógrafos como a rede cúbica centrada na face (ou cúbica compactada ). É o arranjo do vértice do favo de mel tetraédrico-octaédrico .

O sistema de raiz A ₃ (bem como os outros sistemas de raiz de três posições) pode ser modelado no conjunto de construção Zometool .

Em geral, a rede de raiz A _n é o arranjo de vértices do favo de mel simplético n- dimensional .

B _n

Raízes simples em B ₄

	e 1	e 2	e 3	e 4
α 1	1	-1	0	0
α 2	0	1	-1	0
α 3	0	0	1	-1
α 4	0	0	0	1

Seja E = R ⁿ , e seja Φ consistir em todos os vetores inteiros em E de comprimento 1 ou √ 2 . O número total de raízes é 2 n ² . Uma escolha de raízes simples é: α _i = e _i - e _{i +1} , para 1 ≤ i ≤ n - 1 (a escolha acima de raízes simples para A _{n −1} ), e a raiz mais curta α _n = e _n .

A reflexão σ _n através da hiperplana perpendicular ao curto raiz α _n é claro simplesmente negação do n ° de coordenadas. Para a raiz simples longa α _{n −1} , σ _{n −1} ( α _n ) = α _n + α _{n −1} , mas para a reflexão perpendicular à raiz curta, σ _n ( α _{n −1} ) = α _{n −1} + 2 α _n , uma diferença por um múltiplo de 2 em vez de 1.

A rede da raiz B _n - ou seja, a rede gerada pelas raízes B _n - consiste em todos os vetores inteiros.

B ₁ é isomórfico a A ₁ via escala por √ 2 e, portanto, não é um sistema de raiz distinto.

C _n

Raízes simples em C ₄

	e 1	e 2	e 3	e 4
α 1	1	-1	0	0
α 2	0	1	-1	0
α 3	0	0	1	-1
α 4	0	0	0	2

Seja E = R ⁿ , e seja Φ consistir em todos os vetores inteiros em E de comprimento √ 2 junto com todos os vetores da forma 2 λ , onde λ é um vetor inteiro de comprimento 1. O número total de raízes é 2 n ² . Uma escolha de raízes simples é: α _i = e _i - e _{i +1} , para 1 ≤ i ≤ n - 1 (a escolha acima de raízes simples para A _{n −1} ), e a raiz mais longa α _n = 2 e _n . A reflexão σ _n ( α _{n −1} ) = α _{n −1} + α _n , mas σ _{n −1} ( α _n ) = α _n + 2 α _{n −1} .

A rede de raiz C _n - ou seja, a rede gerada pelas raízes C _n - consiste em todos os vetores inteiros cujas componentes somam um inteiro par.

C ₂ é isomórfico a B ₂ por meio de escala em √ 2 e uma rotação de 45 graus e, portanto, não é um sistema radicular distinto.

D _n

Raízes simples em D ₄

	e 1	e 2	e 3	e 4
α 1	1	-1	0	0
α 2	0	1	-1	0
α 3	0	0	1	-1
α 4	0	0	1	1

Seja E = R ⁿ , e seja Φ consistir em todos os vetores inteiros em E de comprimento √ 2 . O número total de raízes é 2 n ( n - 1). Uma escolha de raízes simples é: α _i = e _i - e _{i +1} , para 1 ≤ i ≤ n - 1 (a escolha acima de raízes simples para A _{n −1} ) mais α _n = e _n + e _{n −1} .

A reflexão através do hiperplano perpendicular a α _n é o mesmo que transpor e negar as n- ésimas e ( n - 1) -ésimas coordenadas adjacentes . Qualquer raiz simples e sua reflexão perpendicular a outra raiz simples diferem por um múltiplo de 0 ou 1 da segunda raiz, não por qualquer múltiplo maior.

A rede raiz D _n - ou seja, a rede gerada pelas raízes D _n - consiste em todos os vetores inteiros cujas componentes somam um inteiro par. Este é o mesmo que a rede de raiz C _n .

As raízes D _n são expressas como os vértices de um n - ortoplexo retificado , diagrama de Coxeter-Dynkin :.... Os 2 n ( n −1) vértices existem no meio das arestas do n- ortoplexo.

D ₃ coincide com A ₃ e, portanto, não é um sistema radicular distinto. Os 12 vetores raiz D ₃ são expressos como os vértices de, uma construção de simetria inferior do cuboctaedro .

D ₄ tem simetria adicional chamada trialidade . Os vetores de raiz 24 D ₄ são expressos como os vértices de, uma construção de simetria inferior das 24 células .

E ₆ , E ₇ , E ₈

72 vértices de 1 22 representam os vetores raiz de E 6 (os nós verdes são duplicados nesta projeção do plano de Coxeter E6)	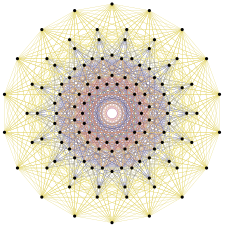126 vértices de 2 31 representam os vetores raiz de E 7	240 vértices de 4 21 representam os vetores raiz de E 8

• O sistema de raiz E ₈ é qualquer conjunto de vetores em R ⁸ que seja congruente com o seguinte conjunto:
  $${\ displaystyle D_ {8} \ cup \ left \ {{\ frac {1} {2}} \ left (\ sum _ {i = 1} ^ {8} \ varejpsilon _ {i} \ mathbf {e} _ {i} \ direita): \ varepsilon _ {i} = \ pm 1, \, \ varepsilon _ {1} \ cdots \ varepsilon _ {8} = + 1 \ right \}.}$$

  

O sistema radicular possui 240 raízes. O conjunto listado é o conjunto de vetores de comprimento √ 2 na rede da raiz E8, também conhecido simplesmente como rede E8 ou Γ ₈ . Este é o conjunto de pontos em R ⁸ , ^de modo que:

1. todas as coordenadas são inteiros ou todas as coordenadas são meio-inteiros (uma mistura de inteiros e meio-inteiros não é permitida), e
2. a soma das oito coordenadas é um número inteiro par .

Assim,

• O sistema radicular E ₇ é o conjunto de vetores em E ₈ que são perpendiculares a uma raiz fixa em E ₈ . O sistema radicular E ₇ possui 126 raízes.
• O sistema radicular E ₆ não é o conjunto de vetores em E ₇ que são perpendiculares a uma raiz fixa em E ₇ , de fato, obtém-se D ₆ dessa forma. No entanto, E ₆ é o subsistema de E ₈ perpendicular a duas raízes adequadamente escolhidas de E ₈ . O sistema radicular E ₆ possui 72 raízes.

Raízes simples em E ₈ : coordenadas pares

1	-1	0	0	0	0	0	0
0	1	-1	0	0	0	0	0
0	0	1	-1	0	0	0	0
0	0	0	1	-1	0	0	0
0	0	0	0	1	-1	0	0
0	0	0	0	0	1	-1	0
0	0	0	0	0	1	1	0
-1/2	-1/2	-1/2	-1/2	-1/2	-1/2	-1/2	-1/2

Uma descrição alternativa da rede E ₈ que às vezes é conveniente é como o conjunto Γ ' ₈ de todos os pontos em R ⁸ tal que

• todas as coordenadas são inteiros e a soma das coordenadas é par, ou
• todas as coordenadas são meio-inteiros e a soma das coordenadas é ímpar.

As redes Γ ₈ e Γ ' ₈ são isomórficas ; um pode passar de um para o outro mudando os sinais de qualquer número ímpar de coordenadas. A rede Γ ₈ é algumas vezes chamada de sistema de coordenadas pares para E _8, enquanto a rede Γ ' ₈ é chamada de sistema de coordenadas ímpares .

Uma escolha de raízes simples para E ₈ no sistema de coordenadas pares com linhas ordenadas por ordem de nó nos diagramas Dynkin alternativos (não canônicos) (acima) é:

α _i = e _i - e _{i +1} , para 1 ≤ i ≤ 6, e

α ₇ = e ₇ + e ₆

(a escolha acima de raízes simples para D ₇ ) junto com

Raízes simples em E ₈ : coordenadas ímpares

1	-1	0	0	0	0	0	0
0	1	-1	0	0	0	0	0
0	0	1	-1	0	0	0	0
0	0	0	1	-1	0	0	0
0	0	0	0	1	-1	0	0
0	0	0	0	0	1	-1	0
0	0	0	0	0	0	1	-1
-1/2	-1/2	-1/2	-1/2	-1/2	1/2	1/2	1/2

Uma escolha de raízes simples para E ₈ no sistema de coordenadas ímpares com linhas ordenadas por ordem de nó em diagramas Dynkin alternativos (não canônicos) (acima) é:

α _i = e _i - e _{i +1} , para 1 ≤ i ≤ 7

(a escolha acima de raízes simples para A ₇ ) junto com

α ₈ = β ₅ , onde

β _j =${\ textstyle {\ frac {1} {2}} \ left (- \ sum _ {i = 1} ^ {j} e_ {i} + \ sum _ {i = j + 1} ^ {8} e_ { eu certo).}$

(Usar β ₃ daria um resultado isomórfico. Usar β _1,7 ou β _2,6 daria simplesmente A ₈ ou D _8. Quanto a β ₄ , suas coordenadas somam 0, e o mesmo é verdadeiro para α _{1 .. .7} , então eles abrangem apenas o subespaço 7-dimensional para o qual as coordenadas somam 0; na verdade −2 β ₄ tem coordenadas (1,2,3,4,3,2,1) na base ( α _i ) .)

Uma vez que a perpendicularidade a α ₁ significa que as duas primeiras coordenadas são iguais, E ₇ é então o subconjunto de E ₈ onde as primeiras duas coordenadas são iguais e, da mesma forma, E ₆ é o subconjunto de E ₈ onde as três primeiras coordenadas são iguais. Isso facilita as definições explícitas de E ₇ e E ₆ como:

E ₇ = { α ∈ Z ⁷ ∪ ( Z +1/2) ⁷  : Σ α _i ² + α ₁ ² = 2, Σ α _i + α ₁ ∈ 2 Z },

E ₆ = { α ∈ Z ⁶ ∪ ( Z +1/2) ⁶  : Σ α _i ² + 2 α ₁ ² = 2, Σ α _i + 2 α ₁ ∈ 2 Z }

Observe que deletar α ₁ e então α ₂ dá conjuntos de raízes simples para E ₇ e E ₆ . No entanto, esses conjuntos de raízes simples estão em subespaços E ₇ e E ₆ de E ₈ diferentes dos escritos acima, uma vez que não são ortogonais a α ₁ ou α ₂ .

F ₄

Raízes simples em F ₄

	e 1	e 2	e 3	e 4
α 1	1	-1	0	0
α 2	0	1	-1	0
α 3	0	0	1	0
α 4	-1/2	-1/2	-1/2	-1/2

Para F ₄ , seja E = R ⁴ , e seja Φ o conjunto de vetores α de comprimento 1 ou √ 2 de modo que as coordenadas de 2α sejam todas inteiras e sejam todas pares ou todas ímpares. Existem 48 raízes neste sistema. Uma escolha de raízes simples é: a escolha de raízes simples fornecidas acima para B ₃ , mais . ${\ textstyle {\ boldsymbol {\ alpha}} _ {4} = - {\ frac {1} {2}} \ sum _ {i = 1} ^ {4} e_ {i}}$

A rede de raiz F ₄ - ou seja, a rede gerada pelo sistema de raiz F ₄ - é o conjunto de pontos em R ^{4, de} modo que todas as coordenadas são inteiras ou todas as coordenadas são meias inteiras (uma mistura de inteiros e meio - inteiros não são permitidos). Esta rede é isomórfica à rede dos quatérnios de Hurwitz .

G ₂

Raízes simples em G ₂

	e 1	e 2	e 3
α 1	1	-1	0
β	-1	2	-1

O sistema radicular G ₂ possui 12 raízes, que formam os vértices de um hexagrama . Veja a foto acima .

Uma escolha de raízes simples é: ( α ₁ , β = α ₂ - α ₁ ) onde α _i = e _i - e _{i +1} para i = 1, 2 é a escolha acima de raízes simples para A ₂ .

A rede da raiz G ₂ - ou seja, a rede gerada pelas raízes G ₂ - é a mesma que a rede da raiz A ₂ .

O poset raiz

O conjunto de raízes positivas é naturalmente ordenado dizendo que se e somente se é uma combinação linear não negativa de raízes simples. Este poset é classificado por , e tem muitas propriedades combinatórias notáveis, uma delas é que se pode determinar os graus dos invariantes fundamentais do grupo de Weyl correspondente a partir desse poset. O gráfico de Hasse é uma visualização da ordem do poset raiz. ${\ displaystyle \ alpha \ leq \ beta}$${\ displaystyle \ beta - \ alpha}$${\ textstyle \ deg \ left (\ sum _ {\ alpha \ in \ Delta} \ lambda _ {\ alpha} \ alpha \ right) = \ sum _ {\ alpha \ in \ Delta} \ lambda _ {\ alpha} }$

Veja também

• Classificação ADE
• Sistema de raiz afim
• Diagrama de Coxeter-Dynkin
• Grupo Coxeter
• Matriz de Coxeter
• Diagrama Dynkin
• datum raiz
• Álgebra de Lie semisimples
• Pesos na teoria da representação de álgebras de Lie semisimples
• Sistema raiz de uma álgebra de Lie semi-simples
• Grupo Weyl

Notas

Referências

• Adams, JF (1983), Lectures on Lie groups , University of Chicago Press, ISBN 0-226-00530-5
• Bourbaki, Nicolas (2002), Lie groups and Lie algebras, Capítulos 4–6 (traduzido do original francês de 1968 por Andrew Pressley) , Elements of Mathematics, Springer-Verlag, ISBN 3-540-42650-7. A referência clássica para sistemas de raiz.
• Bourbaki, Nicolas (1998). Elementos da História da Matemática . Springer. ISBN 3540647678.
• Coleman, AJ (verão de 1989), "O maior artigo matemático de todos os tempos", The Mathematical Intelligencer , 11 (3): 29–38, doi : 10.1007 / bf03025189
• Hall, Brian C. (2015), grupos de Lie, álgebras de Lie e representações: uma introdução elementar , textos de graduação em matemática, 222 (2ª ed.), Springer, ISBN 978-3319134666
• Humphreys, James (1972). Introdução às álgebras de Lie e teoria das representações . Springer. ISBN 0387900535.
• Humphreys, James (1992). Grupos de reflexão e grupos de Coxeter . Cambridge University Press. ISBN 0521436133.
• Killing, Wilhelm (junho de 1888). "Die Zusammensetzung der stetigen endlichen Transformationsgruppen" . Mathematische Annalen . 31 (2): 252–290. doi : 10.1007 / BF01211904 . S2CID  120501356 . Arquivado do original em 05/03/2016.
  • - (março de 1888). "Parte 2" . Matemática. Ann . 33 (1): 1–48. doi : 10.1007 / BF01444109 .
  • - (março de 1889). "Parte 3" . Matemática. Ann . 34 (1): 57–122. doi : 10.1007 / BF01446792 . Arquivado do original em 21/02/2015.
  • - (junho de 1890). "Parte 4" . Matemática. Ann . 36 (2): 161–189. doi : 10.1007 / BF01207837 .
• Kac, Victor G. (1990). Infinite-Dimensional Lie Algebras (3ª ed.). Cambridge University Press. ISBN 978-0-521-46693-6.
• Springer, TA (1998). Linear Algebraic Groups (2ª ed.). Birkhäuser. ISBN 0817640215.

Leitura adicional

• Dynkin, EB (1947). “A estrutura das álgebras semi-simples” . Uspekhi Mat. Nauk . 2 (em russo). 4 (20): 59–127. MR  0027752 .

links externos