Vibração da corda - String vibration

Uma vibração em uma corda é uma onda . A ressonância faz com que uma corda vibrando produza um som com frequência constante , ou seja, altura constante . Se o comprimento ou a tensão da corda forem ajustados corretamente, o som produzido é um tom musical . Cordas vibratórias são a base dos instrumentos de cordas , como violões , violoncelos e pianos .

Aceno

A velocidade de propagação de uma onda em uma corda ( ) é proporcional à raiz quadrada da força de tensão da corda ( ) e inversamente proporcional à raiz quadrada da densidade linear ( ) da corda: ${\ displaystyle v}$${\ displaystyle T}$${\ displaystyle \ mu}$

${\ displaystyle v = {\ sqrt {T \ over \ mu}}.}$

Essa relação foi descoberta por Vincenzo Galilei no final dos anos 1500.

Derivação

Fonte:

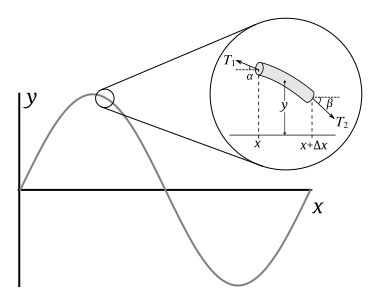
Let Ser o comprimento de um pedaço de corda, sua massa e sua densidade linear . Se os ângulos e forem pequenos, então os componentes horizontais da tensão em ambos os lados podem ser aproximados por uma constante , para a qual a força horizontal líquida é zero. Consequentemente, usando a aproximação de pequeno ângulo, as tensões horizontais agindo em ambos os lados do segmento da corda são dadas por ${\ displaystyle \ Delta x}$${\ displaystyle m}$${\ displaystyle \ mu}$${\ displaystyle \ alpha}$${\ displaystyle \ beta}$${\ displaystyle T}$

${\ displaystyle T_ {1x} = T_ {1} \ cos (\ alpha) \ aprox T.}$

${\ displaystyle T_ {2x} = T_ {2} \ cos (\ beta) \ aprox T.}$

Da segunda lei de Newton para a componente vertical, a massa (que é o produto de sua densidade linear e comprimento) desta peça pela sua aceleração , será igual à força resultante na peça: ${\ displaystyle a}$

${\ displaystyle \ Sigma F_ {y} = T_ {1y} -T_ {2y} = - T_ {2} \ sin (\ beta) + T_ {1} \ sin (\ alpha) = \ Delta ma \ approx \ mu \ Delta x {\ frac {\ partial ^ {2} y} {\ partial t ^ {2}}}.}$

Dividir esta expressão e substituí-la pela primeira e segunda equações obtém-se (podemos escolher a primeira ou a segunda equação para , portanto, escolhemos convenientemente cada uma com o ângulo correspondente e ) ${\ displaystyle T}$${\ displaystyle T}$${\ displaystyle \ beta}$${\ displaystyle \ alpha}$

${\ displaystyle - {\ frac {T_ {2} \ sin (\ beta)} {T_ {2} \ cos (\ beta)}} + {\ frac {T_ {1} \ sin (\ alpha)} {T_ {1} \ cos (\ alpha)}} = - \ tan (\ beta) + \ tan (\ alpha) = {\ frac {\ mu \ Delta x} {T}} {\ frac {\ parcial ^ {2 } y} {\ parcial t ^ {2}}}.}$

De acordo com a aproximação de pequenos ângulos, as tangentes dos ângulos nas pontas do pedaço de corda são iguais às inclinações nas pontas, com um sinal negativo adicional devido à definição de e . Usar esse fato e reorganizar fornece ${\ displaystyle \ alpha}$${\ displaystyle \ beta}$

${\ displaystyle {\ frac {1} {\ Delta x}} \ left (\ left. {\ frac {\ partial y} {\ partial x}} \ right | ^ {x + \ Delta x} - \ left. { \ frac {\ parcial y} {\ parcial x}} \ direita | ^ {x} \ direita) = {\ frac {\ mu} {T}} {\ frac {\ parcial ^ {2} y} {\ parcial t ^ {2}}}.}$

No limite que se aproxima de zero, o lado esquerdo é a definição da segunda derivada de : ${\ displaystyle \ Delta x}$${\ displaystyle y}$

${\ displaystyle {\ frac {\ partial ^ {2} y} {\ partial x ^ {2}}} = {\ frac {\ mu} {T}} {\ frac {\ partial ^ {2} y} { \ parcial t ^ {2}}}.}$

Esta é a equação de onda para , e o coeficiente do segundo termo derivado de tempo é igual a ; portanto ${\ displaystyle y (x, t)}$${\ displaystyle {\ frac {1} {v ^ {2}}}}$

${\ displaystyle v = {\ sqrt {T \ over \ mu}},}$

Onde está a velocidade de propagação da onda na corda (veja o artigo sobre a equação da onda para mais informações). No entanto, esta derivação só é válida para vibrações de pequena amplitude; para aqueles de grande amplitude, não é uma boa aproximação para o comprimento do pedaço de corda, o componente horizontal de tensão não é necessariamente constante. As tensões horizontais não são bem aproximadas por . ${\ displaystyle v}$${\ displaystyle \ Delta x}$${\ displaystyle T}$

Frequência da onda

Uma vez que a velocidade de propagação é conhecida, a frequência do som produzido pela corda pode ser calculada. A velocidade de propagação de uma onda é igual ao comprimento de onda dividido pelo período , ou multiplicado pela frequência :${\ displaystyle \ lambda}$ ${\ displaystyle \ tau}$ ${\ displaystyle f}$

${\ displaystyle v = {\ frac {\ lambda} {\ tau}} = \ lambda f.}$

Se o comprimento da corda for assim , o harmônico fundamental é aquele produzido pela vibração cujos nós são as duas pontas da corda, então o é a metade do comprimento de onda do harmônico fundamental. Portanto, obtém-se as leis de Mersenne : ${\ displaystyle L}$${\ displaystyle L}$

${\ displaystyle f = {\ frac {v} {2L}} = {1 \ over 2L} {\ sqrt {T \ over \ mu}}}$

onde é a tensão (em Newtons), é a densidade linear (ou seja, a massa por unidade de comprimento) e é o comprimento da parte vibrante da corda. Portanto: ${\ displaystyle T}$${\ displaystyle \ mu}$${\ displaystyle L}$

• quanto mais curta for a corda, maior será a frequência da fundamental
• quanto maior a tensão, maior a frequência da fundamental
• quanto mais leve a corda, maior a frequência da fundamental

Além disso, se tomarmos o enésimo harmônico como tendo um comprimento de onda dado por , então facilmente obteremos uma expressão para a frequência do enésimo harmônico: ${\ displaystyle \ lambda _ {n} = 2L / n}$

${\ displaystyle f_ {n} = {\ frac {nv} {2L}}}$

E para uma corda sob tensão T com densidade linear , então ${\ displaystyle \ mu}$

${\ displaystyle f_ {n} = {\ frac {n} {2L}} {\ sqrt {\ frac {T} {\ mu}}}}$

Observando as vibrações das cordas

Pode-se ver as formas de onda em uma corda vibratória se a frequência for baixa o suficiente e a corda vibrante for segurada na frente de uma tela CRT , como uma de uma televisão ou um computador ( não de um osciloscópio analógico). Esse efeito é chamado de efeito estroboscópico , e a taxa na qual a corda parece vibrar é a diferença entre a freqüência da corda e a taxa de atualização da tela. O mesmo pode acontecer com uma lâmpada fluorescente , a uma taxa que é a diferença entre a frequência da corda e a frequência da corrente alternada . (Se a taxa de atualização da tela for igual à frequência da corda ou um múltiplo inteiro dela, a corda parecerá parada, mas deformada.) À luz do dia e outras fontes de luz não oscilantes, este efeito não ocorre e a corda parece parada, mas mais espesso e mais claro ou turvo, devido à persistência da visão .

Um efeito semelhante, mas mais controlável, pode ser obtido usando um estroboscópio . Este dispositivo permite combinar a frequência da lâmpada de flash de xenônio com a frequência de vibração da corda. Em uma sala escura, isso mostra claramente a forma de onda. Caso contrário, pode-se usar a flexão ou, talvez mais facilmente, ajustando os cabeçotes da máquina, para obter o mesmo, ou um múltiplo, da frequência CA para obter o mesmo efeito. Por exemplo, no caso de um violão, a 6ª corda (afinação mais baixa) pressionada até a terceira casa dá um G a 97,999 Hz. Um pequeno ajuste pode alterá-lo para 100 Hz, exatamente uma oitava acima da frequência da corrente alternada na Europa e na maioria dos países da África e Ásia, 50 Hz. Na maioria dos países das Américas - onde a frequência AC é 60 Hz - alterar A # na quinta corda, o primeiro traste de 116,54 Hz a 120 Hz produz um efeito semelhante.

Exemplo do mundo real

A guitarra elétrica Jackson Professional Solist XL de um usuário da Wikipedia tem uma distância de noz- para- ponte (correspondente ao acima) de 25 5 ⁄ 8 pol. E cordas de guitarra elétrica D'Addario XL de níquel super leve EXL-120 com o seguintes especificações do fabricante: ${\ displaystyle L}$

D'Addario EXL-120 especificações do fabricante

String no.	Espessura [pol.] ( )${\ displaystyle d}$	Tensão recomendada [lbs.] ( )${\ displaystyle T}$	${\ displaystyle \ rho}$[g / cm 3 ]
1	0,00899	13,1	7,726 (liga de aço)
2	0,0110	11,0	"
3	0,0160	14,7	"
4	0,0241	15,8	6.533 (liga de aço enrolado em níquel)
5	0,0322	15,8	"
6	0,0416	14,8	"

Dadas as especificações acima, quais seriam as frequências vibracionais computadas ( ) dos harmônicos fundamentais das cordas acima se as cordas fossem esticadas nas tensões recomendadas pelo fabricante? ${\ displaystyle f}$

Para responder a isso, podemos começar com a fórmula da seção anterior, com : ${\ displaystyle n = 1}$

${\ displaystyle f = {\ frac {1} {2L}} {\ sqrt {\ frac {T} {\ mu}}}}$

A densidade linear pode ser expressa em termos da densidade espacial (massa / volume) por meio da relação , onde é o raio da coluna e é o diâmetro (também conhecido como espessura) na tabela acima: ${\ displaystyle \ mu}$${\ displaystyle \ rho}$${\ displaystyle \ mu = \ pi r ^ {2} \ rho = \ pi d ^ {2} \ rho / 4}$${\ displaystyle r}$${\ displaystyle d}$

${\ displaystyle f = {\ frac {1} {2L}} {\ sqrt {\ frac {T} {\ pi d ^ {2} \ rho / 4}}} = {\ frac {1} {2Ld}} {\ sqrt {\ frac {4T} {\ pi \ rho}}} = {\ frac {1} {Ld}} {\ sqrt {\ frac {T} {\ pi \ rho}}}}$

Para efeito de cálculo, podemos substituir a tensão acima, via segunda lei de Newton (Força = massa × aceleração), a expressão , onde é a massa que, na superfície da Terra, teria o peso equivalente correspondente aos valores de tensão em a tabela acima, conforme relacionado através da aceleração padrão devido à gravidade na superfície da Terra, cm / s ² . (Esta substituição é conveniente aqui, uma vez que as tensões das cordas fornecidas pelo fabricante acima são em libras de força , que podem ser mais convenientemente convertidas em massas equivalentes em quilogramas por meio do fator de conversão familiar 1 lb. = 453,59237 g.) A fórmula acima explicitamente torna-se: ${\ displaystyle T}$${\ displaystyle T = ma}$${\ displaystyle m}$${\ displaystyle T}$${\ displaystyle g_ {0} = 980.665}$

${\ displaystyle f _ {\ mathrm {Hz}} = {\ frac {1} {L _ {\ mathrm {in}} \ times 2,54 \ \ mathrm {cm / in} \ times d _ {\ mathrm {in}} \ times 2,54 \ \ mathrm {cm / in}}} {\ sqrt {\ frac {T _ {\ mathrm {lb}} \ times 453,59237 \ \ mathrm {g / lb} \ times 980,665 \ \ mathrm {cm / s ^ {2 }}} {\ pi \ times \ rho _ {\ mathrm {g / cm ^ {3}}}}}}}$

Usando esta fórmula para calcular para a string no. 1 acima rende: ${\ displaystyle f}$

${\ displaystyle f_ {1} = {\ frac {1} {25.625 \ \ mathrm {in} \ times 2,54 \ \ mathrm {cm / in} \ times 0,00899 \ \ mathrm {in} \ times 2,54 \ \ mathrm {cm / in}}} {\ sqrt {\ frac {13.1 \ \ mathrm {lb} \ times 453,59237 \ \ mathrm {g / lb} \ times 980,665 \ \ mathrm {cm / s ^ {2}}} {\ pi \ vezes 7,726 \ \ mathrm {g / cm ^ {3}}}}} \ aprox 330 \ \ mathrm {Hz}}$

Repetir este cálculo para todas as seis cordas resulta nas seguintes frequências. Ao lado de cada frequência, é mostrada a nota musical (em notação científica de afinação ) na afinação padrão da guitarra, cuja frequência é a mais próxima, confirmando que colocar as cordas acima nas tensões recomendadas pelo fabricante realmente resulta nas afinações padrão de uma guitarra:

Harmônicos fundamentais calculados pelas fórmulas de vibração das cordas acima

String no.	Frequência calculada [Hz]	Nota mais próxima na afinação 12-TET do A440
1	330	E 4 (= 440 ÷ 2 5/12 ≈ 329,628 Hz)
2	247	B 3 (= 440 ÷ 2 10/12 ≈ 246,942 Hz)
3	196	G 3 (= 440 ÷ 2 14/12 ≈ 195,998 Hz)
4	147	D 3 (= 440 ÷ 2 19/12 ≈ 146,832 Hz)
5	110	A 2 (= 440 ÷ 2 24/12 = 110 Hz)
6	82,4	E 2 (440 = 2 ÷ 29/12 ≈ 82,407 Hz)

Veja também

• Instrumentos com trastes
• Acústica musical
• Vibrações de um tambor circular
• Experimento de Melde
• 3ª ponte (ressonância harmônica com base em divisões de cordas iguais)
• Ressonância da corda
• Mudança de fase de reflexão

Referências

• Molteno, TCA; NB Tufillaro (setembro de 2004). “Uma investigação experimental sobre a dinâmica de uma corda”. American Journal of Physics . 72 (9): 1157–1169. Bibcode : 2004AmJPh..72.1157M . doi : 10.1119 / 1.1764557 .
• Tufillaro, NB (1989). "Vibrações de cordas não lineares e caóticas". American Journal of Physics . 57 (5): 408. Bibcode : 1989AmJPh..57..408T . doi : 10.1119 / 1.16011 .

Específico

links externos

• " The Vibrating String " de Alain Goriely e Mark Robertson-Tessi, The Wolfram Demonstrations Project .