Teorema de Steinitz - Steinitz's theorem

Na combinatória poliédrica , um ramo da matemática, o teorema de Steinitz é uma caracterização dos grafos não direcionados formados pelas arestas e vértices de poliedros convexos tridimensionais : eles são exatamente os grafos planares conectados por 3 vértices . Ou seja, cada poliedro convexo forma um grafo planar de 3 conexões, e cada grafo planar de 3 conexões pode ser representado como o grafo de um poliedro convexo. Por esse motivo, os gráficos planares de 3 conexões também são conhecidos como gráficos poliédricos .

Este resultado fornece um teorema de classificação para os poliedros convexos tridimensionais, algo que não é conhecido em dimensões superiores. Fornece uma descrição completa e puramente combinatória dos gráficos desses poliedros, permitindo que outros resultados sobre eles, como o teorema de Eberhard sobre a realização de poliedros com determinados tipos de faces, sejam comprovados mais facilmente, sem referência à geometria dessas formas . Além disso, tem sido aplicado no desenho de gráficos , como forma de construir visualizações tridimensionais de gráficos abstratos. Branko Grünbaum chamou esse teorema de "o resultado mais importante e mais profundo conhecido nos 3 politopos ".

O teorema aparece em uma publicação de 1922 de Ernst Steinitz , que deu seu nome. Pode ser provado por indução matemática (como fez Steinitz), encontrando o estado de energia mínima de um sistema de mola bidimensional e elevando o resultado em três dimensões, ou usando o teorema de empacotamento de círculo . Várias extensões do teorema são conhecidas, nas quais o poliedro que realiza um dado gráfico tem restrições adicionais; por exemplo, todo gráfico poliédrico é o gráfico de um poliedro convexo com coordenadas inteiras ou o gráfico de um poliedro convexo cujas arestas são tangentes a uma esfera média comum .

Definições e declaração do teorema

Iluminar o esqueleto de um poliedro convexo de uma fonte de luz próxima a uma de suas faces faz com que suas sombras formem um diagrama de Schlegel planar .

Um gráfico não direcionado é um sistema de vértices e arestas , cada aresta conectando dois dos vértices. A partir de qualquer poliedro, pode-se formar um gráfico, permitindo que os vértices do gráfico correspondam aos vértices do poliedro e conectando quaisquer dois vértices do gráfico por uma aresta sempre que os dois vértices poliedros correspondentes forem os pontos finais de uma aresta do poliedro. Este gráfico é conhecido como o esqueleto do poliedro.

Um gráfico é plano se puder ser desenhado com seus vértices como pontos no plano euclidiano e suas arestas como curvas que conectam esses pontos, de modo que nenhuma curva de aresta se cruze e de modo que o ponto que representa um vértice fique na curva representando uma aresta somente quando o vértice é um ponto final da aresta. Pelo teorema de Fáry , todo desenho plano pode ser endireitado de forma que as curvas que representam as arestas sejam segmentos de linha . Um gráfico é 3-conectado se tiver mais de três vértices e, após a remoção de quaisquer dois de seus vértices, qualquer outro par de vértices permanecerá conectado por um caminho. O teorema de Steinitz afirma que essas duas condições são necessárias e suficientes para caracterizar os esqueletos de poliedros convexos tridimensionais: um dado gráfico é o gráfico de um poliedro tridimensional convexo, se e somente se for plano e conectado por 3 vértices. ${\ displaystyle G}$${\ displaystyle G}$

Provas

Ilustração da prova do teorema de Balinski , mostrando o conjunto zero de uma função linear (azul) passando por dois vértices dados (amarelo) e os caminhos do método simplex conectando o gráfico restante (verde)

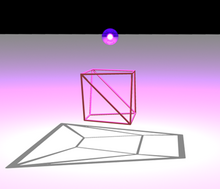
Uma direção do teorema de Steinitz (a direção mais fácil de provar) afirma que o gráfico de cada poliedro convexo é plano e 3-conectado. Conforme mostrado na ilustração, a planaridade pode ser mostrada usando um diagrama de Schlegel : se alguém colocar uma fonte de luz perto de uma face do poliedro e um plano do outro lado, as sombras das bordas do poliedro formarão um gráfico plano, incorporado de forma que as arestas sejam segmentos de linha reta. A conectividade tridimensional de um gráfico poliédrico é um caso especial do teorema de Balinski de que o gráfico de qualquer politopo convexo dimensional está conectado. A conectividade do gráfico de um politopo, após a remoção de qualquer um de seus vértices, pode ser comprovada escolhendo mais um vértice , encontrando uma função linear que é zero no conjunto de vértices resultante , e seguindo os caminhos gerados pelo método simplex para conectar cada vértice para um dos dois vértices extremos da função linear, com o vértice escolhido conectado a ambos. ${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle k-1}$${\ displaystyle v}$${\ displaystyle k}$${\ displaystyle v}$

A outra direção, mais difícil, do teorema de Steinitz afirma que todo grafo planar de 3 conexões é o grafo de um poliedro convexo. Existem três abordagens padrão para esta parte: provas por indução, levantamento de embeddings Tutte bidimensionais em três dimensões usando a correspondência de Maxwell-Cremona e métodos usando o teorema de empacotamento de círculo para gerar um poliedro canônico .

Indução

Transformadas Δ-Y e Y-Δ de um poliedro

Embora a prova original de Steinitz não tenha sido expressa em termos de teoria dos grafos, ela pode ser reescrita nesses termos e envolve encontrar uma sequência de transformações Δ-Y e Y-Δ que reduzem qualquer gráfico planar 3-conectado ao gráfico do tetraedro . Uma transformação Y-Δ remove um vértice de grau três de um gráfico, adicionando arestas entre todos os seus antigos vizinhos se essas arestas ainda não existissem; a transformação reversa, uma transformação Δ-Y, remove as arestas de um triângulo de um gráfico e as substitui por um novo vértice de grau três adjacente aos mesmos três vértices. Uma vez encontrada essa sequência, ela pode ser revertida e convertida em operações geométricas que constroem o poliedro desejado, passo a passo, a partir de um tetraedro. Cada transformação Y-Δ na sequência reversa pode ser realizada geometricamente cortando um vértice de grau três de um poliedro. Uma transformação Δ-Y na sequência reversa pode ser realizada geometricamente removendo uma face triangular de um poliedro e estendendo suas faces vizinhas até o ponto onde elas se encontram, mas somente quando aquele ponto de intersecção triplo das três faces vizinhas está no lado oposto da face removida do poliedro. Quando o ponto de intersecção triplo não está no lado oposto desta face, uma transformação projetiva do poliedro é suficiente para movê-lo para o lado correto. Portanto, por indução no número de transformações Δ-Y e Y-Δ necessárias para reduzir um determinado gráfico a , cada gráfico poliédrico pode ser realizado como um poliedro. ${\ displaystyle K_ {4}}$${\ displaystyle K_ {4}}$

Um trabalho posterior de Epifanov reforçou a prova de Steinitz de que todo gráfico poliédrico pode ser reduzido por transformações Δ-Y e Y-Δ. Epifanov provou que, se dois vértices são especificados em um gráfico planar, o gráfico pode ser reduzido a uma única aresta entre esses terminais combinando as transformadas Δ-Y e Y-Δ com reduções série-paralela . A prova de Epifanov era complicada e não construtiva, mas foi simplificada por Truemper usando métodos baseados em gráficos menores . Truemper observou que todo gráfico de grade é redutível por transformações Δ-Y e Y-Δ dessa maneira, que essa redutibilidade é preservada por menores de gráfico e que todo gráfico planar é menor de um gráfico de grade. Essa ideia pode ser usada para substituir o lema de Steinitz de que existe uma sequência de redução. Após esta substituição, o resto da prova pode ser feito por indução da mesma forma que a prova original de Steinitz. Para essas provas, realizadas usando qualquer uma das formas de encontrar sequências de transformadas Δ-Y e Y-Δ, existem gráficos poliédricos que requerem um número não linear de etapas. Mais precisamente, infinitos gráficos requerem um número de etapas pelo menos proporcional a , onde é o número de vértices no gráfico, e o limite superior mais conhecido no número de etapas suficientes é maior, proporcional a . ${\ displaystyle K_ {4}}$${\ displaystyle n ^ {3/2}}$${\ displaystyle n}$${\ displaystyle n ^ {2}}$

Uma forma alternativa de prova de indução é baseada na remoção de arestas (e compactação dos vértices de grau dois que podem ser deixados após esta remoção) ou arestas de contração e formação de um menor do grafo planar dado. Qualquer gráfico poliédrico pode ser reduzido a um número linear dessas operações e, novamente, as operações podem ser revertidas e as operações invertidas realizadas geometricamente, dando uma realização poliédrica do gráfico. No entanto, embora seja mais simples provar que existe uma sequência de redução para este tipo de argumento, e as sequências de redução são mais curtas, os passos geométricos necessários para inverter a sequência são mais complicados. ${\ displaystyle K_ {4}}$

Elevação

Tensão de equilíbrio no gráfico de um cubo

Um tronco levantando o desenho estressado (com as mesmas posições 2d) em 3d

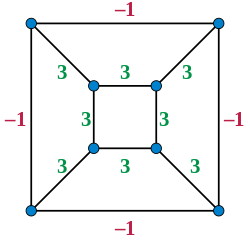
Se um gráfico é desenhado no plano com arestas retas, então uma tensão de equilíbrio é definida como uma atribuição de números reais diferentes de zero (pesos) às arestas, com a propriedade de que cada vértice está na posição dada pela média ponderada de seus vizinhos. De acordo com a correspondência de Maxwell-Cremona, uma tensão de equilíbrio pode ser elevada a uma superfície tridimensional contínua linear por partes, de modo que as arestas que formam os limites entre as partes planas da superfície se projetem para o desenho dado. O peso e o comprimento de cada aresta determinam a diferença nas inclinações da superfície em cada lado da aresta, e a condição de que cada vértice está em equilíbrio com seus vizinhos é equivalente à condição de que essas diferenças de inclinação fazem com que a superfície se encontre -se corretamente na vizinhança do vértice. Pesos positivos se traduzem em ângulos diédricos convexos entre duas faces da superfície linear por partes e os pesos negativos se convertem em ângulos diédricos côncavos. Por outro lado, toda superfície contínua linear por partes vem de uma tensão de equilíbrio dessa maneira. Se um gráfico planar finito for desenhado e dado uma tensão de equilíbrio de tal forma que todas as arestas internas do desenho tenham pesos positivos e todas as arestas externas tenham pesos negativos, então, ao traduzir essa tensão em uma superfície tridimensional desta forma, e então substituindo a superfície plana que representa o exterior do gráfico por seu complemento no mesmo plano, obtém-se um poliedro convexo, com a propriedade adicional de que sua projeção perpendicular ao plano não possui cruzamentos.

A correspondência de Maxwell-Cremona foi usada para obter realizações poliédricas de gráficos poliédricos, combinando-a com um método de desenho de gráfico planar de WT Tutte , a incorporação de Tutte . O método de Tutte começa fixando uma face de um gráfico poliédrico em uma posição convexa no plano. Essa face se tornará a face externa de um desenho de um gráfico. O método continua estabelecendo um sistema de equações lineares nas coordenadas dos vértices, segundo o qual cada vértice restante deve ser colocado na média de seus vizinhos. Então, como Tutte mostrou, esse sistema de equações terá uma solução única em que cada face do gráfico é desenhada como um polígono convexo. Intuitivamente, essa solução descreve o padrão que seria obtido substituindo as arestas internas do gráfico por molas ideais e deixando-as se acomodarem em seu estado de energia mínima. O resultado é quase uma tensão de equilíbrio: se atribuirmos peso um a cada aresta interna, cada vértice interno do desenho estará em equilíbrio. No entanto, nem sempre é possível atribuir números negativos às arestas externas para que também estejam em equilíbrio. Essa atribuição é sempre possível quando a face externa é um triângulo e, portanto, esse método pode ser usado para realizar qualquer gráfico poliédrico que tenha uma face triangular. Se um gráfico poliédrico não contém uma face triangular, seu gráfico dual contém um triângulo e também é poliédrico, então pode-se perceber o dual dessa forma e, então, perceber o gráfico original como o poliedro polar da realização dual. Um método alternativo para realizar poliedros usando elevações evita a dualidade, escolhendo qualquer face com no máximo cinco vértices como face externa. Todo gráfico poliédrico tem tal face e, ao escolher a forma fixa dessa face com mais cuidado, a incorporação de Tutte do resto do gráfico pode ser levantada.

Embalagem de círculo

Um poliedro realizado a partir de um círculo compactado na esfera intermediária azul. Cada vértice de poliedro é representado no empacotamento por seu círculo de horizonte (vermelho). Cada face é representada pelo círculo formado por sua interseção com a esfera.

De acordo com uma variante do teorema de empacotamento de círculo , para cada gráfico poliédrico, existe um sistema de círculos no plano ou em qualquer esfera, representando os vértices e faces do gráfico, de modo que:

• cada dois vértices adjacentes do gráfico são representados por círculos tangentes ,
• cada duas faces adjacentes do gráfico são representadas por um círculo tangente,
• cada par de um vértice e uma face que ele toca são representados por círculos que se cruzam em um ângulo reto , e
• todos os outros pares de círculos são separados uns dos outros.

O mesmo sistema de círculos forma uma representação do gráfico dual , trocando as funções de círculos que representam vértices e círculos que representam faces. A partir de qualquer representação em uma esfera, embutida no espaço euclidiano tridimensional, pode-se formar um poliedro convexo que é combinatorialmente equivalente ao gráfico dado, como uma interseção de meios-espaços cujos limites passam pelos círculos da face. De cada vértice deste poliedro, o horizonte na esfera, visto daquele vértice, é o círculo que o representa. Esta propriedade de horizonte determina a posição tridimensional de cada vértice, e o poliedro pode ser definido de forma equivalente como o casco convexo dos vértices, posicionados desta forma. A esfera se torna a esfera intermediária da realização: cada aresta do poliedro é tangente à esfera, em um ponto onde dois círculos de vértices tangentes cruzam dois círculos de faces tangentes.

Realizações com propriedades adicionais

Coordenadas inteiras

É possível provar uma forma mais forte do teorema de Steinitz, que qualquer gráfico poliédrico pode ser realizado por um poliedro convexo cujas coordenadas são inteiras . Por exemplo, a prova original baseada na indução de Steinitz pode ser fortalecida desta forma. No entanto, os inteiros que resultariam da construção de Steinitz são duplamente exponenciais no número de vértices do gráfico poliédrico dado. Escrever números dessa magnitude em notação binária exigiria um número exponencial de bits. Geometricamente, isso significa que algumas características do poliedro podem ter tamanho duplamente exponencialmente maior do que outras, tornando as realizações derivadas deste método problemáticas para aplicações em desenho gráfico .

Pesquisadores subsequentes descobriram algoritmos de realização baseados em levantamento que usam apenas um número linear de bits por vértice. Também é possível relaxar o requisito de que as coordenadas sejam inteiras e atribuir coordenadas de tal forma que as coordenadas dos vértices sejam inteiros distintos no intervalo de 0 a e as outras duas coordenadas sejam números reais no intervalo de unidade , de modo que cada aresta tenha comprimento de pelo menos um, enquanto o poliedro geral tem volume linear. Alguns gráficos poliédricos são conhecidos por serem realizáveis ​​em grades de tamanho apenas polinomial; em particular, isso é verdadeiro para as pirâmides (realizações de gráficos de roda ), prismas (realizações de gráficos de prisma ) e poliedros empilhados (realizações de redes apolíneas ). ${\ displaystyle x}$${\ displaystyle 2n-4}$

Outra maneira de afirmar a existência de realizações de inteiros é que cada poliedro convexo tridimensional tem um poliedro inteiro combinatorialmente equivalente. Por exemplo, o dodecaedro regular não é ele mesmo um poliedro inteiro, por causa de suas faces pentágonas regulares, mas pode ser realizado como um piritoedro inteiro equivalente . Isso nem sempre é possível em dimensões superiores, onde existem politopos (como os construídos a partir da configuração de Perles ) que não possuem equivalente inteiro.

Inclinações iguais

Um grafo Halin é um caso especial de um grafo poliédrico, formado a partir de uma árvore embutida no plano (sem vértices de grau dois) conectando as folhas da árvore em um ciclo . Para gráficos Halin, pode-se escolher realizações poliédricas de um tipo especial: o ciclo externo forma uma face de base convexa horizontal e todas as outras faces ficam diretamente acima da face de base (como no poliedro realizado por levantamento), com todas essas faces superiores tendo a mesma inclinação. Superfícies poliédricas com faces de inclinação igual sobre qualquer polígono de base (não necessariamente convexo) podem ser construídas a partir do esqueleto reto do polígono , e uma forma equivalente de descrever esta realização é que a projeção bidimensional da árvore sobre a face de base forma sua linha reta esqueleto. A prova desse resultado usa a indução: qualquer árvore enraizada pode ser reduzida a uma árvore menor removendo as folhas de um nó interno cujos filhos são todos folhas, o gráfico de Halin formado a partir da árvore menor tem uma realização pela hipótese de indução, e é possível modificar esta realização para adicionar qualquer número de filhos folha ao nó da árvore cujos filhos foram removidos.

Especificando a forma de um rosto

Em qualquer poliedro que representa um dado gráfico poliédrico , as faces de são exatamente os ciclos em que não se separam em dois componentes: isto é, remover um ciclo facial das folhas do resto de como um subgrafo conectado. Esses ciclos são chamados de ciclos periféricos . Assim, a estrutura combinatória das faces (mas não de suas formas geométricas) é determinada exclusivamente a partir da estrutura do gráfico. Outro reforço do teorema de Steinitz, de Barnette e Grünbaum, afirma que para qualquer gráfico poliédrico, qualquer face do gráfico e qualquer polígono convexo que representa essa face, é possível encontrar uma realização poliédrica de todo o gráfico que tem a forma especificada para o rosto designado. Isso está relacionado a um teorema de Tutte, de que qualquer gráfico poliédrico pode ser desenhado no plano com todas as faces convexas e qualquer forma especificada para sua face externa. No entanto, os desenhos gráficos planos produzidos pelo método de Tutte não necessariamente se elevam para poliedros convexos. Em vez disso, Barnette e Grünbaum provam esse resultado usando um método indutivo. Também é sempre possível, dado um gráfico poliédrico e um ciclo arbitrário em , encontrar uma realização para a qual forma a silhueta da realização sob projeção paralela . ${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle G}$${\ displaystyle C}$${\ displaystyle G}$${\ displaystyle C}$

Esferas tangentes

A realização de poliedros usando o teorema de empacotamento de círculo fornece outro fortalecimento do teorema de Steinitz: cada grafo planar de 3 conexões pode ser representado como um poliedro convexo de tal forma que todas as suas arestas são tangentes à mesma esfera unitária , a esfera média do poliedro. Ao realizar uma transformação Möbius cuidadosamente escolhida de um empacotamento de círculo antes de transformá-lo em um poliedro, é possível encontrar uma realização poliédrica que realiza todas as simetrias do gráfico subjacente, no sentido de que todo automorfismo de gráfico é uma simetria da realização poliédrica . Mais geralmente, se for um gráfico poliédrico e qualquer corpo convexo tridimensional liso , é possível encontrar uma representação poliédrica de em que todas as arestas são tangentes . ${\ displaystyle G}$${\ displaystyle K}$${\ displaystyle G}$${\ displaystyle K}$

Os métodos de empacotamento de círculo também podem ser usados ​​para caracterizar os gráficos de poliedros que têm uma circunsfera em todos os seus vértices ou uma tangente na esfera interna a todas as suas faces. (Os poliedros com uma circunsfera também são significativos na geometria hiperbólica como poliedros ideais .) Em ambos os casos, a existência de uma esfera é equivalente à solubilidade de um sistema de desigualdades lineares em variáveis ​​reais positivas associadas a cada aresta do gráfico. No caso da esfera interna, essas variáveis ​​devem somar exatamente uma em cada ciclo de face do gráfico e mais de uma em cada ciclo sem face. Duplamente, para a circunsfera, as variáveis ​​devem somar uma em cada vértice e mais de uma em cada corte com dois ou mais vértices em cada lado do corte. Embora possa haver exponencialmente muitas desigualdades lineares a serem satisfeitas, uma solução (se houver) pode ser encontrada em tempo polinomial usando o método elipsóide . Os valores das variáveis ​​de uma solução determinam os ângulos entre pares de círculos em um empacotamento de círculos cujo poliedro correspondente tem a relação desejada com sua esfera.

Resultados relacionados

Os gráficos de poliedros tridimensionais não convexos podem não estar conectados (à esquerda), e mesmo para poliedros topologicamente esféricos cujas faces são polígonos simples, esses gráficos podem não ser 3 conectados (à direita).

Em qualquer dimensão superior a três, o problema de Steinitz algorítmico consiste em determinar se uma dada rede é a rede de face de um politopo convexo . É improvável que tenha complexidade de tempo polinomial, pois é NP-difícil e mais fortemente completo para a teoria existencial dos reais , mesmo para politopos quadridimensionais, pelo teorema da universalidade de Richter-Gebert. Aqui, a teoria existencial dos reais é uma classe de problemas computacionais que podem ser formulados em termos de encontrar variáveis ​​reais que satisfaçam um determinado sistema de equações polinomiais e desigualdades. Para o problema de Steinitz algorítmico, as variáveis ​​de tal problema podem ser as coordenadas do vértice de um politopo, e as equações e desigualdades podem ser usadas para especificar o nivelamento de cada face na rede de face dada e a convexidade de cada ângulo entre as faces. Completude significa que todos os outros problemas nesta classe podem ser transformados em uma instância equivalente do problema algorítmico de Steinitz, em tempo polinomial. A existência de tal transformação implica que, se o problema de Steinitz algorítmico tem uma solução de tempo polinomial, então o mesmo acontece com todos os problemas na teoria existencial dos reais e todos os problemas em NP. No entanto, como um dado gráfico pode corresponder a mais de uma rede de faces, é difícil estender esse resultado de completude ao problema de reconhecimento de gráficos de 4 politopos. A determinação da complexidade computacional deste problema de reconhecimento de grafos permanece em aberto.

Os pesquisadores também encontraram caracterizações de grafos teóricos dos gráficos de certas classes especiais de poliedros tridimensionais não convexos e politopos convexos quadridimensionais. No entanto, em ambos os casos, o problema geral permanece sem solução. Na verdade, mesmo o problema de determinar quais gráficos completos são os gráficos de poliedros não convexos (exceto para o tetraedro e para o poliedro Császár ) permanece sem solução. ${\ displaystyle K_ {4}}$${\ displaystyle K_ {7}}$

O teorema de Eberhard caracteriza parcialmente os multiconjuntos de polígonos que podem ser combinados para formar as faces de um poliedro convexo. Isso pode ser provado formando um gráfico planar de 3 conexões com o determinado conjunto de faces poligonais e, em seguida, aplicando o teorema de Steinitz para encontrar uma realização poliédrica desse gráfico.

László Lovász mostrou uma correspondência entre representações poliédricas de grafos e matrizes realizando os invariantes do grafo de Colin de Verdière dos mesmos grafos. O invariante de Colin de Verdière é o corank máximo de uma matriz de adjacência ponderada do grafo, sob algumas condições adicionais que são irrelevantes para grafos poliédricos. São matrizes quadradas simétricas indexadas pelos vértices, com o peso do vértice no coeficiente diagonal e com o peso da aresta nos coeficientes fora da diagonal e . Quando os vértices e não são adjacentes, o coeficiente deve ser zero. Este invariante é no máximo três se e somente se o gráfico for um gráfico plano . Como mostra Lovász, quando o gráfico é poliédrico, uma representação dele como um poliedro pode ser obtida encontrando uma matriz de adjacência ponderada do corank três, encontrando três vetores formando uma base para seu espaço nulo , usando os coeficientes desses vetores como coordenadas para o vértices de um poliedro, e escalar esses vértices apropriadamente. ${\ displaystyle i}$${\ displaystyle M_ {i, i}}$${\ displaystyle i, j}$${\ displaystyle M_ {i, j}}$${\ displaystyle M_ {j, i}}$${\ displaystyle i}$${\ displaystyle j}$${\ displaystyle M_ {i, j}}$

História

A história do teorema de Steinitz é descrita por Grünbaum (2007) , que observa sua primeira aparição de forma enigmática em uma publicação de Ernst Steinitz , originalmente escrita em 1916. Steinitz forneceu mais detalhes em notas de aula posteriores, publicadas após sua morte em 1928. Embora os tratamentos modernos do teorema de Steinitz o afirmem como uma caracterização teórica dos gráficos de poliedros, Steinitz não usava a linguagem dos gráficos. A formulação teórica dos grafos do teorema foi introduzida no início dos anos 1960 por Branko Grünbaum e Theodore Motzkin , com sua prova também convertida em teoria dos grafos no texto Convex Polytopes de Grünbaum de 1967 . O trabalho de Epifanov nas transformadas Δ-Y e Y-Δ, reforçando a prova de Steinitz, foi motivado por outros problemas além da caracterização de poliedros. Truemper (1989) credita a Grünbaum a observação da relevância deste trabalho para o teorema de Steinitz.

A correspondência Maxwell-Cremona entre diagramas de tensões e elevações poliédricas foi desenvolvida em uma série de artigos de James Clerk Maxwell de 1864 a 1870, com base em trabalhos anteriores de Pierre Varignon , William Rankine e outros, e foi popularizada no final do século 19 por Luigi Cremona . A observação de que essa correspondência pode ser usada com a incorporação de Tutte para provar o teorema de Steinitz vem de Eades e Garvan (1995) .

O teorema de empacotamento de círculos foi provado por Paul Koebe em 1936 e (independentemente) por EM Andreev em 1970; foi popularizado em meados da década de 1980 por William Thurston , que (apesar de citar Koebe e Andreev) é frequentemente creditado como um de seus descobridores. A versão de Andreev do teorema já foi formulada como uma caracterização do tipo Steinitz para certos poliedros no espaço hiperbólico , e o uso de empacotamento em círculo para realizar poliedros com esferas médias vem do trabalho de Thurston. O problema de caracterizar poliedros com esferas inscritas ou circunscritas, eventualmente resolvido usando um método baseado em realizações de empacotamento de círculos, remonta ao trabalho não publicado de René Descartes por volta de 1630 e a Jakob Steiner em 1832; os primeiros exemplos de poliedros que não têm realização com uma circunsfera ou insfera foram dados por Steinitz em 1928.

Referências