Coordenadas generalizadas - Generalized coordinates

Em mecânica analítica , o termo coordenadas generalizadas se refere aos parâmetros que descrevem a configuração do sistema em relação a alguma configuração de referência. Esses parâmetros devem definir exclusivamente a configuração do sistema em relação à configuração de referência. Isso é feito assumindo que isso pode ser feito com um único gráfico . As velocidades generalizadas são as derivadas de tempo das coordenadas generalizadas do sistema.

Um exemplo de coordenada generalizada é o ângulo que localiza um ponto que se move em um círculo. O adjetivo "generalizado" distingue esses parâmetros do uso tradicional do termo coordenada para se referir a coordenadas cartesianas : por exemplo, descrever a localização do ponto no círculo usando as coordenadas xey.

Embora possa haver muitas opções de coordenadas generalizadas para um sistema físico, os parâmetros que são convenientes são normalmente selecionados para a especificação da configuração do sistema e que tornam a solução de suas equações de movimento mais fácil. Se esses parâmetros são independentes um do outro, o número de coordenadas generalizadas independentes é definido pelo número de graus de liberdade do sistema.

Coordenadas generalizadas são emparelhadas com momentos generalizados para fornecer coordenadas canônicas no espaço de fase .

Restrições e graus de liberdade

Caminho reto aberto

Caminho curvo aberto F ( x , y ) = 0

Caminho curvo fechado C ( x , y ) = 0

Uma coordenada generalizada (um grau de liberdade) em caminhos em 2D. Apenas uma coordenada generalizada é necessária para especificar exclusivamente as posições na curva. Nestes exemplos, essa variável é o comprimento do arco s ou o ângulo θ . Ter ambas as coordenadas cartesianas ( x , y ) é desnecessário, uma vez que x ou y está relacionado um ao outro pelas equações das curvas. Eles também podem ser parametrizados por s ou θ .

Caminho curvo aberto F ( x , y ) = 0. Intersecções múltiplas de raio com caminho.

Caminho curvo fechado C ( x , y ) = 0. Auto-intersecção do caminho.

O comprimento do arco s ao longo da curva é uma coordenada generalizada legítima, uma vez que a posição é determinada exclusivamente, mas o ângulo θ não é, pois há várias posições para um único valor de θ .

Coordenadas generalizadas são normalmente selecionadas para fornecer o número mínimo de coordenadas independentes que definem a configuração de um sistema, o que simplifica a formulação das equações de movimento de Lagrange . No entanto, também pode ocorrer que um conjunto útil de coordenadas generalizadas possa ser dependente , o que significa que elas estão relacionadas por uma ou mais equações de restrição .

Restrições holonômicas

Superfície curva aberta F ( x , y , z ) = 0

Superfície curva fechada S ( x , y , z ) = 0

Duas coordenadas generalizadas, dois graus de liberdade, em superfícies curvas em 3D. Apenas dois números ( u , v ) são necessários para especificar os pontos na curva, uma possibilidade é mostrada para cada caso. As três coordenadas cartesianas completas ( x , y , z ) não são necessárias porque quaisquer duas determinam a terceira de acordo com as equações das curvas.

Para um sistema de N partículas no espaço de coordenadas reais 3D , o vetor de posição de cada partícula pode ser escrito como uma tripla em coordenadas cartesianas :

{\ displaystyle \ mathbf {r} _ {1} = (x_ {1}, y_ {1}, z_ {1}) \ ,, \ quad \ mathbf {r} _ {2} = (x_ {2}, y_ {2}, z_ {2}) \ ,, \ ldots \ ,, \ mathbf {r} _ {N} = (x_ {N}, y_ {N}, z_ {N}) \ ,.}

Qualquer um dos vetores de posição pode ser denotado como r _k, onde k = 1, 2, ..., N rotula as partículas. Uma restrição holonômica é uma equação de restrição da forma da partícula k

{\ displaystyle f (\ mathbf {r} _ {k}, t) = 0}

que conecta todas as 3 coordenadas espaciais daquela partícula juntas, então elas não são independentes. A restrição pode mudar com o tempo, então o tempo t aparecerá explicitamente nas equações de restrição. Em qualquer instante, qualquer coordenada será determinada a partir das outras coordenadas, por exemplo, se x _k e z _k são dados, então o mesmo ocorre com y _k . Uma equação de restrição conta como uma restrição. Se houver restrições C , cada uma terá uma equação, portanto, haverá equações de restrição C. Não há necessariamente uma equação de restrição para cada partícula e, se não houver restrições no sistema, não haverá equações de restrição.

Até agora, a configuração do sistema é definida por 3 N quantidades, mas as coordenadas C podem ser eliminadas, uma coordenada de cada equação de restrição. O número de coordenadas independentes é n = 3 N - C . (Em dimensões D , a configuração original precisaria de coordenadas ND , e a redução por restrições significa n = ND - C ). É ideal usar o número mínimo de coordenadas necessárias para definir a configuração de todo o sistema, aproveitando as restrições do sistema. Essas quantidades são conhecidas como coordenadas generalizadas neste contexto, denotadas por q _j ( t ). É conveniente agrupá-los em uma n - tupla

{\ displaystyle \ mathbf {q} (t) = (q_ {1} (t), q_ {2} (t), \ ldots, q_ {n} (t))}

que é um ponto no espaço de configuração do sistema. Eles são todos independentes uns dos outros e cada um é uma função do tempo. Geometricamente, eles podem ter comprimentos ao longo de linhas retas ou comprimentos de arco ao longo de curvas ou ângulos; não necessariamente coordenadas cartesianas ou outras coordenadas ortogonais padrão . Há um para cada grau de liberdade , então o número de coordenadas generalizadas é igual ao número de graus de liberdade, n . Um grau de liberdade corresponde a uma quantidade que muda a configuração do sistema, por exemplo, o ângulo de um pêndulo ou o comprimento do arco percorrido por um cordão ao longo de um fio.

Se for possível encontrar a partir das restrições tantas variáveis independentes quantos graus de liberdade, elas podem ser usadas como coordenadas generalizadas. O vetor posição r _k da partícula k é uma função de todas as n coordenadas generalizadas (e, através delas, do tempo),

{\ displaystyle \ mathbf {r} _ {k} = \ mathbf {r} _ {k} (\ mathbf {q} (t)) \ ,,}

e as coordenadas generalizadas podem ser consideradas como parâmetros associados à restrição.

As derivadas de tempo correspondentes de q são as velocidades generalizadas ,

{\ displaystyle {\ dot {\ mathbf {q}}} = {\ frac {d \ mathbf {q}} {dt}} = ({\ dot {q}} _ {1} (t), {\ dot {q}} _ {2} (t), \ ldots, {\ dot {q}} _ {n} (t))}

(cada ponto sobre uma quantidade indica uma derivada de tempo ). O vetor velocidade v _k é a derivada total de r _k em relação ao tempo

{\ displaystyle \ mathbf {v} _ {k} = {\ dot {\ mathbf {r}}} _ {k} = {\ frac {d \ mathbf {r} _ {k}} {dt}} = \ soma _ {j = 1} ^ {n} {\ frac {\ partial \ mathbf {r} _ {k}} {\ partial q_ {j}}} {\ dot {q}} _ {j} \ ,. }

e então geralmente depende das velocidades e coordenadas generalizadas. Como somos livres para especificar os valores iniciais das coordenadas generalizadas e velocidades separadamente, as coordenadas generalizadas q _j e as velocidades dq _j / dt podem ser tratadas como variáveis independentes .

Restrições não holonômicas

Um sistema mecânico pode envolver restrições tanto nas coordenadas generalizadas quanto em seus derivados. Restrições desse tipo são conhecidas como não holonômicas. Restrições não holonômicas de primeira ordem têm a forma

{\ displaystyle g (\ mathbf {q}, {\ dot {\ mathbf {q}}}, t) = 0 \ ,,}

Um exemplo de tal restrição é uma roda giratória ou fio de faca que restringe a direção do vetor de velocidade. Restrições não holonômicas também podem envolver derivadas de próxima ordem, como acelerações generalizadas.

Quantidades físicas em coordenadas generalizadas

Energia cinética

A energia cinética total do sistema é a energia do movimento do sistema, definida como

{\ displaystyle T = {\ frac {1} {2}} \ sum _ {k = 1} ^ {N} m_ {k} {\ dot {\ mathbf {r}}} _ {k} \ cdot {\ ponto {\ mathbf {r}}} _ {k} \ ,,}

em que · é o produto escalar . A energia cinética é função apenas das velocidades v _k , não das próprias coordenadas r _k . Em contraste, uma observação importante é

{\ displaystyle {\ dot {\ mathbf {r}}} _ {k} \ cdot {\ dot {\ mathbf {r}}} _ {k} = \ sum _ {i, j = 1} ^ {n} \ left ({\ frac {\ partial \ mathbf {r} _ {k}} {\ partial q_ {i}}} \ cdot {\ frac {\ partial \ mathbf {r} _ {k}} {\ partial q_ {j}}} \ right) {\ dot {q}} _ {i} {\ dot {q}} _ {j},}

que ilustra que a energia cinética é em geral uma função das velocidades generalizadas, coordenadas e tempo se as restrições também variam com o tempo, então T = T ( q , d q / dt , t ).

No caso de as restrições nas partículas serem independentes do tempo, então todas as derivadas parciais com respeito ao tempo são zero, e a energia cinética é uma função homogênea de grau 2 nas velocidades generalizadas.

Ainda para o caso independente do tempo, esta expressão é equivalente a tomar o elemento de linha ao quadrado da trajetória para a partícula k ,

{\ displaystyle ds_ {k} ^ {2} = d \ mathbf {r} _ {k} \ cdot d \ mathbf {r} _ {k} = \ sum _ {i, j = 1} ^ {n} \ esquerda ({\ frac {\ parcial \ mathbf {r} _ {k}} {\ parcial q_ {i}}} \ cdot {\ frac {\ parcial \ mathbf {r} _ {k}} {\ parcial q_ { j}}} \ right) dq_ {i} dq_ {j} \ ,,}

e dividindo pelo diferencial ao quadrado no tempo, dt ² , para obter o quadrado da velocidade da partícula k . Assim, para restrições independentes do tempo, é suficiente conhecer o elemento da linha para obter rapidamente a energia cinética das partículas e, portanto, a Lagrangiana.

É instrutivo ver os vários casos de coordenadas polares em 2d e 3d, devido ao seu aparecimento frequente. Em 2d coordenadas polares ( r , θ ),

{\ displaystyle \ left ({\ frac {ds} {dt}} \ right) ^ {2} = {\ dot {r}} ^ {2} + r ^ {2} {\ dot {\ theta}} ^ {2} \ ,,}

em coordenadas cilíndricas 3d ( r , θ , z ),

{\ displaystyle \ left ({\ frac {ds} {dt}} \ right) ^ {2} = {\ dot {r}} ^ {2} + r ^ {2} {\ dot {\ theta}} ^ {2} + {\ ponto {z}} ^ {2} \ ,,}

em coordenadas esféricas 3d ( r , θ , φ ),

{\ displaystyle \ left ({\ frac {ds} {dt}} \ right) ^ {2} = {\ dot {r}} ^ {2} + r ^ {2} {\ dot {\ theta}} ^ {2} + r ^ {2} \ sin ^ {2} \ theta \, {\ dot {\ varphi}} ^ {2} \ ,.}

Momento generalizado

O momento generalizado " canonicamente conjugado a" a coordenada q _i é definido por

{\ displaystyle p_ {i} = {\ frac {\ partial L} {\ partial {\ dot {q}} _ {i}}}.}

Se o lagrangiano L que não dependem de algum coordenar q _i , segue-se a partir das equações de Euler-Lagrange que a dinâmica generalizada correspondente será uma quantidade conservada , porque o tempo derivado é zero implicando o impulso é uma constante do movimento;

{\ displaystyle {\ dot {p}} _ {i} = {\ frac {d} {dt}} {\ frac {\ partial L} {\ partial {\ dot {q}} _ {i}}} = {\ frac {\ parcial L} {\ parcial q_ {i}}} = 0 \ ,.}

Exemplos

Conta em um fio

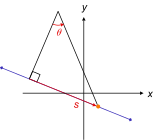
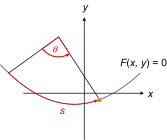
Talão restringido para se mover em um fio sem atrito. O fio exerce uma força de reação C no cordão para mantê-lo no fio. A força não restritiva N , neste caso, é a gravidade. Observe que a posição inicial do fio pode levar a diferentes movimentos.

Para um cordão deslizando em um fio sem fricção sujeito apenas à gravidade no espaço 2d, a restrição no cordão pode ser declarada na forma f ( r ) = 0, onde a posição do cordão pode ser escrita r = ( x ( s ) , y ( s )), em que s é um parâmetro, o comprimento do arco s ao longo da curva de algum ponto do fio. Esta é uma escolha adequada de coordenada generalizada para o sistema. Apenas uma coordenada é necessária em vez de duas, porque a posição do cordão pode ser parametrizada por um número, s , e a equação de restrição conecta as duas coordenadas x e y ; qualquer um é determinado pelo outro. A força de restrição é a força de reação que o arame exerce sobre o cordão para mantê-lo no arame, e a força não restritiva aplicada é a ação da gravidade sobre o cordão.

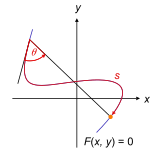
Suponha que o fio mude de forma com o tempo, flexionando. Então, a equação de restrição e a posição da partícula são, respectivamente

{\ displaystyle f (\ mathbf {r}, t) = 0 \ ,, \ quad \ mathbf {r} = (x (s, t), y (s, t))}

que agora ambos dependem do tempo t devido à alteração das coordenadas à medida que o fio muda de forma. Observe que o tempo aparece implicitamente por meio das coordenadas e explicitamente nas equações de restrição.

Pêndulo simples

Pêndulo simples. Como a barra é rígida, a posição do pêndulo é restringida de acordo com a equação f ( x , y ) = 0, a força de restrição C é a tensão na barra. Novamente, a força não restritiva N , neste caso, é a gravidade.

Modelo dinâmico de um pêndulo simples.

A relação entre o uso de coordenadas generalizadas e coordenadas cartesianas para caracterizar o movimento de um sistema mecânico pode ser ilustrada considerando a dinâmica restrita de um pêndulo simples.

Um pêndulo simples consiste em uma massa M pendurada em um ponto de pivô de modo que seja forçada a se mover em um círculo de raio L. A posição da massa é definida pelo vetor de coordenadas r = (x, y) medido no plano de o círculo de modo que y esteja na direção vertical. As coordenadas xey estão relacionadas pela equação do círculo

{\ displaystyle f (x, y) = x ^ {2} + y ^ {2} -L ^ {2} = 0,}

que restringe o movimento de M. Esta equação também fornece uma restrição nos componentes de velocidade,

{\ displaystyle {\ dot {f}} (x, y) = 2x {\ dot {x}} + 2y {\ dot {y}} = 0.}

Agora introduza o parâmetro θ, que define a posição angular de M na direção vertical. Pode ser usado para definir as coordenadas x e y, de modo que

{\ displaystyle \ mathbf {r} = (x, y) = (L \ sin \ theta, -L \ cos \ theta).}

O uso de θ para definir a configuração deste sistema evita a restrição fornecida pela equação do círculo.

Observe que a força da gravidade agindo sobre a massa m é formulada nas coordenadas cartesianas usuais,

{\ displaystyle \ mathbf {F} = (0, -mg),}

onde g é a aceleração da gravidade.

O trabalho virtual da gravidade sobre a massa m conforme segue a trajetória r é dado por

{\ displaystyle \ delta W = \ mathbf {F} \ cdot \ delta \ mathbf {r}.}

A variação r pode ser calculada em termos das coordenadas x e y, ou em termos do parâmetro θ, ${\ displaystyle \ delta}$

{\ displaystyle \ delta \ mathbf {r} = (\ delta x, \ delta y) = (L \ cos \ theta, L \ sin \ theta) \ delta \ theta.}

Assim, o trabalho virtual é dado por

{\ displaystyle \ delta W = -mg \ delta y = -mgL \ sin \ theta \ delta \ theta.}

Observe que o coeficiente de y é o componente y da força aplicada. Da mesma forma, o coeficiente de θ é conhecido como a força generalizada ao longo da coordenada generalizada θ, dada por ${\ displaystyle \ delta}$ ${\ displaystyle \ delta}$

{\ displaystyle F _ {\ theta} = - mgL \ sin \ theta.}

Para completar a análise, considere a energia cinética T da massa, usando a velocidade,

{\ displaystyle \ mathbf {v} = ({\ dot {x}}, {\ dot {y}}) = (L \ cos \ theta, L \ sin \ theta) {\ dot {\ theta}},}

tão,

{\ displaystyle T = {\ frac {1} {2}} m \ mathbf {v} \ cdot \ mathbf {v} = {\ frac {1} {2}} m ({\ dot {x}} ^ { 2} + {\ dot {y}} ^ {2}) = {\ frac {1} {2}} mL ^ {2} {\ dot {\ theta}} ^ {2}.}

A forma de D'Alembert do princípio do trabalho virtual para o pêndulo em termos das coordenadas x e y são dadas por,

{\ displaystyle {\ frac {d} {dt}} {\ frac {\ parcial T} {\ parcial {\ ponto {x}}}} - {\ frac {\ parcial T} {\ parcial x}} = F_ {x} + \ lambda {\ frac {\ partial f} {\ partial x}}, \ quad {\ frac {d} {dt}} {\ frac {\ partial T} {\ partial {\ dot {y} }}} - {\ frac {\ parcial T} {\ parcial y}} = F_ {y} + \ lambda {\ frac {\ parcial f} {\ parcial y}}.}

Isso produz as três equações

{\ displaystyle m {\ ddot {x}} = \ lambda (2x), \ quad m {\ ddot {y}} = - mg + \ lambda (2y), \ quad x ^ {2} + y ^ {2} -L ^ {2} = 0,}

nas três incógnitas, x, y e λ.

Usando o parâmetro θ, essas equações assumem a forma

{\ displaystyle {\ frac {d} {dt}} {\ frac {\ parcial T} {\ parcial {\ ponto {\ theta}}}} - {\ frac {\ parcial T} {\ parcial \ theta}} = F _ {\ theta},}

que se torna,

{\ displaystyle mL ^ {2} {\ ddot {\ theta}} = - mgL \ sin \ theta,}

ou

{\ displaystyle {\ ddot {\ theta}} + {\ frac {g} {L}} \ sin \ theta = 0.}

Esta formulação produz uma equação porque há um único parâmetro e nenhuma equação de restrição.

Isso mostra que o parâmetro θ é uma coordenada generalizada que pode ser usada da mesma forma que as coordenadas cartesianas xey para analisar o pêndulo.

Pêndulo duplo

Um pêndulo duplo

Os benefícios das coordenadas generalizadas tornam-se aparentes com a análise de um pêndulo duplo . Para as duas massas m _i , i = 1, 2, seja r _i = (x _i , y _i ), i = 1, 2 defina suas duas trajetórias. Esses vetores satisfazem as duas equações de restrição,

{\ displaystyle f_ {1} (x_ {1}, y_ {1}, x_ {2}, y_ {2}) = \ mathbf {r} _ {1} \ cdot \ mathbf {r} _ {1} - L_ {1} ^ {2} = 0}

e

{\ displaystyle f_ {2} (x_ {1}, y_ {1}, x_ {2}, y_ {2}) = (\ mathbf {r} _ {2} - \ mathbf {r} _ {1}) \ cdot (\ mathbf {r} _ {2} - \ mathbf {r} _ {1}) - L_ {2} ^ {2} = 0.}

A formulação das equações de Lagrange para este sistema produz seis equações nas quatro coordenadas cartesianas x _i , y _i i = 1, 2 e os dois multiplicadores de Lagrange λ _i , i = 1, 2 que surgem das duas equações de restrição.

Agora introduza as coordenadas generalizadas θ _i i = 1,2 que definem a posição angular de cada massa do pêndulo duplo na direção vertical. Neste caso, temos

{\ displaystyle \ mathbf {r} _ {1} = (L_ {1} \ sin \ theta _ {1}, - L_ {1} \ cos \ theta _ {1}), \ quad \ mathbf {r} _ {2} = (L_ {1} \ sin \ theta _ {1}, - L_ {1} \ cos \ theta _ {1}) + (L_ {2} \ sin \ theta _ {2}, - L_ { 2} \ cos \ theta _ {2}).}

A força da gravidade atuando sobre as massas é dada por,

{\ displaystyle \ mathbf {F} _ {1} = (0, -m_ {1} g), \ quad \ mathbf {F} _ {2} = (0, -m_ {2} g)}

onde g é a aceleração da gravidade. Portanto, o trabalho virtual da gravidade nas duas massas à medida que seguem as trajetórias r _i , i = 1,2 é dado por

{\ displaystyle \ delta W = \ mathbf {F} _ {1} \ cdot \ delta \ mathbf {r} _ {1} + \ mathbf {F} _ {2} \ cdot \ delta \ mathbf {r} _ { 2}.}

As variações δ r _i i = 1, 2 podem ser calculadas para serem

{\ displaystyle \ delta \ mathbf {r} _ {1} = (L_ {1} \ cos \ theta _ {1}, L_ {1} \ sin \ theta _ {1}) \ delta \ theta _ {1} , \ quad \ delta \ mathbf {r} _ {2} = (L_ {1} \ cos \ theta _ {1}, L_ {1} \ sin \ theta _ {1}) \ delta \ theta _ {1} + (L_ {2} \ cos \ theta _ {2}, L_ {2} \ sin \ theta _ {2}) \ delta \ theta _ {2}}

Assim, o trabalho virtual é dado por

{\ displaystyle \ delta W = - (m_ {1} + m_ {2}) gL_ {1} \ sin \ theta _ {1} \ delta \ theta _ {1} -m_ {2} gL_ {2} \ sin \ theta _ {2} \ delta \ theta _ {2},}

e as forças generalizadas são

{\ displaystyle F _ {\ theta _ {1}} = - (m_ {1} + m_ {2}) gL_ {1} \ sin \ theta _ {1}, \ quad F _ {\ theta _ {2}} = -m_ {2} gL_ {2} \ sin \ theta _ {2}.}

Calcule a energia cinética deste sistema para ser

{\ displaystyle T = {\ frac {1} {2}} m_ {1} \ mathbf {v} _ {1} \ cdot \ mathbf {v} _ {1} + {\ frac {1} {2}} m_ {2} \ mathbf {v} _ {2} \ cdot \ mathbf {v} _ {2} = {\ frac {1} {2}} (m_ {1} + m_ {2}) L_ {1} ^ {2} {\ dot {\ theta}} _ {1} ^ {2} + {\ frac {1} {2}} m_ {2} L_ {2} ^ {2} {\ dot {\ theta} } _ {2} ^ {2} + m_ {2} L_ {1} L_ {2} \ cos (\ theta _ {2} - \ theta _ {1}) {\ dot {\ theta}} _ {1 } {\ dot {\ theta}} _ {2}.}

A equação de Euler-Lagrange produz duas equações nas coordenadas generalizadas desconhecidas θ _i i = 1, 2, dadas por

{\ displaystyle (m_ {1} + m_ {2}) L_ {1} ^ {2} {\ ddot {\ theta}} _ {1} + m_ {2} L_ {1} L_ {2} {\ ddot {\ theta}} _ {2} \ cos (\ theta _ {2} - \ theta _ {1}) + m_ {2} L_ {1} L_ {2} {\ ddot {\ theta _ {2}} } ^ {2} \ sin (\ theta _ {1} - \ theta _ {2}) = - (m_ {1} + m_ {2}) gL_ {1} \ sin \ theta _ {1},}

e

{\ displaystyle m_ {2} L_ {2} ^ {2} {\ ddot {\ theta}} _ {2} + m_ {2} L_ {1} L_ {2} {\ ddot {\ theta}} _ { 1} \ cos (\ theta _ {2} - \ theta _ {1}) + m_ {2} L_ {1} L_ {2} {\ ddot {\ theta _ {1}}} ^ {2} \ sin (\ theta _ {2} - \ theta _ {1}) = - m_ {2} gL_ {2} \ sin \ theta _ {2}.}

O uso das coordenadas generalizadas θ _i i = 1, 2 fornece uma alternativa para a formulação cartesiana da dinâmica do pêndulo duplo.

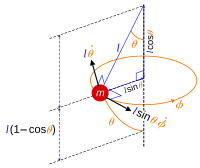
Pêndulo esférico

Pêndulo esférico: ângulos e velocidades.

Para um exemplo 3d, um pêndulo esférico com comprimento constante l livre para oscilar em qualquer direção angular sujeito à gravidade, a restrição no pêndulo pode ser declarada na forma

{\ displaystyle f (\ mathbf {r}) = x ^ {2} + y ^ {2} + z ^ {2} -l ^ {2} = 0 \ ,,}

onde a posição do pêndulo pode ser escrita

{\ displaystyle \ mathbf {r} = (x (\ theta, \ phi), y (\ theta, \ phi), z (\ theta, \ phi)) \ ,,}

em que ( θ , φ ) são os ângulos polares esféricos porque o pêndulo se move na superfície de uma esfera. A posição r é medida ao longo do ponto de suspensão até o pêndulo, aqui tratada como uma partícula pontual . Uma escolha lógica de coordenadas generalizadas para descrever o movimento são os ângulos ( θ , φ ). Apenas duas coordenadas são necessárias em vez de três, porque a posição do pêndulo pode ser parametrizada por dois números, e a equação de restrição conecta as três coordenadas x , y , z para que qualquer uma delas seja determinada a partir das outras duas.

Coordenadas generalizadas e trabalho virtual

O princípio do trabalho virtual estabelece que se um sistema está em equilíbrio estático, o trabalho virtual das forças aplicadas é zero para todos os movimentos virtuais do sistema a partir deste estado, ou seja, W = 0 para qualquer variação r . Quando formulado em termos de coordenadas generalizadas, isso é equivalente ao requisito de que as forças generalizadas para qualquer deslocamento virtual sejam zero, ou seja, F _i = 0. ${\ displaystyle \ delta}$ ${\ displaystyle \ delta}$

Sejam as forças no sistema F _j , j = 1, ..., m aplicadas a pontos com coordenadas cartesianas r _j , j = 1, ..., m, então o trabalho virtual gerado por um deslocamento virtual do posição de equilíbrio é dada por

{\ displaystyle \ delta W = \ sum _ {j = 1} ^ {m} \ mathbf {F} _ {j} \ cdot \ delta \ mathbf {r} _ {j}.}

onde δ r _j , j = 1, ..., m denotam os deslocamentos virtuais de cada ponto do corpo.

Agora suponha que cada δ r _j depende das coordenadas generalizadas q _i , i = 1, ..., n , então

{\ displaystyle \ delta \ mathbf {r} _ {j} = {\ frac {\ partial \ mathbf {r} _ {j}} {\ partial q_ {1}}} \ delta {q} _ {1} + \ ldots + {\ frac {\ partial \ mathbf {r} _ {j}} {\ partial q_ {n}}} \ delta {q} _ {n},}

e

{\ displaystyle \ delta W = \ left (\ sum _ {j = 1} ^ {m} \ mathbf {F} _ {j} \ cdot {\ frac {\ partial \ mathbf {r} _ {j}} { \ partial q_ {1}}} \ right) \ delta {q} _ {1} + \ ldots + \ left (\ sum _ {j = 1} ^ {m} \ mathbf {F} _ {j} \ cdot {\ frac {\ partial \ mathbf {r} _ {j}} {\ partial q_ {n}}} \ right) \ delta {q} _ {n}.}

Os n termos

{\ displaystyle F_ {i} = \ sum _ {j = 1} ^ {m} \ mathbf {F} _ {j} \ cdot {\ frac {\ parcial \ mathbf {r} _ {j}} {\ parcial q_ {i}}}, \ quad i = 1, \ ldots, n,}

são as forças generalizadas que atuam no sistema. Kane mostra que essas forças generalizadas também podem ser formuladas em termos da razão das derivadas do tempo,

{\ displaystyle F_ {i} = \ sum _ {j = 1} ^ {m} \ mathbf {F} _ {j} \ cdot {\ frac {\ parcial \ mathbf {v} _ {j}} {\ parcial {\ dot {q}} _ {i}}}, \ quad i = 1, \ ldots, n,}

onde v _j é a velocidade do ponto de aplicação da força F _j .

Para que o trabalho virtual seja zero para um deslocamento virtual arbitrário, cada uma das forças generalizadas deve ser zero, ou seja

{\ displaystyle \ delta W = 0 \ quad \ Rightarrow \ quad F_ {i} = 0, i = 1, \ ldots, n.}

Veja também

Notas

Referências

^ Ginsberg 2008 , p. 397, §7.2.1 Seleção de coordenadas generalizadas
^ Farid ML Amirouche (2006). "§2.4: Coordenadas generalizadas" . Fundamentos da dinâmica multicorpos: teoria e aplicações . Springer. p. 46. ISBN 0-8176-4236-6.
^ Florian Scheck (2010). "§5.1 Manifolds de coordenadas generalizadas" . Mecânica: Das Leis de Newton ao Caos Determinístico (5ª ed.). Springer. p. 286. ISBN 978-3-642-05369-6.
^ Goldstein 1980 , p. 12
^ ^a ^b Kibble & Berkshire 2004 , p. 232
^ Torby 1984 , p. 260
^ Goldstein 1980 , p. 13
^ Hand & Finch 2008 , p. 15
^ Torby 1984 , p. 269
^ Goldstein 1980 , p. 25
^ Landau & Lifshitz 1976 , p. 8
^ Greenwood, Donald T. (1987). Principles of Dynamics (2ª ed.). Prentice Hall. ISBN 0-13-709981-9.
^ Richard Fitzpatrick, Newtonian Dynamics, http://farside.ph.utexas.edu/teaching/336k/Newton/Newtonhtml.html .
^ Eric W. Weisstein, pêndulo duplo , scienceworld.wolfram.com. 2007
^ Torby, Bruce (1984). "Métodos de energia". Dinâmica avançada para engenheiros . Série HRW em Engenharia Mecânica. Estados Unidos da América: CBS College Publishing. ISBN 0-03-063366-4.
^ TR Kane e DA Levinson, Dynamics: teoria e aplicações, McGraw-Hill, New York, 1985

Bibliografia de referências citadas

Ginsberg, Jerry H. (2008). Dinâmica de engenharia (3ª ed.). Cambridge UK: Cambridge University Press . ISBN 978-0-521-88303-0.
Kibble, TWB ; Berkshire, FH (2004). Mecânica Clássica (5ª ed.). River Edge NJ: Imperial College Press . ISBN 1860944248.

[Ginsberg-1] Ginsberg 2008 , p. 397, §7.2.1 Seleção de coordenadas generalizadas

[Amirouche-2] Farid ML Amirouche (2006). "§2.4: Coordenadas generalizadas" . Fundamentos da dinâmica multicorpos: teoria e aplicações . Springer. p. 46. ISBN 0-8176-4236-6.

[Scheck-3] Florian Scheck (2010). "§5.1 Manifolds de coordenadas generalizadas" . Mecânica: Das Leis de Newton ao Caos Determinístico (5ª ed.). Springer. p. 286. ISBN 978-3-642-05369-6.

[4] Goldstein 1980 , p. 12

[Kibble_2004_page=232-6] Kibble & Berkshire 2004 , p. 232

[7] Torby 1984 , p. 260

[8] Goldstein 1980 , p. 13

[Hand_2008_page=15-9] Hand & Finch 2008 , p. 15

[Torby_1984_page=269-11] Torby 1984 , p. 269

[12] Goldstein 1980 , p. 25

[13] Landau & Lifshitz 1976 , p. 8

[14] Greenwood, Donald T. (1987). Principles of Dynamics (2ª ed.). Prentice Hall. ISBN 0-13-709981-9.

[15] Richard Fitzpatrick, Newtonian Dynamics, http://farside.ph.utexas.edu/teaching/336k/Newton/Newtonhtml.html .

[16] Eric W. Weisstein, pêndulo duplo , scienceworld.wolfram.com. 2007

[Torby1984-17] Torby, Bruce (1984). "Métodos de energia". Dinâmica avançada para engenheiros . Série HRW em Engenharia Mecânica. Estados Unidos da América: CBS College Publishing. ISBN 0-03-063366-4.

[18] TR Kane e DA Levinson, Dynamics: teoria e aplicações, McGraw-Hill, New York, 1985

Languages

In other projects