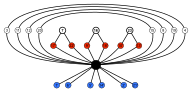
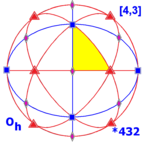
Simetria octaédrica - Octahedral symmetry

Grupos de pontos em três dimensões
Grupo poliédrico , [n, 3], (* n32)
Simetria involucional C _s , (*) [] =	Simetria cíclica C _nv , (* nn) [n] =	Simetria diedral D _nh , (* n22) [n, 2] =
Simetria tetraédrica T _d , (* 332) [3,3] =	Simetria octaédrica O _h , (* 432) [4,3] =	Simetria icosaédrica I _h , (* 532) [5,3] =

Gráfico de ciclo
Os quatro ciclos hexagonais têm a inversão (o nó preto no topo) em comum. Os hexágonos são simétricos, então, por exemplo, 3 e 4 estão no mesmo ciclo.

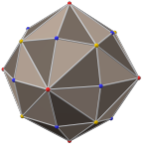
Um octaedro regular tem 24 simetrias rotacionais (ou que preservam a orientação) e 48 simetrias ao todo. Isso inclui transformações que combinam um reflexo e uma rotação. Um cubo tem o mesmo conjunto de simetrias, uma vez que é o poliedro que é dual a um octaedro.

O grupo de simetrias que preservam a orientação é S ₄ , o grupo simétrico ou o grupo de permutações de quatro objetos, uma vez que existe exatamente uma tal simetria para cada permutação das quatro diagonais do cubo.

Detalhes

Simetria octaédrica quiral e completa (ou aquiral ) são as simetrias de ponto discreto (ou equivalentemente, simetrias na esfera ) com os maiores grupos de simetria compatíveis com a simetria translacional . Eles estão entre os grupos de pontos cristalográficos do sistema de cristal cúbico .

Aulas de conjugação
Elementos de O		Inversões de elementos de O
identidade	0	inversão	0 '
3 × rotação de 180 ° em torno de um eixo de 4 vezes	7, 16, 23	3 × reflexão em um plano perpendicular a um eixo de 4 vezes	7 ', 16', 23 '
8 × rotação de 120 ° em torno de um eixo triplo	3, 4, 8, 11, 12, 15, 19, 20	8 × rotoreflection em 60 °	3 ', 4', 8 ', 11', 12 ', 15', 19 ', 20'
6 × rotação de 180 ° em torno de um eixo de 2 vezes	1 ', 2', 5 ', 6', 14 ', 21'	6 × reflexão em um plano perpendicular a um eixo de 2 dobras	1, 2, 5, 6, 14, 21
6 × rotação de 90 ° em torno de um eixo de 4 vezes	9 ', 10', 13 ', 17', 18 ', 22'	6 × rotorreflecção em 90 °	9, 10, 13, 17, 18, 22

Exemplos
${\ displaystyle (0,0) = 0}$	${\ displaystyle (3,0) = 7}$	${\ displaystyle (0,3) = 3}$	${\ displaystyle (7,1) = 1 '}$	${\ displaystyle (4,5) = 9 '}$
${\ displaystyle (7,0) = 0 '}$	${\ displaystyle (4,0) = 7 '}$	${\ displaystyle (7,3) = 3 '}$	${\ displaystyle (0,1) = 1}$	${\ displaystyle (3,5) = 9}$
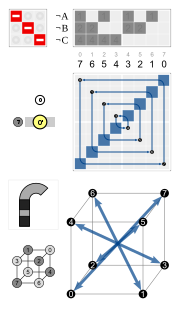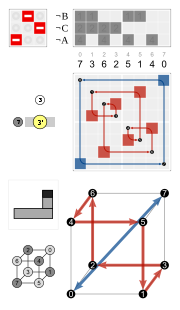Uma lista completa pode ser encontrada no artigo da Wikiversidade .

Como o grupo hiperoctaédrico de dimensão 3, o grupo octaédrico completo é o produto da coroa , e uma maneira natural de identificar seus elementos é como pares com e . Mas como também é o produto direto , pode-se simplesmente identificar os elementos do subgrupo tetraédrico T _d as e suas inversões as . ${\ displaystyle S_ {2} \ wr S_ {3} \ simeq S_ {2} ^ {3} \ rtimes S_ {3}}$
${\ displaystyle (m, n)}$ ${\ displaystyle m \ in [0,2 ^ {3})}$ ${\ displaystyle n \ in [0,3!)}$
${\ displaystyle S_ {4} \ vezes S_ {2}}$ ${\ displaystyle a \ in [0,4!)}$ ${\ displaystyle a '}$

Assim, por exemplo, a identidade é representada como e a inversão como . é representado como e como . ${\ displaystyle (0,0)}$ ${\ displaystyle 0}$ ${\ displaystyle (7,0)}$ ${\ displaystyle 0 '}$
${\ displaystyle (3,1)}$ ${\ displaystyle 6}$ ${\ displaystyle (4,1)}$ ${\ displaystyle 6 '}$

Uma rotorreflecção é uma combinação de rotação e reflexão.

Ilustração de rotorreflecções
A reflexão ${\ displaystyle 7 '}$ aplicado na rotação de 120 ° ${\ displaystyle 4}$ dá a rotorreflecção de 60 ° . ${\ displaystyle 8 '}$ ${\ displaystyle 7 '\ circ 4 = 8'}$
A reflexão ${\ displaystyle 7 '}$ aplicado na rotação de 90 ° ${\ displaystyle 22 '}$ dá a rotorreflecção de 90 ° . ${\ displaystyle 17}$ ${\ displaystyle 7 '\ circ 22' = 17}$

Simetria octaédrica quiral

Eixos giratórios
C ₄	C ₃	C ₂
3	4	6

O , 432 ou [4,3] ⁺ da ordem 24, é simetria octaédrica quiral ou simetria octaédrica rotacional . Este grupo é como a simetria tetraédrica quiral T , mas os eixos C ₂ agora são eixos C ₄ e, adicionalmente, há 6 eixos C ₂ , através dos pontos médios das arestas do cubo. T _d e O são isomórficos como grupos abstratos: ambos correspondem a S ₄ , o grupo simétrico em 4 objetos. T _d é a união de T e o conjunto obtido pela combinação de cada elemento de O \ T com inversão. O é o grupo de rotação do cubo e o octaedro regular .

Simetria octaédrica quiral
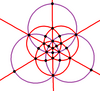
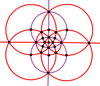
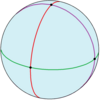
Projeção ortogonal	Projeção estereográfica
2 vezes	4 vezes	3 vezes	2 vezes

Simetria octaédrica completa

O _h , * 432 , [4,3], ou m3m da ordem 48 - simetria octaédrica aquiral ou simetria octaédrica completa . Este grupo tem os mesmos eixos de rotação que O , mas com planos espelhados, compreendendo ambos os planos espelhados de T _d e T _h . Este grupo é isomórfico a S ₄ . C ₂ , e é o grupo de simetria completo do cubo e do octaedro . É o grupo hiperoctaédrico para n = 3. Veja também as isometrias do cubo .

Composto de cubo e octaedro

Cada face do dodecaedro disdyakis é um domínio fundamental.

O grupo octaédrico O _h com domínio fundamental

Com os eixos quádruplos como eixos coordenados, um domínio fundamental de O _h é dado por 0 ≤ x ≤ y ≤ z . Um objeto com esta simetria é caracterizado pela parte do objeto no domínio fundamental, por exemplo, o cubo é dado por z = 1, e o octaedro por x + y + z = 1 (ou as desigualdades correspondentes, para obter o sólido em vez da superfície). ax + by + cz = 1 dá um poliedro com 48 faces, por exemplo, o dodecaedro disdyakis.

As faces são 8 por 8 combinadas com faces maiores para a = b = 0 (cubo) e 6 por 6 para a = b = c (octaedro).

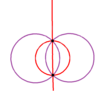
As 9 linhas espelhadas de simetria octaédrica completa podem ser divididas em dois subgrupos de 3 e 6 (desenhados em roxo e vermelho), representando em duas subsimetrias ortogonais: D _2h e T _d . A simetria D _2h pode ser duplicada para D _4h restaurando 2 espelhos de uma das três orientações.

Simetria octaédrica e subgrupos reflexivos

Projeção ortográfica	Projeção estereográfica
Projeção ortográfica	4 vezes	3 vezes	2 vezes
O _h , [4,3],, simetria octaédrica completa (3 + 6 espelhos)

T _d , [3,3] = [1 ⁺ , 4,3], = , subgrupo tetraédrico (6 espelhos)

C _3v , [3],, subgrupo diédrico (3 espelhos)

Projeção ortográfica	Projeção estereográfica
Projeção ortográfica	4 vezes	3 vezes	2 vezes
D _4h , [4,2], subgrupo diédrico (1 + 2 + 2 espelhos)

D _2h , [2,2] = [4,3 *], = subgrupo diédrico (1 + 1 + 1 espelhos)

C _4v , [4],, subgrupo diédrico (2 + 2 espelhos)

Matrizes de rotação

Pegue o conjunto de todas as matrizes de permutação 3x3 e atribua um sinal + ou um sinal - a cada um dos três 1s. Existem 6 permutações x 8 combinações de sinais = 48 matrizes no total, dando o grupo octaédrico completo. Existem exatamente 24 matrizes com determinante = +1 e essas são as matrizes de rotação do grupo octaédrico quiral. As outras 24 matrizes correspondem a uma reflexão ou inversão.

Três matrizes geradoras refletivas são necessárias para a simetria octaédrica, que representam os três espelhos de um diagrama de Coxeter-Dynkin . O produto das reflexões produz 3 geradores rotacionais.

[4,3],
	Reflexões			Rotações			Rotorreflecção
Geradores	R ₀	R ₁	R ₂	R ₀ R ₁	R ₁ R ₂	R ₀ R ₂	R ₀ R ₁ R ₂
Grupo
Pedido	2	2	2	4	3	2	6
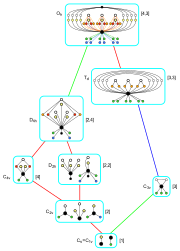
Matriz	${\ displaystyle \ left [{\ begin {smallmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\\ end {smallmatrix}} \ right]}$	${\ displaystyle \ left [{\ begin {smallmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\\ end {smallmatrix}} \ right]}$	${\ displaystyle \ left [{\ begin {smallmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\\ end {smallmatrix}} \ right]}$	${\ displaystyle \ left [{\ begin {smallmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \\\ end {smallmatrix}} \ right]}$	${\ displaystyle \ left [{\ begin {smallmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\\ end {smallmatrix}} \ right]}$	${\ displaystyle \ left [{\ begin {smallmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & -1 \\\ end {smallmatrix}} \ right]}$	${\ displaystyle \ left [{\ begin {smallmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ - 1 & 0 & 0 \\\ end {smallmatrix}} \ right]}$

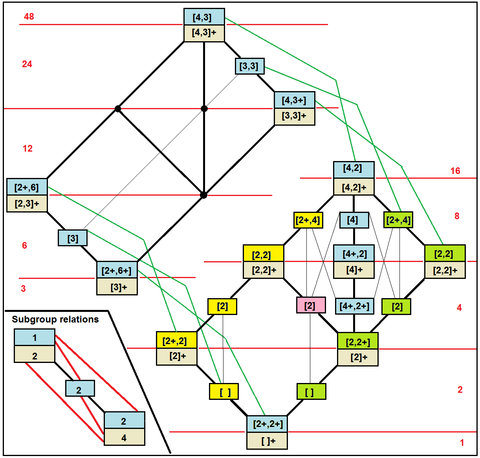
Subgrupos de simetria octaédrica completa

O

T _d

T _h

Gráficos de ciclo de subgrupos de ordem 24

Subgrupos ordenados em um diagrama de Hasse

Subgrupos de rotação

Subgrupos reflexivos

Subgrupos contendo inversão

Schoe.	Coxeter	Esfera.	HM	Estrutura	Pedido	Índice
O _h	[4,3]	* 432	m 3 m	S ₄ × S ₂	48	1
T _d	[3,3]	* 332	4 3m	S ₄	24	2
D _4h	[2,4]	* 224	4 / mmm	D ₂ × D ₈	16	3
D _2h	[2,2]	* 222	mmm	D ₂³ = D ₂ × D ₄	8	6
C _4v	[4]	* 44	4mm	D ₈	8	6
C _3v	[3]	* 33	3m	D ₆ = S ₃	6	8
C _2v	[2]	* 22	mm2	D ₂² = D ₄	4	12
C _s = C _1v	[]	*	2 ou m	D ₂	2	24
T _h	[3 ⁺ , 4]	3 * 2	m 3	A ₄ × S ₂	24	2
C _4h	[4 ⁺ , 2]	4 *	4 / m	Z ₄ × D ₂	8	6
D _3d	[2 ⁺ , 6]	2 * 3	3 m	D ₁₂ = Z ₂ × D ₆	12	4
D _2d	[2 ⁺ , 4]	2 * 2	4 2m	D ₈	8	6
C _2h = D _1d	[2 ⁺ , 2]	2 *	2 / m	Z ₂ × D ₂	4	12
S ₆	[2 ⁺ , 6 ⁺ ]	3 ×	3	Z ₆ = Z ₂ × Z ₃	6	8
S ₄	[2 ⁺ , 4 ⁺ ]	2 ×	4	Z ₄	4	12
S ₂	[2 ⁺ , 2 ⁺ ]	×	1	S ₂	2	24
O	[4,3] ⁺	432	432	S ₄	24	2
T	[3,3] ⁺	332	23	A ₄	12	4
D ₄	[2,4] ⁺	224	422	D ₈	8	6
D ₃	[2,3] ⁺	223	322	D ₆ = S ₃	6	8
D ₂	[2,2] ⁺	222	222	D ₄ = Z ₂²	4	12
C ₄	[4] ⁺	44	4	Z ₄	4	12
C ₃	[3] ⁺	33	3	Z ₃ = A ₃	3	16
C ₂	[2] ⁺	22	2	Z ₂	2	24
C ₁	[] ⁺	11	1	Z ₁	1	48

Subgrupos octaédricos na notação de Coxeter

As isometrias do cubo

48 elementos de simetria de um cubo

O cubo possui 48 isometrias (elementos de simetria), formando o grupo de simetria O _h , isomorfo a S ₄ × Z ₂ . Eles podem ser categorizados da seguinte forma:

O (a identidade e 23 rotações adequadas) com as seguintes classes de conjugação (entre parênteses são dadas as permutações das diagonais do corpo e a representação do quatérnio unitário ):
- identidade (identidade; 1)
- rotação em torno de um eixo do centro de uma face para o centro da face oposta por um ângulo de 90 °: 3 eixos, 2 por eixo, juntos 6 ((1 2 3 4), etc .; ((1 ± i ) / √ 2 , etc.)
- idem por um ângulo de 180 °: 3 eixos, 1 por eixo, juntos 3 ((1 2) (3 4), etc .; i , j , k )
- rotação em torno de um eixo do centro de uma borda ao centro da borda oposta por um ângulo de 180 °: 6 eixos, 1 por eixo, juntos 6 ((1 2), etc .; (( i ± j ) / √ 2 , etc.)
- rotação em torno de uma diagonal do corpo por um ângulo de 120 °: 4 eixos, 2 por eixo, juntos 8 ((1 2 3), etc.; (1 ± i ± j ± k ) / 2)
O mesmo com a inversão ( x é mapeado para - x ) (também 24 isometrias). Observe que a rotação por um ângulo de 180 ° em torno de um eixo combinado com a inversão é apenas uma reflexão no plano perpendicular. A combinação de inversão e rotação em torno de uma diagonal do corpo por um ângulo de 120 ° é a rotação em torno da diagonal do corpo por um ângulo de 60 °, combinada com a reflexão no plano perpendicular (a própria rotação não mapeia o cubo para si mesma; a interseção do plano de reflexão com o cubo é um hexágono regular ).

Uma isometria do cubo pode ser identificada de várias maneiras:

pelas faces três faces adjacentes dadas (digamos 1, 2 e 3 em um dado) são mapeadas para
pela imagem de um cubo com em uma das faces uma marcação não simétrica: a face com a marcação, seja ela normal ou uma imagem espelhada, e a orientação
por uma permutação das quatro diagonais do corpo (cada uma das 24 permutações é possível), combinada com um alternador para inversão do cubo, ou não

Para cubos com cores ou marcações (como os dados têm), o grupo de simetria é um subgrupo de O _h .

Exemplos:

C _{4 v} , [4], (* 422): se uma face tem uma cor diferente (ou duas faces opostas têm cores diferentes uma da outra e das outras quatro), o cubo tem 8 isometrias, como um quadrado tem em 2D .
D _{2 h} , [2,2], (* 222): se faces opostas têm as mesmas cores, diferentes para cada conjunto de dois, o cubo tem 8 isometrias, como um cuboide .
D _{4 h} , [4,2], (* 422): se duas faces opostas têm a mesma cor, e todas as outras faces têm uma cor diferente, o cubo tem 16 isometrias, como um prisma quadrado (caixa quadrada).
C _{2 v} , [2], (* 22):
- se duas faces adjacentes têm a mesma cor e todas as outras faces têm uma cor diferente, o cubo tem 4 isometrias.
- se três faces, das quais duas opostas uma à outra, têm uma cor e as outras três uma outra cor, o cubo tem 4 isometrias.
- se duas faces opostas têm a mesma cor, e duas outras faces opostas também, e as duas últimas têm cores diferentes, o cubo tem 4 isometrias, como um pedaço de papel em branco com uma forma com simetria espelhada.
C _s , [], (*):
- se duas faces adjacentes têm cores diferentes uma da outra e as outras quatro têm uma terceira cor, o cubo tem 2 isometrias.
- se duas faces opostas têm a mesma cor e todas as outras faces têm cores diferentes, o cubo tem 2 isometrias, como uma folha assimétrica de papel em branco.
C _{3 v} , [3], (* 33): se três faces, nenhuma das quais opostas uma à outra, têm uma cor e as outras três uma outra cor, o cubo tem 6 isometrias.

Para alguns subgrupos maiores, um cubo com esse grupo como grupo de simetria não é possível apenas colorindo faces inteiras. É preciso desenhar algum padrão nos rostos.

Exemplos:

D _{2 d} , [2 ⁺ , 4], (2 * 2): se uma face tem um segmento de linha dividindo a face em dois retângulos iguais, e o oposto tem o mesmo na direção perpendicular, o cubo tem 8 isometrias; há um plano de simetria e simetria rotacional de 2 vezes com um eixo em um ângulo de 45 ° em relação a esse plano e, como resultado, há também outro plano de simetria perpendicular ao primeiro e outro eixo de simetria de rotação de 2 vezes perpendicular ao primeiro.
T _h , [3 ⁺ , 4], (3 * 2): se cada face tiver um segmento de linha dividindo a face em dois retângulos iguais, de modo que os segmentos de linha das faces adjacentes não se encontrem na aresta, o cubo tem 24 isometrias: as permutações pares das diagonais do corpo e as mesmas combinadas com a inversão ( x é mapeado para - x ).
T _d , [3,3], (* 332): se o cubo consiste em oito cubos menores, quatro brancos e quatro pretos, colocados juntos alternadamente em todas as três direções padrão, o cubo tem novamente 24 isometrias: desta vez, as permutações pares das diagonais do corpo e os inversos das outras rotações próprias.
T , [3,3] ⁺ , (332): se cada face tem o mesmo padrão com simetria rotacional de 2 dobras, digamos a letra S, de modo que em todas as bordas um topo de um S encontra um lado do outro S, o cubo tem 12 isometrias: as permutações pares das diagonais do corpo.

A simetria total do cubo, O _h , [4,3], (* 432), é preservada se e somente se todas as faces têm o mesmo padrão de tal forma que a simetria total do quadrado é preservada, com para o quadrado uma simetria grupo, Dih ₄ , [4], da ordem 8.

A simetria completa do cubo sob rotações adequadas, O , [4,3] ⁺ , (432), é preservada se e somente se todas as faces têm o mesmo padrão com simetria rotacional de 4 vezes , Z ₄ , [4] ⁺ .

Simetria octaédrica da superfície Bolza

Na teoria da superfície de Riemann , a superfície de Bolza , às vezes chamada de curva de Bolza, é obtida como a cobertura dupla ramificada da esfera de Riemann, com locus de ramificação no conjunto de vértices do octaedro inscrito regular. Seu grupo de automorfismo inclui a involução hiperelíptica que vira as duas folhas da capa. O quociente pelo subgrupo de ordem 2 gerado pela involução hiperelíptica produz precisamente o grupo de simetrias do octaedro. Entre as muitas propriedades notáveis da superfície Bolza está o fato de que ela maximiza a sístole entre todas as superfícies hiperbólicas do gênero 2.

Sólidos com simetria quiral octaédrica

Classe	Nome	Foto	Rostos	Arestas	Vértices	Nome duplo	Foto
Sólido arquimediano ( sólido catalão )	cubo arrebitado		38	60	24	icositraedro pentagonal

Sólidos com simetria octaédrica completa

Classe	Nome	Rostos	Arestas	Vértices	Nome duplo
Sólido platônico	Cubo	6	12	8	Octaedro
Sólido arquimediano ( sólido catalão duplo )	Cuboctaedro	14	24	12	Dodecaedro rômbico
	Cubo truncado	14	36	24	Octaedro triakis
	Octaedro truncado	14	36	24	Hexaedro de Tetrakis
	Rombicuboctaedro	26	48	24	Icositetraedro deltóide
	Cuboctaedro truncado	26	72	48	Dodecaedro de Disdyakis
Regular composto poliedro	Stella octangula	8	12	8	Autoduplicado
Regular composto poliedro	Cubo e octaedro	14	24	14	Autoduplicado

Veja também

Simetria tetraédrica
Simetria icosaédrica
Grupo octaédrico binário
Grupo hiperoctaédrico
Materiais de aprendizagem relacionados ao grupo octaédrico completo na Wikiversidade

Referências

Peter R. Cromwell, Polyhedra (1997), p. 295
The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5
Kaleidoscopes: Selected Writings of HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
NW Johnson : Geometries and Transformations , (2018) ISBN 978-1-107-10340-5 Capítulo 11: Grupos de simetria finita , 11,5 grupos de Coxeter esféricos

links externos

Weisstein, Eric W. "Octahedral group" . MathWorld .
Groupprops: produto direto de S4 e Z2

Languages

In other projects