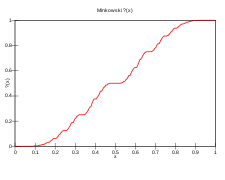
Racional diádico - Dyadic rational

Racionais diádicos no intervalo de 0 a 1

Em matemática, um racional diádico ou racional binário é um número que pode ser expresso como uma fração cujo denominador é uma potência de dois . Por exemplo, 1/2, 3/2 e 3/8 são racionais diádicos, mas 1/3 não é. Esses números são importantes na ciência da computação porque são os únicos com representações binárias finitas . Os racionais diádicos também têm aplicações em pesos e medidas, compassos musicais e educação matemática inicial. Eles podem aproximar com precisão qualquer número real .

A soma, diferença ou produto de quaisquer dois números racionais diádicos é outro número racional diádico, dado por uma fórmula simples. No entanto, a divisão de um número racional diádico por outro nem sempre produz um resultado racional diádico. Matematicamente, isso significa que os números racionais diádicos formam um anel , situando-se entre o anel dos inteiros e o campo dos números racionais . Este anel pode ser denotado . ${\ displaystyle \ mathbb {Z} [{\ tfrac {1} {2}}]}$

Em matemática avançada, os números racionais diádicos são centrais para as construções do solenóide diádico , a função de ponto de interrogação de Minkowski , as ondas de Daubechies , o grupo de Thompson , Prüfer 2-grupo , números surreais e números fusíveis . Esses números são de ordem isomórfica aos números racionais; eles formam um subsistema dos números 2-ádicos , bem como dos reais, e podem representar as partes fracionárias dos números 2-ádicos. Funções de números naturais a racionais diádicos têm sido usadas para formalizar a análise matemática em matemática reversa .

Formulários

Em medição

Pesos de cozinha medindo frações diádicas de uma libra de 2 lb a 1/64 lb (1/4 oz)

Muitos sistemas tradicionais de pesos e medidas são baseados na ideia de divisão repetida pela metade, o que produz racionais diádicos ao medir quantidades fracionárias de unidades. A polegada é habitualmente subdividida em racionais diádicos em vez de usar uma subdivisão decimal. As divisões habituais do galão em meias galões, quarts , pintas e copos também são dyadic. Os antigos egípcios usavam racionais diádicos na medição, com denominadores de até 64. Da mesma forma, os sistemas de pesos da Civilização do Vale do Indo são em sua maioria baseados em repetidas reduções pela metade; a antropóloga Heather M.-L. Miller escreve que "reduzir pela metade é uma operação relativamente simples com balanços de viga, o que é provavelmente porque tantos sistemas de peso deste período usavam sistemas binários".

Em computação

Racionais diádicos são centrais para a ciência da computação como um tipo de número fracionário que muitos computadores podem manipular diretamente. Em particular, como um tipo de dados usado por computadores, os números de ponto flutuante são freqüentemente definidos como inteiros multiplicados por potências positivas ou negativas de dois. Os números que podem ser representados precisamente em um formato de ponto flutuante, como os tipos de dados de ponto flutuante IEEE , são chamados de números representáveis. Para a maioria das representações de ponto flutuante, os números representáveis ​​são um subconjunto dos racionais diádicos. O mesmo é verdadeiro para tipos de dados de ponto fixo , que também usam potências de dois implicitamente na maioria dos casos. Devido à simplicidade da computação com racionais diádicos, eles também são usados ​​para computação real exata usando aritmética de intervalo e são centrais para alguns modelos teóricos de números computáveis .

Gerar uma variável aleatória a partir de bits aleatórios, em um período fixo de tempo, só é possível quando a variável tem um número finito de resultados cujas probabilidades são todos números racionais diádicos. Para variáveis ​​aleatórias cujas probabilidades não são diádicas, é necessário aproximar suas probabilidades por racionais diádicos ou usar um processo de geração aleatória cujo tempo é ele próprio aleatório e ilimitado.

Na música

Cinco compassos de A Sagração da Primavera, de Igor Stravinski , mostrando sinais de tempo
³
₁₆, ²
₁₆, ³
₁₆, e ²
₈

As assinaturas de tempo na notação musical ocidental são tradicionalmente escritas em uma forma semelhante a frações (por exemplo:²
₂, ⁴
₄, ou ⁶
₈), embora a linha horizontal da pauta musical que separa o número superior e inferior seja geralmente omitida ao escrever a assinatura separadamente de sua pauta. Como frações, eles são geralmente diádicos, embora assinaturas de tempo não diádicas também tenham sido usadas. O valor numérico da assinatura, interpretado como uma fração, descreve o comprimento de um compasso como uma fração de uma nota inteira . Seu numerador descreve o número de batidas por compasso e o denominador descreve a duração de cada batida.

Na educação matemática

Nas teorias do desenvolvimento infantil do conceito de fração com base na obra de Jean Piaget , os números fracionários decorrentes da redução pela metade e repetidas pela metade estão entre as primeiras formas de frações a se desenvolver. Este estágio de desenvolvimento do conceito de frações foi denominado "divisão algorítmica". A adição e subtração desses números podem ser realizadas em etapas que envolvem apenas dobrar, dividir pela metade, somar e subtrair inteiros. Em contraste, a adição e subtração de frações mais gerais envolve multiplicação e fatoração de inteiros para chegar a um denominador comum. Portanto, as frações diádicas podem ser mais fáceis para os alunos calcularem do que com frações mais gerais.

Definições e aritmética

Os números diádicos são os números racionais que resultam da divisão de um inteiro por uma potência de dois . Um número racional em termos mais simples é um racional diádico quando é uma potência de dois. Outra maneira equivalente de definir os racionais diádicos é que eles são os números reais que têm uma representação binária final . ${\ displaystyle p / q}$${\ displaystyle q}$

A adição , subtração e multiplicação de quaisquer dois racionais diádicos produzem outro racional diádico, de acordo com as seguintes fórmulas:

${\ displaystyle {\ begin {align} {\ frac {a} {2 ^ {b}}} + {\ frac {c} {2 ^ {d}}} & = {\ frac {2 ^ {d- \ min (b, d)} a + 2 ^ {b- \ min (b, d)} c} {2 ^ {\ max (b, d)}}} \\ [6px] {\ frac {a} { 2 ^ {b}}} - {\ frac {c} {2 ^ {d}}} & = {\ frac {2 ^ {d- \ min (b, d)} a-2 ^ {b- \ min (b, d)} c} {2 ^ {\ max (b, d)}}} \\ [6px] {\ frac {a} {2 ^ {b}}} \ cdot {\ frac {c} { 2 ^ {d}}} & = {\ frac {ac} {2 ^ {b + d}}} \ end {alinhado}}}$

No entanto, o resultado da divisão de um racional diádico por outro não é necessariamente um racional diádico. Por exemplo, 1 e 3 são ambos números racionais diádicos, mas 1/3 não é.

Propriedades adicionais

Aproximações racionais diádicas da raiz quadrada de 2 ( ), encontradas arredondando-se para o múltiplo inteiro menor mais próximo de para A altura da região rosa acima de cada aproximação é seu erro.${\ displaystyle {\ sqrt {2}} \ approx 1,4142}$${\ displaystyle 1/2 ^ {i}}$${\ displaystyle i = 0,1,2, \ dots}$

Números reais sem aproximações racionais diádicas excepcionalmente precisas. Os círculos vermelhos circundam os números cujo erro é aproximado por . Para números no fractal Cantor definidos fora dos círculos, todas as aproximações racionais diádicas têm erros maiores.${\ displaystyle {\ tfrac {1} {6}} / 2 ^ {i}}$${\ displaystyle n / 2 ^ {i}}$

Cada inteiro, e cada meio-inteiro , é um racional diádico. Ambos atendem à definição de ser um inteiro dividido por uma potência de dois: todo inteiro é um inteiro dividido por um (a potência zero de dois), e cada meio-inteiro é um inteiro dividido por dois.

Cada número real pode ser aproximado arbitrariamente por racionais diádicos. Em particular, para um número real , considere os racionais diádicos da forma , onde pode ser qualquer número inteiro e denota a função de base que arredonda seu argumento para um número inteiro. Esses números aproximam-se de baixo para dentro de um erro de , que pode ser arbitrariamente pequeno ao escolher ser arbitrariamente grande. Para um subconjunto fractal de números reais, esse limite de erro está dentro de um fator constante de ótimo: para esses números, não há aproximação com erro menor do que uma constante . A existência de aproximações diádicas precisas pode ser expressa dizendo que o conjunto de todos os racionais diádicos é um denso na linha real . Mais fortemente, este conjunto é uniformemente denso, no sentido de que os racionais diádicos com denominador estão uniformemente espaçados na linha real. ${\ displaystyle x}$${\ textstyle \ lfloor 2 ^ {i} x \ rfloor / 2 ^ {i}}$${\ displaystyle i}$${\ displaystyle \ lfloor \ dots \ rfloor}$${\ displaystyle x}$${\ displaystyle 1/2 ^ {i}}$${\ displaystyle i}$${\ displaystyle n / 2 ^ {i}}$${\ displaystyle 1/2 ^ {i}}$${\ displaystyle 2 ^ {i}}$

Os racionais diádicos são precisamente aqueles números que possuem expansões binárias finitas . Suas expansões binárias não são únicas; há uma representação finita e uma infinita de cada racional diádico diferente de 0 (ignorando o terminal 0s). Por exemplo, 0,11 ₂ = 0,10111 ... ₂ , dando duas representações diferentes para 3/4. Os racionais diádicos são os únicos números cujas expansões binárias não são únicas.

Em matemática avançada

Estrutura algébrica

Por serem fechados sob adição, subtração e multiplicação, mas não divisão, os racionais diádicos são um anel, mas não um campo . O anel de racionais diádicos pode ser denotado , o que significa que pode ser gerado avaliando polinômios com coeficientes inteiros, no argumento 1/2. Como um anel, os racionais diádicos são um subanel dos números racionais e um overring dos inteiros. Algebricamente, esse anel é a localização dos inteiros em relação ao conjunto de potências de dois . ${\ displaystyle \ mathbb {Z} [{\ tfrac {1} {2}}]}$

Além de formar um subanel dos números reais , os números racionais diádicos formam um subanel dos números 2-ádicos , um sistema de números que pode ser definido a partir de representações binárias que são finitas à direita do ponto binário, mas podem se estender infinitamente longe para a esquerda. Os números 2-ádicos incluem todos os números racionais, não apenas os racionais diádicos. Incorporar os racionais diádicos aos números 2-ádicos não muda a aritmética dos racionais diádicos, mas lhes dá uma estrutura topológica diferente daquela que têm como um subanel dos números reais. Como fazem nos reais, os racionais diádicos formam um subconjunto denso dos números 2-ádicos e são o conjunto de números 2-ádicos com expansões binárias finitas. Cada número 2-ádico pode ser decomposto na soma de um inteiro 2-ádico e um racional diádico; nesse sentido, os racionais diádicos podem representar as partes fracionárias de números 2-ádicos, mas essa decomposição não é única.

A adição dos racionais diádicos módulo 1 (o grupo quociente dos racionais diádicos pelos inteiros) forma o grupo 2 de Prüfer . ${\ displaystyle \ mathbb {Z} [{\ tfrac {1} {2}}] / \ mathbb {Z}}$

Solenóide diádico

Considerar apenas as operações de adição e subtração dos racionais diádicos dá-lhes a estrutura de um grupo abeliano aditivo . A dualidade de Pontryagin é um método de compreensão de grupos abelianos por meio da construção de grupos duais, cujos elementos são personagens do grupo original, homomorfismos de grupo ao grupo multiplicativo dos números complexos , com multiplicação pontual como operação de grupo dual. O grupo dual dos racionais diádicos aditivos, assim construído, também pode ser visto como um grupo topológico . É chamado de solenóide diádico e é isomórfico ao produto topológico dos números reais e números 2-ádicos, quociente pela incorporação diagonal dos racionais diádicos neste produto. É um exemplo de um protorus , um solenóide e um continuum indecomponível .

Funções com racionais diádicos como pontos distintos

A função de ponto de interrogação de Minkowski mapeia números racionais para racionais diádicos

Uma onda de Daubechies , mostrando pontos de não suavidade em racionais diádicos

Por serem um subconjunto denso dos números reais, os racionais diádicos, com sua ordenação numérica, formam uma ordem densa . Como acontece com quaisquer duas ordens lineares densas contáveis ​​ilimitadas, pelo teorema do isomorfismo de Cantor , os racionais diádicos são isomórficos de ordem em relação aos números racionais. Nesse caso, a função de ponto de interrogação de Minkowski fornece uma bijeção que preserva a ordem entre o conjunto de todos os números racionais e o conjunto de racionais diádicos.

Os racionais diádicos desempenham um papel fundamental na análise das wavelets de Daubechies , pois o conjunto de pontos onde a função de escala dessas wavelets não é suave. Da mesma forma, os racionais diádicos parametrizam as descontinuidades na fronteira entre os pontos estáveis ​​e instáveis ​​no espaço de parâmetros do mapa de Hénon .

O conjunto de homeomorfismos lineares por partes do intervalo unitário para si mesmo, que têm inclinações de potência de 2 e pontos de quebra racionais diádicos, forma um grupo sob a operação de composição de funções . Este é o grupo de Thompson , o primeiro exemplo conhecido de um grupo simples infinito, mas finitamente apresentado . O mesmo grupo também pode ser representado por uma ação em árvores binárias enraizadas ou por uma ação nos racionais diádicos dentro do intervalo de unidade.

Outras construções relacionadas

Na matemática reversa , uma maneira de construir os números reais é representá-los como funções de números unários a racionais diádicos, onde o valor de uma dessas funções para o argumento é um racional diádico com denominador que se aproxima do número real dado. Definir números reais desta forma permite que muitos dos resultados básicos da análise matemática sejam comprovados dentro de uma teoria restrita da aritmética de segunda ordem chamada "análise viável" (BTFA). ${\ displaystyle i}$${\ displaystyle 2 ^ {i}}$

Os números surreais são gerados por um princípio de construção iterativa que começa gerando todos os racionais diádicos finitos e, em seguida, continua criando novos e estranhos tipos de números infinitos, infinitesimais e outros. Esse sistema numérico é fundamental para a teoria dos jogos combinatórios , e os racionais diádicos surgem naturalmente nessa teoria como o conjunto de valores de certos jogos combinatórios.

Os números fusíveis são um subconjunto dos racionais diádicos, o fechamento do conjunto sob a operação , restrito aos pares com . Eles são bem ordenados , com tipo de pedido igual ao número do épsilon . Para cada inteiro, o menor número fusível maior do que a forma . A existência de for each não pode ser provada na aritmética de Peano e cresce tão rapidamente em função disso, pois (na notação de seta para cima de Knuth para números grandes) já é maior do que . ${\ displaystyle \ {0 \}}$${\ displaystyle x, y \ mapsto (x + y + 1) / 2}$${\ displaystyle x, y}$${\ displaystyle | xy | <1}$ ${\ displaystyle \ varepsilon _ {0}}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n + 1/2 ^ {k}}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle n = 3}$${\ displaystyle 2 \ uparrow ^ {9} 16}$

Referências