Soma do prefixo - Prefix sum

Em ciência da computação , o prefixo soma , soma cumulativa , varredura inclusiva ou simplesmente varredura de uma sequência de números x ₀ , x ₁ , x ₂ , ... é uma segunda sequência de números y ₀ , y ₁ , y ₂ ,. .. , as somas dos prefixos ( totais corridos ) da sequência de entrada:

y ₀ = x ₀

y ₁ = x ₀ + x ₁

y ₂ = x ₀ + x ₁ + x ₂

...

Por exemplo, as somas de prefixo dos números naturais são os números triangulares :

números de entrada	1	2	3	4	5	6	...
somas de prefixo	1	3	6	10	15	21	...

As somas de prefixo são triviais para calcular em modelos sequenciais de computação, usando a fórmula y _i = y _{i - 1} + x _i para calcular cada valor de saída na ordem da sequência. No entanto, apesar de sua facilidade de cálculo, as somas de prefixo são um primitivo útil em certos algoritmos, como classificação de contagem , e formam a base da função de varredura de ordem superior em linguagens de programação funcionais . As somas de prefixo também têm sido muito estudadas em algoritmos paralelos , tanto como um problema de teste a ser resolvido quanto como uma primitiva útil a ser usada como uma sub-rotina em outros algoritmos paralelos.

Abstratamente, uma soma de prefixo requer apenas um operador associativo binário ⊕ , tornando-o útil para muitas aplicações, desde o cálculo de decomposições de pares bem separados de pontos até o processamento de strings.

Matematicamente, a operação de tomar somas de prefixo pode ser generalizada de sequências finitas a infinitas; nesse contexto, uma soma de prefixo é conhecida como uma soma parcial de uma série . Soma de prefixo ou soma parcial forma operadores lineares nos espaços vetoriais de sequências finitas ou infinitas; seus inversos são operadores de diferenças finitas .

Digitalizar função de ordem superior

Em termos de programação funcional , a soma do prefixo pode ser generalizada para qualquer operação binária (não apenas a operação de adição ); a função de ordem superior resultante dessa generalização é chamada de varredura e está intimamente relacionada à operação de dobra . As operações de varredura e de dobra aplicam a operação binária dada à mesma sequência de valores, mas diferem porque a varredura retorna toda a sequência de resultados da operação binária, enquanto a dobra retorna apenas o resultado final. Por exemplo, a sequência de números fatoriais pode ser gerada por uma varredura dos números naturais usando multiplicação em vez de adição:

números de entrada	1	2	3	4	5	6	...
produtos de prefixo	1	2	6	24	120	720	...

Verificações inclusivas e exclusivas

Linguagem de programação e implementações de biblioteca de varredura podem ser inclusivas ou exclusivas . Uma varredura inclusiva inclui a entrada x _i ao calcular a saída y _i (ou seja, ) , enquanto uma varredura exclusiva não (ou seja, ). No último caso, as implementações deixam y ₀ indefinido ou aceitam um valor " x ₋₁ " separado com o qual a varredura será propagada. Qualquer tipo de varredura pode ser transformado no outro: uma varredura inclusiva pode ser transformada em uma varredura exclusiva deslocando a matriz produzida pela varredura para a direita por um elemento e inserindo o valor de identidade à esquerda da matriz. Por outro lado, uma varredura exclusiva pode ser transformada em uma varredura inclusiva, deslocando a matriz produzida pela varredura para a esquerda e inserindo a soma do último elemento da varredura e o último elemento da matriz de entrada à direita da matriz. ${\ displaystyle y_ {i} = \ bigoplus _ {j = 0} ^ {i} x_ {j}}$${\ displaystyle y_ {i} = \ bigoplus _ {j = 0} ^ {i-1} x_ {j}}$

A tabela a seguir lista exemplos das funções de varredura inclusivas e exclusivas fornecidas por algumas linguagens de programação e bibliotecas:

Linguagem / biblioteca	Varredura inclusiva	Varredura exclusiva
Haskell	scanl1	scanl
MPI	MPI_Scan	MPI_Exscan
C ++	std::inclusive_scan	std::exclusive_scan
Scala	scan
Ferrugem	scan

Algoritmos paralelos

Existem dois algoritmos principais para calcular uma soma de prefixo em paralelo. O primeiro oferece um período mais curto e mais paralelismo, mas não é eficiente no trabalho. O segundo é eficiente no trabalho, mas requer o dobro da extensão e oferece menos paralelismo. Eles são apresentados a seguir.

Algoritmo 1: período mais curto, mais paralelo

Representação do circuito de uma soma de prefixo paralelo de 16 entradas altamente paralela

Hillis e Steele apresentam o seguinte algoritmo de soma de prefixo paralelo:

para a fazer${\ displaystyle i \ get 0}$ ${\ displaystyle \ lceil \ log _ {2} n \ rceil -1}$

para a fazer em paralelo${\ displaystyle j \ gets 0}$ ${\ displaystyle n-1}$

se então${\ displaystyle j <2 ^ {i}}$

${\ displaystyle x_ {j} ^ {i + 1} \ obtém x_ {j} ^ {i}}$

outro

${\ displaystyle x_ {j} ^ {i + 1} \ obtém x_ {j} ^ {i} + x_ {j-2 ^ {i}} ^ {i}}$

Acima, a notação significa o valor do j- ésimo elemento da matriz x na etapa de tempo i . ${\ displaystyle x_ {j} ^ {i}}$

Com um único processador, esse algoritmo seria executado em tempo O ( n log n ) . No entanto, se a máquina tiver pelo menos n processadores para realizar o loop interno em paralelo, o algoritmo como um todo é executado no tempo O (log n ) , o número de iterações do loop externo.

Algoritmo 2: Trabalho eficiente

Representação do circuito de uma soma de prefixo paralelo de 16 entradas eficiente no trabalho

Uma soma de prefixo paralelo com eficiência de trabalho pode ser calculada pelas etapas a seguir.

1. Calcule as somas de pares consecutivos de itens em que o primeiro item do par tem um índice par: z ₀ = x ₀ + x ₁ , z ₁ = x ₂ + x ₃ , etc.
2. Calcule recursivamente a soma do prefixo w ₀ , w ₁ , w ₂ , ... da sequência z ₀ , z ₁ , z ₂ , ...
3. Expresse cada termo da sequência final y ₀ , y ₁ , y ₂ , ... como a soma de até dois termos dessas sequências intermediárias: y ₀ = x ₀ , y ₁ = z ₀ , y ₂ = z ₀ + x ₂ , y ₃ = w ₀ , etc. Após o primeiro valor, cada número sucessivo y _i é copiado de uma posição na metade da seqüência w ou é o valor anterior adicionado a um valor na seqüência x .

Se a sequência de entrada tiver n passos, então a recursão continua até uma profundidade de O (log n ) , que também é o limite no tempo de execução paralelo desse algoritmo. O número de etapas do algoritmo é O ( n ) , e pode ser implementado em uma máquina de acesso aleatório paralela com O ( n / log n ) processadores sem qualquer desaceleração assintótica, atribuindo vários índices a cada processador em rodadas do algoritmo para que há mais elementos do que processadores.

Discussão

Cada um dos algoritmos anteriores é executado em tempo O (log n ) . No entanto, o primeiro leva exatamente log ₂ n passos, enquanto o último requer 2 log ₂  n - 2 passos. Para os exemplos de 16 entradas ilustrados, o Algoritmo 1 é paralelo de 12 vias (49 unidades de trabalho divididas por um intervalo de 4), enquanto o Algoritmo 2 é apenas paralelo de 4 vias (26 unidades de trabalho dividido por um intervalo de 6). No entanto, o Algoritmo 2 é eficiente no trabalho - ele executa apenas um fator constante (2) da quantidade de trabalho exigida pelo algoritmo sequencial - enquanto o Algoritmo 1 é ineficiente no trabalho - ele executa assintoticamente mais trabalho (um fator logarítmico) do que o necessário sequencialmente. Consequentemente, o Algoritmo 1 provavelmente terá um desempenho melhor quando o paralelismo abundante estiver disponível, mas o Algoritmo 2 provavelmente terá um desempenho melhor quando o paralelismo for mais limitado.

Os algoritmos paralelos para somas de prefixo podem frequentemente ser generalizados para outras operações de varredura em operações binárias associativas e também podem ser calculados de forma eficiente em hardware paralelo moderno, como uma GPU . A ideia de construir em hardware uma unidade funcional dedicada à computação de soma de prefixo multiparâmetro foi patenteada por Uzi Vishkin .

Muitas implementações paralelas seguem um procedimento de duas passagens, onde somas parciais de prefixo são calculadas na primeira passagem em cada unidade de processamento; a soma do prefixo dessas somas parciais é então calculada e transmitida de volta às unidades de processamento para uma segunda passagem usando o prefixo agora conhecido como o valor inicial. Assintoticamente, esse método leva aproximadamente duas operações de leitura e uma operação de gravação por item.

Implementações concretas de algoritmos de soma de prefixo

Uma implementação de um algoritmo de soma de prefixo paralelo, como outros algoritmos paralelos, deve levar em consideração a arquitetura de paralelização da plataforma. Mais especificamente, existem vários algoritmos que são adaptados para plataformas que trabalham em memória compartilhada , bem como algoritmos que são adequados para plataformas que usam memória distribuída , contando com a passagem de mensagens como a única forma de comunicação entre processos.

Memória compartilhada: algoritmo de dois níveis

O algoritmo a seguir assume um modelo de máquina de memória compartilhada ; todos os elementos de processamento (PEs) têm acesso à mesma memória. Uma versão desse algoritmo é implementada na Biblioteca de Modelos Padrão Multi-Core (MCSTL), uma implementação paralela da biblioteca de modelos padrão C ++ que fornece versões adaptadas para computação paralela de vários algoritmos.

Para calcular simultaneamente a soma do prefixo sobre os elementos de dados com elementos de processamento, os dados são divididos em blocos, cada um contendo elementos (para simplificar, assumimos que se divide ). Observe que, embora o algoritmo divida os dados em blocos, apenas os elementos de processamento são executados em paralelo por vez. ${\ displaystyle n}$${\ displaystyle p}$${\ displaystyle p + 1}$${\ displaystyle {\ frac {n} {p + 1}}}$${\ displaystyle p + 1}$${\ displaystyle n}$${\ displaystyle p + 1}$${\ displaystyle p}$

Em uma primeira varredura, cada PE calcula uma soma de prefixo local para seu bloco. O último bloco não precisa ser calculado, uma vez que essas somas de prefixo são calculadas apenas como compensações para as somas de prefixo dos blocos seguintes e o último bloco, por definição, não foi bem-sucedido.

Os deslocamentos que são armazenados na última posição de cada bloco são acumulados em uma soma de prefixo própria e armazenados em suas posições sucessivas. Por ser um número pequeno, é mais rápido fazer isso sequencialmente; para um grande , essa etapa também poderia ser feita em paralelo. ${\ displaystyle p}$${\ displaystyle p}$${\ displaystyle p}$

Uma segunda varredura é realizada. Desta vez, o primeiro bloco não precisa ser processado, pois não precisa levar em conta o deslocamento de um bloco anterior. No entanto, nesta varredura, o último bloco é incluído e as somas de prefixo para cada bloco são calculadas levando em consideração os deslocamentos de bloco de soma de prefixo calculados na varredura anterior.

function prefix_sum(elements) {
    n := size(elements)
    p := number of processing elements
    prefix_sum := [0...0] of size n
    
    do parallel i = 0 to p-1 {
        // i := index of current PE
        from j = i * n / (p+1) to (i+1) * n / (p+1) - 1 do {
            // This only stores the prefix sum of the local blocks
            store_prefix_sum_with_offset_in(elements, 0, prefix_sum)
        }
    }
    
    x = 0
    
    for i = 1 to p {                        // Serial accumulation of total sum of blocks 
        x +=  prefix_sum[i * n / (p+1) - 1] // Build the prefix sum over the first p blocks
        prefix_sum[i * n / (p+1)] = x       // Save the results to be used as offsets in second sweep
    }
    
    do parallel i = 1 to p {
        // i := index of current PE
        from j = i * n / (p+1) to (i+1) * n / (p+1) - 1 do {
            offset := prefix_sum[i * n / (p+1)]
            // Calculate the prefix sum taking the sum of preceding blocks as offset
            store_prefix_sum_with_offset_in(elements, offset, prefix_sum)
        }
    }
    
    return prefix_sum
}

Melhoria: Caso o número de blocos seja muito grande, o que torna a etapa serial demorada com a implantação de um único processador, o algoritmo de Hillis e Steele pode ser usado para acelerar a segunda fase.

Memória distribuída: algoritmo hipercubo

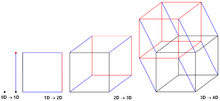
O Hypercube Prefix Sum Algorithm é bem adaptado para plataformas de memória distribuída e trabalha com a troca de mensagens entre os elementos de processamento. Ele assume que os elementos do processador (PEs) participam do algoritmo igual ao número de cantos em um hipercubo dimensional . ${\ displaystyle p = 2 ^ {d}}$${\ displaystyle d}$

Diferentes hipercubos para vários números de nós

Ao longo do algoritmo, cada PE é visto como um canto em um hipercubo hipotético com conhecimento da soma total do prefixo , bem como a soma do prefixo de todos os elementos até ele mesmo (de acordo com os índices ordenados entre os PEs), ambos em seu próprio hipercubo. ${\ displaystyle \ sigma}$${\ displaystyle x}$

• O algoritmo começa por assumir cada PE é o canto único de um cubo hiper dimensional zero e, portanto, e são iguais à soma prefixo local de seus próprios elementos.${\ displaystyle \ sigma}$${\ displaystyle x}$
• O algoritmo continua unificando hipercubos que são adjacentes ao longo de uma dimensão. Durante cada unificação, é trocado e agregado entre os dois hipercubos que mantém o invariante de que todos os PEs nos cantos deste novo hipercubo armazenam a soma total do prefixo deste hipercubo unificado recentemente em sua variável . Porém, apenas o hipercubo contendo os PEs com índice maior também adiciona isso à sua variável local , mantendo a invariante que armazena apenas o valor da soma do prefixo de todos os elementos nos PEs com índices menores ou iguais ao seu próprio índice.${\ displaystyle \ sigma}$${\ displaystyle \ sigma}$${\ displaystyle \ sigma}$${\ displaystyle x}$${\ displaystyle x}$

Em um hipercubo a-dimensional com PEs nos cantos, o algoritmo deve ser repetido vezes para que os hipercubos de dimensão zero sejam unificados em um hipercubo unidimensional . Assumindo um modelo de comunicação duplex onde o de dois PEs adjacentes em diferentes hipercubos podem ser trocados em ambas as direções em uma etapa de comunicação, isso significa o início da comunicação. ${\ displaystyle d}$${\ displaystyle 2 ^ {d}}$${\ displaystyle d}$${\ displaystyle 2 ^ {d}}$${\ displaystyle d}$${\ displaystyle \ sigma}$${\ displaystyle d = \ log _ {2} p}$

i := Index of own processor element (PE)
m := prefix sum of local elements of this PE
d := number of dimensions of the hyper cube

x = m;     // Invariant: The prefix sum up to this PE in the current sub cube
σ = m;     // Invariant: The prefix sum of all elements in the current sub cube

for (k=0; k <= d-1; k++) {
    y = σ @ PE(i xor 2^k)  // Get the total prefix sum of the opposing sub cube along dimension k
    σ = σ + y              // Aggregate the prefix sum of both sub cubes

    if (i & 2^k) {
        x = x + y  // Only aggregate the prefix sum from the other sub cube, if this PE is the higher index one.
    }
}

Tamanhos grandes de mensagens: árvore binária pipeline

O algoritmo Pipelined Binary Tree Algorithm é outro algoritmo para plataformas de memória distribuída que é especialmente adequado para grandes tamanhos de mensagens.

Como o algoritmo do hipercubo, ele assume uma estrutura de comunicação especial. Os elementos de processamento (PEs) são hipoteticamente arranjados em uma árvore binária (por exemplo, uma árvore de Fibonacci) com numeração de infixo de acordo com seu índice dentro dos PEs. A comunicação em tal árvore sempre ocorre entre os nós pai e filho.

A numeração infixa garante que para qualquer PE _j dado , os índices de todos os nós alcançáveis ​​por sua subárvore esquerda são menores que e os índices de todos os nós na subárvore direita são maiores que . Índice do pai é maior do que qualquer um dos índices em PE _j 's sub se PE _j é um filho esquerdo e menor se PE _j é uma criança direita. Isso permite o seguinte raciocínio: ${\ displaystyle \ mathbb {[l ... j-1]}}$${\ displaystyle j}$${\ displaystyle \ mathbb {[j + 1 ... r]}}$${\ displaystyle j}$

Troca de informações entre os elementos de processamento durante a fase ascendente (azul) e descendente (vermelha) no algoritmo Pipelined Binary Tree Prefix Sum.

• A soma do prefixo local da subárvore esquerda deve ser agregada para calcular a soma do prefixo local de PE _j .${\ displaystyle \ mathbb {\ oplus [l..j-1]}}$${\ displaystyle \ mathbb {\ oplus [l..j]}}$
• A soma do prefixo local da subárvore direita deve ser agregada para calcular a soma do prefixo local de PE _{h de} nível superior que são alcançados em um caminho que contém uma conexão de filhos à esquerda (o que significa ).${\ displaystyle \ mathbb {\ oplus [j + 1..r]}}$${\ displaystyle h> j}$
• A soma total do prefixo de PE _j é necessária para calcular as somas totais do prefixo na subárvore direita (por exemplo, para o nó de índice mais alto na subárvore).${\ displaystyle \ mathbb {\ oplus [0..j]}}$${\ displaystyle \ mathbb {\ oplus [0..j..r]}}$
• PE _j precisa incluir a soma total do prefixo do primeiro nó de ordem superior, que é alcançado por meio de um caminho ascendente, incluindo uma conexão de filhos certos para calcular sua soma total do prefixo.${\ displaystyle \ mathbb {\ oplus [0..l-1]}}$

Observe a distinção entre somas de prefixo local e subárvore total. Os pontos dois, três e quatro podem levar a crer que formariam uma dependência circular, mas não é o caso. PEs de nível inferior podem exigir a soma total do prefixo de PEs de nível superior para calcular sua soma de prefixo total, mas PEs de nível superior requerem apenas somas de prefixo local da subárvore para calcular sua soma de prefixo total. O nó raiz como o nó de nível mais alto requer apenas a soma do prefixo local de sua subárvore esquerda para calcular sua própria soma de prefixo. Cada PE no caminho de PE ₀ para a raiz PE requer apenas a soma do prefixo local de sua subárvore esquerda para calcular sua própria soma de prefixo, enquanto cada nó no caminho de PE _p-1 (último PE) para a _raiz PE requer o soma de prefixo total de seu pai para calcular sua própria soma de prefixo total.

Isso leva a um algoritmo de duas fases:

Fase ascendente
Propaga a soma do prefixo local da subárvore para seu pai para cada PE _j . ${\ displaystyle \ mathbb {\ oplus [l..j..r]}}$

Fase descendente
Propagar a soma total do prefixo exclusivo (PE _j exclusivo , bem como os PEs em sua subárvore esquerda) de todos os PEs de índice inferior que não estão incluídos na subárvore endereçada de PE _j para PEs de nível inferior na subárvore filha esquerda de PE _j . Propagar a soma do prefixo inclusivo para a subárvore filha certa de PE _j . ${\ displaystyle \ mathbb {\ oplus [0..l-1]}}$${\ displaystyle \ mathbb {\ oplus [0..j]}}$

Observe que o algoritmo é executado em paralelo em cada PE e os PEs serão bloqueados ao receberem até que seus filhos / pais lhes forneçam os pacotes.

k := number of packets in a message m of a PE
m @ {left, right, parent, this} := // Messages at the different PEs

x = m @ this

// Upward phase - Calculate subtree local prefix sums
for j=0 to k-1: // Pipelining: For each packet of a message
    if hasLeftChild:
        blocking receive m[j] @ left // This replaces the local m[j] with the received m[j]
        // Aggregate inclusive local prefix sum from lower index PEs
        x[j] = m[j] ⨁ x[j]

    if hasRightChild:
        blocking receive m[j] @ right
        // We do not aggregate m[j] into the local prefix sum, since the right children are higher index PEs
        send x[j] ⨁ m[j] to parent
    else:
        send x[j] to parent

// Downward phase
for j=0 to k-1:
    m[j] @ this = 0

    if hasParent:
        blocking receive m[j] @ parent
        // For a left child m[j] is the parents exclusive prefix sum, for a right child the inclusive prefix sum
        x[j] = m[j] ⨁ x[j] 
    
    send m[j] to left  // The total prefix sum of all PE's smaller than this or any PE in the left subtree
    send x[j] to right // The total prefix sum of all PE's smaller or equal than this PE

Pipelining

Se a mensagem de comprimento pode ser dividida em pacotes e o operador ⨁ pode ser usado em cada um dos pacotes de mensagem correspondentes separadamente, o pipelining é possível. ${\ displaystyle m}$${\ displaystyle n}$${\ displaystyle k}$

Se o algoritmo for usado sem pipelining, sempre haverá apenas dois níveis (os PEs de envio e os PEs de recebimento) da árvore binária em funcionamento enquanto todos os outros PEs estão esperando. Se houver elementos de processamento e uma árvore binária balanceada for usada, a árvore tem níveis, o comprimento do caminho de a é, portanto, o que representa o número máximo de operações de comunicação não paralelas durante a fase ascendente, da mesma forma, a comunicação no caminho descendente também é limitado a startups. Supondo que um tempo de inicialização de comunicação e um tempo de transmissão bytewise , as fases ascendente e descendente são limitadas a um cenário sem pipeline. ${\ displaystyle p}$${\ displaystyle \ log _ {2} p}$${\ displaystyle PE_ {0}}$${\ displaystyle PE _ {\ mathbb {root}}}$${\ displaystyle \ log _ {2} p-1}$${\ displaystyle \ log _ {2} p-1}$${\ displaystyle T _ {\ mathbb {start}}}$${\ displaystyle T _ {\ mathbb {byte}}}$${\ displaystyle (2 \ log _ {2} p-2) (T _ {\ mathbb {start}} + n * T _ {\ mathbb {byte}})}$

Após a divisão em k pacotes, cada um de tamanho e enviando-os separadamente, o primeiro pacote ainda precisa ser propagado como parte de uma soma de prefixo local e isso ocorrerá novamente para o último pacote se . No entanto, no meio, todos os PEs ao longo do caminho podem funcionar em paralelo e cada terceira operação de comunicação (receber à esquerda, receber à direita, enviar aos pais) envia um pacote para o próximo nível, de modo que uma fase possa ser concluída nas operações de comunicação e ambas as fases juntas precisam o que é favorável para tamanhos de mensagens grandes . ${\ displaystyle {\ frac {n} {k}}}$${\ displaystyle (\ log _ {2} p-1) (T _ {\ mathbb {start}} + {\ frac {n} {k}} * T _ {\ mathbb {byte}})}$${\ displaystyle PE _ {\ mathbb {root}}}$${\ displaystyle k> \ log _ {2} p}$${\ displaystyle 2 \ log _ {2} p-1 + 3 (k-1)}$${\ displaystyle (4 * \ log _ {2} p-2 + 6 (k-1)) (T _ {\ mathbb {start}} + {\ frac {n} {k}} * T _ {\ mathbb {byte }})}$${\ displaystyle n}$

O algoritmo pode ainda ser otimizado fazendo uso de full-duplex ou comunicação de modelo de telefone e sobrepondo a fase ascendente e a fase descendente.

Estruturas de dados

Quando um conjunto de dados pode ser atualizado dinamicamente, ele pode ser armazenado em uma estrutura de dados em árvore Fenwick . Essa estrutura permite a pesquisa de qualquer valor de soma de prefixo individual e a modificação de qualquer valor de matriz em tempo logarítmico por operação. No entanto, um artigo anterior de 1982 apresenta uma estrutura de dados chamada Partial Sums Tree (consulte a Seção 5.1) que parece se sobrepor às árvores Fenwick; em 1982, o termo soma de prefixo ainda não era tão comum quanto é hoje.

Para matrizes de dimensões mais altas, a tabela de área somada fornece uma estrutura de dados baseada em somas de prefixo para calcular somas de submatrizes retangulares arbitrárias. Isso pode ser um elemento primitivo útil nas operações de convolução de imagens .

Formulários

A classificação por contagem é um algoritmo de classificação de número inteiro que usa a soma do prefixo de um histograma de frequências de chave para calcular a posição de cada chave na matriz de saída classificada. Ele é executado em tempo linear para chaves inteiras que são menores do que o número de itens e é freqüentemente usado como parte da classificação radix , um algoritmo rápido para classificar inteiros que são menos restritos em magnitude.

A classificação de lista , o problema de transformar uma lista encadeada em uma matriz que representa a mesma sequência de itens, pode ser vista como computando uma soma de prefixo na sequência 1, 1, 1, ... e, em seguida, mapeando cada item para a posição da matriz dado por seu valor de soma de prefixo; combinando classificação de lista, somas de prefixo e passeios de Euler , muitos problemas importantes em árvores podem ser resolvidos por algoritmos paralelos eficientes.

Uma aplicação inicial de algoritmos de soma de prefixo paralelo foi no projeto de somadores binários , circuitos booleanos que podem adicionar dois números binários de n bits. Nesta aplicação, a sequência de bits de transporte da adição pode ser representada como uma operação de varredura na sequência de pares de bits de entrada, usando a função majoritária para combinar o transporte anterior com esses dois bits. Cada bit do número de saída pode então ser encontrado como o exclusivo ou de dois bits de entrada com o bit de transporte correspondente. Ao usar um circuito que executa as operações do algoritmo de soma de prefixo paralelo, é possível projetar um somador que usa O ( n ) portas lógicas e O (log n ) etapas de tempo.

No modelo de computação de máquina de acesso aleatório paralelo , somas de prefixo podem ser usadas para simular algoritmos paralelos que assumem a capacidade de vários processadores acessarem a mesma célula de memória ao mesmo tempo, em máquinas paralelas que proíbem o acesso simultâneo. Por meio de uma rede de classificação , um conjunto de solicitações de acesso à memória paralela pode ser ordenado em uma sequência de modo que os acessos à mesma célula sejam contíguos dentro da sequência; As operações de varredura podem então ser usadas para determinar qual dos acessos foi bem-sucedido na gravação em suas células solicitadas e para distribuir os resultados das operações de leitura de memória para vários processadores que solicitam o mesmo resultado.

Em Guy Blelloch 's Ph.D. Em tese, as operações de prefixo paralelas fazem parte da formalização do modelo de paralelismo de dados fornecido por máquinas como a Máquina de Conexão . A Máquina de Conexão CM-1 e CM-2 forneceu uma rede hipercúbica na qual o Algoritmo 1 acima poderia ser implementado, enquanto o CM-5 forneceu uma rede dedicada para implementar o Algoritmo 2.

Na construção de códigos Gray , sequências de valores binários com a propriedade de que valores de sequência consecutivos diferem uns dos outros em uma única posição de bit, um número n pode ser convertido no valor de código Gray na posição n da sequência simplesmente tomando o exclusivo ou de n e n / 2 (o número formado pelo deslocamento de n para a direita por uma única posição de bit). A operação reversa, decodificando um valor x codificado por Gray em um número binário, é mais complicada, mas pode ser expressa como a soma do prefixo dos bits de  x , onde cada operação de soma dentro da soma do prefixo é realizada módulo dois. Uma soma de prefixo deste tipo pode ser realizada de forma eficiente usando as operações booleanas bit a bit disponíveis em computadores modernos, calculando o exclusivo ou de x com cada um dos números formados deslocando x para a esquerda por um número de bits que é uma potência de dois .

O prefixo paralelo (usando multiplicação como a operação associativa subjacente) também pode ser usado para construir algoritmos rápidos para interpolação polinomial paralela . Em particular, pode ser usado para calcular os coeficientes de diferença divididos da forma de Newton do polinômio de interpolação. Esta abordagem baseada em prefixo também pode ser usada para obter as diferenças generalizadas divididas para interpolação Hermite (confluente) , bem como para algoritmos paralelos para sistemas Vandermonde .

Veja também

• Computação de uso geral em unidades de processamento gráfico
• Tabela de área somada

Referências

links externos

• Weisstein, Eric W. "Soma Cumulativa" . MathWorld .