Jet bundle - Jet bundle

Na topologia diferencial , o feixe de jato é uma determinada construção que faz um novo feixe de fibra lisa a partir de um determinado feixe de fibra lisa. Torna possível escrever equações diferenciais em seções de um feixe de fibras em uma forma invariável. Os jatos também podem ser vistos como versões livres de coordenadas das expansões de Taylor .

Historicamente, os feixes de jato são atribuídos a Charles Ehresmann , e foram um avanço no método ( prolongamento ) de Élie Cartan , de lidar geometricamente com derivadas mais altas , impondo condições de forma diferencial em variáveis ​​formais recém-introduzidas. Os feixes de jato às vezes são chamados de sprays , embora os sprays geralmente se refiram mais especificamente ao campo vetorial associado induzido no feixe correspondente (por exemplo, o spray geodésico nos manifolds Finsler ).

Desde o início dos anos 1980, os feixes de jato surgiram como uma forma concisa de descrever fenômenos associados às derivadas de mapas, particularmente aqueles associados ao cálculo de variações . Consequentemente, o jet bundle é agora reconhecido como o domínio correto para uma teoria de campo covariante geométrica e muito trabalho é feito em formulações relativísticas gerais de campos usando esta abordagem.

Jatos

Suponha que M seja uma variedade m- dimensional e que ( E , π, M ) seja um feixe de fibras . Para p ∈ M , seja Γ (p) o conjunto de todas as seções locais cujo domínio contém p . Deixe ser um índice múltiplo (uma m- dupla de números inteiros, não necessariamente em ordem crescente) e, em seguida, defina: ${\ displaystyle I = (I (1), I (2), ..., I (m))}$

${\ displaystyle {\ begin {alinhados} | I | &: = \ sum _ {i = 1} ^ {m} I (i) \\ {\ frac {\ partial ^ {| I |}} {\ partial x ^ {I}}} &: = \ prod _ {i = 1} ^ {m} \ left ({\ frac {\ partial} {\ partial x ^ {i}}} \ right) ^ {I (i) }. \ end {alinhado}}}$

Defina as seções locais σ, η ∈ Γ (p) para ter o mesmo r -jet em p se

${\ displaystyle \ left. {\ frac {\ partial ^ {| I |} \ sigma ^ {\ alpha}} {\ partial x ^ {I}}} \ right | _ {p} = \ left. {\ frac {\ partial ^ {| I |} \ eta ^ {\ alpha}} {\ partial x ^ {I}}} \ right | _ {p}, \ quad 0 \ leq | I | \ leq r.}$

A relação que dois mapas têm o mesmo r -jet é uma relação de equivalência . Um r -jet é uma classe de equivalência sob esta relação, e o r -jet com σ representativo é denotado . O inteiro r também é chamado de ordem do jato, p é sua origem e σ ( p ) é seu destino . ${\ displaystyle j_ {p} ^ {r} \ sigma}$

Manifolds de jato

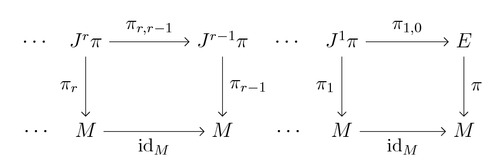
O r- ésimo coletor de jato de π é o conjunto

${\ displaystyle J ^ {r} (\ pi) = \ left \ {j_ {p} ^ {r} \ sigma: p \ in M, \ sigma \ in \ Gamma (p) \ right \}.}$

Podemos definir as projeções π _r e π _{r , 0} chamadas de projeções de origem e destino, respectivamente, por

${\ displaystyle {\ begin {cases} \ pi _ {r}: J ^ {r} (\ pi) \ to M \\ j_ {p} ^ {r} \ sigma \ mapsto p \ end {cases}}, \ qquad {\ begin {cases} \ pi _ {r, 0}: J ^ {r} (\ pi) \ to E \\ j_ {p} ^ {r} \ sigma \ mapsto \ sigma (p) \ end {casos}}}$

Se 1 ≤ k ≤ r , então a projeção k -jet é a função π _{r, k} definida por

${\ displaystyle {\ begin {cases} \ pi _ {r, k}: J ^ {r} (\ pi) \ to J ^ {k} (\ pi) \\ j_ {p} ^ {r} \ sigma \ mapsto j_ {p} ^ {k} \ sigma \ end {cases}}}$

Desta definição, fica claro que π _r = π o π _{r , 0} e que se 0 ≤ m ≤ k , então π _{r, m} = π _{k, m} o π _{r, k} . É convencional a considerar π _r, como o mapa de identidade em J  ^r ( π ) e para identificar J  ⁰ ( π ) com E .

As funções π _{r, k} , π _{r , 0} e π _r são submersões suaves sobrejetivas .

Um sistema de coordenadas em E irá gerar um sistema de coordenadas em J  ^r ( π ). Seja ( U , u ) um gráfico de coordenadas adaptado em E , onde u = ( x ⁱ , u ^α ). O gráfico de coordenadas induzidas ( U ^r , u ^r ) em J  ^r ( π ) é definido por

${\ displaystyle {\ begin {alinhado} U ^ {r} & = \ left \ {j_ {p} ^ {r} \ sigma: p \ in M, \ sigma (p) \ in U \ right \} \\ u ^ {r} & = \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) \ end {alinhado}}}$

Onde

${\ displaystyle {\ begin {alinhado} x ^ {i} \ left (j_ {p} ^ {r} \ sigma \ right) & = x ^ {i} (p) \\ u ^ {\ alpha} \ left (j_ {p} ^ {r} \ sigma \ right) & = u ^ {\ alpha} (\ sigma (p)) \ end {alinhado}}}$

e as funções conhecidas como coordenadas derivadas : ${\ displaystyle n \ left ({\ binom {m + r} {r}} - 1 \ right)}$

${\ displaystyle {\ begin {cases} u_ {I} ^ {\ alpha}: U ^ {k} \ to \ mathbf {R} \\ u_ {I} ^ {\ alpha} \ left (j_ {p} ^ {r} \ sigma \ direita) = \ esquerda. {\ frac {\ parcial ^ {| I |} \ sigma ^ {\ alpha}} {\ parcial x ^ {I}}} \ direita | _ {p} \ fim {casos}}}$

Dado um atlas de cartas adaptadas ( U , u ) em E , a coleção correspondente de cartas ( U  ^r , u  ^r ) é um C ^∞ atlas de dimensão finita em J  ^r ( π ).

Pacotes de jato

Uma vez que o atlas em cada define um colector, os triplos , e todos definir colectores fibrosos. Em particular, se for um feixe de fibras, o triplo define o r- ésimo feixe de jato de π . ${\ displaystyle J ^ {r} (\ pi)}$${\ displaystyle (J ^ {r} (\ pi), \ pi _ {r, k}, J ^ {k} (\ pi))}$${\ displaystyle (J ^ {r} (\ pi), \ pi _ {r, 0}, E)}$${\ displaystyle (J ^ {r} (\ pi), \ pi _ {r}, M)}$${\ displaystyle (E, \ pi, M)}$${\ displaystyle (J ^ {r} (\ pi), \ pi _ {r}, M)}$

Se W ⊂ M é uma subvariedade aberta, então

${\ displaystyle J ^ {r} \ left (\ pi | _ {\ pi ^ {- 1} (W)} \ right) \ cong \ pi _ {r} ^ {- 1} (W). \,}$

Se p ∈ M , então a fibra é denotada . ${\ displaystyle \ pi _ {r} ^ {- 1} (p) \,}$${\ displaystyle J_ {p} ^ {r} (\ pi)}$

Deixe σ ser uma secção local de π com domínio W ⊂ M . O r- ésimo prolongamento do jato de σ é o mapa definido por ${\ displaystyle j ^ {r} \ sigma: W \ rightarrow J ^ {r} (\ pi)}$

${\ displaystyle (j ^ {r} \ sigma) (p) = j_ {p} ^ {r} \ sigma. \,}$

Observe que , na verdade, é uma seção. Em coordenadas locais, é dado por ${\ displaystyle \ pi _ {r} \ circ j ^ {r} \ sigma = \ mathbb {id} _ {W}}$${\ displaystyle j ^ {r} \ sigma}$${\ displaystyle j ^ {r} \ sigma}$

${\ displaystyle \ left (\ sigma ^ {\ alpha}, {\ frac {\ partial ^ {| I |} \ sigma ^ {\ alpha}} {\ partial x ^ {I}}} \ right) \ qquad 1 \ leq | I | \ leq r. \,}$

Nós nos identificamos com . ${\ displaystyle j ^ {0} \ sigma}$${\ displaystyle \ sigma}$

Perspectiva algébrica-geométrica

É fornecida uma construção motivada de forma independente do feixe de seções .${\ displaystyle \ Gamma J ^ {k} \ left (\ pi _ {TM} \ right)}$

Considere um mapa diagonal , onde a variedade lisa é um espaço anelado localmente por para cada abertura . Que seja o feixe ideal de , equivalentemente seja o feixe de germes lisos que desaparecem para todos . A retirada do maço quociente a partir de pelo é o maço de k-jactos. ${\ textstyle \ Delta _ {n}: M \ to \ prod _ {i = 1} ^ {n + 1} M}$${\ displaystyle M}$${\ displaystyle C ^ {k} (U)}$${\ displaystyle U}$${\ displaystyle {\ mathcal {I}}}$${\ displaystyle \ Delta _ {n} (M)}$${\ displaystyle {\ mathcal {I}}}$${\ displaystyle \ Delta _ {n} (M)}$${\ displaystyle 0 <n \ leq k}$ ${\ displaystyle {\ Delta _ {n}} ^ {*} \ left ({\ mathcal {I}} / {\ mathcal {I}} ^ {n + 1} \ right)}$${\ textstyle \ prod _ {i = 1} ^ {n + 1} M}$${\ displaystyle M}$${\ displaystyle \ Delta _ {n}}$

O limite direto da sequência de injeções dada pelas inclusões canônicas de feixes, dá origem ao feixe de jato infinito . Observe que pela construção do limite direto é um anel filtrado. ${\ displaystyle {\ mathcal {I}} ^ {n + 1} \ hookrightarrow {\ mathcal {I}} ^ {n}}$ ${\ displaystyle {\ mathcal {J}} ^ {\ infty} (TM)}$

Exemplo

Se π é o feixe trivial ( M × R , RP ₁ , H ), então existe uma canónica difeomorfismo entre o primeiro conjunto de jacto e o t * M × R . Para construir este difeomorfismo, para cada σ na escrita . ${\ displaystyle J ^ {1} (\ pi)}$${\ displaystyle \ Gamma _ {M} (\ pi)}$${\ displaystyle {\ bar {\ sigma}} = pr_ {2} \ circ \ sigma \ in C ^ {\ infty} (M) \,}$

Então, sempre que p ∈ M

${\ displaystyle j_ {p} ^ {1} \ sigma = \ left \ {\ psi: \ psi \ in \ Gamma _ {p} (\ pi); {\ bar {\ psi}} (p) = {\ bar {\ sigma}} (p); d {\ bar {\ psi}} _ {p} = d {\ bar {\ sigma}} _ {p} \ right \}. \,}$

Consequentemente, o mapeamento

${\ displaystyle {\ begin {cases} J ^ {1} (\ pi) \ to T ^ {*} M \ times \ mathbf {R} \\ j_ {p} ^ {1} \ sigma \ mapsto \ left ( d {\ bar {\ sigma}} _ {p}, {\ bar {\ sigma}} (p) \ right) \ end {cases}}}$

é bem definido e é claramente injetivo . Escrevê-lo em coordenadas mostra que é um difeomorfismo, porque se (x ⁱ , u) são coordenadas em M × R , onde u = id _R é a coordenada de identidade, então as coordenadas derivadas u _i em J ¹ (π) correspondem às coordenadas ∂ _i em T * M .

Da mesma forma, se π é o feixe trivial ( R × M , pr ₁ , R ), então existe um difeomorfismo canônico entre e R × TM . ${\ displaystyle J ^ {1} (\ pi)}$

Estrutura de contato

O espaço J ^r (π) carrega uma distribuição natural , ou seja, um sub-feixe do feixe tangente TJ ^r (π)), chamada de distribuição de Cartan . A distribuição Cartan é abrangida por todos os planos tangentes a gráficos de seções holonômicas; isto é, seções da forma j ^r φ para φ uma seção de π.

O aniquilador da distribuição Cartan é um espaço de formas únicas diferenciais chamadas formas de contato , em J ^r (π). O espaço das formas diferenciadas em J ^r (π) é denotado por e o espaço das formas de contato é denotado por . Um formulário é um formulário de contato, desde que seu recuo a cada prolongamento seja zero. Em outras palavras, é um formulário de contato se e somente se ${\ displaystyle \ Lambda ^ {1} J ^ {r} (\ pi)}$${\ displaystyle \ Lambda _ {C} ^ {r} \ pi}$${\ displaystyle \ theta \ in \ Lambda ^ {1} J ^ {r} \ pi}$

${\ displaystyle \ left (j ^ {r + 1} \ sigma \ right) ^ {*} \ theta = 0}$

para todas as secções locais σ de π sobre M .

A distribuição Cartan é a principal estrutura geométrica em espaços a jato e desempenha um papel importante na teoria geométrica de equações diferenciais parciais . As distribuições Cartan são totalmente não integráveis. Em particular, eles não são involutivos . A dimensão da distribuição Cartan cresce com a ordem do espaço do jato. No entanto, no espaço de jactos infinitas J ^∞ a distribuição Cartan torna-se Involutivas e finitos-dimensional: seus coincide com a dimensão de dimensão da base do colector de M .

Exemplo

Consideremos o caso de (E, π, M) , onde E ≃ R ² e M ≃ R . Então, (J ¹ (π), π, M) define o primeiro feixe de jato, e pode ser coordenado por (x, u, u ₁ ) , onde

${\ displaystyle {\ begin {alinhado} x \ left (j_ {p} ^ {1} \ sigma \ right) & = x (p) = x \\ u \ left (j_ {p} ^ {1} \ sigma \ right) & = u (\ sigma (p)) = u (\ sigma (x)) = \ sigma (x) \\ u_ {1} \ left (j_ {p} ^ {1} \ sigma \ right) & = \ left. {\ frac {\ partial \ sigma} {\ partial x}} \ right | _ {p} = \ sigma '(x) \ end {alinhados}}}$

para todo p ∈ M e σ em Γ _p (π). Uma forma 1 geral em J ¹ (π) assume a forma

${\ displaystyle \ theta = a (x, u, u_ {1}) dx + b (x, u, u_ {1}) du + c (x, u, u_ {1}) du_ {1} \,}$

Uma seção σ em Γ _p (π) tem primeiro prolongamento

${\ displaystyle j ^ {1} \ sigma = (u, u_ {1}) = \ left (\ sigma (p), \ left. {\ frac {\ partial \ sigma} {\ partial x}} \ right | _ {p} \ direita).}$

Portanto, (j ¹ σ) * θ pode ser calculado como

${\ displaystyle {\ begin {alinhado} \ left (j_ {p} ^ {1} \ sigma \ right) ^ {*} \ theta & = \ theta \ circ j_ {p} ^ {1} \ sigma \\ & = a (x, \ sigma (x), \ sigma '(x)) dx + b (x, \ sigma (x), \ sigma' (x)) d (\ sigma (x)) + c (x, \ sigma (x), \ sigma '(x)) d (\ sigma' (x)) \\ & = a (x, \ sigma (x), \ sigma '(x)) dx + b (x, \ sigma (x), \ sigma '(x)) \ sigma' (x) dx + c (x, \ sigma (x), \ sigma '(x)) \ sigma' '(x) dx \\ & = [ a (x, \ sigma (x), \ sigma '(x)) + b (x, \ sigma (x), \ sigma' (x)) \ sigma '(x) + c (x, \ sigma (x ), \ sigma '(x)) \ sigma' '(x)] dx \ end {alinhado}}}$

Isso desaparecerá para todas as seções σ se e somente se c = 0 e a = - bσ ′ (x) . Portanto, θ = b (x, u, u ₁ ) θ ₀ deve ser necessariamente um múltiplo da forma de contato básica θ ₀ = du - u ₁ dx . Prosseguindo para o segundo espaço de jato J ² (π) com coordenada adicional u ₂ , de modo que

${\ displaystyle u_ {2} (j_ {p} ^ {2} \ sigma) = \ left. {\ frac {\ partial ^ {2} \ sigma} {\ partial x ^ {2}}} \ right | _ {p} = \ sigma '' (x) \,}$

um formulário 1 geral tem a construção

${\ displaystyle \ theta = a (x, u, u_ {1}, u_ {2}) dx + b (x, u, u_ {1}, u_ {2}) du + c (x, u, u_ { 1}, u_ {2}) du_ {1} + e (x, u, u_ {1}, u_ {2}) du_ {2} \,}$

Este é um formulário de contato se e somente se

${\ displaystyle {\ begin {alinhado} \ left (j_ {p} ^ {2} \ sigma \ right) ^ {*} \ theta & = \ theta \ circ j_ {p} ^ {2} \ sigma \\ & = a (x, \ sigma (x), \ sigma '(x), \ sigma' '(x)) dx + b (x, \ sigma (x), \ sigma' (x), \ sigma '' ( x)) d (\ sigma (x)) + {} \\ & \ qquad \ qquad c (x, \ sigma (x), \ sigma '(x), \ sigma' '(x)) d (\ sigma '(x)) + e (x, \ sigma (x), \ sigma' (x), \ sigma '' (x)) d (\ sigma '' (x)) \\ & = adx + b \ sigma '(x) dx + c \ sigma' '(x) dx + e \ sigma' '' (x) dx \\ & = [a + b \ sigma '(x) + c \ sigma' '(x) + e \ sigma '' '(x)] dx \\ & = 0 \ end {alinhado}}}$

o que implica que e = 0 e a = - bσ ′ (x) - cσ ′ ′ (x) . Portanto, θ é um formulário de contato se e somente se

${\ displaystyle \ theta = b (x, \ sigma (x), \ sigma '(x)) \ theta _ {0} + c (x, \ sigma (x), \ sigma' (x)) \ theta _ {1},}$

onde θ ₁ = du ₁ - u ₂ dx é a próxima forma de contato básica (Observe que aqui estamos identificando a forma θ ₀ com seu retrocesso para J ² (π) ). ${\ displaystyle \ left (\ pi _ {2,1} \ right) ^ {*} \ theta _ {0}}$

Em geral, fornecendo x, u ∈ R , um formulário de contato em J ^{r + 1} (π) pode ser escrito como uma combinação linear dos formulários de contato básicos

${\ displaystyle \ theta _ {k} = du_ {k} -u_ {k + 1} dx \ qquad k = 0, \ ldots, r-1 \,}$

Onde

${\ displaystyle u_ {k} \ left (j ^ {k} \ sigma \ right) = \ left. {\ frac {\ partial ^ {k} \ sigma} {\ partial x ^ {k}}} \ right | _ {p}.}$

Argumentos semelhantes levam a uma caracterização completa de todas as formas de contato.

Em coordenadas locais, cada formulário de contato em J ^{r + 1} (π) pode ser escrito como uma combinação linear

${\ displaystyle \ theta = \ sum _ {| I | = 0} ^ {r} P _ {\ alpha} ^ {I} \ theta _ {I} ^ {\ alpha}}$

com coeficientes suaves das formas básicas de contato ${\ displaystyle P_ {i} ^ {\ alpha} (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha})}$

${\ displaystyle \ theta _ {I} ^ {\ alpha} = du_ {I} ^ {\ alpha} -u_ {I, i} ^ {\ alpha} dx ^ {i} \,}$

| I | é conhecido como a ordem do formulário de contato . Observe que os formulários de contato em J ^{r + 1} (π) têm pedidos no máximo r . As formas de contato fornecem uma caracterização das seções locais de π _{r + 1} que são prolongamentos das seções de π. ${\ displaystyle \ theta _ {i} ^ {\ alpha}}$

Seja ψ ∈ Γ _W ( π _{r + 1} ), então ψ = j ^{r + 1} σ onde σ ∈ Γ _W (π) se e somente se${\ displaystyle \ psi ^ {*} (\ theta | _ {W}) = 0, \ forall \ theta \ in \ Lambda _ {C} ^ {1} \ pi _ {r + 1, r}. \, }$

Campos vetoriais

Um campo vetorial geral no espaço total E , coordenado por , é ${\ displaystyle (x, u) \ {\ stackrel {\ mathrm {def}} {=}} \ \ left (x ^ {i}, u ^ {\ alpha} \ right) \,}$

${\ displaystyle V \ {\ stackrel {\ mathrm {def}} {=}} \ \ rho ^ {i} (x, u) {\ frac {\ partial} {\ partial x ^ {i}}} + \ phi ^ {\ alpha} (x, u) {\ frac {\ partial} {\ partial u ^ {\ alpha}}}. \,}$

Um campo vetorial é denominado horizontal , o que significa que todos os coeficientes verticais desaparecem, se = 0. ${\ displaystyle \ phi ^ {\ alpha}}$

Um campo vetorial é denominado vertical , o que significa que todos os coeficientes horizontais desaparecem, se ρ ⁱ = 0.

Para fixo (x, u) , identificamos

${\ displaystyle V _ {(x, u)} \ {\ stackrel {\ mathrm {def}} {=}} \ \ rho ^ {i} (x, u) {\ frac {\ partial} {\ partial x ^ {i}}} + \ phi ^ {\ alpha} (x, u) {\ frac {\ partial} {\ partial u ^ {\ alpha}}} \,}$

tendo as coordenadas (x, u, ρ ⁱ , & Phi; ^ct ) , com um elemento em fibra t _xu E de TE sobre (x, u) em E , chamado um vector tangente em TE . Uma secção

${\ displaystyle {\ begin {cases} \ psi: E \ to TE \\ (x, u) \ mapsto \ psi (x, u) = V \ end {cases}}}$

é chamado de campo vetorial em E com

${\ displaystyle V = \ rho ^ {i} (x, u) {\ frac {\ partial} {\ partial x ^ {i}}} + \ phi ^ {\ alpha} (x, u) {\ frac { \ parcial} {\ parcial u ^ {\ alpha}}}}$

e ψ em Γ (TE) .

O pacote de jato J ^r (π) é coordenado por . Para fixo (x, u, w) , identifique ${\ displaystyle (x, u, w) \ {\ stackrel {\ mathrm {def}} {=}} \ (x ^ {i}, u ^ {\ alpha}, w_ {i} ^ {\ alpha}) \,}$

${\ displaystyle V _ {(x, u, w)} \ {\ stackrel {\ mathrm {def}} {=}} \ V ^ {i} (x, u, w) {\ frac {\ partial} {\ parcial x ^ {i}}} + V ^ {\ alpha} (x, u, w) {\ frac {\ parcial} {\ parcial u ^ {\ alpha}}} + V_ {i} ^ {\ alpha} (x, u, w) {\ frac {\ partial} {\ partial w_ {i} ^ {\ alpha}}} + V_ {i_ {1} i_ {2}} ^ {\ alpha} (x, u, w) {\ frac {\ partial} {\ partial w_ {i_ {1} i_ {2}} ^ {\ alpha}}} + \ cdots + V_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha} (x, u, w) {\ frac {\ partial} {\ partial w_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha}}}}$

tendo coordenadas

${\ displaystyle \ left (x, u, w, v_ {i} ^ {\ alpha}, v_ {i_ {1} i_ {2}} ^ {\ alpha}, \ cdots, v_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha} \ right),}$

com um elemento na fibra de TJ ^r (π) sobre (x, u, w) ∈ J ^r (π) , chamado de vetor tangente em TJ ^r (π) . Aqui, ${\ displaystyle T_ {xuw} (J ^ {r} \ pi)}$

${\ displaystyle v_ {i} ^ {\ alpha}, v_ {i_ {1} i_ {2}} ^ {\ alpha}, \ cdots, v_ {i_ {1} \ cdots i_ {r}} ^ {\ alpha }}$

são funções com valor real em J ^r (π) . Uma secção

${\ displaystyle {\ begin {cases} \ Psi: J ^ {r} (\ pi) \ to TJ ^ {r} (\ pi) \\ (x, u, w) \ mapsto \ Psi (u, w) = V \ final {casos}}}$

é um campo vetorial em J ^r (π) , e dizemos${\ displaystyle \ Psi \ in \ Gamma (T (J ^ {r} \ pi)).}$

Equações diferenciais parciais

Seja (E, π, M) um feixe de fibras. Uma equação diferencial parcial de ordem r em π é uma subvariedade S embutida fechada da variedade de jato J ^r (π) . Uma solução é uma secção local σ ∈ Γ _W (π) satisfazendo , para todos os p em M . ${\ displaystyle j_ {p} ^ {r} \ sigma \ in S}$

Considere um exemplo de uma equação diferencial parcial de primeira ordem.

Exemplo

Seja π o pacote trivial ( R ² × R , pr ₁ , R ² ) com coordenadas globais ( x ¹ , x ² , u ¹ ). Então o mapa F  : J ¹ (π) → R definido por

${\ displaystyle F = u_ {1} ^ {1} u_ {2} ^ {1} -2x ^ {2} u ^ {1}}$

dá origem à equação diferencial

${\ displaystyle S = \ left \ {j_ {p} ^ {1} \ sigma \ in J ^ {1} \ pi \: \ \ left (u_ {1} ^ {1} u_ {2} ^ {1} -2x ^ {2} u ^ {1} \ direita) \ esquerda (j_ {p} ^ {1} \ sigma \ direita) = 0 \ direita \}}$

que pode ser escrito

${\ displaystyle {\ frac {\ partial \ sigma} {\ partial x ^ {1}}} {\ frac {\ partial \ sigma} {\ partial x ^ {2}}} - 2x ^ {2} \ sigma = 0.}$

O particular

${\ displaystyle {\ begin {cases} \ sigma: \ mathbf {R} ^ {2} \ to \ mathbf {R} ^ {2} \ times \ mathbf {R} \\\ sigma (p_ {1}, p_ {2}) = \ left (p ^ {1}, p ^ {2}, p ^ {1} (p ^ {2}) ^ {2} \ right) \ end {casos}}}$

tem primeiro prolongamento dado por

${\ displaystyle j ^ {1} \ sigma \ left (p_ {1}, p_ {2} \ right) = \ left (p ^ {1}, p ^ {2}, p ^ {1} \ left (p ^ {2} \ right) ^ {2}, \ left (p ^ {2} \ right) ^ {2}, 2p ^ {1} p ^ {2} \ right)}$

e é uma solução desta equação diferencial, porque

${\ displaystyle {\ begin {alinhado} \ left (u_ {1} ^ {1} u_ {2} ^ {1} -2x ^ {2} u ^ {1} \ right) \ left (j_ {p} ^ {1} \ sigma \ direita) & = u_ {1} ^ {1} \ esquerda (j_ {p} ^ {1} \ sigma \ direita) u_ {2} ^ {1} \ esquerda (j_ {p} ^ {1} \ sigma \ right) -2x ^ {2} \ left (j_ {p} ^ {1} \ sigma \ right) u ^ {1} \ left (j_ {p} ^ {1} \ sigma \ right ) \\ & = \ left (p ^ {2} \ right) ^ {2} \ cdot 2p ^ {1} p ^ {2} -2 \ cdot p ^ {2} \ cdot p ^ {1} \ left (p ^ {2} \ right) ^ {2} \\ & = 2p ^ {1} \ left (p ^ {2} \ right) ^ {3} -2p ^ {1} \ left (p ^ {2 } \ right) ^ {3} \\ & = 0 \ end {alinhado}}}$

e assim para todo p ∈ R ² . ${\ displaystyle j_ {p} ^ {1} \ sigma \ in S}$

Prolongamento de jato

Um difeomorfismo local ψ  : J ^r ( π ) → J ^r ( π ) define uma transformação de contato de ordem r se preserva o contato ideal, o que significa que se θ é qualquer forma de contato em J ^r ( π ), então ψ * θ é também um formulário de contato.

O fluxo gerado por um campo vetorial V ^r no espaço do jato J ^r (π) forma um grupo de um parâmetro de transformações de contato se e somente se a derivada de Lie de qualquer forma de contato θ preserva o contato ideal. ${\ displaystyle {\ mathcal {L}} _ {V ^ {r}} (\ theta)}$

Vamos começar com o caso de primeira ordem. Considere um campo vetorial geral V ¹ em J ¹ ( π ), dado por

${\ displaystyle V ^ {1} \ {\ stackrel {\ mathrm {def}} {=}} \ \ rho ^ {i} \ left (x ^ {i} \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) {\ frac {\ partial} {\ partial x ^ {i}}} + \ phi ^ {\ alpha} \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) {\ frac {\ partial} {\ partial u ^ {\ alpha}}} + \ chi _ {i} ^ {\ alpha} \ left (x ^ {i}, u ^ {\ alpha}, u_ {I} ^ {\ alpha} \ right) {\ frac {\ partial} {\ partial u_ {i} ^ {\ alpha}}}.}$

Agora aplicamos as formas básicas de contato e expandimos a derivada externa das funções em termos de suas coordenadas para obter: ${\ displaystyle {\ mathcal {L}} _ {V ^ {1}}}$${\ displaystyle \ theta _ {0} ^ {\ alpha} = du ^ {\ alpha} -u_ {i} ^ {\ alpha} dx ^ {i},}$

${\ displaystyle {\ begin {align} {\ mathcal {L}} _ {V ^ {1}} \ left (\ theta _ {0} ^ {\ alpha} \ right) & = {\ mathcal {L}} _ {V ^ {1}} \ left (du ^ {\ alpha} -u_ {i} ^ {\ alpha} dx ^ {i} \ right) \\ & = {\ mathcal {L}} _ {V ^ {1}} du ^ {\ alpha} - \ left ({\ mathcal {L}} _ {V ^ {1}} u_ {i} ^ {\ alpha} \ right) dx ^ {i} -u_ {i } ^ {\ alpha} \ left ({\ mathcal {L}} _ {V ^ {1}} dx ^ {i} \ right) \\ & = d \ left (V ^ {1} u ^ {\ alpha } \ right) -V ^ {1} u_ {i} ^ {\ alpha} dx ^ {i} -u_ {i} ^ {\ alpha} d \ left (V ^ {1} x ^ {i} \ right ) \\ & = d \ phi ^ {\ alpha} - \ chi _ {i} ^ {\ alpha} dx ^ {i} -u_ {i} ^ {\ alpha} d \ rho ^ {i} \\ & = {\ frac {\ parcial \ phi ^ {\ alpha}} {\ parcial x ^ {i}}} dx ^ {i} + {\ frac {\ parcial \ phi ^ {\ alpha}} {\ parcial u ^ {k}}} du ^ {k} + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ {i} ^ {k}}} du_ {i} ^ {k} - \ chi _ {i} ^ {\ alpha} dx ^ {i} -u_ {i} ^ {\ alpha} \ left [{\ frac {\ partial \ rho ^ {i}} {\ partial x ^ {m}}} dx ^ {m} + {\ frac {\ parcial \ rho ^ {i}} {\ parcial u ^ {k}}} du ^ {k} + {\ frac {\ parcial \ rho ^ {i}} {\ parcial u_ {m} ^ {k}}} du_ {m} ^ {k} \ right] \\ & = {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial x ^ {i}}} dx ^ {i} + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u ^ {k}}} \ left (\ th eta ^ {k} + u_ {i} ^ {k} dx ^ {i} \ right) + {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ {i} ^ {k}}} du_ {i} ^ {k} - \ chi _ {i} ^ {\ alpha} dx ^ {i} -u_ {l} ^ {\ alpha} \ left [{\ frac {\ partial \ rho ^ {l} } {\ parcial x ^ {i}}} dx ^ {i} + {\ frac {\ parcial \ rho ^ {l}} {\ parcial u ^ {k}}} \ esquerdo (\ theta ^ {k} + u_ {i} ^ {k} dx ^ {i} \ right) + {\ frac {\ parcial \ rho ^ {l}} {\ parcial u_ {i} ^ {k}}} du_ {i} ^ {k } \ right] \\ & = \ left [{\ frac {\ partial \ phi ^ {\ alpha}} {\ partial x ^ {i}}} + {\ frac {\ partial \ phi ^ {\ alpha}} {\ parcial u ^ {k}}} u_ {i} ^ {k} -u_ {l} ^ {\ alpha} \ left ({\ frac {\ partial \ rho ^ {l}} {\ partial x ^ { i}}} + {\ frac {\ parcial \ rho ^ {l}} {\ parcial u ^ {k}}} u_ {i} ^ {k} \ direita) - \ chi _ {i} ^ {\ alpha } \ right] dx ^ {i} + \ left [{\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ {i} ^ {k}}} - u_ {l} ^ {\ alpha} {\ frac {\ partial \ rho ^ {l}} {\ partial u_ {i} ^ {k}}} \ right] du_ {i} ^ {k} + \ left ({\ frac {\ partial \ phi ^ {\ alpha}} {\ parcial u ^ {k}}} - u_ {l} ^ {\ alpha} {\ frac {\ parcial \ rho ^ {l}} {\ parcial u ^ {k}}} \ direita ) \ theta ^ {k} \ end {alinhado}}}$

Portanto, V ¹ determina uma transformação de contato se e somente se os coeficientes de dx ⁱ e na fórmula desaparecerem. Os últimos requisitos implicam nas condições de contato${\ displaystyle du_ {i} ^ {k}}$

${\ displaystyle {\ frac {\ partial \ phi ^ {\ alpha}} {\ partial u_ {i} ^ {k}}} - u_ {l} ^ {\ alpha} {\ frac {\ partial \ rho ^ { l}} {\ parcial u_ {i} ^ {k}}} = 0}$

Os primeiros requisitos fornecem fórmulas explícitas para os coeficientes dos primeiros termos derivados em V ¹ :

${\ displaystyle \ chi _ {i} ^ {\ alpha} = {\ widehat {D}} _ {i} \ phi ^ {\ alpha} -u_ {l} ^ {\ alpha} \ left ({\ widehat { D}} _ {i} \ rho ^ {l} \ right)}$

Onde

${\ displaystyle {\ widehat {D}} _ {i} = {\ frac {\ partial} {\ partial x ^ {i}}} + u_ {i} ^ {k} {\ frac {\ partial} {\ u parcial ^ {k}}}}$

denota o truncamento de ordem zero da derivada total D _i .

Assim, as condições de contato prescrevem exclusivamente o prolongamento de qualquer ponto ou campo vetorial de contato. Ou seja, se satisfizer essas equações, V ^r é chamado de r- ésimo prolongamento de V para um campo vetorial em J ^r (π) . ${\ displaystyle {\ mathcal {L}} _ {V ^ {r}}}$

Esses resultados são mais bem compreendidos quando aplicados a um exemplo particular. Portanto, vamos examinar o seguinte.

Exemplo

Consideremos o caso de (E, π, M) , onde E ≅ R ² e M ≃ R . Então, (J ¹ (π), π, E) define o primeiro feixe de jato, e pode ser coordenado por (x, u, u ₁ ) , onde

${\ displaystyle {\ begin {alinhados} x (j_ {p} ^ {1} \ sigma) & = x (p) = x \\ u (j_ {p} ^ {1} \ sigma) & = u (\ sigma (p)) = u (\ sigma (x)) = \ sigma (x) \\ u_ {1} (j_ {p} ^ {1} \ sigma) & = \ left. {\ frac {\ partial \ sigma} {\ parcial x}} \ direita | _ {p} = {\ ponto {\ sigma}} (x) \ end {alinhado}}}$

para todo p ∈ M e σ em Γ _p ( π ). Um formulário de contato em J ¹ (π) tem o formulário

${\ displaystyle \ theta = du-u_ {1} dx}$

Considere um vetor V em E , tendo a forma

${\ displaystyle V = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}}}$

Então, o primeiro prolongamento deste campo vetorial para J ¹ (π) é

${\ displaystyle {\ begin {alinhados} V ^ {1} & = V + Z \\ & = x {\ frac {\ parcial} {\ parcial u}} - u {\ frac {\ parcial} {\ parcial x }} + Z \\ & = x {\ frac {\ parcial} {\ parcial u}} - u {\ frac {\ parcial} {\ parcial x}} + \ rho (x, u, u_ {1}) {\ frac {\ partial} {\ partial u_ {1}}} \ end {alinhado}}}$

Se agora tomarmos a derivada de Lie da forma de contato em relação a este campo vetorial prolongado, obteremos ${\ displaystyle {\ mathcal {L}} _ {V ^ {1}} (\ theta),}$

${\ displaystyle {\ begin {align} {\ mathcal {L}} _ {V ^ {1}} (\ theta) & = {\ mathcal {L}} _ {V ^ {1}} (du-u_ { 1} dx) \\ & = {\ mathcal {L}} _ {V ^ {1}} du- \ left ({\ mathcal {L}} _ {V ^ {1}} u_ {1} \ right) dx-u_ {1} \ left ({\ mathcal {L}} _ {V ^ {1}} dx \ right) \\ & = d \ left (V ^ {1} u \ right) -V ^ {1 } u_ {1} dx-u_ {1} d \ left (V ^ {1} x \ right) \\ & = dx- \ rho (x, u, u_ {1}) dx + u_ {1} du \ \ & = (1- \ rho (x, u, u_ {1})) dx + u_ {1} du \\ & = [1- \ rho (x, u, u_ {1})] dx + u_ { 1} (\ theta + u_ {1} dx) && du = \ theta + u_ {1} dx \\ & = [1 + u_ {1} u_ {1} - \ rho (x, u, u_ {1}) ] dx + u_ {1} \ theta \ end {alinhado}}}$

Portanto, para preservação do ideal de contato, exigimos

${\ displaystyle 1 + u_ {1} u_ {1} - \ rho (x, u, u_ {1}) = 0 \ quad \ Leftrightarrow \ quad \ rho (x, u, u_ {1}) = 1 + u_ {1} u_ {1}.}$

E assim o primeiro prolongamento de V para um campo vetorial em J ¹ (π) é

${\ displaystyle V ^ {1} = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}} + (1 + u_ {1} u_ {1} ) {\ frac {\ parcial} {\ parcial u_ {1}}}.}$

Vamos calcular também o segundo prolongamento de V para um campo vetorial em J ² (π) . Temos como coordenadas em J ² (π) . Portanto, o vetor prolongado tem a forma ${\ displaystyle \ {x, u, u_ {1}, u_ {2} \}}$

${\ displaystyle V ^ {2} = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}} + \ rho (x, u, u_ {1} , u_ {2}) {\ frac {\ parcial} {\ parcial u_ {1}}} + \ phi (x, u, u_ {1}, u_ {2}) {\ frac {\ parcial} {\ parcial u_ {2}}}.}$

Os formulários de contato são

${\ displaystyle {\ begin {alinhado} \ theta & = du-u_ {1} dx \\\ theta _ {1} & = du_ {1} -u_ {2} dx \ end {alinhado}}}$

Para preservar o contato ideal, exigimos

${\ displaystyle {\ begin {align} {\ mathcal {L}} _ {V ^ {2}} (\ theta) = 0 \\ {\ mathcal {L}} _ {V ^ {2}} (\ theta _ {1}) = 0 \ fim {alinhado}}}$

Agora, θ não tem dependência de u ₂ . Conseqüentemente, dessa equação pegaremos a fórmula para ρ , que será necessariamente o mesmo resultado que encontramos para V ¹ . Portanto, o problema é análogo a prolongar o campo vetorial V ¹ para J ² (π). Ou seja, podemos gerar o r- ésimo prolongamento de um campo vetorial aplicando recursivamente a derivada de Lie das formas de contato em relação aos campos vetoriais prolongados, r vezes. Então nós temos

${\ displaystyle \ rho (x, u, u_ {1}) = 1 + u_ {1} u_ {1}}$

e entao

${\ displaystyle {\ begin {alinhados} V ^ {2} & = V ^ {1} + \ phi (x, u, u_ {1}, u_ {2}) {\ frac {\ partial} {\ partial u_ {2}}} \\ & = x {\ frac {\ parcial} {\ parcial u}} - u {\ frac {\ parcial} {\ parcial x}} + (1 + u_ {1} u_ {1} ) {\ frac {\ parcial} {\ parcial u_ {1}}} + \ phi (x, u, u_ {1}, u_ {2}) {\ frac {\ parcial} {\ parcial u_ {2}} } \ end {alinhado}}}$

Portanto, a derivada de Lie da segunda forma de contato em relação a V ² é

${\ displaystyle {\ begin {align} {\ mathcal {L}} _ {V ^ {2}} (\ theta _ {1}) & = {\ mathcal {L}} _ {V ^ {2}} ( du_ {1} -u_ {2} dx) \\ & = {\ mathcal {L}} _ {V ^ {2}} du_ {1} - \ left ({\ mathcal {L}} _ {V ^ { 2}} u_ {2} \ right) dx-u_ {2} \ left ({\ mathcal {L}} _ {V ^ {2}} dx \ right) \\ & = d (V ^ {2} u_ {1}) - V ^ {2} u_ {2} dx-u_ {2} d (V ^ {2} x) \\ & = d (1 + u_ {1} u_ {1}) - \ phi ( x, u, u_ {1}, u_ {2}) dx + u_ {2} du \\ & = 2u_ {1} du_ {1} - \ phi (x, u, u_ {1}, u_ {2} ) dx + u_ {2} du \\ & = 2u_ {1} du_ {1} - \ phi (x, u, u_ {1}, u_ {2}) dx + u_ {2} (\ theta + u_ { 1} dx) & du & = \ theta + u_ {1} dx \\ & = 2u_ {1} (\ theta _ {1} + u_ {2} dx) - \ phi (x, u, u_ {1}, u_ {2}) dx + u_ {2} (\ theta + u_ {1} dx) & du_ {1} & = \ theta _ {1} + u_ {2} dx \\ & = [3u_ {1} u_ {2 } - \ phi (x, u, u_ {1}, u_ {2})] dx + u_ {2} \ theta + 2u_ {1} \ theta _ {1} \ end {alinhado}}}$

Portanto, para preservar o ideal de contato, exigimos ${\ displaystyle {\ mathcal {L}} _ {V ^ {2}} (\ theta _ {1})}$

${\ displaystyle 3u_ {1} u_ {2} - \ phi (x, u, u_ {1}, u_ {2}) = 0 \ quad \ Leftrightarrow \ quad \ phi (x, u, u_ {1}, u_ {2}) = 3u_ {1} u_ {2}.}$

E assim o segundo prolongamento de V para um campo vetorial em J ² (π) é

${\ displaystyle V ^ {2} = x {\ frac {\ partial} {\ partial u}} - u {\ frac {\ partial} {\ partial x}} + (1 + u_ {1} u_ {1} ) {\ frac {\ parcial} {\ parcial u_ {1}}} + 3u_ {1} u_ {2} {\ frac {\ parcial} {\ parcial u_ {2}}}.}$

Observe que o primeiro prolongamento de V pode ser recuperado omitindo os termos da segunda derivada em V ² , ou projetando de volta para J ¹ (π) .

Espaços de jato infinitos

O limite inverso da sequência de projeções dá origem ao espaço de jato infinito J ^∞ (π) . Um ponto é a classe de equivalência das seções de π que têm o mesmo k -jet em p que σ para todos os valores de k . A projeção natural π _{∞ é} mapeada em p . ${\ displaystyle \ pi _ {k + 1, k}: J ^ {k + 1} (\ pi) \ a J ^ {k} (\ pi)}$ ${\ displaystyle j_ {p} ^ {\ infty} (\ sigma)}$${\ displaystyle j_ {p} ^ {\ infty} (\ sigma)}$

Apenas pensando em termos de coordenadas, J ^∞ (π) parece ser um objeto geométrico de dimensão infinita. Na verdade, a maneira mais simples de introduzir uma estrutura diferenciável em J ^∞ (π) , sem depender de gráficos diferenciáveis, é dada pelo cálculo diferencial sobre álgebras comutativas . Dupla à seqüência de projeções de variedades é a seqüência de injeções de álgebras comutativas. Vamos denotar simplesmente por . Considere agora o limite direto de 's. Será uma álgebra comutativa, que pode ser considerada a álgebra de funções suaves sobre o objeto geométrico J ^∞ (π) . Observe que , nascendo como um limite direto, carrega uma estrutura adicional: é uma álgebra comutativa filtrada. ${\ displaystyle \ pi _ {k + 1, k}: J ^ {k + 1} (\ pi) \ a J ^ {k} (\ pi)}$${\ displaystyle \ pi _ {k + 1, k} ^ {*}: C ^ {\ infty} (J ^ {k} (\ pi)) \ para C ^ {\ infty} \ left (J ^ {k +1} (\ pi) \ right)}$${\ displaystyle C ^ {\ infty} (J ^ {k} (\ pi))}$${\ displaystyle {\ mathcal {F}} _ {k} (\ pi)}$ ${\ displaystyle {\ mathcal {F}} (\ pi)}$${\ displaystyle {\ mathcal {F}} _ {k} (\ pi)}$${\ displaystyle {\ mathcal {F}} (\ pi)}$

Grosso modo, um elemento concreto sempre pertencerá a alguns , então é uma função suave na variedade de dimensão finita J ^k (π) no sentido usual. ${\ displaystyle \ varphi \ in {\ mathcal {F}} (\ pi)}$${\ displaystyle {\ mathcal {F}} _ {k} (\ pi)}$

PDEs infinitamente prolongados

Dado um sistema de ordem k de PDEs E ⊆ J ^k (π) , a coleção I (E) de desaparecimento em E funções suaves em J ^∞ (π) é um ideal na álgebra e, portanto, no limite direto . ${\ displaystyle {\ mathcal {F}} _ {k} (\ pi)}$${\ displaystyle {\ mathcal {F}} (\ pi)}$

Aumente I (E) adicionando todas as composições possíveis de derivados totais aplicados a todos os seus elementos. Dessa forma, obtemos um novo ideal I do qual agora está fechado sob a operação de tomar a derivada total. A subvariedade E _(∞) de J ^∞ (π) cortado por eu é chamado o prolongamento infinito de E . ${\ displaystyle {\ mathcal {F}} (\ pi)}$

Geometricamente, E _(∞) é o tubo de distribuição de soluções formais de E . Um ponto de E _(∞) pode ser facilmente visto como sendo representado por uma seção σ cujo gráfico de k -jet é tangente a E no ponto com ordem de tangência arbitrariamente alta. ${\ displaystyle j_ {p} ^ {\ infty} (\ sigma)}$${\ displaystyle j_ {p} ^ {k} (\ sigma)}$

Analiticamente, se E é dado por φ = 0, uma solução formal pode ser entendida como o conjunto de coeficientes de Taylor de uma seção σ em um ponto p que faz desaparecer a série de Taylor de no ponto p . ${\ displaystyle \ varphi \ circ j ^ {k} (\ sigma)}$

Mais importante ainda, as propriedades de fechamento de I implicam que E _(∞) é tangente à estrutura de contato de ordem infinita em J ^∞ (π) , de modo que, ao se restringir a E _(∞), obtém-se a diferença e pode-se estudar o Vinogradov associado Sequência (C-espectral) . ${\ displaystyle {\ mathcal {C}}}$${\ displaystyle {\ mathcal {C}}}$ ${\ displaystyle (E _ {(\ infty)}, {\ mathcal {C}} | _ {E _ {(\ infty)}})}$

Observação

Este artigo definiu jatos de seções locais de um feixe, mas é possível definir jatos de funções f: M → N , onde M e N são variedades; o jato de f então corresponde apenas ao jato da seção

gr _f : M → M × N

gr _f (p) = (p, f (p))

( gr _f é conhecido como o gráfico da função f ) do pacote trivial ( M × N , π ₁ , M ). No entanto, essa restrição não simplifica a teoria, pois a trivialidade global de π não implica a trivialidade global de π ₁ .

Veja também

• Grupo de jato
• Jet (matemática)
• Sistema Lagrangiano
• Bicomplex variacional

Referências

Leitura adicional

• Ehresmann, C., "Introdução à la théorie des structure infinitésimales et des pseudo-groupes de Lie." Geometrie Differentielle, Colloq. Inter. du Centre Nat. de la Recherche Scientifique, Estrasburgo, 1953, 97-127.
• Kolář, I., Michor, P., Slovák, J., Operações naturais em geometria diferencial. Springer-Verlag: Berlin Heidelberg, 1993. ISBN  3-540-56235-4 , ISBN  0-387-56235-4 .
• Saunders, DJ, "The Geometry of Jet Bundles", Cambridge University Press, 1989, ISBN  0-521-36948-7
• Krasil'shchik, IS, Vinogradov, AM, [et al.], "Simetrias e leis de conservação para equações diferenciais de física matemática", Amer. Matemática. Soc., Providence, RI, 1999, ISBN  0-8218-0958-X .
• Olver, PJ , "Equivalence, Invariants and Symmetry", Cambridge University Press, 1995, ISBN  0-521-47811-1
• Giachetta, G., Mangiarotti, L., Sardanashvily, G. , "Advanced Classical Field Theory", World Scientific, 2009, ISBN  978-981-283-895-7
• Sardanashvily, G. , Advanced Differential Geometry for Theoreticians. Fiber bundles, jet manifolds and Lagrangian theory ", Lambert Academic Publishing, 2013, ISBN  978-3-659-37815-7 ; arXiv : 0908.1886