Separador de vértices - Vertex separator

Na teoria dos grafos , um subconjunto de vértices é um separador de vértices (ou corte de vértice , conjunto de separação ) para vértices não adjacentes e se a remoção de do gráfico separa e em componentes conectados distintos . ${\ displaystyle S \ subset V}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle S}$${\ displaystyle a}$${\ displaystyle b}$

Exemplos

Um separador para um gráfico de grade.

Considere um gráfico de grade com r linhas ec colunas; o número total n de vértices é r * c . Por exemplo, na ilustração, r  = 5, c  = 8 e n  = 40. Se r for ímpar, haverá uma única linha central e, caso contrário, haverá duas linhas igualmente próximas do centro; da mesma forma, se c for ímpar, haverá uma única coluna central e, caso contrário, haverá duas colunas igualmente próximas ao centro. Escolher S para ser qualquer uma dessas linhas ou colunas centrais e remover S do gráfico divide o gráfico em dois subgráficos menores conectados A e B , cada um dos quais tem no máximo n / 2 vértices. Se r  ≤  c (como na ilustração), então a escolha de uma coluna central resultará em um separador S com r  ≤ √ n vértices e, da mesma forma, se c  ≤  r , a escolha de uma linha central resultará em um separador com no máximo √ n vértices. Assim, todo gráfico de grade tem um separador S de tamanho no máximo √ n , a remoção do qual o divide em dois componentes conectados, cada um com tamanho no máximo n / 2.

À esquerda uma árvore centrada, à direita uma bicentrada. Os números mostram a excentricidade de cada nó .

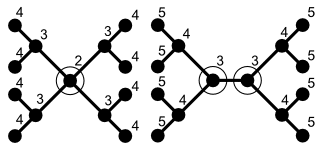
Para dar outra classe de exemplos, toda árvore livre T tem um separador S que consiste em um único vértice, a remoção de que divide T em dois ou mais componentes conectados, cada um com tamanho no máximo n / 2. Mais precisamente, sempre há exatamente um ou exatamente dois vértices, que equivalem a tal separador, dependendo se a árvore é centrada ou bicentrada .

Ao contrário desses exemplos, nem todos os separadores de vértices são balanceados , mas essa propriedade é mais útil para aplicações em ciência da computação, como o teorema do separador planar .

Separadores mínimos

Seja S um (a, b) -separador, ou seja, um subconjunto de vértices que separa dois vértices não adjacentes a e b . Então S é um mínimo (a, b) -separator se nenhum subconjunto apropriado de S separa a e b . Mais geralmente, S é chamado de separador mínimo se for um separador mínimo para algum par (a, b) de vértices não adjacentes. Observe que isso é diferente do conjunto de separação mínimo, que diz que nenhum subconjunto apropriado de S é um separador mínimo (u, v) para qualquer par de vértices (u, v). O seguinte é um resultado bem conhecido que caracteriza os separadores mínimos:

Lema. Um separador de vértices S em G é mínimo se e somente se o gráfico , obtido removendo S de G , tem duas componentes conectadas e tal que cada vértice em S é adjacente a algum vértice em e a algum vértice em . ${\ displaystyle GS}$${\ displaystyle C_ {1}}$${\ displaystyle C_ {2}}$${\ displaystyle C_ {1}}$${\ displaystyle C_ {2}}$

A mínima "(a, b)" - separadores também formar uma estrutura algébrica : Para dois vértices fixos um e B de um dado gráfico G , uma (a, b) -separator S pode ser considerado como um antecessor do outro (a, b) -separator T , se cada caminho de um a b satisfaz S antes de encontrar o t . Mais rigorosamente, a relação predecessora é definida como segue: Sejam S e T dois (a, b) -separadores em 'G'. Em seguida, S é um antecessor de T , em símbolos , se para cada um , a cada caminho que liga X a b satisfaz T . Conclui-se da definição que a relação predecessora produz uma pré - ordem no conjunto de todos os (a, b) -separadores. Além disso, Escalante (1972) mostrou que a relação antecessor dá origem a uma estrutura completa quando restringido ao conjunto de mínimo (a, b) -separators em L . ${\ displaystyle S \ sqsubseteq _ {a, b} ^ {G} T}$${\ displaystyle x \ in S \ setminus T}$

Veja também

• Grafo de cordas , um grafo em que cada separador mínimo é um clique .
• gráfico conectado ao vértice k

Notas

Referências

• Escalante, F. (1972). "Schnittverbände in Graphen". Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg . 38 : 199–220. doi : 10.1007 / BF02996932 .
• George, J. Alan (1973), "Nested dissection of a regular finite element mesh", SIAM Journal on Numerical Analysis , 10 (2): 345-363, doi : 10.1137 / 0710032 , JSTOR   2156361 .
• Golumbic, Martin Charles (1980), Algorithmic Graph Theory and Perfect Graphs , Academic Press, ISBN   0-12-289260-7 .
• Jordan, Camille (1869). "Sur les assemblages de lignes" . Journal für die reine und angewandte Mathematik (em francês). 70 (2): 185–190.
• Rosenberg, Arnold ; Heath, Lenwood (2002). Separadores de gráfico, com aplicativos . Springer. doi : 10.1007 / b115747 .