Normalmente distribuído e não correlacionado não implica independente - Normally distributed and uncorrelated does not imply independent

Na teoria da probabilidade , embora exemplos simples ilustrem que a não correlação linear de duas variáveis ​​aleatórias em geral não implica sua independência , às vezes se pensa erroneamente que isso implica quando as duas variáveis ​​aleatórias são normalmente distribuídas . Este artigo demonstra que a suposição de distribuições normais não tem essa consequência, embora a distribuição normal multivariada , incluindo a distribuição normal bivariada , tenha.

Dizer que o par de variáveis ​​aleatórias tem uma distribuição normal bivariada significa que cada combinação linear de e para coeficientes constantes (ou seja, não aleatórios) e tem uma distribuição normal univariada. Nesse caso, se e não estiverem correlacionados, eles são independentes. No entanto, é possível que duas variáveis aleatórias e para ser distribuído em conjunto de modo que cada uma por si só é marginalmente normalmente distribuída, e eles não estão correlacionados, mas eles não são independentes; exemplos são dados abaixo. ${\ displaystyle (X, Y)}$ ${\ displaystyle aX + bY}$${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle X}$${\ displaystyle Y}$

Exemplos

Um exemplo simétrico

Gama conjunta de e . Mais escuro indica um valor mais alto da função de densidade.${\ displaystyle X}$${\ displaystyle Y}$

Suponha que tenha uma distribuição normal com valor esperado 0 e variância 1. Deixe ter a distribuição de Rademacher , de modo que ou , cada um com probabilidade 1/2, e suponha que seja independente de . Deixe . Então ${\ displaystyle X}$${\ displaystyle W}$${\ displaystyle W = 1}$${\ displaystyle W = -1}$${\ displaystyle W}$${\ displaystyle X}$${\ displaystyle Y = WX}$

• ${\ displaystyle X}$e não estão correlacionados;${\ displaystyle Y}$
• ambos têm a mesma distribuição normal; e
• ${\ displaystyle X}$e não são independentes.${\ displaystyle Y}$

Para ver isso e não estão correlacionados, pode-se considerar a covariância : por definição, é ${\ displaystyle X}$${\ displaystyle Y}$ ${\ displaystyle \ operatorname {cov} (X, Y)}$

${\ displaystyle \ operatorname {cov} (X, Y) = \ operatorname {E} (XY) - \ operatorname {E} (X) \ operatorname {E} (Y).}$

Então, por definição das variáveis aleatórias , e , ea independência do de , um tem ${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle W}$${\ displaystyle W}$${\ displaystyle X}$

${\ displaystyle \ operatorname {cov} (X, Y) = \ operatorname {E} (XY) -0 = \ operatorname {E} (X ^ {2} W) = \ operatorname {E} (X ^ {2} ) \ operatorname {E} (W) = \ operatorname {E} (X ^ {2}) \ cdot 0 = 0.}$

Para ver que tem a mesma distribuição normal que , considere ${\ displaystyle Y}$${\ displaystyle X}$

${\ displaystyle {\ begin {alinhado} \ Pr (Y \ leq x) & {} = \ operatorname {E} (\ Pr (Y \ leq x \ mid W)) \\ & {} = \ Pr (X \ leq x) \ Pr (W = 1) + \ Pr (-X \ leq x) \ Pr (W = -1) \\ & {} = \ Phi (x) \ cdot {\ frac {1} {2} } + \ Phi (x) \ cdot {\ frac {1} {2}} \ end {alinhado}}}$

(uma vez que e ambos têm a mesma distribuição normal), onde é a função de distribuição cumulativa da distribuição normal padrão. ${\ displaystyle X}$${\ displaystyle -X}$${\ displaystyle \ Phi (x)}$

Para ver isso e não ser independente, observe isso ou aquilo . ${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle | Y | = | X |}$${\ displaystyle \ operatorname {Pr} (Y> 1 | X = 1/2) = \ operatorname {Pr} (X> 1 | X = 1/2) = 0}$

Finalmente, a distribuição da combinação linear simples concentra probabilidade positiva a 0: . Portanto, a variável aleatória não é normalmente distribuída e, portanto, também e não é normalmente distribuída em conjunto (pela definição acima). ${\ displaystyle X + Y}$${\ displaystyle \ operatorname {Pr} (X + Y = 0) = 1/2}$${\ displaystyle X + Y}$${\ displaystyle X}$${\ displaystyle Y}$

Um exemplo assimétrico

A densidade conjunta de e . Mais escuro indica um valor mais alto de densidade.${\ displaystyle X}$${\ displaystyle Y}$

Suponha que tenha uma distribuição normal com valor esperado 0 e variância 1. Deixe ${\ displaystyle X}$

${\ displaystyle Y = \ left \ {{\ begin {matrix} X & {\ text {if}} \ left | X \ right | \ leq c \\ - X & {\ text {if}} \ left | X \ right |> c \ end {matriz}} \ direita.}$

onde é um número positivo a ser especificado abaixo. Se for muito pequeno, então a correlação será próxima se for muito grande, então será próximo a 1. Uma vez que a correlação é uma função contínua de , o teorema do valor intermediário implica que existe algum valor particular de que torna a correlação 0. Esse valor é aproximadamente 1,54. Nesse caso, e não são correlacionados, mas eles claramente não são independentes, uma vez que determina completamente . ${\ displaystyle c}$${\ displaystyle c}$ ${\ displaystyle \ operatorname {corr} (X, Y)}$${\ displaystyle -1}$${\ displaystyle c}$${\ displaystyle \ operatorname {corr} (X, Y)}$${\ displaystyle c}$${\ displaystyle c}$${\ displaystyle X}$${\ displaystyle Y}$${\ displaystyle X}$${\ displaystyle Y}$

Para ver que é normalmente distribuído - na verdade, que sua distribuição é a mesma de - alguém pode calcular sua função de distribuição cumulativa : ${\ displaystyle Y}$${\ displaystyle X}$

${\ displaystyle {\ begin {alinhados} \ Pr (Y \ leq x) & = \ Pr (\ {| X | \ leq c {\ text {e}} X \ leq x \} {\ text {ou}} \ {| X |> c {\ text {e}} - X \ leq x \}) \\ & = \ Pr (| X | \ leq c {\ text {e}} X \ leq x) + \ Pr (| X |> c {\ texto {e}} - X \ leq x) \\ & = \ Pr (| X | \ leq c {\ texto {e}} X \ leq x) + \ Pr (| X |> c {\ text {e}} X \ leq x) \\ & = \ Pr (X \ leq x), \ end {alinhado}}}$

onde a penúltima igualdade segue da simetria da distribuição de e da simetria da condição que . ${\ displaystyle X}$${\ displaystyle | X | \ leq c}$

Neste exemplo, a diferença está longe de ser normalmente distribuída, uma vez que tem uma probabilidade substancial (cerca de 0,88) de ser igual a 0. Em contraste, a distribuição normal, sendo uma distribuição contínua, não tem parte discreta, isto é, ele não concentra mais do que probabilidade zero em qualquer ponto único. Conseqüentemente, e não são normalmente distribuídos em conjunto , embora sejam normalmente distribuídos separadamente. ${\ displaystyle XY}$${\ displaystyle X}$${\ displaystyle Y}$

Exemplos com suporte em quase todos os lugares em ℝ ²

É bem conhecido que a proporção de dois desvios aleatórios normais padrão independentes e tem uma distribuição de Cauchy . Pode-se igualmente começar com a variável aleatória de Cauchy e derivar a distribuição condicional de para satisfazer o requisito de que com e independente e normal padrão. Passando pela matemática, descobrimos que ${\ displaystyle C}$${\ displaystyle X_ {i}}$${\ displaystyle Y_ {i}}$${\ displaystyle C}$${\ displaystyle Y_ {i}}$${\ displaystyle X_ {i} = CY_ {i}}$${\ displaystyle X_ {i}}$${\ displaystyle Y_ {i}}$

${\ displaystyle Y_ {i} = W_ {i} {\ sqrt {\ frac {\ chi _ {i} ^ {2} \ left (k = 2 \ right)} {1 + C ^ {2}}}} }$

em que é uma variável aleatória Rademacher e é uma variável aleatória Qui-quadrado com dois graus de liberdade. ${\ displaystyle W_ {i}}$${\ displaystyle \ chi _ {i} ^ {2} \ left (k = 2 \ right)}$

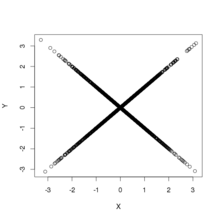
Considere dois conjuntos de , . Observe que não é indexado por - ou seja, a mesma variável aleatória de Cauchy é usada na definição de e . Este compartilhamento de resultados em dependências entre os índices: nem, nem é independente de . No entanto, todos os e não estão correlacionados como as distribuições bivariadas têm simetria de reflexão ao longo dos eixos. ${\ displaystyle \ left (X_ {i}, Y_ {i} \ right)}$${\ displaystyle i \ in \ left \ {1,2 \ right \}}$${\ displaystyle C}$${\ displaystyle i}$${\ displaystyle C}$${\ displaystyle \ left (X_ {1}, Y_ {1} \ right)}$${\ displaystyle \ left (X_ {2}, Y_ {2} \ right)}$${\ displaystyle C}$${\ displaystyle X_ {1}}$${\ displaystyle Y_ {1}}$${\ displaystyle Y_ {2}}$${\ displaystyle X_ {i}}$${\ displaystyle Y_ {i}}$

Distribuições conjuntas não normais com marginais normais.

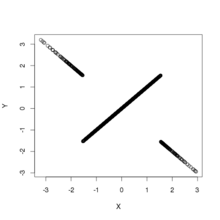
A figura mostra gráficos de dispersão de amostras retiradas da distribuição acima. Isso fornece dois exemplos de distribuições bivariadas que não são correlacionadas e têm distribuições marginais normais, mas não são independentes. O painel esquerdo mostra a distribuição conjunta de e ; a distribuição tem suporte em todos os lugares, menos na origem. O painel direito mostra a distribuição conjunta de e ; a distribuição tem suporte em todos os lugares, exceto ao longo dos eixos e tem uma descontinuidade na origem: a densidade diverge quando a origem é abordada por qualquer caminho reto, exceto ao longo dos eixos. ${\ displaystyle X_ {1}}$${\ displaystyle Y_ {2}}$${\ displaystyle Y_ {1}}$${\ displaystyle Y_ {2}}$

Veja também

• Correlação e dependência

Referências

Notas