Estrutura de dados com conjuntos separados - Disjoint-set data structure

Disjoint-set / Union-find Forest
Disjoint-set / Union-find Forest
Modelo	árvore multiway
Inventado	1964
Inventado por	Bernard A. Galler e Michael J. Fischer
Complexidade de tempo em notação grande O

MakeSet cria 8 singletons.

Após algumas operações de Union, alguns conjuntos são agrupados.

Na ciência da computação , uma estrutura de dados de conjunto disjunto , também chamada de estrutura de dados de localização de união ou conjunto de localização de mesclagem , é uma estrutura de dados que armazena uma coleção de conjuntos de desconexão (não sobrepostos). De forma equivalente, ele armazena uma partição de um conjunto em subconjuntos separados. Ele fornece operações para adicionar novos conjuntos, mesclar conjuntos (substituindo-os por sua união ) e encontrar um membro representante de um conjunto. A última operação permite descobrir de forma eficiente se quaisquer dois elementos estão no mesmo conjunto ou em conjuntos diferentes.

Embora existam várias maneiras de implementar estruturas de dados com conjuntos separados, na prática, elas são frequentemente identificadas com uma implementação específica chamada floresta com conjuntos separados . Este é um tipo especializado de floresta que realiza uniões e encontra em tempo amortizado quase constante. Para realizar uma sequência de $m$ adição, união ou operações de localização em uma floresta com conjuntos disjuntos com $n$ nós, é necessário tempo total $O (m α (n))$ , onde $α (n)$ é a função inversa de Ackermann de crescimento extremamente lento . Florestas separadas não garantem esse desempenho por operação. As operações individuais de união e localização podem levar mais tempo do que um tempo constante de tempo $α (n)$ , mas cada operação faz com que a floresta disjunta se ajuste para que as operações sucessivas sejam mais rápidas. Florestas disjuntas são assintoticamente ótimas e praticamente eficientes.

Estruturas de dados com conjuntos separados desempenham um papel fundamental no algoritmo de Kruskal para encontrar a árvore de abrangência mínima de um gráfico. A importância das árvores geradoras mínimas significa que estruturas de dados com conjuntos separados são a base de uma ampla variedade de algoritmos. Além disso, estruturas de dados com conjuntos separados também têm aplicações para computação simbólica, bem como em compiladores, especialmente para problemas de alocação de registradores .

História

Florestas disjuntos-estabelecidos foram descritos pela primeira vez por Bernard R. Galler e Michael J. Fischer em 1964. Em 1973, a sua complexidade de tempo foi limitado a , o logaritmo iterado de , por Hopcroft e Ullman . Em 1975, Robert Tarjan foi o primeiro a provar o limite superior ( função de Ackermann inversa ) na complexidade de tempo do algoritmo e, em 1979, mostrou que este era o limite inferior para um caso restrito. Em 1989, Fredman e Saks mostraram que palavras (amortizadas) devem ser acessadas por qualquer estrutura de dados conjunto disjunta por operação, provando assim a otimalidade da estrutura de dados. ${\ displaystyle O (\ log ^ {*} (n))}$ ${\ displaystyle n}$ ${\ displaystyle O (m \ alpha (n))}$ ${\ displaystyle \ Omega (\ alpha (n))}$

Em 1991, Galil e Italiano publicaram um levantamento das estruturas de dados para conjuntos disjuntos.

Em 1994, Richard J. Anderson e Heather Woll descreveram uma versão paralela do Union – Find que nunca precisa ser bloqueada.

Em 2007, Sylvain Conchon e Jean-Christophe Filliâtre desenvolveram uma versão persistente da estrutura de dados florestais disjuntos, permitindo que versões anteriores da estrutura fossem retidas de forma eficiente, e formalizou sua correção usando o assistente de prova Coq . No entanto, a implementação só é assintótica se usada de forma efêmera ou se a mesma versão da estrutura for usada repetidamente com retrocesso limitado.

Representação

Cada nó em uma floresta com conjuntos separados consiste em um ponteiro e algumas informações auxiliares, um tamanho ou uma classificação (mas não ambos). Os ponteiros são usados para fazer árvores de ponteiros pais , onde cada nó que não é a raiz de uma árvore aponta para seu pai. Para distinguir os nós raiz de outros, seus ponteiros pais têm valores inválidos, como uma referência circular ao nó ou um valor sentinela. Cada árvore representa um conjunto armazenado na floresta, com os membros do conjunto sendo os nós da árvore. Os nós raiz fornecem representantes de conjunto: dois nós estão no mesmo conjunto se e somente se as raízes das árvores que contêm os nós forem iguais.

Os nós na floresta podem ser armazenados de qualquer maneira conveniente para o aplicativo, mas uma técnica comum é armazená-los em um array. Nesse caso, os pais podem ser indicados por seu índice de matriz. Cada entrada de array requer $Θ (lg n)$ bits de armazenamento para o ponteiro pai. Uma quantidade comparável ou menor de armazenamento é necessária para o resto da entrada, então o número de bits necessários para armazenar a floresta é $Θ (n lg n)$ . Se uma implementação usa nós de tamanho fixo (limitando assim o tamanho máximo da floresta que pode ser armazenado), então o armazenamento necessário é linear em $n$ .

Operações

Estruturas de dados de conjuntos separados suportam três operações: fazer um novo conjunto contendo um novo elemento; Encontrar o representante do conjunto que contém um determinado elemento; e mesclando dois conjuntos.

Fazendo novos conjuntos

A MakeSetoperação adiciona um novo elemento. Este elemento é colocado em um novo conjunto contendo apenas o novo elemento, e o novo conjunto é adicionado à estrutura de dados. Se, em vez disso, a estrutura de dados for vista como uma partição de um conjunto, a MakeSetoperação amplia o conjunto adicionando o novo elemento e estende a partição existente colocando o novo elemento em um novo subconjunto contendo apenas o novo elemento.

Em uma floresta com conjuntos separados, MakeSetinicializa o ponteiro pai do nó e o tamanho ou classificação do nó. Se uma raiz for representada por um nó que aponta para si mesmo, a adição de um elemento pode ser descrita usando o seguinte pseudocódigo:

function MakeSet(x) is
    if x is not already in the forest then
        x.parent := x
        x.size := 1     // if nodes store size
        x.rank := 0     // if nodes store rank
    end if
end function

Esta operação tem complexidade de tempo constante. Em particular, inicializar uma floresta com conjuntos separados com $n$ nós requer tempo $O (n)$ .

Na prática, MakeSetdeve ser precedido por uma operação que aloca memória para conter $x$ . Contanto que a alocação de memória seja uma operação de tempo constante amortizado, como é para uma boa implementação de array dinâmico , ela não altera o desempenho assintótico da floresta de conjuntos aleatórios.

Encontrar representantes de conjuntos

A Findoperação segue a cadeia de ponteiros pais de um nó de consulta especificado $x$ até atingir um elemento raiz. Este elemento raiz representa o conjunto ao qual $x$ pertence e pode ser o próprio $x$ . Findretorna o elemento raiz que atinge.

A realização de uma Findoperação apresenta uma oportunidade importante para o aprimoramento da floresta. O tempo em uma Findoperação é gasto perseguindo ponteiros pais, portanto, uma árvore mais plana leva a Findoperações mais rápidas . Quando a Findé executado, não há maneira mais rápida de alcançar a raiz do que seguir cada ponteiro pai em sucessão. No entanto, os ponteiros pais visitados durante esta pesquisa podem ser atualizados para apontar mais perto da raiz. Como cada elemento visitado no caminho para a raiz faz parte do mesmo conjunto, isso não altera os conjuntos armazenados na floresta. Mas torna as Findoperações futuras mais rápidas, não apenas para os nós entre o nó de consulta e a raiz, mas também para seus descendentes. Essa atualização é uma parte importante da garantia de desempenho amortizada da floresta desconexa.

Existem vários algoritmos para Findatingir a complexidade de tempo assintoticamente ideal. Uma família de algoritmos, conhecida como compactação de caminho , faz com que cada nó entre o nó de consulta e o ponto raiz até a raiz. A compactação de caminho pode ser implementada usando uma recursão simples da seguinte maneira:

function Find(x) is
    if x.parent ≠ x then
        x.parent := Find(x.parent)
        return x.parent
    else
        return x
    end if
end function

Essa implementação faz duas passagens, uma para cima na árvore e outra para baixo. Ele requer memória temporária suficiente para armazenar o caminho do nó de consulta até a raiz (no pseudocódigo acima, o caminho é representado implicitamente usando a pilha de chamadas). Isso pode ser reduzido para uma quantidade constante de memória, executando os dois passes na mesma direção. A implementação de memória constante vai do nó de consulta à raiz duas vezes, uma para encontrar a raiz e outra para atualizar os ponteiros:

function Find(x) is
    root := x
    while root.parent ≠ root do
        root := root.parent
    end while

    while x.parent ≠ root do
        parent := x.parent
        x.parent := root
        x := parent
    end while

    return root
end function

Tarjan e Van Leeuwen também desenvolveram Findalgoritmos de passagem única que mantêm a mesma complexidade de pior caso, mas são mais eficientes na prática. Estes são chamados de divisão de caminho e divisão de caminho pela metade. Ambos atualizam os ponteiros pais dos nós no caminho entre o nó da consulta e a raiz. A divisão de caminho substitui cada ponteiro pai nesse caminho por um ponteiro para o avô do nó:

function Find(x) is
    while x.parent ≠ x do
        (x, x.parent) := (x.parent, x.parent.parent)
    end while
    return x
end function

A divisão do caminho pela metade funciona de maneira semelhante, mas substitui apenas todos os outros ponteiros pai:

function Find(x) is
    while x.parent ≠ x do
        x.parent := x.parent.parent
        x := x.parent
    end while
    return x
end function

Mesclando dois conjuntos

A operação substitui o conjunto que contém $xe$ o conjunto que contém $y$ por sua união. primeiros usos para determinar as raízes de árvores que contenham $x$ e $y$ . Se as raízes são as mesmas, não há mais nada a fazer. Caso contrário, as duas árvores devem ser fundidas. Isso é feito definindo o ponteiro pai de $x$ para $y$ ou definindo o ponteiro pai de $y$ para $x$ . Union(x, y)UnionFind

A escolha de qual nó se torna o pai tem consequências para a complexidade das operações futuras na árvore. Se isso for feito sem cuidado, as árvores podem se tornar excessivamente altas. Por exemplo, suponha que Unionsempre fez da árvore que contém $x$ uma subárvore da árvore que contém $y$ . Comece com uma floresta que acaba de ser inicializado com elementos e executar , , ..., . A floresta resultante contém uma única árvore cuja raiz é $n$ , e o caminho de 1 a $n$ passa por todos os nós da árvore. Para esta floresta, o tempo de execução é $O$ $($ $n$ $)$ . ${\ displaystyle 1,2,3, \ ldots, n,}$ $Union(1, 2)$ $Union(2, 3)$ $Union(n - 1, n)$ Find(1)

Em uma implementação eficiente, a altura da árvore é controlada usando união por tamanho ou união por classificação . Ambos requerem que um nó armazene informações além de apenas seu ponteiro pai. Essas informações são usadas para decidir qual raiz se tornará o novo pai. Ambas as estratégias garantem que as árvores não se tornem muito profundas.

No caso de união por tamanho, um nó armazena seu tamanho, que é simplesmente seu número de descendentes (incluindo o próprio nó). Quando as árvores com raízes $x$ e $y$ são fundidas, o nó com o mais descendentes se torna o pai. Se os dois nós tiverem o mesmo número de descendentes, então qualquer um pode se tornar o pai. Em ambos os casos, o tamanho do novo nó pai é definido como seu novo número total de descendentes.

function Union(x, y) is
    // Replace nodes by roots
    x := Find(x)
    y := Find(y)

    if x = y then
        return  // x and y are already in the same set
    end if

    // If necessary, rename variables to ensure that
    // x has at least as many descendants as y
    if x.size < y.size then
        (x, y) := (y, x)
    end if

    // Make x the new root
    y.parent := x
    // Update the size of x
    x.size := x.size + y.size
end function

O número de bits necessários para armazenar o tamanho é claramente o número de bits necessários para armazenar $n$ . Isso adiciona um fator constante ao armazenamento necessário da floresta.

Para união por classificação, um nó armazena sua classificação , que é um limite superior para sua altura. Quando um nó é inicializado, sua classificação é definida como zero. Para mesclar árvores com raízes $x$ e $y$ , primeiro comparar suas fileiras. Se as fileiras são diferentes, então o posto árvore maior se torna o pai, e as fileiras de $x$ e $y$ não mudam. Se as classificações forem iguais, qualquer um pode se tornar o pai, mas a classificação do novo pai é incrementada em um. Embora a classificação de um nó esteja claramente relacionada à sua altura, armazenar classificações é mais eficiente do que armazenar alturas. A altura de um nó pode mudar durante uma Findoperação, portanto, o armazenamento de classificações evita o esforço extra de manter a altura correta. Em pseudocódigo, união por classificação é:

function Union(x, y) is
    // Replace nodes by roots
    x := Find(x)
    y := Find(y)

    if x = y then
        return  // x and y are already in the same set
    end if

    // If necessary, rename variables to ensure that
    // x has rank at least as large as that of y
    if x.rank < y.rank then
        (x, y) := (y, x)
    end if

    // Make x the new root
    y.parent := x
    // If necessary, increment the rank of x
    if x.rank = y.rank then
        x.rank := x.rank + 1
    end if
end function

Pode-se mostrar que cada nó tem classificação ou menos. Consequentemente, a classificação pode ser armazenada em bits $O$ $(log$ $n$ $)$ , tornando-a uma parte assintoticamente insignificante do tamanho da floresta. ${\ displaystyle \ lfloor \ lg n \ rfloor}$

É claro a partir das implementações acima que o tamanho e a classificação de um nó não importam, a menos que um nó seja a raiz de uma árvore. Depois que um nó se torna filho, seu tamanho e classificação nunca são acessados novamente.

Complexidade de tempo

Uma implementação de floresta com conjunto disjunto na qual Findnão atualiza os ponteiros pai e na qual Unionnão tenta controlar as alturas das árvores, pode ter árvores com altura $O (n)$ . Em tal situação, as operações Finde Unionrequerem tempo $O (n)$ .

Se uma implementação usar apenas a compactação de caminho, uma sequência de $n$ MakeSet operações, seguida por até $n - 1$ Union operações $ef$ Find operações, terá um tempo de execução de pior caso de . ${\ displaystyle \ Theta (n + f \ cdot \ left (1+ \ log _ {2 + f / n} n \ right))}$

Usar união por classificação, mas sem atualizar os ponteiros pai durante Find, dá um tempo de execução de operações for $m$ de qualquer tipo, até $n$ das quais são operações. ${\ displaystyle \ Theta (m \ log n)}$ MakeSet

A combinação de compactação, divisão ou divisão de caminho, com união por tamanho ou classificação, reduz o tempo de execução de $m$ operações de qualquer tipo, até $n$ das quais são MakeSetoperações para . Isso torna o tempo de execução amortizado de cada operação . Isso é assintoticamente ideal, o que significa que cada estrutura de dados de conjunto disjunta deve usar o tempo amortizado por operação. Aqui, a função é a função inversa de Ackermann . A função inversa de Ackermann cresce extraordinariamente devagar, então esse fator é $4$ ou menos para qualquer $n$ que possa realmente ser escrito no universo físico. Isso faz com que as operações disjuntas sejam praticamente amortizadas em tempo constante. ${\ displaystyle \ Theta (m \ alpha (n))}$ ${\ displaystyle \ Theta (\ alpha (n))}$ ${\ displaystyle \ Omega (\ alpha (n))}$ ${\ displaystyle \ alpha (n)}$

Prova de complexidade de tempo O (log * (n)) de Union-Find

A análise precisa do desempenho de uma floresta desconexa é um tanto intrincada. No entanto, há uma análise muito mais simples que prova que o tempo amortizado para quaisquer $m$ Find ou Unionoperações em uma floresta disjunta contendo $n$ objetos é $O (mlog * n)$ , onde $log *$ denota o logaritmo iterado .

Lema 1: À medida que a função find segue o caminho até a raiz, a classificação do nó que encontra está aumentando.

Prova: alegar que, à medida que as operações Find e Union são aplicadas ao conjunto de dados, esse fato permanece verdadeiro ao longo do tempo. Inicialmente, quando cada nó é a raiz de sua própria árvore, isso é trivialmente verdadeiro. O único caso em que a classificação de um nó pode ser alterada é quando a operação União por Classificação é aplicada. Nesse caso, uma árvore com classificação menor será anexada a uma árvore com classificação maior, ao invés do contrário. E durante a operação de localização, todos os nós visitados ao longo do caminho serão anexados à raiz, que tem uma classificação maior do que seus filhos, portanto, essa operação também não mudará esse fato.

Lema 2: Um nó $u$ que é a raiz de uma subárvore com classificação $r$ tem pelo menos nós. ${\ displaystyle 2 ^ {r}}$

Prova: Inicialmente, quando cada nó é a raiz de sua própria árvore, isso é trivialmente verdadeiro. Suponha que um nó

u

com classificação

r

tenha pelo menos

2 r

nós. Então, quando duas árvores com classificação

r

são fundidas usando a operação União por Classificação , resulta uma árvore com classificação

r + 1

, cuja raiz tem pelo menos nós.

{\ displaystyle 2 ^ {r} + 2 ^ {r} = 2 ^ {r + 1}}

Lema 3: O número máximo de nós de classificação $r$ é no máximo ${\ displaystyle {\ frac {n} {2 ^ {r}}}.}$

Prova: a partir do lema 2 , sabemos que um nó

u

que é a raiz de uma subárvore com posto

r

tem pelo menos nós. Obteremos o número máximo de nós de classificação

r

quando cada nó com classificação

r

for a raiz de uma árvore que possui exatamente nós. Neste caso, o número de nós de classificação

r

é

{\ displaystyle 2 ^ {r}}

{\ displaystyle 2 ^ {r}}

{\ displaystyle {\ frac {n} {2 ^ {r}}}.}

Por conveniência, definimos "bucket" aqui: um bucket é um conjunto que contém vértices com classificações específicas.

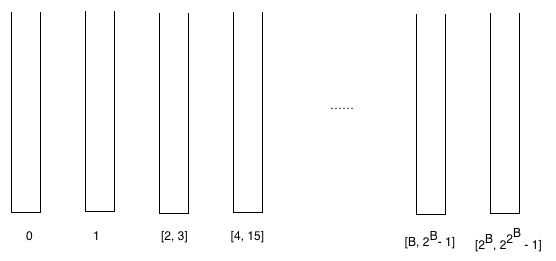
Nós criamos alguns baldes e colocamos vértices nos baldes de acordo com suas classificações indutivamente. Ou seja, vértices com classificação 0 vão para o balde zero, vértices com classificação 1 vão para o primeiro balde, vértices com classificação 2 e 3 vão para o segundo balde. Se o $B$ ^th balde contém vértices com fileiras de intervalo , em seguida, o (B + 1) r balde conterá vértices com fileiras de intervalo ${\ displaystyle \ left [r, 2 ^ {r} -1 \ right] = [r, R-1]}$ ${\ displaystyle \ left [R, 2 ^ {R} -1 \ right].}$

Prova de Encontro de União

{\ displaystyle O (\ log ^ {*} n)}

Podemos fazer duas observações sobre os baldes.

O número total de depósitos é no máximo $log * n$
Prova: Quando vamos de um balde para o próximo, adicionamos mais um dois à potência, ou seja, o próximo balde a será ${\ displaystyle \ left [B, 2 ^ {B} -1 \ right]}$ ${\ displaystyle \ left [2 ^ {B}, 2 ^ {2 ^ {B}} - 1 \ right]}$
O número máximo de elementos no intervalo é no máximo ${\ displaystyle \ left [B, 2 ^ {B} -1 \ right]}$ ${\ displaystyle {\ frac {2n} {2 ^ {B}}}}$
Prova: O número máximo de elementos no intervalo é no máximo ${\ displaystyle \ left [B, 2 ^ {B} -1 \ right]}$ ${\ displaystyle {\ frac {n} {2 ^ {B}}} + {\ frac {n} {2 ^ {B + 1}}} + {\ frac {n} {2 ^ {B + 2}} } + \ cdots + {\ frac {n} {2 ^ {2 ^ {B} -1}}} \ leq {\ frac {2n} {2 ^ {B}}}.}$

Deixe $F$ representar a lista de operações "encontrar" realizadas, e deixe

{\ displaystyle T_ {1} = \ sum _ {F} {\ text {(link para a raiz)}}}

{\ displaystyle T_ {2} = \ sum _ {F} {\ text {(número de links percorridos onde os blocos são diferentes)}}}

{\ displaystyle T_ {3} = \ sum _ {F} {\ text {(número de links percorridos onde os blocos são iguais).}}}

Então, o custo total de $m$ achados é ${\ displaystyle T = T_ {1} + T_ {2} + T_ {3}.}$

Como cada operação de localização faz exatamente um percurso que leva a uma raiz, temos $T 1 = O (m)$ .

Além disso, do limite acima sobre o número de intervalos, temos $T 2 = O (m log * n)$ .

Para $T 3$ , suponhamos que são atravessando uma aresta de $u$ para $v$ , onde $u$ e $v$ têm classificação no balde $[B, 2 B - 1]$ e $v$ não é a raiz (no momento deste deslocamento, caso contrário o percurso seria ser contabilizado em $T 1$ ). Fixe $u$ e considere a sequência que assume o papel de $v$ em diferentes operações de localização. Por causa da compressão do caminho e não levar em conta a borda de uma raiz, esta sequência contém apenas nós diferentes e, por causa do Lema 1 , sabemos que as classificações dos nós nesta sequência estão estritamente aumentando. Por ambos os nós estarem no intervalo, podemos concluir que o comprimento $k$ da sequência (o número de vezes que o nó $u$ está ligado a uma raiz diferente no mesmo intervalo) é no máximo o número de classificações nos intervalos $B$ , que é, no máximo ${\ displaystyle v_ {1}, v_ {2}, \ ldots, v_ {k}}$ ${\ displaystyle 2 ^ {B} -1-B <2 ^ {B}.}$

Portanto, ${\ displaystyle T_ {3} \ leq \ sum _ {[B, 2 ^ {B} -1]} \ sum _ {u} 2 ^ {B}.}$

Das Observações 1 e 2 , podemos concluir que ${\ displaystyle T_ {3} \ leq \ sum _ {B} 2 ^ {B} {\ frac {2n} {2 ^ {B}}} \ leq 2n \ log ^ {*} n.}$

Portanto, ${\ displaystyle T = T_ {1} + T_ {2} + T_ {3} = O (m \ log ^ {*} n).}$

Formulários

Uma demonstração para Union-Find ao usar o algoritmo de Kruskal para encontrar a árvore de abrangência mínima.

Estruturas de dados de conjuntos separados modelam o particionamento de um conjunto , por exemplo, para rastrear os componentes conectados de um gráfico não direcionado . Este modelo pode então ser usado para determinar se dois vértices pertencem ao mesmo componente ou se adicionar uma aresta entre eles resultaria em um ciclo. O algoritmo Union-Find é usado em implementações de unificação de alto desempenho .

Esta estrutura de dados é usada pela Boost Graph Library para implementar sua funcionalidade Incremental Connected Components . É também um componente chave na implementação do algoritmo de Kruskal para encontrar a árvore de abrangência mínima de um gráfico.

Observe que a implementação como florestas com conjuntos separados não permite a exclusão de arestas, mesmo sem compactação de caminho ou heurística de classificação.

Sharir e Agarwal relatam conexões entre o pior caso de comportamento de conjuntos disjuntos e o comprimento das sequências de Davenport-Schinzel , uma estrutura combinatória da geometria computacional.

Veja também

Refinamento de partição , uma estrutura de dados diferente para manter conjuntos separados, com atualizações que dividem conjuntos em vez de mesclá-los.
Conectividade dinâmica

Languages

In other projects