Cardioide - Cardioid

Um cardióide (do grego καρδία "coração") é uma curva plana traçada por um ponto no perímetro de um círculo que está rolando em torno de um círculo fixo do mesmo raio. O grego sugere ainda que o movimento dessa rotação imita o balanço do coração em um eixo definido matematicamente como cardióide. Também pode ser definido como um epiciclóide com uma única cúspide . É também um tipo de espiral sinusoidal e uma curva inversa da parábola com o foco como centro de inversão. É também o conjunto de pontos de reflexos de um ponto fixo em um círculo por todas as tangentes ao círculo.

O nome foi cunhado por de Castillon em 1741, mas tinha sido objeto de estudo décadas antes. Nomeado por sua forma semelhante a um coração, é mais parecido com o contorno da seção transversal de uma maçã redonda sem o pedúnculo.

Um microfone cardióide exibe um padrão de captação acústica que, quando representado em duas dimensões, se assemelha a um cardióide (qualquer plano 2d contendo a linha reta 3d do corpo do microfone). Em três dimensões, o cardióide tem a forma de uma maçã centrada em torno do microfone, que é o "pedúnculo" da maçã.

Equações

Let Ser o raio comum dos dois círculos geradores com pontos médios , o ângulo de rolamento e a origem o ponto de partida (veja a imagem). Um pega o ${\ displaystyle a}$${\ displaystyle (-a, 0), (a, 0)}$${\ displaystyle \ varphi}$

• representação paramétrica :

${\ displaystyle x (\ varphi) = 2a (1- \ cos \ varphi) \ cdot \ cos \ varphi \,}$

${\ displaystyle y (\ varphi) = 2a (1- \ cos \ varphi) \ cdot \ sin \ varphi \, \ qquad 0 \ leq \ varphi <2 \ pi}$

e daqui a representação em

• coordenadas polares :

${\ displaystyle r (\ varphi) = 2a (1- \ cos \ varphi)}$.

Apresentando as substituições e obtém-se depois de remover a raiz quadrada a representação implícita em ${\ displaystyle \ cos \ varphi = x / r}$${\ displaystyle r = {\ sqrt {x ^ {2} + y ^ {2}}}}$

• coordenadas cartesianas :

${\ displaystyle (x ^ {2} + y ^ {2}) ^ {2} + 4ax (x ^ {2} + y ^ {2}) - 4a ^ {2} y ^ {2} \, = \ , 0}$ .

Prova para a representação paramétrica

Uma prova pode ser estabelecida usando números complexos e sua descrição comum como o plano complexo . O movimento de rolamento do círculo preto sobre o azul pode ser dividido em duas rotações. No plano complexo, uma rotação em torno do ponto (a origem) por um ângulo pode ser realizada multiplicando um ponto (número complexo) por . Portanto ${\ displaystyle 0}$${\ displaystyle \ varphi}$${\ displaystyle z}$${\ displaystyle e ^ {i \ varphi}}$

a rotação em torno do ponto é ,${\ displaystyle \ Phi _ {+}}$${\ displaystyle a}$${\ displaystyle: z \ mapsto a + (za) e ^ {i \ varphi}}$

a rotação em torno do ponto é: .${\ displaystyle \ Phi _ {-}}$${\ displaystyle -a}$${\ displaystyle z \ mapsto -a + (z + a) e ^ {i \ varphi}}$

Um ponto do cardióide é gerado girando a origem em torno do ponto e, subsequentemente, girando no mesmo ângulo : ${\ displaystyle p (\ varphi)}$${\ displaystyle a}$${\ displaystyle -a}$${\ displaystyle \ varphi}$

${\ displaystyle p (\ varphi) = \ Phi _ {-} (\ Phi _ {+} (0)) = \ Phi _ {-} (a-ae ^ {i \ varphi}) = - a + (a- ae ^ {i \ varphi} + a) e ^ {i \ varphi} = a \; (- e ^ {i2 \ varphi} + 2e ^ {i \ varphi} -1)}$.

A partir daqui, obtém-se a representação paramétrica acima:

${\ displaystyle {\ begin {array} {cclcccc} x (\ varphi) & = & a \; (- \ cos (2 \ varphi) +2 \ cos \ varphi -1) & = & 2a (1- \ cos \ varphi ) \ cdot \ cos \ varphi && \\ y (\ varphi) & = & a \; (- \ sin (2 \ varphi) +2 \ sin \ varphi) & = & 2a (1- \ cos \ varphi) \ cdot \ sin \ varphi &. & \ end {array}}}$

(As fórmulas foram usadas. Consulte funções trigonométricas .) ${\ displaystyle e ^ {i \ varphi} = \ cos \ varphi + i \ sin \ varphi, \ (\ cos \ varphi) ^ {2} + (\ sin \ varphi) ^ {2} = 1, \ \ cos 2 \ varphi = (\ cos \ varphi) ^ {2} - (\ sin \ varphi) ^ {2}, \; \ sin 2 \ varphi = 2 \ sin \ varphi \ cos \ varphi}$

Propriedades métricas

Para o cardióide, conforme definido acima, as seguintes fórmulas são válidas:

• área ,${\ displaystyle A = 6 \ pi a ^ {2}}$
• comprimento do arco e${\ displaystyle L = 16a}$
• raio de curvatura ${\ displaystyle \ rho (\ varphi) = {\ tfrac {8} {3}} a \ sin {\ tfrac {\ varphi} {2}} \.}$

As provas dessa afirmação usam em ambos os casos a representação polar do cardióide. Para fórmulas adequadas, consulte o sistema de coordenadas polares (comprimento do arco) e o sistema de coordenadas polares (área)

prova da fórmula da área

${\ displaystyle A = 2 \ cdot {\ tfrac {1} {2}} \ int _ {0} ^ {\ pi} {(r (\ varphi)) ^ {2}} \; d \ varphi = \ int _ {0} ^ {\ pi} {4a ^ {2} (1- \ cos \ varphi) ^ {2}} \; d \ varphi = \ cdots = 4a ^ {2} \ cdot {\ tfrac {3} {2}} \ pi = 6 \ pi a ^ {2}}$ .

prova da fórmula do comprimento do arco

${\ displaystyle L = 2 \ int _ {0} ^ {\ pi} {\ sqrt {r (\ varphi) ^ {2} + (r '(\ varphi)) ^ {2}}} \; d \ varphi = \ cdots = 8a \ int _ {0} ^ {\ pi} {\ sqrt {{\ tfrac {1} {2}} (1- \ cos \ varphi)}} \; d \ varphi = 8a \ int _ {0} ^ {\ pi} \ sin ({\ tfrac {\ varphi} {2}}) d \ varphi = 16a}$ .

prova para o raio de curvatura

O raio de curvatura de uma curva em coordenadas polares com a equação é (s. Curvatura ) ${\ displaystyle \ rho}$${\ displaystyle r = r (\ varphi)}$

${\ displaystyle \ rho (\ varphi) = {\ frac {\ left [r (\ varphi) ^ {2} + {\ dot {r}} (\ varphi) ^ {2} \ right] ^ {3/2 }} {r (\ varphi) ^ {2} +2 {\ dot {r}} (\ varphi) ^ {2} -r (\ varphi) {\ ddot {r}} (\ varphi)}} \. }$

Para o cardióide, obtém-se ${\ displaystyle r (\ varphi) = 2a (1- \ cos \ varphi) = 4a \ sin ^ {2} {\ tfrac {\ varphi} {2}}}$

${\ displaystyle \ rho (\ varphi) = \ cdots = {\ frac {[16a ^ {2} \ sin ^ {2} {\ frac {\ varphi} {2}}] ^ {\ frac {3} {2 }}} {24a ^ {2} \ sin ^ {2} {\ frac {\ varphi} {2}}}} = {\ frac {8} {3}} a \ sin {\ frac {\ varphi} { 2}} \.}$

Propriedades

Acordes através da cúspide

• C1: acordes que passam pela cúspide do cardióide têm o mesmo comprimento .${\ displaystyle 4a}$
• C2: Os pontos médios das cordas através da cúspide encontram-se no perímetro do círculo gerador fixo (ver figura).

prova para C1

Os pontos estão em um acorde através da cúspide (= origem). Portanto ${\ displaystyle P: p (\ varphi), \; Q: p (\ varphi + \ pi)}$

${\ displaystyle | PQ | = r (\ varphi) + r (\ varphi + \ pi)}$

${\ displaystyle = 2a (1- \ cos \ varphi) + 2a (1- \ cos (\ varphi + \ pi)) = \ cdots = 4a}$ .

prova para C2

Para a prova, a representação no plano complexo (veja acima) é usada. Pelos pontos

${\ displaystyle P: \ p (\ varphi) = a \; (- e ^ {i2 \ varphi} + 2e ^ {i \ varphi} -1)}$

${\ displaystyle Q: \ p (\ varphi + \ pi) = a \; (- e ^ {i2 (\ varphi + \ pi)} + 2e ^ {i (\ varphi + \ pi)} - 1) = a \; (- e ^ {i2 \ varphi} -2e ^ {i \ varphi} -1)}$,

o ponto médio do acorde é ${\ displaystyle PQ}$

${\ displaystyle M: ​​\ {\ tfrac {1} {2}} (p (\ varphi) + p (\ varphi + \ pi)) = \ cdots = -a-ae ^ {i2 \ varphi}}$

que fica no perímetro do círculo com ponto médio e raio (veja a imagem). ${\ displaystyle -a}$${\ displaystyle a}$

Cardióide como curva inversa de uma parábola

• Um cardióide é a curva inversa de uma parábola com seu foco no centro de inversão (ver gráfico)

Para o exemplo mostrado no gráfico, os círculos do gerador têm raio . Portanto, o cardióide tem a representação polar ${\ displaystyle a = {\ tfrac {1} {2}}}$

${\ displaystyle r (\ varphi) = 1- \ cos \ varphi}$

e sua curva inversa

${\ displaystyle r (\ varphi) = {\ frac {1} {1- \ cos \ varphi}}}$,

que é uma parábola (v. parábola em coordenadas polares ) com a equação em coordenadas cartesianas. ${\ displaystyle x = {\ tfrac {1} {2}} (y ​​^ {2} -1)}$

Observação: Nem toda curva inversa de uma parábola é um cardióide. Por exemplo, se uma parábola é invertida em um círculo cujo centro está no vértice da parábola, o resultado é uma cissóide de Diocles .

Cardióide como envelope de um lápis de círculos

Na seção anterior, se invertermos adicionalmente as tangentes da parábola, obteremos um lápis de círculos pelo centro de inversão (origem). Uma consideração detalhada mostra: Os pontos médios dos círculos situam-se no perímetro do círculo gerador fixo. (O círculo gerador é a curva inversa da diretriz das parábolas.)

Essa propriedade dá origem ao seguinte método simples para desenhar um cardióide:

1) Escolha um círculo e um ponto em seu perímetro,${\ displaystyle c}$${\ displaystyle O}$

2) desenhar círculos contendo com centros em , e${\ displaystyle O}$${\ displaystyle c}$

3) desenhe o envelope desses círculos.

prova com condição de envelope

O envelope do lápis de curvas implicitamente dadas

${\ displaystyle F (x, y, t) = 0}$

com parâmetro consiste em tais pontos que são soluções do sistema não linear ${\ displaystyle t}$${\ displaystyle (x, y)}$

• ${\ displaystyle F (x, y, t) = 0, \ quad F_ {t} (x, y, t) = 0 \;}$( condição do envelope ).

( significa a derivada parcial para o parâmetro . ${\ displaystyle F_ {t}}$${\ displaystyle t}$

Deixe ser o círculo com ponto médio e raio . Então tem representação paramétrica . O lápis de círculos com centros no ponto de contenção pode ser representado implicitamente por ${\ displaystyle c}$${\ displaystyle (-1,0)}$${\ displaystyle 1}$${\ displaystyle c}$${\ displaystyle (-1+ \ cos t, \ sin t)}$${\ displaystyle c}$${\ displaystyle O = (0,0)}$

${\ displaystyle F (x, y, t) = (x + 1- \ cos t) ^ {2} + (y- \ sin t) ^ {2} - (2-2 \ cos t) = 0}$,

que é equivalente a

${\ displaystyle F (x, y, t) = x ^ {2} + y ^ {2} + 2x \; (1- \ cos t) -2y \; \ sin t = 0 \ ;.}$

A segunda condição do envelope é

${\ displaystyle F_ {t} (x, y, t) = 2x \; \ sin t-2y \; \ cos t = 0}$.

Verifica-se facilmente que os pontos do cardióide com a representação paramétrica

${\ displaystyle x (t) = 2 (1- \ cos t) \ cos t, \ quad y (t) = 2 (1- \ cos t) \ sin t}$

cumprir o sistema não linear acima. O parâmetro é idêntico ao parâmetro de ângulo do cardióide. ${\ displaystyle t}$

Cardióide como envelope de um lápis de linhas

Um método semelhante e simples para desenhar um cardióide usa um lápis de linhas . É devido a L. Cremona :

1. Desenhe um círculo, divida seu perímetro em partes iguais com pontos (imagem) e numere-os consecutivamente.${\ displaystyle 2N}$
2. Desenhe os acordes: . (ou seja: o segundo ponto é movido por velocidade dupla.)${\ displaystyle (1,2), (2,4), ...., (n, 2n), ...., (N, 2N), (N + 1,2), (N + 2, 4), ....,}$
3. O envelope desses acordes é cardióide.

prova

A consideração a seguir usa fórmulas trigonométricas para . Para manter os cálculos simples, a prova é dada para o cardióide com representação polar (ver seção Cardióides em diferentes posições ). ${\ displaystyle \ cos \ alpha + \ cos \ beta, \ \ sin \ alpha + \ sin \ beta, \ 1+ \ cos 2 \ alpha, \ \ cos 2 \ alpha, \ sin 2 \ alpha}$${\ displaystyle r = 2 (1 {\ color {red} +} \ cos \ varphi)}$

equação da tangente

do cardióide com representação polar : ${\ displaystyle r = 2 (1+ \ cos \ varphi)}$

Da representação paramétrica

${\ displaystyle x (\ varphi) = 2 (1+ \ cos \ varphi) \ cos \ varphi,}$

${\ displaystyle y (\ varphi) = 2 (1+ \ cos \ varphi) \ sin \ varphi}$

obtém-se o vetor normal . A equação da tangente é: ${\ displaystyle {\ vec {n}} = ({\ dot {y}}, - {\ dot {x}}) ^ {T}}$${\ displaystyle {\ dot {y}} (\ varphi) \ cdot (xx (\ varphi)) - {\ dot {x}} (\ varphi) \ cdot (yy (\ varphi)) = 0}$

${\ displaystyle (\ cos 2 \ varphi + \ cos \ varphi) \ cdot x \ + \ (\ sin 2 \ varphi + \ sin \ varphi) \ cdot y = 2 (1+ \ cos \ varphi) ^ {2} \.}$

Com a ajuda de fórmulas trigonométricas e subsequente divisão por , a equação da tangente pode ser reescrita como: ${\ displaystyle \ cos {\ tfrac {1} {2}} \ varphi}$

• ${\ displaystyle \ cos ({\ tfrac {3} {2}} \ varphi) \ cdot x + \ sin ({\ tfrac {3} {2}} \ varphi) \ cdot y = 4 (\ cos {\ tfrac { 1} {2}} \ varphi) ^ {3} \ quad 0 <\ varphi <2 \ pi, \ \ varphi \ neq \ pi.}$

equação do acorde

do círculo com ponto médio e raio : Para a equação da linha secante passando pelos dois pontos obtém-se: ${\ displaystyle (1,0)}$${\ displaystyle 3}$${\ displaystyle (1 + 3 \ cos \ theta, 3 \ sin \ theta), \ (1 + 3 \ cos {\ color {red} 2} \ theta, 3 \ sin {\ color {red} 2} \ theta ))}$

${\ displaystyle (\ sin \ theta - \ sin 2 \ theta) \ cdot x \ + \ (\ cos 2 \ theta - \ sin \ theta) \ cdot y = -2 \ cos \ theta - \ sin 2 \ theta \ .}$

Com a ajuda de fórmulas trigonométricas e a divisão subsequente pela equação da linha secante pode ser reescrita por: ${\ displaystyle \ sin {\ tfrac {1} {2}} \ theta}$

• ${\ displaystyle \ cos ({\ tfrac {3} {2}} \ theta) \ cdot x + \ sin ({\ tfrac {3} {2}} \ theta) \ cdot y = 4 (\ cos {\ tfrac { 1} {2}} \ theta) ^ {3} \ quad 0 <\ theta <2 \ pi.}$

Apesar de os dois ângulos terem significados diferentes (v. Imagem), um obtém para a mesma linha. Portanto, qualquer linha secante do círculo, definida acima, também é uma tangente do cardióide: ${\ displaystyle \ varphi, \ theta}$${\ displaystyle \ varphi = \ theta}$

• O cardióide é o envelope dos acordes de um círculo.

Observação:
A prova pode ser realizada com a ajuda das condições do envelope (ver seção anterior) de um lápis implícito de curvas:

${\ displaystyle F (x, y, t) = \ cos {\ tfrac {3} {2}} t \ cdot x \ + \ \ sin {\ tfrac {3} {2}} t \ cdot y-4 ( \ cos {\ tfrac {1} {2}} t) ^ {3} = 0 \}$ é o lápis das linhas secantes de um círculo (s. acima) e

${\ displaystyle F_ {t} (x, y, t) = - {\ tfrac {3} {2}} \ sin {\ tfrac {3} {2}} t \ cdot x \ + \ {\ tfrac {3 } {2}} \ cos {\ tfrac {3} {2}} t \ cdot y + 3 \ cos {\ tfrac {1} {2}} t \ sin t = 0 \.}$

Para o parâmetro fixo t, ambas as equações representam retas. Seu ponto de intersecção é

${\ displaystyle x (t) = 2 (1+ \ cos t) \ cos t, \ quad y (t) = 2 (1+ \ cos t) \ sin t}$,

que é um ponto do cardióide com equação polar ${\ displaystyle r = 2 (1+ \ cos t).}$

Cardióide como cáustico de um círculo

As considerações feitas na seção anterior fornecem uma prova de que a cáustica de um círculo com fonte de luz no perímetro do círculo é um cardióide.

• Se no plano houver uma fonte de luz em um ponto no perímetro de um círculo que está refletindo qualquer raio, então os raios refletidos dentro do círculo são tangentes de um cardióide.${\ displaystyle Z}$

prova

Como na seção anterior, o círculo pode ter ponto médio e raio . Sua representação paramétrica é ${\ displaystyle (1,0)}$${\ displaystyle 3}$

${\ displaystyle c (\ varphi) = (1 + 3 \ cos \ varphi, 3 \ sin \ varphi) \.}$

A tangente no ponto do círculo tem vetor normal . Portanto, o raio refletido tem o vetor normal (veja o gráfico) e contém o ponto . O raio refletido é parte da linha com a equação (consulte a seção anterior) ${\ displaystyle C: \ k (\ varphi)}$${\ displaystyle {\ vec {n}} _ {t} = (\ cos \ varphi, \ sin \ varphi) ^ {T}}$${\ displaystyle {\ vec {n}} _ {r} = (\ cos {\ color {red} {\ tfrac {3} {2}}} \ varphi, \ sin {\ color {red} {\ tfrac { 3} {2}}} \ varphi) ^ {T}}$${\ displaystyle C: \ (1 + 3 \ cos \ varphi, 3 \ sin \ varphi)}$

${\ displaystyle \ cos {\ tfrac {3} {2}} \ varphi \ cdot x \ + \ \ sin {\ tfrac {3} {2}} \ varphi \ cdot y = 4 (\ cos {\ tfrac {1 } {2}} \ varphi) ^ {3} \,}$

que é tangente do cardióide com equação polar

${\ displaystyle r = 2 (1+ \ cos \ varphi)}$

da seção anterior.

Observação: Para tais considerações, geralmente vários reflexos no círculo são negligenciados.

Cardióide como curva pedal de um círculo

A geração Cremona de um cardióide não deve ser confundida com a seguinte geração:

Let Ser um círculo e um ponto no perímetro deste círculo. O seguinte é verdadeiro: ${\ displaystyle k}$${\ displaystyle O}$

• As bases das perpendiculares do ponto nas tangentes do círculo são pontos de um cardióide.${\ displaystyle O}$${\ displaystyle k}$

Portanto, um cardióide é uma curva pedal especial de um círculo.

prova

Em um sistema de coordenadas cartesiano, o círculo pode ter ponto médio e raio . A tangente no ponto do círculo tem a equação ${\ displaystyle k}$${\ displaystyle (2a, 0)}$${\ displaystyle 2a}$${\ displaystyle (2a + 2a \ cos \ varphi, 2a \ sin \ varphi)}$

${\ displaystyle (x-2a) \ cdot \ cos \ varphi + y \ cdot \ sin \ varphi = 2a \.}$

O pé da perpendicular do ponto na tangente é o ponto com a ainda desconhecida distância até a origem . Inserir o ponto na equação dos rendimentos tangentes ${\ displaystyle O}$${\ displaystyle (r \ cos \ varphi, r \ sin \ varphi)}$${\ displaystyle r}$${\ displaystyle O}$

${\ displaystyle (r \ cos \ varphi -2a) \ cos \ varphi + r \ sin ^ {2} \ varphi = 2a \ quad \ rightarrow \ quad r = 2a (1+ \ cos \ varphi)}$

que é a equação polar de um cardióide.

Observação: Se o ponto não está no perímetro do círculo , obtém-se um limaçon de Pascal . ${\ displaystyle O}$${\ displaystyle k}$

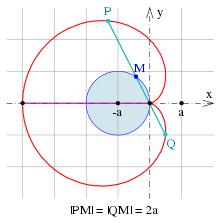
A evolução de um cardióide

A evolução de uma curva é o locus dos centros de curvatura. Em detalhe: Para uma curva com raio de curvatura o evolute tem a representação ${\ displaystyle {\ vec {x}} (s) = {\ vec {c}} (s)}$${\ displaystyle \ rho (s)}$

${\ displaystyle {\ vec {X}} (s) = {\ vec {c}} (s) + \ rho (s) {\ vec {n}} (s).}$

com a unidade devidamente orientada normal. ${\ displaystyle {\ vec {n}} (s)}$

Para um cardióide, obtém-se:

• A evolução de um cardióide é outro cardióide com um terço do tamanho (imagem s.).

prova

Para o cardióide com representação paramétrica

${\ displaystyle x (\ varphi) = 2a (1- \ cos \ varphi) \ cos \ varphi = 4a \ sin ^ {2} {\ tfrac {\ varphi} {2}} \ cos \ varphi \,}$

${\ displaystyle y (\ varphi) = 2a (1- \ cos \ varphi) \ sin \ varphi = 4a \ sin ^ {2} {\ tfrac {\ varphi} {2}} \ sin \ varphi}$

a unidade normal é

${\ displaystyle {\ vec {n}} (\ varphi) = (- \ sin {\ tfrac {3} {2}} \ varphi, \ cos {\ tfrac {3} {2}} \ varphi)}$

e o raio de curvatura

${\ displaystyle \ rho (\ varphi) = {\ tfrac {8} {3}} a \ sin {\ tfrac {\ varphi} {2}} \.}$

Portanto, as equações paramétricas da evolução são

${\ displaystyle X (\ varphi) = 4a \ sin ^ {2} {\ tfrac {\ varphi} {2}} \ cos \ varphi - {\ tfrac {8} {3}} a \ sin {\ tfrac {\ varphi} {2}} \ cdot \ sin {\ tfrac {3} {2}} \ varphi = \ cdots = {\ tfrac {4} {3}} a \ cos ^ {2} {\ tfrac {\ varphi} {2}} \ cos \ varphi - {\ tfrac {4} {3}} a \,}$

${\ displaystyle Y (\ varphi) = 4a \ sin ^ {2} {\ tfrac {\ varphi} {2}} \ sin \ varphi + {\ tfrac {8} {3}} a \ sin {\ tfrac {\ varphi} {2}} \ cdot \ cos {\ tfrac {3} {2}} \ varphi \ = \ cdots = {\ tfrac {4} {3}} a \ cos ^ {2} {\ tfrac {\ varphi } {2}} \ sin \ varphi \.}$

Essas equações descrevem um cardióide com um terço do tamanho, girado 180 graus e deslocado ao longo do eixo x em . ${\ displaystyle - {\ tfrac {4} {3}} a}$

(Foram usadas fórmulas trigonométricas: ) ${\ displaystyle \ sin {\ tfrac {3} {2}} \ varphi = \ sin {\ tfrac {\ varphi} {2}} \ cos \ varphi + \ cos {\ tfrac {\ varphi} {2}} \ sin \ varphi \, \ \ cos {\ tfrac {3} {2}} \ varphi = \ cdots, \ \ sin \ varphi = 2 \ sin {\ tfrac {\ varphi} {2}} \ cos {\ tfrac { \ varphi} {2}} \, \ \ cos \ varphi = \ cdots \.}$

Trajetórias ortogonais

Uma trajetória ortogonal de um lápis de curvas é uma curva que cruza qualquer curva do lápis ortogonalmente. Para cardióides, o seguinte é verdadeiro:

• As trajetórias ortogonais do pencil de cardioides com equações

${\ displaystyle r = 2a (1- \ cos \ varphi) \, \; a> 0 \, \}$

são os cardióides com equações

${\ displaystyle r = 2b (1+ \ cos \ varphi) \, \; b> 0 \.}$

(O segundo lápis pode ser considerado como reflexos no eixo y do primeiro. Veja o diagrama.)

Prova:
para uma curva dada em coordenadas polares por uma função, a seguinte conexão com as coordenadas cartesianas é válida: ${\ displaystyle r (\ varphi)}$

${\ displaystyle x (\ varphi) = r (\ varphi) \ cos \ varphi \, \ qquad}$ ${\ displaystyle y (\ varphi) = r (\ varphi) \ sin \ varphi \ qquad}$

e para os derivados

${\ displaystyle {\ frac {dx} {d \ varphi}} = r '(\ varphi) \ cos \ varphi -r (\ varphi) \ sin \ varphi \, \ qquad}$${\ displaystyle {\ frac {dy} {d \ varphi}} = r '(\ varphi) \ sin \ varphi + r (\ varphi) \ cos \ varphi \.}$

Dividir a segunda equação pela primeira produz a inclinação cartesiana da linha tangente à curva no ponto : ${\ displaystyle (r (\ varphi), \ varphi)}$

${\ displaystyle {\ frac {dy} {dx}} = {\ frac {r '(\ varphi) \ sin \ varphi + r (\ varphi) \ cos \ varphi} {r' (\ varphi) \ cos \ varphi -r (\ varphi) \ sin \ varphi}}.}$

Para os cardióides com as equações e respectivamente obtém-se: ${\ displaystyle r = 2a (1- \ cos \ varphi) \;}$${\ displaystyle r = 2b (1+ \ cos \ varphi) \}$

${\ displaystyle {\ frac {dy_ {a}} {dx}} = {\ frac {\ cos \ varphi - \ cos 2 \ varphi} {\ sin 2 \ varphi - \ sin \ varphi}} \ quad}$ e ${\ displaystyle \ quad {\ frac {dy_ {b}} {dx}} = - {\ frac {\ cos \ varphi + \ cos 2 \ varphi} {\ sin 2 \ varphi + \ sin \ varphi}} \. }$

(A inclinação de qualquer curva depende apenas de, e não dos parâmetros  !) Portanto ${\ displaystyle \ varphi}$${\ displaystyle a, b}$

${\ displaystyle {\ frac {dy_ {a}} {dx}} \ cdot {\ frac {dy_ {b}} {dx}} = \ cdots = - {\ frac {\ cos ^ {2} \ varphi - \ cos ^ {2} 2 \ varphi} {\ sin ^ {2} 2 \ varphi - \ sin ^ {2} \ varphi}} = - {\ frac {-1+ \ cos ^ {2} \ varphi + 1- \ cos ^ {2} 2 \ varphi} {\ sin ^ {2} 2 \ varphi - \ sin ^ {2} \ varphi}} = - 1 \.}$

Isso significa: Qualquer curva do primeiro lápis intersecta qualquer curva do segundo lápis ortogonalmente.

Em posições diferentes

A escolha de outras posições do cardióide no sistema de coordenadas resulta em diferentes equações. A imagem mostra as 4 posições mais comuns de um cardióide e suas equações polares.

Em análise complexa

Na análise complexa , a imagem de qualquer círculo através da origem sob o mapa é um cardióide. Uma aplicação desse resultado é que o limite do componente central do período-1 do conjunto de Mandelbrot é um cardióide dado pela equação${\ displaystyle z \ a z ^ {2}}$

${\ displaystyle c \, = \, {\ frac {1- \ left (e ^ {it} -1 \ right) ^ {2}} {4}}. \,}$

O conjunto de Mandelbrot contém um número infinito de cópias levemente distorcidas de si mesmo e o bulbo central de qualquer uma dessas cópias menores é um cardióide aproximado.

Cáusticos

Certos cáusticos podem assumir a forma de cardióides. A catacaustica de um círculo em relação a um ponto da circunferência é um cardióide. Além disso, a catacaustica de um cone em relação aos raios paralelos a uma linha geradora é uma superfície cuja seção transversal é cardióide. Isso pode ser visto, como na fotografia à direita, em um copo cônico parcialmente cheio de líquido quando uma luz brilha à distância e em um ângulo igual ao ângulo do cone. A forma da curva na parte inferior de uma xícara cilíndrica é a metade de um nefroide , que é bastante semelhante.

Veja também

• Limaçon
• Nephroid
• Deltóide
• Vara de Wittgenstein
• Microfone cardioide
• Lemniscate de Bernoulli
• Antena de loop
• Localizador de direção de rádio
• Localização de direção de rádio
• Antena yagi
• Giovanni Salvemini

Notas

Referências

• RC Yates (1952). "Cardióide". Um manual sobre curvas e suas propriedades . Ann Arbor, MI: JW Edwards. pp. 4 ff.
• Wells D (1991). O Dicionário Penguin de Geometria Curiosa e Interessante . Nova York: Penguin Books. pp.  24-25 . ISBN 0-14-011813-6.

links externos

• "Cardioid" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• O'Connor, John J .; Robertson, Edmund F. , "Cardioid" , arquivo MacTutor History of Mathematics , University of St Andrews
• Comendo cardióides farto no corte do nó
• Weisstein, Eric W. "Cardioid" . MathWorld .
• Weisstein, Eric W. "Epicycloid - 1-Cusped" . MathWorld .
• Weisstein, Eric W. "Heart Curve" . MathWorld .
• Xah Lee, Cardioid (1998) (Este site fornece uma série de construções alternativas) .
• Jan Wassenaar, Cardioid , (2005)