Teorema de Berry-Esseen - Berry–Esseen theorem

Na teoria da probabilidade , o teorema do limite central afirma que, sob certas circunstâncias, a distribuição de probabilidade da média escalonada de uma amostra aleatória converge para uma distribuição normal à medida que o tamanho da amostra aumenta para o infinito. Sob suposições mais fortes, o teorema de Berry-Esseen , ou desigualdade de Berry-Esseen , dá um resultado mais quantitativo, porque também especifica a taxa na qual essa convergência ocorre, dando um limite no erro máximo de aproximação entre a distribuição normal e a distribuição verdadeira da média da amostra em escala. A aproximação é medida pela distância de Kolmogorov – Smirnov . No caso de amostras independentes , a taxa de convergência é n ^−1/2 , onde n é o tamanho da amostra, e a constante é estimada em termos do terceiro momento normalizado absoluto .

Declaração do teorema

As declarações do teorema variam, já que ele foi descoberto independentemente por dois matemáticos , Andrew C. Berry (em 1941) e Carl-Gustav Esseen (1942), que então, junto com outros autores, o refinou repetidamente nas décadas subsequentes.

Summands distribuídos de forma idêntica

Uma versão, sacrificando um pouco a generalidade por uma questão de clareza, é a seguinte:

Existe uma constante positiva C tal que se X ₁ , X ₂ , ..., são iid variáveis ​​aleatórias com E ( X ₁ ) = 0, E ( X ₁ ² ) = σ ² > 0, e E (| X ₁ | ³ ) = ρ <∞, e se definirmos

${\ displaystyle Y_ {n} = {X_ {1} + X_ {2} + \ cdots + X_ {n} \ over n}}$

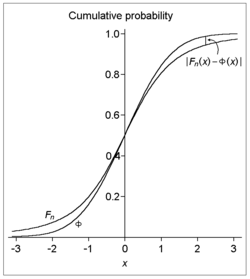
a média da amostra , com F _n a função de distribuição cumulativa de

${\ displaystyle {Y_ {n} {\ sqrt {n}} \ over {\ sigma}},}$

e Φ a função de distribuição cumulativa da distribuição normal padrão , então para todos os x e n ,

${\ displaystyle \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq {C \ rho \ over \ sigma ^ {3} {\ sqrt {n}}}. \ \ \ \ ( 1)}$

Ilustração da diferença nas funções de distribuição cumulativa aludidas no teorema.

Ou seja: dada uma sequência de variáveis ​​aleatórias independentes e distribuídas de forma idêntica , cada uma com média zero e variância positiva , se adicionalmente o terceiro momento absoluto for finito, então as funções de distribuição cumulativa da média da amostra padronizada e a distribuição normal padrão diferem (verticalmente, em um gráfico) por não mais do que o valor especificado. Observe que o erro de aproximação para todo n (e, portanto, a taxa limite de convergência para n indefinido suficientemente grande) é limitado pela ordem de n ^−1/2 .

Os valores calculados da constante C diminuíram acentuadamente ao longo dos anos, do valor original de 7,59 por Esseen (1942) , para 0,7882 por van Beek (1972) , depois 0,7655 por Shiganov (1986) , depois 0,7056 por Shevtsova (2007) , depois 0,7005 por Shevtsova (2008) , depois 0,5894 por Tyurin (2009) , depois 0,5129 por Korolev & Shevtsova (2010a) , depois 0,4785 por Tyurin (2010) . A revisão detalhada pode ser encontrada nos artigos Korolev & Shevtsova (2010a) e Korolev & Shevtsova (2010b) . A melhor estimativa em 2012, C  <0,4748, segue da desigualdade

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq {0,33554 (\ rho +0,415 \ sigma ^ {3} ) \ over \ sigma ^ {3} {\ sqrt {n}}},}$

devido a Shevtsova (2011) , uma vez que σ ³  ≤ ρ e 0,33554 · 1,415 <0,4748. No entanto, se ρ ≥ 1,286σ ³ , então a estimativa

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq {0,3328 (\ rho +0,429 \ sigma ^ {3} ) \ over \ sigma ^ {3} {\ sqrt {n}}},}$

o que também é comprovado em Shevtsova (2011) , fornece uma estimativa superior ainda mais restrita.

Esseen (1956) provou que a constante também satisfaz o limite inferior

${\ displaystyle C \ geq {\ frac {{\ sqrt {10}} + 3} {6 {\ sqrt {2 \ pi}}}} \ approx 0,40973 \ approx {\ frac {1} {\ sqrt {2 \ pi}}} + 0,01079.}$

Somandos distribuídos não identicamente

Sejam X ₁ , X ₂ , ..., variáveis ​​aleatórias independentes com E ( X _i ) = 0, E ( X _i ² ) = σ _i ² > 0, e E (| X _i | ³ ) = ρ _i < ∞. Além disso, vamos

${\ displaystyle S_ {n} = {X_ {1} + X_ {2} + \ cdots + X_ {n} \ over {\ sqrt {\ sigma _ {1} ^ {2} + \ sigma _ {2} ^ {2} + \ cdots + \ sigma _ {n} ^ {2}}}}}$

ser a n- ésima soma parcial normalizada . Denote F _n o cdf de S _n e Φ o cdf da distribuição normal padrão . Por uma questão de conveniência, denote

${\ displaystyle {\ vec {\ sigma}} = (\ sigma _ {1}, \ ldots, \ sigma _ {n}), \ {\ vec {\ rho}} = (\ rho _ {1}, \ ldots, \ rho _ {n}).}$

Em 1941, Andrew C. Berry provou que para todo n existe uma constante absoluta C ₁ tal que

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq C_ {1} \ cdot \ psi _ {1}, \ \ \ \ (2)}$

Onde

${\ displaystyle \ psi _ {1} = \ psi _ {1} {\ big (} {\ vec {\ sigma}}, {\ vec {\ rho}} {\ big)} = {\ Big (} { \ textstyle \ sum \ limits _ {i = 1} ^ {n} \ sigma _ {i} ^ {2}} {\ Big)} ^ {- 1/2} \ cdot \ max _ {1 \ leq i \ leq n} {\ frac {\ rho _ {i}} {\ sigma _ {i} ^ {2}}}.}$

Independentemente, em 1942, Carl-Gustav Esseen provou que para todo n existe uma constante absoluta C ₀ tal que

${\ displaystyle \ sup _ {x \ in \ mathbb {R}} \ left | F_ {n} (x) - \ Phi (x) \ right | \ leq C_ {0} \ cdot \ psi _ {0}, \ \ \ \ (3)}$

Onde

${\ displaystyle \ psi _ {0} = \ psi _ {0} {\ big (} {\ vec {\ sigma}}, {\ vec {\ rho}} {\ big)} = {\ Big (} { \ textstyle \ sum \ limits _ {i = 1} ^ {n} \ sigma _ {i} ^ {2}} {\ Big)} ^ {- 3/2} \ cdot \ sum \ limits _ {i = 1 } ^ {n} \ rho _ {i}.}$

É fácil ter certeza de que ψ ₀ ≤ψ ₁ . Devido a essa circunstância, a desigualdade (3) é convencionalmente chamada de desigualdade de Berry-Esseen, e a quantidade ψ ₀ é chamada de fração de Lyapunov de terceira ordem. Além disso, no caso em que a soma X ₁ , ..., X _n têm distribuições idênticas

${\ displaystyle \ psi _ {0} = \ psi _ {1} = {\ frac {\ rho _ {1}} {\ sigma _ {1} ^ {3} {\ sqrt {n}}}},}$

e, portanto, os limites indicados pelas desigualdades (1), (2) e (3) coincidem além da constante.

Em relação a C ₀ , obviamente, o limite inferior estabelecido por Esseen (1956) permanece válido:

${\ displaystyle C_ {0} \ geq {\ frac {{\ sqrt {10}} + 3} {6 {\ sqrt {2 \ pi}}}} = 0,4097 \ ldots.}$

Os limites superiores para C ₀ foram posteriormente reduzidos da estimativa original 7,59 devido a Esseen (1942) para (considerando apenas os resultados recentes) 0,9051 devido a Zolotarev (1967) , 0,7975 devido a van Beek (1972) , 0,7915 devido a Shiganov (1986 ) , 0,6379 e 0,5606 devido a Tyurin (2009) e Tyurin (2010) . Em 2011, a melhor estimativa é 0,5600 obtida por Shevtsova (2010) .

Versão multidimensional

Tal como acontece com o teorema do limite central multidimensional , existe uma versão multidimensional do teorema de Berry-Esseen.

Sejam vetores aleatórios de valores independentes, cada um tendo média zero. Escreva e presuma que é invertível. Let Ser a -dimensional Gaussian com a mesma média e matriz de covariância que . Então, para todos os conjuntos convexos , ${\ displaystyle X_ {1}, \ dots, X_ {n}}$${\ displaystyle \ mathbb {R} ^ {d}}$${\ displaystyle S = \ sum _ {i = 1} ^ {n} X_ {i}}$${\ displaystyle \ Sigma = \ operatorname {Cov} [S]}$${\ displaystyle Z \ sim \ operatorname {N} (0, \ Sigma)}$${\ displaystyle d}$${\ displaystyle S}$${\ displaystyle U \ subseteq \ mathbb {R} ^ {d}}$

${\ displaystyle {\ big |} \ Pr [S \ in U] - \ Pr [Z \ in U] \, {\ big |} \ leq Cd ^ {1/4} \ gamma}$ ,

onde é uma constante universal e (a terceira potência da norma L ² ). ${\ displaystyle C}$${\ displaystyle \ gamma = \ sum _ {i = 1} ^ {n} \ operatorname {E} {\ big [} \ | \ Sigma ^ {- 1/2} X_ {i} \ | _ {2} ^ {3} {\ big]}}$

A dependência de é considerada ótima, mas pode não ser. ${\ displaystyle d ^ {1/4}}$

Veja também

• Desigualdade de Chernoff
• Edgeworth series
• Lista de desigualdades
• Lista de teoremas matemáticos
• Desigualdade de concentração

Notas

Referências

links externos

• Gut, Allan e Holst Lars. Carl-Gustav Esseen , recuperado em 15 de março de 2004.
• "Desigualdade de Berry – Esseen" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]