Teorema da fatia de projeção - Projection-slice theorem

Teorema da fatia de Fourier

Em matemática , o teorema da projeco-fatia , teorema fatia central, ou de Fourier fatia teorema em duas dimensões estados que os resultados dos dois cálculos seguintes são iguais:

• Pegue uma função bidimensional f ( r ), projete (por exemplo, usando a transformação Radon ) em uma linha (unidimensional) e faça uma transformada de Fourier dessa projeção.
• Faça a mesma função, mas primeiro faça uma transformação de Fourier bidimensional e, em seguida, corte -a em sua origem, que é paralela à linha de projeção.

Em termos de operadora, se

• F ₁ e F ₂ são os operadores de transformada de Fourier uni e bidimensionais mencionados acima,
• P ₁ é o operador de projeção (que projeta uma função 2-D em uma linha 1-D),
• S ₁ é um operador de fatia (que extrai uma fatia central 1-D de uma função),

então

${\ displaystyle F_ {1} P_ {1} = S_ {1} F_ {2}.}$

Essa ideia pode ser estendida a dimensões superiores.

Este teorema é usado, por exemplo, na análise de tomografias computadorizadas médicas, onde uma "projeção" é uma imagem de raio-x de um órgão interno. As transformadas de Fourier dessas imagens são vistas como fatias através da transformada de Fourier da densidade tridimensional do órgão interno, e essas fatias podem ser interpoladas para construir uma transformada de Fourier completa dessa densidade. A transformada inversa de Fourier é então usada para recuperar a densidade tridimensional do objeto. Esta técnica foi derivada pela primeira vez por Ronald N. Bracewell em 1956 para um problema de radioastronomia.

O teorema da fatia de projeção em N dimensões

Em N dimensões, o teorema da fatia de projeção afirma que a transformada de Fourier da projeção de uma função N- dimensional f ( r ) em uma subvariedade linear m- dimensional é igual a uma fatia m- dimensional da transformada de Fourier N- dimensional de aquela função que consiste em uma subvariedade linear m- dimensional através da origem no espaço de Fourier que é paralela à subvariedade de projeção. Em termos de operadora:

${\ displaystyle F_ {m} P_ {m} = S_ {m} F_ {N}. \,}$

O teorema da fatia de Fourier generalizado

Além de generalizar para N dimensões, o teorema da fatia de projeção pode ser ainda mais generalizado com uma mudança arbitrária de base. Por conveniência de notação, consideramos a mudança de base a ser representada como B , uma matriz N- por- N invertível operando em vetores de coluna N- dimensionais. Então, o teorema generalizado da fatia de Fourier pode ser declarado como

${\ displaystyle F_ {m} P_ {m} B = S_ {m} {\ frac {B ^ {- T}} {| B ^ {- T} |}} F_ {N}}$

onde é a transposta do inverso da transformação da mudança de base. ${\ displaystyle B ^ {- T} = (B ^ {- 1}) ^ {T}}$

Prova em duas dimensões

Uma ilustração gráfica do teorema da fatia de projeção em duas dimensões. f ( r ) e F ( k ) são pares de transformadas de Fourier bidimensionais. A projeção de f ( r ) no eixo x é a integral de f ( r ) ao longo de linhas de visão paralelas ao eixo y e é rotulada como p ( x ). A fatia através de F ( k ) está no eixo k _x , que é paralelo ao eixo x e rotulado como s ( k _x ). O teorema da fatia de projeção afirma que p ( x ) es ( k _x ) são pares de transformadas de Fourier unidimensionais.

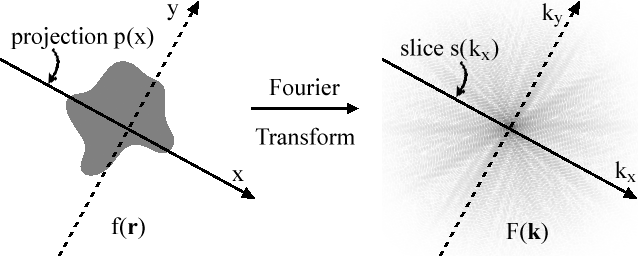
O teorema da fatia de projeção é facilmente comprovado para o caso de duas dimensões. Sem perda de generalidade, podemos considerar a linha de projeção como sendo o eixo x . Não há perda de generalidade porque se usarmos uma linha deslocada e girada, a lei ainda se aplica. Usar uma linha deslocada (em y) dá a mesma projeção e, portanto, os mesmos resultados da transformada de Fourier 1D. A função girada é o par de Fourier da transformada de Fourier girada, para a qual o teorema novamente é válido.

Se f ( x ,  y ) é uma função bidimensional, então a projeção de f ( x ,  y ) no eixo x é p ( x ) onde

${\ displaystyle p (x) = \ int _ {- \ infty} ^ {\ infty} f (x, y) \, dy.}$

A transformada de Fourier é ${\ displaystyle f (x, y)}$

${\ displaystyle F (k_ {x}, k_ {y}) = \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} f (x, y) \, e ^ {- 2 \ pi i (xk_ {x} + yk_ {y})} \, dxdy.}$

A fatia é então ${\ displaystyle s (k_ {x})}$

${\ displaystyle s (k_ {x}) = F (k_ {x}, 0) = \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} f (x , y) \, e ^ {- 2 \ pi ixk_ {x}} \, dxdy}$

${\ displaystyle = \ int _ {- \ infty} ^ {\ infty} \ left [\ int _ {- \ infty} ^ {\ infty} f (x, y) \, dy \ right] \, e ^ { -2 \ pi ixk_ {x}} dx}$

${\ displaystyle = \ int _ {- \ infty} ^ {\ infty} p (x) \, e ^ {- 2 \ pi ixk_ {x}} dx}$

que é apenas a transformada de Fourier de p ( x ). A prova para dimensões maiores é facilmente generalizada a partir do exemplo acima.

O ciclo FHA

Se a função bidimensional f ( r ) for circularmente simétrica, ela pode ser representada como f ( r ), onde r  = | r |. Neste caso, a projeção em qualquer linha de projeção será a transformada de Abel de f ( r ). A transformada de Fourier bidimensional de f ( r ) será uma função circularmente simétrica dada pela transformada de Hankel de ordem zero de f ( r ), que portanto também representará qualquer fatia através da origem. O teorema da fatia de projeção, então, afirma que a transformada de Fourier da projeção é igual à fatia ou

${\ displaystyle F_ {1} A_ {1} = H,}$

onde A ₁ representa o operador de transformada Abel, projetando uma função bidimensional circularmente simétrica em uma linha unidimensional, F ₁ representa o operador de transformada de Fourier 1-D e H representa o operador de transformada de Hankel de ordem zero.

Extensão para feixe de leque ou TC de feixe cônico

O teorema da fatia de projeção é adequado para a reconstrução de imagens de TC com projeções de feixe paralelas. Não se aplica diretamente a fanbeam ou conebeam CT. O teorema foi estendido para a reconstrução de imagem TC de feixe em leque e feixe de cone por Shuang-ren Zhao em 1995.

Veja também

• Transformada de radônio § Relacionamento com a transformada de Fourier

Referências

Leitura adicional

• Bracewell, Ronald N. (1990). "Transformadas Numéricas". Ciência . 248 (4956): 697–704. Bibcode : 1990Sci ... 248..697B . doi : 10.1126 / science.248.4956.697 . PMID   17812072 .
• Bracewell, Ronald N. (1956). "Faixa de integração em radioastronomia" . Aust. J. Phys . 9 (2): 198. bibcode : 1956AuJPh ... 9..198B . doi : 10.1071 / PH560198 .
• Gaskill, Jack D. (2005). Sistemas lineares, transformadas de Fourier e óptica . John Wiley & Sons, Nova York. ISBN   978-0-471-29288-3 .
• Ng, Ren (2005). "Fourier Slice Photography" (PDF) . Transações ACM em gráficos . 24 (3): 735–744. doi : 10.1145 / 1073204.1073256 .
• Zhao, Shuang-Ren; Halling, Horst (1995). "Reconstrução de projeções de feixe cônico com caminho de fonte livre por um método de Fourier generalizado". Proceedings of the 1995 International Meeting on Fully Tr-Dimensional Image Reconstruction in Radiology and Nuclear Medicine : 323-7.
• Garces, Daissy H .; Rhodes, William T .; Peña, Néstor (2011). "Teorema da projeção-fatia: Uma notação compacta". Jornal da Optical Society of America A . 28 (5): 766–769. Bibcode : 2011JOSAA..28..766G . doi : 10.1364 / JOSAA.28.000766 . PMID   21532686 .

links externos

• Teorema da fatia de Fourier (vídeo). Parte do curso "Tomografia Computadorizada e a Caixa de Ferramentas ASTRA". University of Antwerp . 10 de setembro de 2015.