Malha de subgrupos - Lattice of subgroups

Diagrama de Hasse da rede de subgrupos do grupo diédrico Dih 4 , com os subgrupos representados por seus gráficos de ciclo

Em matemática , a rede de subgrupos de um grupo é a rede cujos elementos são os subgrupos de , com a relação de ordem parcial sendo a inclusão do conjunto . Nesta rede, a união de dois subgrupos é o subgrupo gerado por sua união , e o encontro de dois subgrupos é sua interseção .

Exemplo

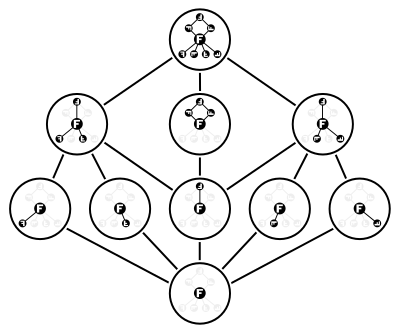
O grupo diédrico Dih 4 possui dez subgrupos, contando a si mesmo e o subgrupo trivial . Cinco dos oito elementos do grupo geram subgrupos de ordem dois, e os outros dois elementos de não identidade geram o mesmo subgrupo cíclico de ordem quatro. Além disso, existem dois subgrupos na forma Z 2 × Z 2 , gerados por pares de elementos de ordem dois. A rede formada por esses dez subgrupos é mostrada na ilustração.

Este exemplo também mostra que a rede de todos os subgrupos de um grupo não é uma rede modular em geral. Na verdade, esta rede particular contém o "pentágono" proibido N 5 como uma sub- rede .

Propriedades

Para qualquer subgrupo A , B e C de um grupo com A ≤ C ( A subgrupo de C ), então AB ∩ C = A (B ∩ C) ; a multiplicação aqui é o produto de subgrupos . Esta propriedade tem sido chamada de propriedade modular de grupos ( Aschbacher 2000 ) ou ( Dedekind ) lei modular ( Robinson 1996 , Cohn 2000 ). Visto que para dois subgrupos normais o produto é na verdade o menor subgrupo que contém os dois, os subgrupos normais formam uma rede modular .

O teorema da rede elétrica estabelece uma conexão de Galois entre a rede dos subgrupos de um grupo e a de seus quocientes.

O lema de Zassenhaus fornece um isomorfismo entre certas combinações de quocientes e produtos na rede de subgrupos.

Em geral, não há restrição quanto à forma da rede de subgrupos, no sentido de que toda rede é isomórfica a uma sub-rede da rede de subgrupo de algum grupo. Além disso, toda rede finita é isomórfica a uma sub-rede da rede de subgrupo de algum grupo finito ( Schmidt 1994 , p. 9).

Redes características

Os subgrupos com certas propriedades formam reticulados, mas outras propriedades não.

  • Os subgrupos normais sempre formam uma rede modular. Na verdade, a propriedade essencial que garante que a rede seja modular é que os subgrupos comutam entre si, ou seja, que são subgrupos quasinormais .
  • Os subgrupos normais nilpotentes formam uma rede, que é (parte) do conteúdo do teorema de Fitting .
  • Em geral, para qualquer classe de ajuste F , tanto os subgrupos F subnormais quanto os subgrupos F normais formam redes. Isso inclui o acima com F a classe de grupos nilpotentes, bem como outros exemplos, como F a classe de grupos solucionáveis . Uma classe de grupos é chamada de classe de ajuste se for fechada sob isomorfismo, subgrupos subnormais e produtos de subgrupos subnormais.
  • Os subgrupos centrais formam uma rede.

No entanto, nem subgrupos finitos nem subgrupos de torção formam uma rede: por exemplo, o produto livre é gerado por dois elementos de torção, mas é infinito e contém elementos de ordem infinita.

O fato de que os subgrupos normais formam uma rede modular é um caso particular de um resultado mais geral, ou seja, que em qualquer variedade de Maltsev (da qual os grupos são um exemplo), a rede de congruências é modular ( Kearnes & Kiss 2013 ).

Caracterizando grupos por seus subgrupos reticulados

As informações teóricas da rede sobre a rede de subgrupos podem às vezes ser usadas para inferir informações sobre o grupo original, uma ideia que remonta ao trabalho de Øystein Ore  ( 1937 , 1938 ). Por exemplo, como Ore provou, um grupo é localmente cíclico se e somente se sua rede de subgrupos for distributiva . Se, adicionalmente, a rede satisfizer a condição de cadeia ascendente , então o grupo é cíclico.

Os grupos cuja rede de subgrupos é uma rede complementada são chamados de grupos complementados ( Zacher 1953 ), e os grupos cuja rede de subgrupos são redes modulares são chamados grupos de Iwasawa ou grupos modulares ( Iwasawa 1941 ). As caracterizações teóricas da rede desse tipo também existem para grupos solucionáveis e grupos perfeitos ( Suzuki 1951 ).

Referências

  • Aschbacher, M. (2000). Teoria dos Grupos Finitos . Cambridge University Press. p. 6. ISBN   978-0-521-78675-1 .
  • Baer, ​​Reinhold (1939). “A importância do sistema de subgrupos para a estrutura do grupo”. American Journal of Mathematics . The Johns Hopkins University Press. 61 (1): 1–44. doi : 10.2307 / 2371383 . JSTOR   2371383 .
  • Cohn, Paul Moritz (2000). Álgebra clássica . Wiley. p. 248. ISBN   978-0-471-87731-8 .
  • Iwasawa, Kenkiti (1941), "Über die endlichen Gruppen und die Verbände ihrer Untergruppen", J. Fac. Sci. Criança levada. Univ. Tóquio. Sect. I. , 4 : 171–199, MR   0005721
  • Kearnes, Keith; Kiss, Emil W. (2013). The Shape of Congruence Lattices . American Mathematical Soc. p. 3. ISBN   978-0-8218-8323-5 .
  • Ore, Øystein (1937). "Estruturas e teoria dos grupos. I". Duke Mathematical Journal . 3 (2): 149–174. doi : 10.1215 / S0012-7094-37-00311-9 . MR   1545977 .
  • Ore, Øystein (1938). "Estruturas e teoria dos grupos. II". Duke Mathematical Journal . 4 (2): 247–269. doi : 10.1215 / S0012-7094-38-00419-3 . hdl : 10338.dmlcz / 100155 . MR   1546048 .
  • Robinson, Derek (1996). Um Curso de Teoria de Grupos . Springer Science & Business Media. p. 15. ISBN   978-0-387-94461-6 .
  • Rottlaender, Ada (1928). "Nachweis der Existenz nicht-isomorpher Gruppen von gleicher Situation der Untergruppen". Mathematische Zeitschrift . 28 (1): 641–653. doi : 10.1007 / BF01181188 . S2CID   120596994 .
  • Schmidt, Roland (1994). Redes de subgrupos de grupos . Exposições em matemática. 14 . Walter de Gruyter. ISBN   978-3-11-011213-9 . Resenha de Ralph Freese em Bull. AMS 33 (4): 487–492.
  • Suzuki, Michio (1951). "Na rede de subgrupos de grupos finitos" . Transactions of the American Mathematical Society . American Mathematical Society. 70 (2): 345–371. doi : 10.2307 / 1990375 . JSTOR   1990375 . CS1 maint: parâmetro desencorajado ( link )
  • Suzuki, Michio (1956). Estrutura de um grupo e a estrutura de sua rede de subgrupos . Berlim: Springer Verlag. CS1 maint: parâmetro desencorajado ( link )
  • Yakovlev, BV (1974). "Condições sob as quais uma rede é isomórfica a uma rede de subgrupos de um grupo". Álgebra e lógica . 13 (6): 400–412. doi : 10.1007 / BF01462952 . S2CID   119943975 .
  • Zacher, Giovanni (1953). "Caratterizzazione dei gruppi risolubili d'ordine finito complementati" . Rendiconti del Seminario Matematico della Università di Padova . 22 : 113–122. ISSN   0041-8994 . MR   0057878 .

links externos