Cascata fracionária - Fractional cascading

Na ciência da computação , o cascateamento fracionário é uma técnica para acelerar uma sequência de pesquisas binárias para o mesmo valor em uma sequência de estruturas de dados relacionadas. A primeira pesquisa binária na sequência leva um tempo logarítmico, como é padrão para pesquisas binárias, mas pesquisas sucessivas na sequência são mais rápidas. A versão original de cascata fracionária, introduzida em dois artigos de Chazelle e Guibas em 1986 ( Chazelle & Guibas 1986a ; Chazelle & Guibas 1986b ), combinou a ideia de cascata, originando-se nas estruturas de dados de busca de alcance de Lueker (1978) e Willard (1978 ) , com a ideia de amostragem fracionada, originada em Chazelle (1983) . Autores posteriores introduziram formas mais complexas de cascata fracionária que permitem que a estrutura de dados seja mantida conforme os dados mudam por uma sequência de eventos discretos de inserção e exclusão.

Exemplo

Como um exemplo simples de cascata fracionária, considere o seguinte problema. Recebemos como entrada uma coleção de k listas ordenadas L _i de números, de modo que o comprimento total Σ | L _i | de todas as listas é n , e deve processá-las para que possamos realizar pesquisas binárias para um valor de consulta q em cada uma das k listas. Por exemplo, com k = 4 e n = 17,

L ₁ = 24, 64, 65, 80, 93

L ₂ = 23, 25, 26

L ₃ = 13, 44, 62, 66

L ₄ = 11, 35, 46, 79, 81

A solução mais simples para esse problema de pesquisa é armazenar cada lista separadamente. Se fizermos isso, o requisito de espaço é O ( n ), mas o tempo para realizar uma consulta é O ( k log ( n / k )), pois devemos realizar uma pesquisa binária separada em cada uma das k listas. O pior caso para consultar essa estrutura ocorre quando cada uma das k listas tem o mesmo tamanho n / k , de modo que cada uma das k buscas binárias envolvidas em uma consulta leva tempo O (log ( n / k )).

Uma segunda solução permite consultas mais rápidas às custas de mais espaço: podemos mesclar todas as k listas em uma única grande lista L e associar a cada item x de L uma lista dos resultados da pesquisa de x em cada uma das listas menores L _i . Se descrevermos um elemento desta lista mesclada como x [ a , b , c , d ], onde x é o valor numérico e a , b , c e d são as posições (o primeiro número tem a posição 0) do próximo elemento pelo menos tão grande quanto x em cada uma das listas de entrada originais (ou a posição após o final da lista se tal elemento não existir), então teríamos

L = 11 [0,0,0,0], 13 [0,0,0,1], 23 [0,0,1,1], 24 [0,1,1,1], 25 [1, 1,1,1], 26 [1,2,1,1],

35 [1,3,1,1], 44 [1,3,1,2], 46 [1,3,2,2], 62 [1,3,2,3], 64 [1,3, 3,3], 65 [2,3,3,3],

66 [3,3,3,3], 79 [3,3,4,3], 80 [3,3,4,4], 81 [4,3,4,4], 93 [4,3, 4,5]

Esta solução combinada permite uma consulta no tempo O (log n  +  k ): simplesmente pesquise q em L e então relate os resultados armazenados no item x encontrado por esta pesquisa. Por exemplo, se q = 50, procurando por q em L encontra o item 62 [1,3,2,3], a partir do qual retornamos os resultados L ₁ [1] = 64, L ₂ [3] (um valor de bandeira indicando que q passou do final de L ₂ ), L ₃ [2] = 62 e L ₄ [3] = 79. No entanto, esta solução paga uma grande penalidade na complexidade do espaço: ela usa o espaço O ( kn ) como cada dos n itens em L devem armazenar uma lista de k resultados da pesquisa.

O cascateamento fracionário permite que esse mesmo problema de pesquisa seja resolvido com limites de tempo e espaço atendendo ao melhor dos dois mundos: tempo de consulta O (log n  +  k ) e espaço O ( n ). A solução em cascata fracionária é armazenar uma nova sequência de listas M _i . A lista final nesta sequência, M _k , é igual a L _k ; cada lista anterior M _i é formada pela fusão de L _i com cada segundo item de M _{i +1} . Com cada item x nesta lista mesclada, armazenamos dois números: a posição resultante da pesquisa de x em L _i e a posição resultante da pesquisa de x em M _{i +1} . Para os dados acima, isso nos daria as seguintes listas:

M ₁ = 24 [0, 1], 25 [1, 1], 35 [1, 3], 64 [1, 5], 65 [2, 5], 79 [3, 5], 80 [3, 6 ], 93 [4, 6]

M ₂ = 23 [0, 1], 25 [1, 1], 26 [2, 1], 35 [3, 1], 62 [3, 3], 79 [3, 5]

M ₃ = 13 [0, 1], 35 [1, 1], 44 [1, 2], 62 [2, 3], 66 [3, 3], 79 [4, 3]

M ₄ = 11 [0, 0], 35 [1, 0], 46 [2, 0], 79 [3, 0], 81 [4, 0]

Suponha que desejamos realizar uma consulta nesta estrutura, para q = 50. Primeiro fazemos uma pesquisa binária padrão para q em M ₁ , encontrando o valor 64 [1,5]. O "1" em 64 [1,5] nos diz que a busca por q em L ₁ deve retornar L ₁ [1] = 64. O "5" em 64 [1,5] nos diz que a localização aproximada de q em M ₂ é a posição 5. Mais precisamente, a busca binária por q em M ₂ retornaria o valor 79 [3,5] na posição 5 ou o valor 62 [3,3] um lugar antes. Comparando q com 62, e observando que ele é menor, determinamos que o resultado correto da pesquisa em M ₂ é 62 [3,3]. O primeiro "3" em 62 [3,3] nos diz que a pesquisa por q em L ₂ deve retornar L ₂ [3], um valor de sinalizador que significa que q passou do final da lista L ₂ . O segundo "3" em 62 [3,3] nos diz que a localização aproximada de q em M ₃ é a posição 3. Mais precisamente, a busca binária por q em M ₃ retornaria o valor 62 [2,3] na posição 3 ou o valor 44 [1,2] um lugar antes. Uma comparação de q com o menor valor 44 nos mostra que o resultado correto da pesquisa em M ₃ é 62 [2,3]. O "2" em 62 [2,3] nos diz que a pesquisa de q em L ₃ deve retornar L ₃ [2] = 62, e o "3" em 62 [2,3] nos diz que o resultado da pesquisa para q em M ₄ é M ₄ [3] = 79 [3,0] ou M ₄ [2] = 46 [2,0]; comparar q com 46 mostra que o resultado correto é 79 [3,0] e que o resultado da busca por q em L ₄ é L ₄ [3] = 79. Assim, encontramos q em cada uma de nossas quatro listas, por fazendo uma pesquisa binária na lista única M ₁ seguida por uma única comparação em cada uma das listas sucessivas.

De modo mais geral, para qualquer estrutura de dados desse tipo, realizamos uma consulta fazendo uma pesquisa binária por q em M ₁ e determinando a partir do valor resultante a posição de q em L ₁ . Então, para cada i > 1, usamos a posição conhecida de q em M _i para encontrar sua posição em M _{i +1} . O valor associado à posição de q em M _i aponta para uma posição em M _{i +1} que é o resultado correto da pesquisa binária para q em M _{i +1} ou está a um único passo desse resultado correto, portanto, de i para i  + 1 requer apenas uma única comparação. Assim, o tempo total para uma consulta é O (log n  +  k ).

Em nosso exemplo, as listas em cascata fracionada têm um total de 25 elementos, menos do que o dobro da entrada original. Em geral, o tamanho de M _i nesta estrutura de dados é no máximo

${\ displaystyle | L_ {i} | + {\ frac {1} {2}} | L_ {i + 1} | + {\ frac {1} {4}} | L_ {i + 2} | + \ cdots + {\ frac {1} {2 ^ {j}}} | L_ {i + j} | + \ cdots,}$

como pode ser facilmente comprovado por indução. Portanto, o tamanho total da estrutura de dados é no máximo

${\ displaystyle \ sum | M_ {i} | = \ sum | L_ {i} | \ left (1 + {\ frac {1} {2}} + {\ frac {1} {4}} + \ cdots \ direita) \ leq 2n = O (n),}$

como pode ser visto pelo reagrupamento das contribuições para o tamanho total provenientes da mesma lista de entrada L _i junto com as outras.

O problema geral

Em geral, a cascata fracionária começa com um gráfico de catálogo , um gráfico direcionado no qual cada vértice é rotulado com uma lista ordenada. Uma consulta nesta estrutura de dados consiste em um caminho no gráfico e um valor de consulta q ; a estrutura de dados deve determinar a posição de q em cada uma das listas ordenadas associadas aos vértices do caminho. Para o exemplo simples acima, o próprio gráfico do catálogo é um caminho, com apenas quatro nós. É possível que os vértices posteriores no caminho sejam determinados dinamicamente como parte de uma consulta, em resposta aos resultados encontrados pelas pesquisas nas partes anteriores do caminho.

Para lidar com consultas deste tipo, para um gráfico em que cada vértice tem no máximo d arestas de entrada e no máximo d arestas de saída para alguma constante d , as listas associadas a cada vértice são aumentadas por uma fração dos itens de cada vizinho de saída do vértice; a fração deve ser escolhida para ser menor que 1 / d , de modo que a quantidade total pela qual todas as listas são aumentadas permaneça linear no tamanho da entrada. Cada item em cada lista aumentada armazena com ele a posição daquele item na lista não aumentada armazenada no mesmo vértice e em cada uma das listas vizinhas de saída. No exemplo simples acima, d = 1, e aumentamos cada lista com 1/2 fração dos itens vizinhos.

Uma consulta nesta estrutura de dados consiste em uma pesquisa binária padrão na lista aumentada associada ao primeiro vértice do caminho da consulta, junto com pesquisas mais simples em cada vértice sucessivo do caminho. Se uma fração de 1 / r de itens é usada para aumentar as listas de cada item vizinho, então cada resultado de consulta sucessiva pode ser encontrado dentro de no máximo r etapas da posição armazenada no resultado da consulta do vértice do caminho anterior e, portanto, pode ser encontrado em tempo constante sem ter que realizar uma pesquisa binária completa.

Cascata fracionária dinâmica

Na cascata fracionária dinâmica , a lista armazenada em cada nó do gráfico do catálogo pode mudar dinamicamente, por uma sequência de atualizações em que os itens da lista são inseridos e excluídos. Isso causa várias dificuldades para a estrutura de dados.

Primeiro, quando um item é inserido ou excluído em um nó do gráfico do catálogo, ele deve ser colocado na lista aumentada associada a esse nó e pode fazer com que as alterações se propaguem para outros nós do gráfico do catálogo. Em vez de armazenar as listas aumentadas em matrizes, elas devem ser armazenadas como árvores de pesquisa binárias, de modo que essas mudanças possam ser tratadas de forma eficiente, ao mesmo tempo em que permitem pesquisas binárias das listas aumentadas.

Em segundo lugar, uma inserção ou exclusão pode causar uma mudança no subconjunto da lista associada a um nó que é passado para os nós vizinhos do grafo do catálogo. Não é mais viável, na configuração dinâmica, que esse subconjunto seja escolhido como os itens em cada d- ésima posição da lista, para alguns d , pois esse subconjunto mudaria drasticamente após cada atualização. Em vez disso, uma técnica intimamente relacionada às árvores B permite a seleção de uma fração de dados que é garantida como menor que 1 / d , com os itens selecionados garantidos a estar espaçados um número constante de posições na lista completa, e tal que uma inserção ou exclusão na lista aumentada associada a um nó faz com que as mudanças se propaguem para outros nós para uma fração das operações que é inferior a 1 / d . Dessa forma, a distribuição dos dados entre os nós satisfaz as propriedades necessárias para que o algoritmo de consulta seja rápido, garantindo que o número médio de operações da árvore de busca binária por inserção ou exclusão de dados seja constante.

Terceiro, e mais criticamente, a estrutura de dados em cascata fracionária estática mantém, para cada elemento x da lista aumentada em cada nó do gráfico do catálogo, o índice do resultado que seria obtido ao pesquisar por x entre os itens de entrada desse nó e entre as listas aumentadas armazenadas em nós vizinhos. No entanto, essa informação seria muito cara para manter no ambiente dinâmico. Inserir ou excluir um único valor x pode fazer com que os índices armazenados em um número ilimitado de outros valores sejam alterados. Em vez disso, as versões dinâmicas da cascata fracionária mantêm várias estruturas de dados para cada nó:

• Um mapeamento dos itens na lista aumentada do nó para pequenos números inteiros, de modo que a ordem das posições na lista aumentada seja equivalente à ordem de comparação dos números inteiros e um mapa reverso desses números inteiros de volta aos itens da lista. Uma técnica de Dietz (1982) permite que essa numeração seja mantida de forma eficiente.
• Uma estrutura de dados de pesquisa de inteiro, como uma árvore de van Emde Boas, para os números associados à lista de entrada do nó. Com esta estrutura, e o mapeamento de itens para inteiros, pode-se encontrar de forma eficiente para cada elemento x da lista aumentada, o item que seria encontrado na busca de x na lista de entrada.
• Para cada nó vizinho no gráfico do catálogo, um inteiro semelhante pesquisando na estrutura de dados os números associados ao subconjunto dos dados propagados do nó vizinho. Com esta estrutura, e o mapeamento de itens para inteiros, pode-se encontrar de forma eficiente para cada elemento x da lista aumentada, uma posição dentro de um número constante de passos da localização de x na lista aumentada associada ao nó vizinho.

Essas estruturas de dados permitem que a cascata fracionária dinâmica seja realizada em um momento de O (log  n ) por inserção ou exclusão, e uma sequência de k buscas binárias seguindo um caminho de comprimento k no gráfico de catálogo a ser realizada no tempo O (log  n  +  k  log log  n ).

Formulários

As camadas convexas de um conjunto de pontos, parte de uma estrutura de dados em cascata fracionada eficiente para relatórios de intervalo de meio plano.

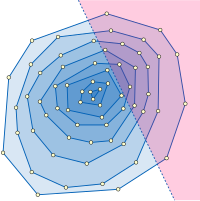
As aplicações típicas de cascata fracionária envolvem estruturas de dados de pesquisa de alcance em geometria computacional . Por exemplo, considere o problema do relatório de alcance de meio plano : isto é, interceptar um conjunto fixo de n pontos com um semiplano de consulta e listar todos os pontos na interseção. O problema é estruturar os pontos de forma que uma consulta desse tipo possa ser respondida de forma eficiente em termos do tamanho da interseção h . Uma estrutura que pode ser usada para esse propósito são as camadas convexas do conjunto de pontos de entrada, uma família de polígonos convexos aninhados que consiste no casco convexo do conjunto de pontos e nas camadas convexas construídas recursivamente dos pontos restantes. Dentro de uma única camada, os pontos dentro do meio-plano da consulta podem ser encontrados realizando uma pesquisa binária para a inclinação da linha de limite do meio-plano entre a sequência classificada de inclinações das bordas poligonais convexas, levando ao vértice do polígono que está dentro da metade da consulta -plano e mais distante de seu limite, e então procurando sequencialmente ao longo das bordas do polígono para encontrar todos os outros vértices dentro do semiplano da consulta. Todo o problema de relatório de intervalo de meio-plano pode ser resolvido repetindo este procedimento de pesquisa começando da camada mais externa e continuando para dentro até chegar a uma camada que está disjunta do meio-espaço de consulta. O cascateamento fracionário acelera as buscas binárias sucessivas entre as sequências de inclinações das arestas do polígono em cada camada, levando a uma estrutura de dados para este problema com espaço O ( n ) e tempo de consulta O (log  n  +  h ). A estrutura de dados pode ser construída no tempo O ( n  log  n ) por um algoritmo de Chazelle (1985) . Como em nosso exemplo, este aplicativo envolve pesquisas binárias em uma sequência linear de listas (a sequência aninhada das camadas convexas), portanto, o gráfico do catálogo é apenas um caminho.

Outra aplicação da cascata fracionária em estruturas de dados geométricas diz respeito à localização do ponto em uma subdivisão monótona, ou seja, uma partição do plano em polígonos de forma que qualquer linha vertical cruze qualquer polígono em no máximo dois pontos. Como Edelsbrunner, Guibas & Stolfi (1986) mostraram, esse problema pode ser resolvido encontrando uma sequência de caminhos poligonais que se estendem da esquerda para a direita através da subdivisão, e binário procurando pelo mais baixo desses caminhos que está acima do ponto de consulta. Testar se o ponto de consulta está acima ou abaixo de um dos caminhos pode ser resolvido como um problema de pesquisa binária, procurando a coordenada x dos pontos entre as coordenadas x dos vértices do caminho para determinar qual borda do caminho pode estar acima ou abaixo do ponto de consulta. Assim, cada consulta de localização de ponto pode ser resolvida como uma camada externa de busca binária entre os caminhos, cada etapa da qual realiza uma busca binária entre as coordenadas x dos vértices. O cascateamento fracionário pode ser usado para acelerar o tempo para as pesquisas binárias internas, reduzindo o tempo total por consulta para O (log  n ) usando uma estrutura de dados com espaço O ( n ). Nesta aplicação, o gráfico do catálogo é uma árvore que representa as possíveis sequências de pesquisa da pesquisa binária externa.

Além da geometria computacional, Lakshman & Stiliadis (1998) e Buddhikot, Suri & Waldvogel (1999) aplicam cascata fracionária no projeto de estruturas de dados para filtragem rápida de pacotes em roteadores de internet . Gao et al. (2004) usam cascata fracionária como um modelo para distribuição e recuperação de dados em redes de sensores .

Referências