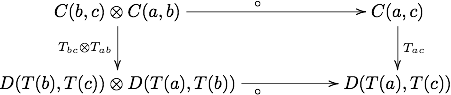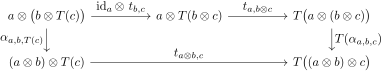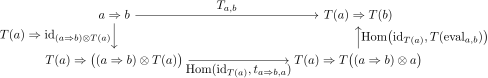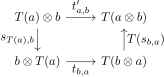Funtor enriquecido - Enriched functor
na teoria das categorias , um functor enriquecido é a generalização apropriada da noção de um functor para categorias enriquecidas . Os functores enriquecidos são então mapas entre categorias enriquecidas que respeitam a estrutura enriquecida.
Definição
Se C e D são M -categorias (isto é, categorias enriquecidas sobre a categoria monoidal M ), um functor M- enriquecido T : C → D é um mapa que atribui a cada objeto de C um objeto de D e para cada par de objetos a e b em C fornecem um morfismo em M
- T ab : C ( a , b ) → D ( T ( a ), T ( b ))
entre os hom-objetos de C e D (que são objetos em M ), satisfazendo versões enriquecidas dos axiomas de um functor, a saber, preservação da identidade e da composição.
Como os objetos hom não precisam ser colocados em uma categoria enriquecida, não se pode falar de um morfismo particular. Não há mais noção de um morfismo de identidade, nem de uma composição particular de dois morfismos. Em vez disso, os morfismos da unidade para um objeto hom devem ser pensados como a seleção de uma identidade, e os morfismos do produto monoidal devem ser pensados como composição. Os axiomas funcionais usuais são substituídos por diagramas comutativos correspondentes envolvendo esses morfismos. Em detalhes, temos que:
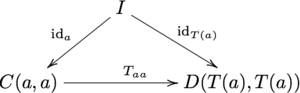
- Preservação de identidade: se I for o objeto de unidade de M e id a , id T ( a ) denotam as identidades de C e D, o diagrama
- comuta, o que equivale à equação T aa ∘ id a = id T ( a ) . Isso é análogo à regra F (id a ) = id F ( a ) para functores comuns.
- Preservação da composição: além disso, exige-se que o diagrama
- comuta, que é análoga à regra F ( f ∘ g ) = F ( f ) ∘ F ( g ) para functores ordinários.
Força
Functors enriquecidos são também chamados functors fortes (para não ser confundido com fortes functors monoidais ) e do mapa T ab é então chamado de força de T .
Pontos fortes são sempre transformações binatural do functor identidade a T .
Força Tensorial
Como toda categoria monoidal fechada M pode ser interpretada como uma categoria enriquecida sobre si mesma, um functor monoidal T : M → M junto com uma força T ab : M ( a , b ) → M ( T ( a ), T ( b )) conforme descrito na definição acima, pode ser visto como um functor enriquecido com M. Se T é um functor monoidal simétrico , há uma noção alternativa, mas equivalente, de uma força chamada força tensorial , dada por uma transformação binatural
- t ab : a ⊗ T ( b ) → T ( a ⊗ b )
de id ⊗ T a T satisfazendo as seguintes condições.
- Coerência da unidade esquerda: o diagrama a seguir comuta.
- Coerência de associatividade: o diagrama a seguir comuta.
Uma equivalência entre t ab e T ab pode ser encontrada fazendo com que os seguintes diagramas comutem.
Noções Alternativas
Como M é uma categoria monoidal simétrica , t ab dá origem a um comprimento tensorial
t ' ab : T ( a ) ⊗ b → T ( a ⊗ b )
satisfazendo a coerência de associatividade e a coerência de unidade certa :
fazendo o seguinte diagrama comutar:
Na programação funcional , uma força tensorial para um functor monoidal simétrica é geralmente administrado por uma transformação natural puro um : um → T ( um ) a partir do functor identidade de T . A correspondência entre as duas noções é ilustrada pelos seguintes diagramas comutativos: