Confluência (reescrita do resumo) - Confluence (abstract rewriting)

Na ciência da computação, a confluência é uma propriedade de sistemas de reescrita , descrevendo quais termos em tal sistema podem ser reescritos de mais de uma maneira, para produzir o mesmo resultado. Este artigo descreve as propriedades na configuração mais abstrata de um sistema de regravação abstrata .
Exemplos motivadores
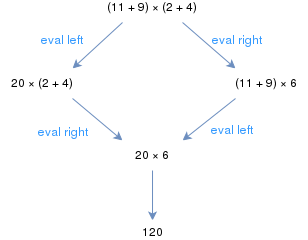
As regras usuais da aritmética elementar formam um sistema abstrato de reescrita. Por exemplo, a expressão (11 + 9) × (2 + 4) pode ser avaliada começando nos parênteses à esquerda ou à direita; entretanto, em ambos os casos, o mesmo resultado é obtido eventualmente. Se cada expressão aritmética for avaliada para o mesmo resultado, independentemente da estratégia de redução, o sistema de reescrita aritmética é considerado confluente com o solo. Os sistemas de reescrita aritmética podem ser confluentes ou apenas confluentes no solo, dependendo dos detalhes do sistema de reescrita.
Um segundo exemplo mais abstrato é obtido a partir da seguinte prova de que cada elemento do grupo é igual ao inverso de seu inverso:
| A1 | 1 ⋅ a | = a |
| A2 | a −1 ⋅ a | = 1 |
| A3 | ( a ⋅ b ) ⋅ c | = a ⋅ ( b ⋅ c ) |
| a −1 ⋅ ( a ⋅ b ) | ||
| = | ( a −1 ⋅ a ) ⋅ b | por A3 (r) |
| = | 1 ⋅ b | por A2 |
| = | b | por A1 |
| ( a −1 ) −1 ⋅ 1 | ||
| = | ( a −1 ) −1 ⋅ ( a −1 ⋅ a ) | por A2 (r) |
| = | uma | por R4 |
| ( a −1 ) −1 ⋅ b | ||
| = | ( a −1 ) −1 ⋅ ( a −1 ⋅ ( a ⋅ b )) | por R4 (r) |
| = | a ⋅ b | por R4 |
| a ⋅ 1 | ||
| = | ( a −1 ) −1 ⋅ 1 | por R10 (r) |
| = | uma | por R6 |
| ( a −1 ) −1 | ||
| = | ( a −1 ) −1 ⋅ 1 | por R11 (r) |
| = | uma | por R6 |
Esta prova começa com os axiomas de grupo A1-A3, e estabelece cinco proposições R4, R6, R10, R11 e R12, cada uma delas usando alguns dos anteriores, e R12 sendo o teorema principal. Algumas das provas requerem etapas não óbvias, ou mesmo criativas, como aplicar o axioma A2 ao contrário, reescrevendo assim "1" para " a −1 ⋅ a" na primeira etapa da prova de R6. Uma das motivações históricas para desenvolver a teoria da reescrita de termos foi evitar a necessidade dessas etapas, que são difíceis de encontrar por um ser humano inexperiente, muito menos por um programa de computador.
Se um sistema de reescrita de termo for confluente e encerrado , existe um método direto para provar a igualdade entre duas expressões (também conhecidas como termos ) s e t : começando com s , aplique igualdades da esquerda para a direita o maior tempo possível, eventualmente obtendo um termo s ′ . Obtenha de t um termo t ′ de maneira semelhante. Se ambos os termos s ′ e t ′ concordam literalmente, então s e t são (não surpreendentemente) provados iguais. Mais importante, se eles discordarem, s e t não podem ser iguais. Ou seja, quaisquer dois termos s e t que possam ser provados iguais, podem ser por esse método.
O sucesso desse método não depende de uma determinada ordem sofisticada na qual aplicar regras de reescrita, pois a confluência garante que qualquer sequência de aplicações de regra acabará levando ao mesmo resultado (enquanto a propriedade de terminação garante que qualquer sequência acabará por chegar ao fim em absoluto). Portanto, se um sistema confluente e final de reescrita de termos pode ser fornecido para alguma teoria equacional, nem um toque de criatividade é necessário para realizar provas de igualdade de termos; essa tarefa, portanto, torna-se acessível a programas de computador. Abordagens modernas lidar com mais gerais sistemas de reescrita abstratas em vez de prazo sistemas de reescrita; os últimos são um caso especial do primeiro.
Caso geral e teoria
Um sistema de reescrita pode ser expresso como um gráfico direcionado no qual os nós representam expressões e as arestas representam reescritas. Assim, por exemplo, se a expressão a pode ser reescrita em b , então dizemos que b é um redutor de a (alternativamente, a reduz para b , ou a é uma expansão de b ). Isso é representado usando notação de seta; a → b indica que a se reduz a b . Intuitivamente, isso significa que o gráfico correspondente tem uma aresta direcionada de a para b .
Se houver um caminho entre dois nós do gráfico c e d , ele forma uma sequência de redução . Então, por exemplo, se c → c ′ → c ′ ′ → ... → d ′ → d , então podemos escrever c d , indicando a existência de uma seqüência de redução de c para d . Formalmente,é o fechamento reflexivo-transitivo de →. Usando o exemplo do parágrafo anterior, temos (11 + 9) × (2 + 4) → 20 × (2 + 4) e 20 × (2 + 4) → 20 × 6, então (11 + 9) × ( 2 + 4) 20 × 6.
Com isso estabelecido, a confluência pode ser definida como segue. a ∈ S é considerado confluente se para todos os pares b , c ∈ S tal que a b e a c , existe a d ∈ S com b d e c d (denotado ). Se todo a ∈ S é confluente, dizemos que → é confluente. Essa propriedade também é às vezes chamada de propriedade diamante , após a forma do diagrama mostrado à direita. Alguns autores reservam o termo propriedade do diamante para uma variante do diagrama com reduções simples em todos os lugares; isto é, sempre que um → b e um → c , deve existir um d de tal modo que b → d e c → d . A variante de redução única é estritamente mais forte do que a de redução múltipla.
Confluência de solo
Um sistema é fundamentalmente confluente se todos os termos básicos forem confluentes, ou seja, todos os termos sem variáveis.
Confluência local
Um elemento de um ∈ S é dito ser localmente (ou fracamente) confluente se para todos b , c ∈ S com um → b e um → c existe d ∈ S com b d e c d . Se todo a ∈ S é localmente confluente, então → é chamado localmente (ou fracamente) confluente, ou tendo a propriedade Church-Rosser fraca . Isto é diferente de confluência em que b e c deve ser reduzido a partir de um em um passo. Em analogia com isso, a confluência às vezes é chamada de confluência global .
A relação , introduzido como uma notação para sequências de redução, pode ser visto como um sistema de reescrita em seu próprio direito, cuja relação é o fechamento reflexivo-transitivo de → . Uma vez que uma sequência de sequências de redução é novamente uma sequência de redução (ou, de forma equivalente, uma vez que formar o fechamento reflexivo-transitivo é idempotente ), = . Conclui-se que → é confluente se e somente se é localmente confluente.
Um sistema de reescrita pode ser localmente confluente sem ser (globalmente) confluente. Os exemplos são mostrados nas figuras 3 e 4. No entanto, o lema de Newman afirma que se um sistema de reescrita localmente confluente não tem sequências de redução infinitas (em cujo caso é dito que está terminando ou normalizando fortemente ), então é globalmente confluente.
Propriedade Church-Rosser
Diz-se que um sistema de reescrita possui a propriedade Church-Rosser se e somente se implica para todos os objetos x , y . Alonzo Church e J. Barkley Rosser provaram em 1936 que o cálculo lambda tem essa propriedade; daí o nome da propriedade. (O fato de que o cálculo lambda tem essa propriedade também é conhecido como teorema de Church-Rosser .) Em um sistema de reescrita com a propriedade de Church-Rosser, a palavra problema pode ser reduzida à procura de um sucessor comum. Em um sistema Church-Rosser, um objeto tem no máximo uma forma normal; essa é a forma normal de um objeto é único se existir, mas pode muito bem não existir. No cálculo lambda, por exemplo, a expressão (λx.xx) (λx.xx) não tem uma forma normal porque existe uma sequência infinita de reduções beta (λx.xx) (λx.xx) → (λx.xx) ( λx.xx) → ...
Um sistema de reescrita possui a propriedade Church-Rosser se e somente se for confluente. Por causa dessa equivalência, uma pequena variação nas definições é encontrada na literatura. Por exemplo, em Terese a propriedade e a confluência de Church-Rosser são definidas como sinônimos e idênticos à definição de confluência apresentada aqui; Church-Rosser, conforme definido aqui, permanece sem nome, mas é fornecido como uma propriedade equivalente; este afastamento de outros textos é deliberado.
Semi-confluência
A definição de confluência local difere daquela de confluência global em que apenas os elementos alcançados a partir de um determinado elemento em uma única etapa de reescrita são considerados. Ao considerar um elemento alcançado em uma única etapa e outro elemento alcançado por uma sequência arbitrária, chegamos ao conceito intermediário de semi-confluência: a ∈ S é dito semi-confluente se para todo b , c ∈ S com a → b e a c existe d ∈ S com b d e c d ; se todo a ∈ S é semi-confluente, dizemos que → é semi-confluente.
Um elemento semiconfluente não precisa ser confluente, mas um sistema de reescrita semiconfluente é necessariamente confluente e um sistema confluente é trivialmente semiconfluente.
Forte confluência
A forte confluência é outra variação da confluência local que nos permite concluir que um sistema de reescrita é globalmente confluente. Diz-se que um elemento a ∈ S é fortemente confluente se para todo b , c ∈ S com a → b e a → c existe d ∈ S com b d e c → d ou c = d ; se todo a ∈ S é fortemente confluente, dizemos que → é fortemente confluente.
Um elemento confluente não precisa ser fortemente confluente, mas um sistema de reescrita fortemente confluente é necessariamente confluente.
Exemplos de sistemas confluentes
- Redução de módulo de polinômios um ideal é um sistema de reescrita confluente, desde que se trabalhe com uma base de Gröbner .
- O teorema de Matsumoto segue da confluência das relações da trança.
- A redução β de termos λ é confluente pelo teorema de Church-Rosser .
Veja também
Notas
Referências
- Term Rewriting Systems , Terese, Cambridge Tracts in Theoretical Computer Science, 2003.
- Reescrita de termos e tudo isso , Franz Baader e Tobias Nipkow , Cambridge University Press, 1998