Pacote de ondas - Wave packet

Um pacote de ondas sem dispersão (parte real ou imaginária)

Um pacote de ondas com dispersão

Na física, um pacote de ondas (ou trem de ondas ) é uma pequena "explosão" ou " envelope " de ação de onda localizada que viaja como uma unidade. Um pacote de ondas pode ser analisado ou sintetizado a partir de um conjunto infinito de ondas sinusoidais componentes de diferentes números de onda , com fases e amplitudes tais que interferem construtivamente apenas em uma pequena região do espaço e destrutivamente em outro lugar. Cada função de onda componente e, portanto, o pacote de onda, são soluções de uma equação de onda . Dependendo da equação da onda, o perfil do pacote de ondas pode permanecer constante (sem dispersão , veja a figura) ou pode mudar (dispersão) durante a propagação.

A mecânica quântica atribui um significado especial ao pacote de ondas; é interpretado como uma amplitude de probabilidade , sua norma ao quadrado descrevendo a densidade de probabilidade de que uma partícula ou partículas em um determinado estado serão medidas para ter uma determinada posição ou momento. A equação de onda é, neste caso, a equação de Schrödinger , e através de sua aplicação é possível deduzir a evolução temporal de um sistema de mecânica quântica, semelhante ao processo do formalismo hamiltoniano na mecânica clássica . O caráter dispersivo das soluções da equação de Schrödinger desempenhou um papel importante na rejeição da interpretação original de Schrödinger e na aceitação da regra de Born .

Na representação de coordenadas da onda (como o sistema de coordenadas cartesiano ), a posição da probabilidade localizada do objeto físico é especificada pela posição da solução do pacote. Além disso, quanto mais estreito for o pacote de onda espacial e, portanto, melhor localizada a posição do pacote de onda, maior será a propagação no momento da onda. Este trade-off entre spread na posição e spread no momento é uma característica do princípio da incerteza de Heisenberg e será ilustrado abaixo.

Contexto histórico

No início dos anos 1900, tornou-se evidente que a mecânica clássica apresentava algumas falhas importantes. Isaac Newton propôs originalmente a ideia de que a luz vinha em pacotes discretos, que ele chamou de corpúsculos , mas o comportamento ondulatório de muitos fenômenos de luz rapidamente levou os cientistas a favorecer uma descrição ondulatória do eletromagnetismo . Foi só na década de 1930 que a natureza das partículas da luz realmente começou a ser amplamente aceita na física. O desenvolvimento da mecânica quântica - e seu sucesso em explicar resultados experimentais confusos - estava na raiz dessa aceitação. Assim, um dos conceitos básicos na formulação da mecânica quântica é o da luz que vem em feixes discretos chamados fótons . A energia de um fóton é uma função de sua frequência,

${\ displaystyle E = h \ nu.}$

A energia do fóton é igual à constante de Planck , h , multiplicada por sua frequência, ν . Isso resolveu um problema da física clássica, chamado de catástrofe ultravioleta .

As ideias da mecânica quântica continuaram a ser desenvolvidas ao longo do século XX. A imagem que foi desenvolvida era de um mundo particulado, com todos os fenômenos e matéria feitos de e interagindo com partículas discretas; no entanto, essas partículas foram descritas por uma onda de probabilidade. As interações, localizações e toda a física seriam reduzidas aos cálculos dessas amplitudes de probabilidade.

A natureza semelhante a uma partícula do mundo foi confirmada por experimentos ao longo de um século, enquanto os fenômenos semelhantes a ondas poderiam ser caracterizados como consequências do aspecto do pacote de ondas das partículas quânticas (ver dualidade onda-partícula ). De acordo com o princípio da complementaridade , as características de onda e de partícula nunca se manifestam ao mesmo tempo, ou seja, no mesmo experimento; veja, no entanto, o experimento Afshar e a discussão animada em torno dele.

Comportamentos básicos

A densidade de probabilidade de espaço de posição de um estado inicialmente gaussiano preso em um poço de potencial infinito experimentando tunelamento quântico periódico em uma parede potencial centrada.

Não dispersivo

Como um exemplo de propagação sem dispersão , considere soluções de onda para a seguinte equação de onda da física clássica

${\ displaystyle {\ partial ^ {2} u \ over \ partial t ^ {2}} = c ^ {2} \, \ nabla ^ {2} u,}$

onde c é a velocidade de propagação da onda em um determinado meio.

Usando a convenção de tempo da física, exp (- iωt ) , a equação de onda tem soluções de ondas planas

${\ displaystyle u (\ mathbf {x}, t) = e ^ {i {(\ mathbf {k \ cdot x}} - \ omega t)},}$

Onde

${\ displaystyle \ omega ^ {2} = | \ mathbf {k} | ^ {2} c ^ {2},}$ e ${\ displaystyle | \ mathbf {k} | ^ {2} = k_ {x} ^ {2} + k_ {y} ^ {2} + k_ {z} ^ {2}.}$

Esta relação entre ω e k deve ser válida para que a onda plana seja uma solução para a equação da onda. É chamada de relação de dispersão .

Para simplificar, considere apenas as ondas que se propagam em uma dimensão (a extensão para três dimensões é direta). Então, a solução geral é

${\ displaystyle u (x, t) = Ae ^ {i (kx- \ omega t)} + Be ^ {- i (kx + \ omega t)},}$

em que podemos tomar ω = kc . O primeiro termo representa uma onda que se propaga na direção x positiva, uma vez que é uma função de x - ct apenas; o segundo termo, sendo uma função de x + ct , representa uma onda que se propaga na direção x negativa .

Um pacote de ondas é um distúrbio localizado que resulta da soma de muitas formas de onda diferentes . Se o pacote estiver fortemente localizado, mais frequências são necessárias para permitir a sobreposição construtiva na região de localização e sobreposição destrutiva fora da região. A partir das soluções básicas em uma dimensão, uma forma geral de um pacote de ondas pode ser expressa como

${\ displaystyle u (x, t) = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {- \ infty} ^ {\, \ infty} A (k) ~ e ^ {i (kx- \ omega (k) t)} \, dk.}$

Como no caso da onda plana, o pacote de ondas viaja para a direita para ω (k) = kc , uma vez que u (x, t) = F (x - ct) , e para a esquerda para ω (k) = −kc , uma vez que u (x, t) = F (x + ct) .

O fator 1 ⁄ √ 2π vem das convenções da transformada de Fourier . A amplitude A (k) contém os coeficientes da superposição linear das soluções de onda plana. Esses coeficientes podem, por sua vez, ser expressos como uma função de u (x, t) avaliada em t = 0 invertendo a relação da transformada de Fourier acima:

${\ displaystyle A (k) = {\ frac {1} {\ sqrt {2 \ pi}}} \ int _ {- \ infty} ^ {\, \ infty} u (x, 0) ~ e ^ {- ikx} \, dx.}$

Por exemplo, escolher

${\ displaystyle u (x, 0) = e ^ {- x ^ {2} + ik_ {0} x},}$

nós obtemos

${\ displaystyle A (k) = {\ frac {1} {\ sqrt {2}}} e ^ {- {\ frac {(k-k_ {0}) ^ {2}} {4}}},}$

e finalmente

${\ displaystyle {\ begin {alinhados} u (x, t) & = e ^ {- (x-ct) ^ {2} + ik_ {0} (x-ct)} \\ & = e ^ {- ( x-ct) ^ {2}} \ left [\ cos \ left (2 \ pi {\ frac {x-ct} {\ lambda}} \ right) + i \ sin \ left (2 \ pi {\ frac { x-ct} {\ lambda}} \ right) \ right]. \ end {alinhado}}}$

A propagação não dispersiva da parte real ou imaginária deste pacote de ondas é apresentada na animação acima.

Dispersivo

A densidade de probabilidade do espaço de posição de um estado inicialmente gaussiano movendo-se em uma dimensão em momento mínimo incerto e constante no espaço livre.

Em contraste, como um exemplo de propagação agora com dispersão , considere, em vez disso, soluções para a equação de Schrödinger (com m e ħ iguais a um),

${\ displaystyle i {\ partial \ psi \ over \ partial t} = - {\ frac {1} {2}} {\ nabla ^ {2} \ psi},}$

produzindo a relação de dispersão

${\ displaystyle \ omega = {\ frac {1} {2}} | \ mathbf {k} | ^ {2}.}$

Mais uma vez, restringindo a atenção a uma dimensão, a solução para a equação de Schrödinger que satisfaz a condição inicial , representando um pacote de ondas localizado no espaço na origem, é visto como ${\ displaystyle ~ \ psi (x, 0) = {\ sqrt [{4}] {2 / \ pi}} \ exp ({- x ^ {2} + ik_ {0} x})}$

${\ displaystyle {\ begin {alinhados} \ psi (x, t) & = {\ frac {\ sqrt [{4}] {2 / \ pi}} {\ sqrt {1 + 2it}}} e ^ {- {\ frac {1} {4}} k_ {0} ^ {2}} ~ e ^ {- {\ frac {1} {1 + 2it}} \ left (x - {\ frac {ik_ {0}} {2}} \ right) ^ {2}} \\ & = {\ frac {\ sqrt [{4}] {2 / \ pi}} {\ sqrt {1 + 2it}}} e ^ {- {\ frac {1} {1 + 4t ^ {2}}} (x-k_ {0} t) ^ {2}} ~ e ^ {i {\ frac {1} {1 + 4t ^ {2}}} \ esquerda ((k_ {0} + 2tx) x - {\ frac {1} {2}} tk_ {0} ^ {2} \ direita)} ~. \ end {alinhado}}}$

Uma impressão do comportamento dispersivo deste pacote de ondas é obtida observando a densidade de probabilidade:

${\ displaystyle | \ psi (x, t) | ^ {2} = {\ frac {\ sqrt {2 / \ pi}} {\ sqrt {1 + 4t ^ {2}}}} ~ e ^ {- { \ frac {2 (x-k_ {0} t) ^ {2}} {1 + 4t ^ {2}}}} ~.}$

É evidente que este pacote de onda dispersiva, enquanto se move com velocidade de grupo constante k _o , está se deslocando rapidamente: tem uma largura que aumenta com o tempo como √ 1 + 4 t ² → 2 t , então eventualmente ele se difunde para uma região ilimitada do espaço .

O perfil de momento A (k) permanece invariante. A probabilidade atual é

${\ displaystyle j = \ rho v = {\ frac {1} {2i}} (\ psi ^ {*} \ nabla \ psi - \ psi \ nabla \ psi ^ {*}) = \ rho \ left (k_ { 0} + {\ frac {4t (x-k_ {0} t)} {1 + 4t ^ {2}}} \ right).}$

Pacotes de ondas gaussianas em mecânica quântica

Superposição de ondas planas 1D (azul) que se somam para formar um pacote de ondas gaussianas quânticas (vermelho) que se propaga para a direita enquanto se espalha. Os pontos azuis seguem a velocidade de fase de cada onda plana, enquanto a linha vermelha segue a velocidade do grupo central.

Posicione a densidade de probabilidade de espaço de um estado inicialmente Gaussiano preso em um poço de potencial infinito experimentando um túnel quântico periódico em uma parede de potencial centrada.

Pacote de ondas gaussianas 1D, mostrado no plano complexo, para a = 2 ek = 4

O pacote de ondas gaussianas dispersivas acima, não normalizado e apenas centrado na origem, em vez disso, em t = 0, agora pode ser escrito em 3D, agora em unidades padrão:

${\ displaystyle \ psi (\ mathbf {r}, 0) = e ^ {- \ mathbf {r} \ cdot \ mathbf {r} / 2a},}$

onde a é um número real positivo, o quadrado da largura do pacote de ondas ,

${\ displaystyle a = 2 \ langle \ mathbf {r} \ cdot \ mathbf {r} \ rangle / 3 \ langle 1 \ rangle = 2 (\ Delta x) ^ {2}.}$

A transformada de Fourier também é gaussiana em termos do número de onda, t = 0, o vetor k , (com largura inversa,

${\ displaystyle 1 / a = 2 \ langle \ mathbf {k} \ cdot \ mathbf {k} \ rangle / 3 \ langle 1 \ rangle = 2 (\ Delta p_ {x} / \ hbar) ^ {2},}$

de modo a

${\ displaystyle \ Delta x \ Delta p_ {x} = \ hbar / 2,}$

ou seja, satura a relação de incerteza ),

${\ displaystyle \ psi (\ mathbf {k}, 0) = (2 \ pi a) ^ {3/2} e ^ {- a \ mathbf {k} \ cdot \ mathbf {k} / 2}.}$

Cada onda separada gira apenas em fase no tempo, de modo que a solução transformada de Fourier dependente do tempo é

A transformada inversa de Fourier ainda é Gaussiana, mas agora o parâmetro a se tornou complexo e há um fator de normalização geral.

A integral de Ψ sobre todo o espaço é invariante, porque é o produto interno de Ψ com o estado de energia zero, que é uma onda com comprimento de onda infinito, uma função constante do espaço. Para qualquer autoestado de energia η ( x ) , o produto interno,

${\ displaystyle \ langle \ eta | \ psi \ rangle = \ int \ eta (\ mathbf {r}) \ psi (\ mathbf {r}) d ^ {3} \ mathbf {r},}$

apenas muda no tempo de forma simples: sua fase gira com uma frequência determinada pela energia de η . Quando η tem energia zero, como a onda de comprimento de onda infinito, ele não muda em nada.

O integral ∫ | Ψ | ² d ³ r também é invariante, o que é uma afirmação da conservação da probabilidade. Explicitamente,

em que √ a é a largura de P (r) em t = 0 ; r é a distância da origem; a velocidade da partícula é zero; e a origem de tempo t = 0 pode ser escolhida arbitrariamente.

A largura do Gaussiano é a quantidade interessante que pode ser lida a partir da densidade de probabilidade, | Ψ | ² ,

${\ displaystyle {\ sqrt {a ^ {2} + (\ hbar t / m) ^ {2} \ over a}}.}$

Essa largura eventualmente cresce linearmente no tempo, como ħt / (m√a) , indicando a propagação do pacote de ondas .

Por exemplo, se um pacote de onda de elétrons está inicialmente localizado em uma região de dimensões atômicas (ou seja, 10 ^-10 m), a largura do pacote dobra em cerca de 10 ^-16 s. Claramente, os pacotes de ondas de partículas se espalham muito rapidamente (no espaço livre): por exemplo, após 1 ms, a largura terá crescido para cerca de um quilômetro.

Este crescimento linear é um reflexo da incerteza do momento (invariante no tempo): o pacote de onda está confinado a um estreito Δ x = √ a / 2 e, portanto, tem um momento que é incerto (de acordo com o princípio da incerteza ) pela quantidade ħ / √ 2 a , um spread em velocidade de ħ / m √ 2 a , e portanto na posição futura de ħt / m √ 2 a . A relação de incerteza é então uma desigualdade estrita, muito longe da saturação, na verdade! A incerteza inicial Δ x Δ p = ħ / 2 agora aumentou por um fator de ħt / ma (para t grande ).

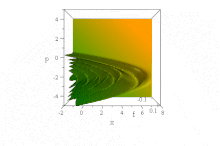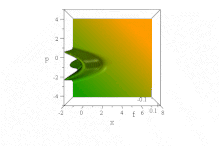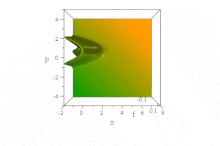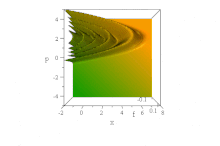
O trem de ondas Airy

Em contraste com o pacote de ondas gaussianas acima, foi observado que uma função de onda particular baseada em funções de Airy , se propaga livremente sem dispersão do envelope, mantendo sua forma. Ele acelera sem distorção na ausência de um campo de força: ψ = Ai ( B ( x - B ³ t ²)) exp (i B ³ t ( x −2 B ³ t ² / 3)) . (Para simplificar, ħ = 1, m = 1/2 e B é uma constante, cf. não dimensionalização .)

Visão truncada do desenvolvimento do tempo para a frente aérea no espaço de fase. (Clique para animar.)

No entanto, não há nenhuma dissonância com o teorema de Ehrenfest nesta situação sem força, porque o Estado é tanto não-normalizable e tem um indefinido (infinito) ⟨ x ⟩ para todos os tempos. (Na medida em que pode ser definido, ⟨ p ⟩ = 0 para todos os tempos, apesar do aparente aceleração da frente).

No espaço de fase , isso é evidente na distribuição de quase-probabilidade de Wigner de estado puro deste trem de ondas, cuja forma em x e p é invariante com o passar do tempo, mas cujas características aceleram para a direita, nas parábolas B aceleradas ( x - B ³ t ²) + ( p / B - tB ²) ² = 0 ,

${\ displaystyle {\ begin {alinhados} W (x, p; t) & = W (xB ^ {3} t ^ {2}, pB ^ {3} t; 0) \\ & = {1 \ over 2 ^ {1/3} \ pi B} ~ \ mathrm {Ai} \ left (2 ^ {2/3} \ left (Bx + {p ^ {2} \ over B ^ {2}} - 2Bpt \ right) \ direita). \ end {alinhado}}}$

Observe que a distribuição do momento obtida pela integração de todo x é constante. Uma vez que esta é a densidade de probabilidade no espaço de momento , é evidente que a função de onda em si não é normalizável.

Em 2018, a primeira observação experimental da fase cúbica de aceleração de pacotes de ondas Airy foi realizada por uma colaboração de pesquisadores de universidades israelenses, alemãs e americanas.

Propagador grátis

O limite estreita de largura do pacote de ondas solução Gaussiana discutido é o livre do kernel propagador K . Para outras equações diferenciais, este é geralmente chamado de função de Green, mas na mecânica quântica é tradicional para reservar função o nome de Green para a época transformada de Fourier de K .

Voltando a uma dimensão para simplificar, com m e ħ definidos iguais a um, quando a é a quantidade infinitesimal ε , a condição inicial gaussiana, reescalonada de modo que sua integral seja um,

${\ displaystyle \ psi _ {0} (x) = {1 \ over {\ sqrt {2 \ pi \ epsilon}}} e ^ {- {x ^ {2} \ over 2 \ epsilon}} \,}$

torna-se uma função delta , δ (x) , de modo que sua evolução no tempo,

${\ displaystyle K_ {t} (x) = {1 \ over {\ sqrt {2 \ pi (it + \ epsilon)}}} e ^ {- x ^ {2} \ over 2it + \ epsilon} \,}$

produz o propagador.

Observe que um pacote de onda inicial muito estreito torna-se instantaneamente infinitamente largo, mas com uma fase que é mais rapidamente oscilatória em grandes valores de x . Isso pode parecer estranho - a solução vai de ser localizado em um ponto para estar "em todos os lugares" em todos os momentos posteriores , mas é um reflexo da enorme incerteza do momentum de uma partícula localizada, conforme explicado acima.

Além disso, observe que a norma da função de onda é infinita, o que também é correto, uma vez que o quadrado de uma função delta é divergente da mesma maneira.

O fator envolvendo ε é uma quantidade infinitesimal que existe para garantir que as integrais sobre K sejam bem definidas. No limite que ε → 0, K torna-se puramente oscilatório e as integrais de K não são absolutamente convergentes. No restante desta seção, ele será definido como zero, mas para que todas as integrações sobre estados intermediários sejam bem definidas, o limite ε → 0 deve ser considerado apenas após o estado final ser calculado.

O propagador é a amplitude para atingir o ponto x no tempo t , ao partir da origem, x = 0. Por invariância de translação, a amplitude para atingir um ponto x ao começar no ponto y é a mesma função, só que agora traduzida,

${\ displaystyle K_ {t} (x, y) = K_ {t} (xy) = {1 \ over {\ sqrt {2 \ pi it}}} e ^ {i (xy) ^ {2} \ over 2t } \ ,.}$

No limite quando t é pequeno, o propagador, é claro, vai para uma função delta,

${\ displaystyle \ lim _ {t \ rightarrow 0} K_ {t} (xy) = \ delta (xy) ~,}$

mas apenas no sentido de distribuições : a integral dessa quantidade multiplicada por uma função de teste diferenciável arbitrária fornece o valor da função de teste em zero.

Para ver isso, observe que a integral sobre todo o espaço de K é igual a 1 em todos os momentos,

${\ displaystyle \ int K_ {t} (x) dx = 1 \ ,,}$

visto que essa integral é o produto interno de K com a função de onda uniforme. Mas o fator de fase no expoente tem uma derivada espacial diferente de zero em todos os lugares, exceto na origem e, portanto, quando o tempo é pequeno, ocorrem cancelamentos de fase rápidos em todos, exceto um ponto. Isso é rigorosamente verdadeiro quando o limite ε → 0 é obtido no final.

Portanto, o kernel de propagação é a evolução no tempo (futuro) de uma função delta, e é contínuo, em certo sentido: vai para a função delta inicial em pequenos momentos. Se a função de onda inicial é um pico infinitamente estreito na posição y ,

${\ displaystyle \ psi _ {0} (x) = \ delta (xy) \ ,,}$

torna-se a onda oscilatória,

${\ displaystyle \ psi _ {t} (x) = {1 \ over {\ sqrt {2 \ pi it}}} e ^ {i (xy) ^ {2} / 2t} \ ,.}$

Agora, uma vez que cada função pode ser escrita como uma soma ponderada de tais picos estreitos,

${\ displaystyle \ psi _ {0} (x) = \ int \ psi _ {0} (y) \ delta (xy) dy \ ,,}$

a evolução temporal de cada função ψ ₀ é determinada por este kernel de propagação K ,

Assim, esta é uma forma formal de expressar a solução fundamental ou solução geral . A interpretação dessa expressão é que a amplitude de uma partícula encontrada no ponto x no tempo t é a amplitude que ela começou em y , vezes a amplitude que ela passou de y para x , somada a todos os pontos de partida possíveis . Em outras palavras, é uma convolução do kernel K com a condição inicial arbitrária ψ ₀ ,

${\ displaystyle \ psi _ {t} = K * \ psi _ {0} \ ,.}$

Uma vez que a amplitude para viajar de x para y após um tempo t + t 'pode ser considerada em duas etapas, o propagador obedece à identidade da composição,

${\ displaystyle \ int K (xy; t) K (yz; t ') dy = K (xz; t + t') ~,}$

que pode ser interpretado da seguinte forma: a amplitude para viajar de x para z no tempo t + t 'é a soma da amplitude para viajar de x para y no tempo t , multiplicada pela amplitude para viajar de y para z no tempo t ', somado a todos os estados intermediários possíveis y . Esta é uma propriedade de um sistema quântico arbitrário e, ao subdividir o tempo em muitos segmentos, permite que a evolução do tempo seja expressa como uma integral de caminho .

Continuação analítica para difusão

O espalhamento de pacotes de ondas na mecânica quântica está diretamente relacionado ao espalhamento de densidades de probabilidade na difusão . Para uma partícula que está andando aleatoriamente , a função de densidade de probabilidade em qualquer ponto satisfaz a equação de difusão (veja também a equação de calor ),

${\ displaystyle {\ partial \ over \ partial t} \ rho = {1 \ over 2} {\ partial ^ {2} \ over \ partial x ^ {2}} \ rho ~,}$

onde o fator de 2, que pode ser removido pelo reescalonamento do tempo ou do espaço, é apenas por conveniência.

Uma solução para esta equação é a propagação Gaussiana,

${\ displaystyle \ rho _ {t} (x) = {1 \ over {\ sqrt {2 \ pi t}}} e ^ {- x ^ {2} \ over 2t} ~,}$

e, uma vez que a integral de ρ _t é constante, enquanto a largura está se tornando estreita em pequenos momentos, esta função se aproxima de uma função delta em t = 0,

${\ displaystyle \ lim _ {t \ rightarrow 0} \ rho _ {t} (x) = \ delta (x) \,}$

novamente apenas no sentido de distribuições, de modo que

${\ displaystyle \ lim _ {t \ rightarrow 0} \ int _ {x} f (x) \ rho _ {t} (x) = f (0) \,}$

para qualquer função de teste suave f .

A propagação Gaussiana é o núcleo de propagação da equação de difusão e obedece à identidade de convolução ,

${\ displaystyle K_ {t + t '} = K_ {t} * K_ {t'} \ ,,}$

que permite que a difusão seja expressa como uma integral de caminho. O propagador é o exponencial de um operador H ,

${\ displaystyle K_ {t} (x) = e ^ {- tH} \ ,,}$

que é o operador de difusão infinitesimal,

${\ displaystyle H = - {\ nabla ^ {2} \ over 2} \ ,.}$

Uma matriz possui dois índices, que no espaço contínuo a tornam uma função de x e x '. Neste caso, por causa da invariância de translação, o elemento da matriz K depende apenas da diferença da posição, e um abuso conveniente da notação é referir-se ao operador, aos elementos da matriz e à função da diferença com o mesmo nome:

${\ displaystyle K_ {t} (x, x ') = K_ {t} (x-x') \,}$

A invariância de translação significa que a multiplicação contínua da matriz,

${\ displaystyle C (x, x '') = \ int _ {x '} A (x, x') B (x ', x' ') \ ,,}$

é essencialmente convolução,

${\ displaystyle C (\ Delta) = C (x-x '') = \ int _ {x '} A (x-x') B (x'-x '') = \ int _ {y} A ( \ Delta -y) B (y) \ ,.}$

O exponencial pode ser definido ao longo de um intervalo de t s que incluem valores complexos, desde que integrais sobre o kernel de propagação permaneçam convergentes,

${\ displaystyle K_ {z} (x) = e ^ {- zH} \,}$

Contanto que a parte real de z seja positiva, para grandes valores de x , K é exponencialmente decrescente e as integrais sobre K são de fato absolutamente convergentes.

O limite desta expressão para z se aproximando do eixo imaginário puro é o propagador Schrödinger encontrado acima,

${\ displaystyle K_ {t} ^ {\ rm {Schr}} = K_ {it + \ epsilon} = e ^ {- (it + \ epsilon) H} \ ,,}$

que ilustra a evolução temporal das gaussianas acima.

Da identidade fundamental de exponenciação, ou integração de caminho,

${\ displaystyle K_ {z} * K_ {z '} = K_ {z + z'} \,}$

vale para todos os valores z complexos , onde as integrais são absolutamente convergentes, de modo que os operadores são bem definidos.

Assim, a evolução quântica de um Gaussiano, que é o núcleo de difusão complexo K ,

${\ displaystyle \ psi _ {0} (x) = K_ {a} (x) = K_ {a} * \ delta (x) \,}$

equivale ao estado evoluído no tempo,

${\ displaystyle \ psi _ {t} = K_ {it} * K_ {a} = K_ {a + it} \,}$

Isso ilustra a forma difusiva acima das soluções gaussianas complexas,

${\ displaystyle \ psi _ {t} (x) = {1 \ over {\ sqrt {2 \ pi (a + it)}}} e ^ {- {x ^ {2} \ over 2 (a + it) }} \ ,.}$

Veja também

Observações

Notas

Referências

• Einstein, Albert (1905), "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (On a Heuristic Viewpoint Concerning the Production and Transformation of Light)" (PDF) , Annalen der Physik , 17 (6): 132-148, bibcode : 1905AnP ... 322..132E , doi : 10.1002 / andp.19053220607Este artigo annus mirabilis sobre o efeito fotoelétrico foi recebido por Annalen der Physik em 18 de março de 1905.
• Schiff, Leonard I. (1968), mecânica quântica (terceira edição), Londres: McGraw-Hill
• Joy Manners (2000), Quantum Physics: An Introduction , CRC Press, pp. 53-56, ISBN 978-0-7503-0720-8
• Pauli, Wolfgang (2000), Wave Mechanics: Volume 5 de Pauli Lectures on Physics , Books on Physics, Dover Publications , ISBN 978-0486414621
• Abers, E .; Pearson, Ed (2004), Quantum Mechanics , Addison Wesley , Prentice-Hall Inc. , ISBN 978-0-13-146100-0
• Richard Fitzpatrick, Oscillations and Waves
• Berry, MV; Balazs, NL (1979), "Nonspreading wave packets", Am J Phys , 47 (47): 264-267, Bibcode : 1979AmJPh..47..264B , doi : 10.1119 / 1.11855
• Jackson, JD (1975), Classical Electrodynamics (2ª ed.), Nova York: John Wiley & Sons, Inc. , ISBN 978-0-471-43132-9
• Feynman, RP ; Hibbs, AR (1965), Quantum Mechanics and Path Integrals , Nova York: McGraw-Hill , ISBN 978-0-07-020650-2( Dover , 2010, ISBN  0-486-47722-3 .)
• Wheeler, Nicholas (2004), Energetics of a Gaussian wavepacket

links externos

• Materiais de aprendizagem relacionados ao movimento do pacote de ondas na Wikiversidade
• A definição do dicionário de pacote de ondas no Wikcionário
• Gráfico de pacote 1d Wave no Google
• 1d trem de ondas e gráfico de densidade de probabilidade no Google
• Gráfico de pacote 2d Wave no Google
• Gráfico do trem 2d Wave no Google
• Gráfico de densidade de probabilidade 2d no Google
• Uma simulação de um pacote de ondas em 2D (de acordo com FOURIER-Synthesis em 2D)
• Curtright, TL, funções de Wigner dependentes do tempo
• Web-Schödinger : Simulação interativa de dinâmica de pacotes de ondas 2D