Espaço Tychonoff - Tychonoff space
|
Axiomas de separação em espaços topológicos | |
|---|---|
| Classificação de Kolmogorov | |
| T 0 | (Kolmogorov) |
| T 1 | (Fréchet) |
| T 2 | (Hausdorff) |
| T 2 ½ | (Urysohn) |
| completamente T 2 | (completamente Hausdorff) |
| T 3 | (Hausdorff regular) |
| T 3½ | (Tychonoff) |
| T 4 | (Hausdorff normal) |
| T 5 | ( Hausdorff completamente normal ) |
| T 6 | ( Hausdorff perfeitamente normal ) |
Na topologia e nos ramos relacionados da matemática , os espaços de Tychonoff e os espaços completamente regulares são tipos de espaços topológicos . Essas condições são exemplos de axiomas de separação .
Os espaços Tychonoff têm o nome de Andrey Nikolayevich Tychonoff , cujo nome russo (Тихонов) é traduzido de várias maneiras como "Tychonov", "Tikhonov", "Tihonov", "Tichonov" etc., que os introduziu em 1930 para evitar a situação patológica de Hausdorff espaços cujas únicas funções contínuas de valor real são mapas constantes.
Definições
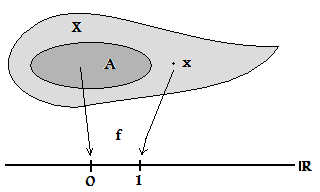
Um espaço topológico é chamado de completamente regular se os pontos podem ser separados de conjuntos fechados por meio de funções contínuas de valor real (limitadas). Em termos técnicos, isso significa: para qualquer conjunto fechado e qualquer ponto , existe uma função contínua com valor real tal que e (de forma equivalente, pode-se escolher quaisquer dois valores em vez de e e até mesmo exigir que seja uma função limitada.)
Um espaço topológico é chamado um espaço completamente regular (alternativamente: T 3½ espaço , ou t π espaço , ou completamente T 3 espaço ) se é um completamente regular espaço Hausdorff .
Observação. Espaços completamente regulares e espaços de Tychonoff são relacionados através da noção de equivalência de Kolmogorov . Um espaço topológico é Tychonoff se e somente se for completamente regular e T 0 . Por outro lado, um espaço é completamente regular se e somente se seu quociente de Kolmogorov for Tychonoff.
Convenções de nomenclatura
Em toda a literatura matemática, diferentes convenções são aplicadas quando se trata do termo "completamente regular" e dos axiomas "T". As definições nesta seção são de uso moderno típico. Alguns autores, no entanto, trocam os significados dos dois tipos de termos ou usam todos os termos de maneira intercambiável. Na Wikipedia, os termos "completamente regular" e "Tychonoff" são usados livremente e a anotação "T" geralmente é evitada. Na literatura padrão, recomenda-se cautela para descobrir quais definições o autor está usando. Para saber mais sobre esse assunto, consulte História dos axiomas de separação .
Exemplos e contra-exemplos
Quase todo espaço topológico estudado na análise matemática é Tychonoff, ou pelo menos completamente regular. Por exemplo, a linha real é Tychonoff sob a topologia euclidiana padrão . Outros exemplos incluem:
- Cada espaço métrico é Tychonoff; todo espaço pseudométrico é completamente regular.
- Todo espaço regular localmente compacto é completamente regular e, portanto, todo espaço localmente compacto de Hausdorff é Tychonoff.
- Em particular, toda variedade topológica é Tychonoff.
- Todo conjunto totalmente ordenado com a topologia de ordem é Tychonoff.
- Todo grupo topológico é completamente regular.
- Generalizando tanto os espaços métricos quanto os grupos topológicos, todo espaço uniforme é completamente regular. O inverso também é verdadeiro: todo espaço completamente regular é uniformizável.
- Cada complexo CW é Tychonoff.
- Todo espaço normal regular é completamente regular, e todo espaço normal de Hausdorff é Tychonoff.
- O avião Niemytzki é um exemplo de espaço Tychonoff que não é normal .
Propriedades
Preservação
A regularidade completa e a propriedade Tychonoff são bem comportadas em relação às topologias iniciais . Especificamente, a regularidade completa é preservada usando topologias iniciais arbitrárias e a propriedade Tychonoff é preservada usando topologias iniciais de separação de pontos. Segue que:
- Cada subespaço de um espaço completamente regular ou Tychonoff tem a mesma propriedade.
- Um espaço de produto não vazio é completamente regular (respectivamente Tychonoff) se e somente se cada espaço de fator for completamente regular (respectivamente Tychonoff).
Como todos os axiomas de separação, a regularidade completa não é preservada tomando topologias finais . Em particular, quocientes de espaços completamente regulares não precisam ser regulares . Os quocientes dos espaços de Tychonoff não precisam nem ser de Hausdorff . Existem quocientes fechados do plano de Moore que fornecem contra-exemplos.
Funções contínuas com valor real
Para qualquer espaço topológico X , seja C ( X ) a família de funções contínuas de valor real em X e seja C b ( X ) o subconjunto de funções contínuas de valor real limitadas .
Espaços completamente regulares podem ser caracterizados pelo fato de que sua topologia é completamente determinada por C ( X ) ou C b ( X ). Em particular:
- Um espaço X é completamente regular se e somente se tiver a topologia inicial induzida por C ( X ) ou C b ( X ).
- Um espaço X é completamente regular se e somente se cada conjunto fechado pode ser escrito como a interseção de uma família de conjuntos de zero em X (ou seja, os conjuntos de zero formam uma base para os conjuntos fechados de X ).
- Um espaço X é completamente regular se e somente se os conjuntos cozero de X formam uma base para a topologia de X .
Dado um espaço topológico arbitrário ( X , τ), existe uma maneira universal de associar um espaço completamente regular com ( X , τ). Seja ρ a topologia inicial em X induzida por C τ ( X ) ou, equivalentemente, a topologia gerada a partir dos conjuntos de cozero em ( X , τ). Então ρ será a melhor topologia completamente regular em X que é mais grosseira do que τ. Esta construção é universal no sentido de que qualquer função contínua
para um espaço completamente regular Y será contínuo em ( X , ρ). Na linguagem da teoria das categorias , o functor que envia ( X , τ) para ( X , ρ) é deixado adjunto ao functor de inclusão CReg → Top . Assim, a categoria de espaços completamente regulares CReg é uma subcategoria reflexiva de Top , a categoria de espaços topológicos . Ao tomar os quocientes de Kolmogorov , vê-se que a subcategoria dos espaços de Tychonoff também é reflexiva.
Pode-se mostrar que C τ ( X ) = C ρ ( X ) na construção acima, de modo que os anéis C ( X ) e C b ( X ) são tipicamente estudados apenas para espaços X completamente regulares .
A categoria de espaços de Tychonoff compactos reais é anti-equivalente à categoria dos anéis C ( X ) (onde X é compactado real) junto com homomorfismos de anéis como mapas. Por exemplo, pode-se reconstruir X a partir de C ( X ) quando X é (real) compacto. A teoria algébrica desses anéis é, portanto, objeto de estudos intensivos. Uma vasta generalização desta classe de anéis que ainda se assemelha a muitas propriedades dos espaços de Tychonoff, mas também é aplicável na geometria algébrica real , é a classe dos anéis fechados reais .
Embeddings
Os espaços Tychonoff são precisamente aqueles espaços que podem ser incorporados em espaços compactos de Hausdorff . Mais precisamente, para cada Tychonoff espaço X , existe um espaço compacto de Hausdorff K tal que X é homeomorfo a um subespaço de K .
Na verdade, sempre se pode escolher K como um cubo de Tychonoff (ou seja, um produto possivelmente infinito de intervalos de unidades ). Cada cubo de Tychonoff é compacto de Hausdorff como conseqüência do teorema de Tychonoff . Uma vez que cada subespaço de um espaço compacto de Hausdorff é Tychonoff, temos:
- Um espaço topológico é Tychonoff se, e somente se, puder ser embutido em um cubo Tychonoff .
Compactificações
De particular interesse são aqueles embeddings onde a imagem de X é densa em K ; estes são chamados de Hausdorff compactifications de X . Dado qualquer incorporação de um espaço completamente regular X num compacto Hausdorff espaço K o encerramento da imagem de X em K é um compactificaç~ao de X . No mesmo artigo de 1930 em que Tychonoff definiu espaços completamente regulares, ele também provou que cada espaço de Tychonoff tem uma compactação de Hausdorff.
Entre essas compactifications Hausdorff, existe um único "mais geral" um, o Pedra-Čech compactification β X . Caracteriza-se pela propriedade universal que, dada uma aplicação contínua f de X para qualquer outro espaço de Hausdorff compacto Y , existe um único mapa contínua g de β X para Y que se estende f no sentido em que f é a composição de g e j .
Estruturas uniformes
A regularidade completa é exatamente a condição necessária para a existência de estruturas uniformes em um espaço topológico. Em outras palavras, todo espaço uniforme tem uma topologia completamente regular e todo espaço X completamente regular é uniformizável . Um espaço topológico admite uma estrutura uniforme separada se e somente se for Tychonoff.
Dado um espaço completamente regular X geralmente há mais de uma uniformidade em X que é compatível com a topologia de X . No entanto, sempre haverá uma melhor uniformidade compatível, o chamado bem uniformidade em X . Se X é Tychonoff, em seguida, a estrutura uniforme pode ser escolhido de modo que β X torna-se a conclusão do espaço uniforme X .
Citações
Bibliografia
- Gillman, Leonard ; Jerison, Meyer (1960). Anéis de funções contínuas . Textos de Pós-Graduação em Matemática, nº 43 (edição reimpressa de Dover). NY: Springer-Verlag. p. xiii. ISBN 978-048681688-3.
- Narici, Lawrence ; Beckenstein, Edward (2011). Espaços vetoriais topológicos . Matemática pura e aplicada (segunda edição). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834 .
- Willard, Stephen (1970). Topologia geral (edição reimpressa de Dover). Reading, Massachusetts: Addison-Wesley Publishing Company. ISBN 0-486-43479-6.