Tetration - Tetration

Em matemática , tetration (ou hyper-4 ) é uma operação baseada em exponenciação iterada ou repetida . É a próxima hiperoperação após a exponenciação , mas antes da pentação . A palavra foi cunhada por Reuben Louis Goodstein a partir de tetra- (quatro) e iteração .

Sob a definição de exponenciação repetida, a notação de Rudy Rucker significa , onde n cópias de a são iteradas via exponenciação, da direita para a esquerda, ou seja, a aplicação de tempos de exponenciação . n é chamado de "altura" da função, enquanto a é chamado de "base", análogo à exponenciação. Ele seria lido como "o n º tetração de um ". ${\ displaystyle {^ {n} a}}$${\ displaystyle {a ^ {a ^ {\ cdot ^ {\ cdot ^ {a}}}}}}$${\ displaystyle n-1}$

Tetration também é definida recursivamente como

${\ displaystyle {^ {n} a}: = {\ begin {cases} 1 & {\ text {if}} n = 0 \\ a ^ {\ left (^ {(n-1)} a \ right)} & {\ text {if}} n> 0 \ end {casos}}}$,

permitindo tentativas de estender a tetração a números não naturais, como números reais e complexos.

Os dois inversos de tetração são chamados de super-raiz eo superlogaritmo , análoga à raiz enésima e as funções logarítmicas. Nenhuma das três funções é elementar .

A tetração é usada para a notação de números muito grandes .

Introdução

As primeiras quatro hiperoperações são mostradas aqui, com a tetração sendo considerada a quarta da série. A sucessão de operação unária , definida como , é considerada a operação zero. ${\ displaystyle a '= a + 1}$

1. Adição

   ${\ displaystyle a + n = a + \ underbrace {1 + 1 + \ cdots +1} _ {n}}$

   n cópias de 1 adicionadas a a .

2. Multiplicação

   ${\ displaystyle a \ times n = \ underbrace {a + a + \ cdots + a} _ {n}}$

   n cópias de um combinado por adição.

3. Exponenciação

   ${\ displaystyle a ^ {n} = \ underbrace {a \ times a \ times \ cdots \ times a} _ {n}}$

   n cópias de um combinado por multiplicação.

4. Tetration

   ${\ displaystyle {^ {n} a} = \ underbrace {a ^ {a ^ {\ cdot ^ {\ cdot ^ {a}}}}} _ {n}}$

   n cópias de a combinadas por exponenciação, da direita para a esquerda.

A sucessão, ( a ′ = a + 1) , é a operação mais básica; enquanto adição ( a + n ) é uma operação primária, para adição de números naturais ela pode ser considerada como uma sucessão encadeada de n sucessores de a ; a multiplicação ( a  ×  n ) também é uma operação primária, embora para números naturais possa ser analogamente considerada como uma adição encadeada envolvendo n números de a . A exponenciação pode ser considerada como uma multiplicação encadeada envolvendo n números de a e tetration ( ) como uma potência encadeada envolvendo n números a . Cada uma das operações acima são definidas pela iteração da anterior; entretanto, ao contrário das operações anteriores, a tetração não é uma função elementar . ${\ displaystyle ^ {n} a \!}$

O parâmetro a é referido como a base , enquanto o parâmetro n pode ser referido como a altura . Na definição original de tetração, o parâmetro de altura deve ser um número natural; por exemplo, seria ilógico dizer "três elevou-se a si mesmo negativo cinco vezes" ou "quatro elevou-se a si mesmo metade de uma vez". No entanto, assim como adição, multiplicação e exponenciação podem ser definidas de maneiras que permitem extensões para números reais e complexos, várias tentativas foram feitas para generalizar a tetração para números negativos, números reais e números complexos. Uma forma de fazer isso é usar uma definição recursiva para tetração; para qualquer número inteiro positivo real e não negativo , podemos definir recursivamente como: ${\ displaystyle a> 0}$ ${\ displaystyle n \ geq 0}$${\ displaystyle \, \! {^ {n} a}}$

${\ displaystyle {^ {n} a}: = {\ begin {cases} 1 & {\ text {if}} n = 0 \\ a ^ {\ left (^ {(n-1)} a \ right)} & {\ text {if}} n> 0 \ end {casos}}}$

A definição recursiva é equivalente à exponenciação repetida para alturas naturais ; no entanto, esta definição permite extensões para as outras alturas, tais como , e bem - muitas dessas extensões são áreas de pesquisa ativa. ${\ displaystyle ^ {0} a}$${\ displaystyle ^ {- 1} a}$${\ displaystyle ^ {i} a}$

Terminologia

Existem muitos termos para tetração, cada um dos quais tem alguma lógica por trás dele, mas alguns não se tornaram comumente usados ​​por uma razão ou outra. Aqui está uma comparação de cada termo com seu fundamento lógico e contra-raciocínio.

• O termo tetration , introduzido por Goodstein em seu artigo de 1947 Transfinite Ordinals in Recursive Number Theory (generalizando a representação de base recursiva usada no teorema de Goodstein para usar operações superiores), ganhou domínio. Ele também foi popularizado em Rudy Rucker do Infinito e da Mente .
• O termo superexponenciação foi publicado por Bromer em seu artigo Superexponenciação em 1987. Foi usado anteriormente por Ed Nelson em seu livro Predicative Arithmetic, Princeton University Press, 1986.
• O termo hiperpotência é uma combinação natural de hiper e potência , que descreve apropriadamente a tetração. O problema está no significado de hiper em relação à sequência de hiperoperação . Ao considerar as hiperoperações, o termo hiper se refere a todas as categorias, e o termo super se refere à categoria 4, ou tetração. Portanto, sob essas considerações, o hiperpoder é enganoso, uma vez que se refere apenas à tetração.
• O termo torre de energia é usado ocasionalmente, na forma "a torre de energia de ordem n " para . Este é um nome impróprio, entretanto, porque a tetração não pode ser expressa com funções de potência iteradas (veja acima), uma vez que é uma função exponencial iterada .${\ displaystyle {\ \ atop {\}} {{\ underbrace {a ^ {a ^ {\ cdot ^ {\ cdot ^ {a}}}}}} \ atop n}}$

Devido em parte a alguma terminologia compartilhada e simbolismo notacional semelhante , a tetração é freqüentemente confundida com funções e expressões intimamente relacionadas. Aqui estão alguns termos relacionados:

Termos relacionados à tetração

Terminologia	Forma
Tetration	${\ displaystyle a ^ {a ^ {\ cdot ^ {\ cdot ^ {a ^ {a}}}}}}$
Exponenciais iteradas	${\ displaystyle a ^ {a ^ {\ cdot ^ {\ cdot ^ {a ^ {x}}}}}}$
Exponenciais aninhadas (também torres)	${\ displaystyle a_ {1} ^ {a_ {2} ^ {\ cdot ^ {\ cdot ^ {a_ {n}}}}}}$
Exponenciais infinitas (também torres)	${\ displaystyle a_ {1} ^ {a_ {2} ^ {a_ {3} ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}}}}$

Nas primeiras duas expressões, a é a base e o número de vezes que a aparece é a altura (adicione um para x ). Na terceira expressão, n é a altura , mas cada uma das bases é diferente.

Cuidados devem ser tomados quando se refere a exponenciais iterativos, como é comum chamar expressões dessa forma iterada exponenciação, que é ambígua, pois isso pode significar iteradas poderes ou iterated exponenciais .

Notação

Existem muitos estilos de notação diferentes que podem ser usados ​​para expressar a tetração. Algumas notações também podem ser usadas para descrever outras hiperoperações , enquanto algumas são limitadas à tetração e não têm extensão imediata.

Estilos de notação para tetração

Nome	Forma	Descrição
Notação de Rudy Rucker	${\ displaystyle \, {} ^ {n} a}$	Usado por Maurer [1901] e Goodstein [1947]; O livro de Rudy Rucker , Infinity and the Mind, popularizou a notação.
Notação de seta para cima de Knuth	${\ displaystyle a {\ uparrow \ uparrow} n}$	Permite a extensão colocando mais setas ou, ainda mais poderosamente, uma seta indexada.
Notação de seta em cadeia de Conway	${\ displaystyle a \ rightarrow n \ rightarrow 2}$	Permite a extensão aumentando o número 2 (equivalente às extensões acima), mas também, de forma ainda mais poderosa, estendendo a cadeia
Função Ackermann	${\ displaystyle {} ^ {n} 2 = \ operatorname {A} (4, n-3) +3}$	Permite que o caso especial seja escrito em termos da função Ackermann. ${\ displaystyle a = 2}$
Notação exponencial iterada	${\ displaystyle \ exp _ {a} ^ {n} (1)}$	Permite extensão simples para exponenciais iteradas de valores iniciais diferentes de 1.
Notações Hooshmand	${\ displaystyle {\ begin {alinhado} & \ operatorname {uxp} _ {a} n \\ [2pt] & a ^ {\ frac {n} {}} \ end {alinhado}}}$	Usado por MH Hooshmand [2006].
hiperoperação notações	${\ displaystyle {\ begin {alinhado} & a [4] n \\ [2pt] & H_ {4} (a, n) \ end {alinhado}}}$	Permite extensão aumentando o número 4; isso dá a família de hiperoperações .
Notação de acento circunflexo duplo	a^^n	Visto que a seta para cima é usada de forma idêntica ao acento circunflexo ( ^), a tetração pode ser escrita como ( ^^); conveniente para ASCII .

Uma notação acima usa notação exponencial iterada; isso é definido em geral da seguinte forma:

${\ displaystyle \ exp _ {a} ^ {n} (x) = a ^ {a ^ {\ cdot ^ {\ cdot ^ {a ^ {x}}}}}}$com n a s.

Não há tantas notações para exponenciais iteradas, mas aqui estão algumas:

Estilos de notação para exponenciais iteradas

Nome	Forma	Descrição
Notação padrão	${\ displaystyle \ exp _ {a} ^ {n} (x)}$	Euler cunhou a notação , e a notação de iteração existe há quase tanto tempo. ${\ displaystyle \ exp _ {a} (x) = a ^ {x}}$${\ displaystyle f ^ {n} (x)}$
Notação de seta para cima de Knuth	${\ displaystyle (a {\ uparrow}) ^ {n} (x)}$	Permite superpotências e função superexponencial aumentando o número de flechas; usado no artigo em grandes números .
Notação de texto	exp_a^n(x)	Com base na notação padrão; conveniente para ASCII .
Notação J	x^^:(n-1)x	Repete a exponenciação. Veja J (linguagem de programação)

Exemplos

Devido ao crescimento extremamente rápido da tetração, a maioria dos valores na tabela a seguir são grandes demais para serem escritos em notação científica. Nesses casos, a notação exponencial iterada é usada para expressá-los na base 10. Os valores contendo um ponto decimal são aproximados.

Exemplos de tetração

${\ displaystyle x}$	${\ displaystyle {} ^ {2} x}$	${\ displaystyle {} ^ {3} x}$	${\ displaystyle {} ^ {4} x}$	${\ displaystyle {} ^ {5} x}$
1	1	1	1	1
2	4	16	65.536	2 65.536 ou (2,0035 × 10 19.728 )
3	27	7.625.597.484.987	${\ displaystyle \ exp _ {10} ^ {3} (1.09902)}$(3,6 × 10 12 dígitos)	${\ displaystyle \ exp _ {10} ^ {4} (1.09902)}$
4	256	1,34078 × 10 154	${\ displaystyle \ exp _ {10} ^ {3} (2.18726)}$(8,1 × 10 153 dígitos)	${\ displaystyle \ exp _ {10} ^ {4} (2.18726)}$
5	3.125	1,91101 × 10 2.184	${\ displaystyle \ exp _ {10} ^ {3} (3.33928)}$(1,3 × 10 2.184 dígitos)	${\ displaystyle \ exp _ {10} ^ {4} (3.33928)}$
6	46.656	2.65912 × 10 36.305	${\ displaystyle \ exp _ {10} ^ {3} (4,55997)}$(2,1 × 10 36.305 dígitos)	${\ displaystyle \ exp _ {10} ^ {4} (4,55997)}$
7	823.543	3,75982 × 10 695,974	${\ displaystyle \ exp _ {10} ^ {3} (5,84259)}$(3,2 × 10 695.974 dígitos)	${\ displaystyle \ exp _ {10} ^ {4} (5,84259)}$
8	16.777.216	6.01452 × 10 15.151.335	${\ displaystyle \ exp _ {10} ^ {3} (7.18045)}$(5,4 × 10 15.151.335 dígitos)	${\ displaystyle \ exp _ {10} ^ {4} (7.18045)}$
9	387.420.489	4,28125 × 10 369,693,099	${\ displaystyle \ exp _ {10} ^ {3} (8.56784)}$(4,1 × 10 369.693.099 dígitos)	${\ displaystyle \ exp _ {10} ^ {4} (8.56784)}$
10	10.000.000.000	10 10.000.000.000	${\ displaystyle \ exp _ {10} ^ {3} (10)}$(10 10.000.000.000 + 1 dígito)	${\ displaystyle \ exp _ {10} ^ {4} (10)}$

Propriedades

A tetração tem várias propriedades semelhantes à exponenciação, bem como propriedades que são específicas da operação e são perdidas ou ganhas com a exponenciação. Como a exponenciação não comuta , as regras de produto e potência não têm um análogo com tetração; as afirmações e não são verdadeiras para a maioria dos casos. ${\ textstyle {} ^ {a} \ left ({} ^ {b} x \ right) = \ left ({} ^ {ab} x \ right)}$${\ textstyle {} ^ {a} \ left (xy \ right) = {} ^ {a} x {} ^ {a} y}$

No entanto, a tetração segue uma propriedade diferente, na qual . Este fato é mais claramente mostrado usando a definição recursiva. A partir desta propriedade, a prova segue-se que , o que permite a comutação b e c em certas equações. A prova é a seguinte: ${\ textstyle {} ^ {a} x = x ^ {\ left ({} ^ {a-1} x \ right)}}$${\ displaystyle \ left ({} ^ {b} a \ right) ^ {\ left ({} ^ {c} a \ right)} = \ left ({} ^ {c + 1} a \ right) ^ { \ left ({} ^ {b-1} a \ right)}}$

${\ displaystyle {\ begin {alinhado} & \ left ({} ^ {b} a \ right) ^ {\ left ({} ^ {c} a \ right)} \\ = {} & \ left (a ^ {{} ^ {b-1} a} \ right) ^ {\ left ({} ^ {c} a \ right)} \\ = {} & a ^ {\ left ({} ^ {b-1} a \ right) \ left ({} ^ {c} a \ right)} \\ = {} & a ^ {\ left ({} ^ {c} a \ right) \ left ({} ^ {b-1} a \ right)} \\ = {} & \ left ({} ^ {c + 1} a \ right) ^ {\ left ({} ^ {b-1} a \ right)} \ end {alinhado}}}$

Quando um número x e 10 são coprimes , é possível calcular os últimos m dígitos decimais usando o teorema de Euler , para qualquer inteiro m . ${\ displaystyle \, \! \ ^ {a} x}$

Direção de avaliação

Ao avaliar a tetração expressa como uma "torre de exponenciação", a exponenciação serial é feita no nível mais profundo primeiro (na notação, no ápice). Por exemplo:

${\ displaystyle \, \! \ ^ {4} 2 = 2 ^ {2 ^ {2 ^ {2}}} = 2 ^ {\ left (2 ^ {\ left (2 ^ {2} \ right)} \ direita)} = 2 ^ {\ esquerda (2 ^ {4} \ direita)} = 2 ^ {16} = 65, \! 536}$

Essa ordem é importante porque a exponenciação não é associativa e avaliar a expressão na ordem oposta levará a uma resposta diferente:

${\ displaystyle \, \! 2 ^ {2 ^ {2 ^ {2}}} \ neq \ left ({\ left (2 ^ {2} \ right)} ^ {2} \ right) ^ {2} = 4 ^ {2 \ cdot 2} = 256}$

Avaliar a expressão da esquerda para a direita é considerado menos interessante; avaliando da esquerda para a direita, qualquer expressão pode ser simplificada para ser . Por isso, as torres devem ser avaliadas da direita para a esquerda (ou de cima para baixo). Os programadores de computador referem-se a essa escolha como associativa à direita . ${\ displaystyle ^ {n} a \!}$${\ displaystyle a ^ {\ left (a ^ {n-1} \ right)} \! \!}$

Extensões

A tetração pode ser estendida de duas maneiras diferentes; na equação , tanto a base a quanto a altura n podem ser generalizadas usando a definição e as propriedades de tetração. Embora a base e a altura possam ser estendidas além dos inteiros não negativos para diferentes domínios , incluindo funções complexas como e alturas de n infinito , as propriedades mais limitadas de tetração reduzem a capacidade de estender a tetração. ${\ displaystyle ^ {n} a \!}$${\ displaystyle {^ {n} 0}}$${\ displaystyle {} ^ {n} i}$

Extensão de domínio para bases

Base zero

O exponencial não é definido de forma consistente. Assim, as tetrações não são claramente definidas pela fórmula dada anteriormente. No entanto, está bem definido e existe: ${\ displaystyle 0 ^ {0}}$${\ displaystyle \, {^ {n} 0}}$${\ displaystyle \ lim _ {x \ rightarrow 0} {} ^ {n} x}$

${\ displaystyle \ lim _ {x \ rightarrow 0} {} ^ {n} x = {\ begin {cases} 1, & n {\ text {even}} \\ 0, & n {\ text {odd}} \ end {casos}}}$

Assim, poderíamos definir de forma consistente . Isso é análogo a definir . ${\ displaystyle {} ^ {n} 0 = \ lim _ {x \ rightarrow 0} {} ^ {n} x}$${\ displaystyle 0 ^ {0} = 1}$

Sob esta extensão,, então a regra da definição original ainda é válida. ${\ displaystyle {} ^ {0} 0 = 1}$${\ displaystyle {^ {0} a} = 1}$

Bases complexas

Uma vez que os números complexos pode ser aumentada para potências, tetração pode ser aplicado a bases da forma z = um + bi (onde um e b são reais). Por exemplo, em ⁿ z com z = i , a tetração é obtida usando o ramo principal do logaritmo natural; usando a fórmula de Euler , obtemos a relação:

${\ displaystyle i ^ {a + bi} = e ^ {{\ frac {1} {2}} {\ pi i} (a + bi)} = e ^ {- {\ frac {1} {2}} {\ pi b}} \ left (\ cos {\ frac {\ pi a} {2}} + i \ sin {\ frac {\ pi a} {2}} \ right)}$

Isso sugere uma definição recursiva para ^{n +1} i = a ′ + b′i dado qualquer ⁿ i = a + bi :

${\ displaystyle {\ begin {align} a '& = e ^ {- {\ frac {1} {2}} {\ pi b}} \ cos {\ frac {\ pi a} {2}} \\ [ 2pt] b '& = e ^ {- {\ frac {1} {2}} {\ pi b}} \ sin {\ frac {\ pi a} {2}} \ end {alinhado}}}$

Os seguintes valores aproximados podem ser derivados:

Valores de tetração de bases complexas

${\ textstyle {} ^ {n} i}$	Valor aproximado
${\ textstyle {} ^ {1} i = i}$	eu
${\ textstyle {} ^ {2} i = i ^ {\ left ({} ^ {1} i \ right)}}$	0,2079
${\ textstyle {} ^ {3} i = i ^ {\ left ({} ^ {2} i \ right)}}$	0,9472 + 0,3208 i
${\ textstyle {} ^ {4} i = i ^ {\ left ({} ^ {3} i \ right)}}$	0,0501 + 0,6021 i
${\ textstyle {} ^ {5} i = i ^ {\ left ({} ^ {4} i \ right)}}$	0,3872 + 0,0305 i
${\ textstyle {} ^ {6} i = i ^ {\ left ({} ^ {5} i \ right)}}$	0,7823 + 0,5446 i
${\ textstyle {} ^ {7} i = i ^ {\ left ({} ^ {6} i \ right)}}$	0,1426 + 0,4005 i
${\ textstyle {} ^ {8} i = i ^ {\ left ({} ^ {7} i \ right)}}$	0,5198 + 0,1184 i
${\ textstyle {} ^ {9} i = i ^ {\ left ({} ^ {8} i \ right)}}$	0,5686 + 0,6051 i

Resolvendo a relação inversa, como na seção anterior, resulta o esperado ⁰ i = 1 e ⁻¹ i = 0 , com valores negativos de n dando resultados infinitos no eixo imaginário. Traçada no plano complexo , toda a sequência gira até o limite 0,4383 + 0,3606 i , o que pode ser interpretado como o valor em que n é infinito.

Essas sequências de tetração têm sido estudadas desde a época de Euler, mas são mal compreendidas devido ao seu comportamento caótico. A maioria das pesquisas publicadas tem focado historicamente na convergência da função exponencial infinitamente iterada. A pesquisa atual tem se beneficiado muito com o advento de computadores poderosos com software fractal e matemática simbólica. Muito do que se sabe sobre a tetração vem do conhecimento geral da dinâmica complexa e da pesquisa específica do mapa exponencial.

Extensões do domínio para diferentes alturas

Alturas infinitas

A tetração pode ser estendida a alturas infinitas ; ou seja, para certos valores de a e n em , existe um resultado bem definido para um n infinito . Isso ocorre porque, para bases dentro de um determinado intervalo, a tetração converge para um valor finito à medida que a altura tende para o infinito . Por exemplo, converge para 2 e, portanto, pode ser considerado igual a 2. A tendência para 2 pode ser vista avaliando uma pequena torre finita: ${\ displaystyle {} ^ {n} a}$${\ displaystyle {\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}}}}$

${\ displaystyle {\ begin {align} {\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2 }} ^ {1,414}}}}} & \ approx {\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {1,63 }}}} \\ & \ approx {\ sqrt {2}} ^ {{\ sqrt {2}} ^ {{\ sqrt {2}} ^ {1,76}}} \\ & \ approx {\ sqrt {2 }} ^ {{\ sqrt {2}} ^ {1,84}} \\ & \ approx {\ sqrt {2}} ^ {1,89} \\ & \ approx 1,93 \ end {alinhado}}}$

Em geral, o exponencial infinitamente iterado , definido como o limite de conforme n vai ao infinito, converge para e ^{- e} ≤ x ≤ e ^{1 / e} , aproximadamente no intervalo de 0,066 a 1,44, resultado mostrado por Leonhard Euler . O limite, se existir, é uma solução real positiva da equação y = x ^y . Portanto, x = y ^{1 / y} . O limite que define a exponencial infinita de x não existe quando x > e ^{1 / e} porque o máximo de y ^{1 / y} é e ^{1 / e} . O limite também deixa de existir quando 0 < x < e ^{- e} . ${\ displaystyle x ^ {x ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}} \! \!}$${\ displaystyle {} ^ {n} x}$

Isso pode ser estendido para números complexos z com a definição:

${\ displaystyle {} ^ {\ infty} z = z ^ {z ^ {\ cdot ^ {\ cdot ^ {\ cdot}}}} = {\ frac {\ mathrm {W} (- \ ln {z}) } {- \ ln {z}}} ~,}$

onde W representa a função W de Lambert .

Como o limite y = ^∞ x (se existente na reta real positiva, ou seja, para e ^{- e} ≤ x ≤ e ^{1 / e} ) deve satisfazer x ^y = y , vemos que x ↦ y = ^∞ x is (o ramo inferior de ) a função inversa de y ↦ x = y ^{1 / y} .

Alturas negativas

Podemos usar a regra recursiva para tetração,

${\ displaystyle {^ {k + 1} a} = a ^ {\ left ({^ {k} a} \ right)},}$

para provar : ${\ displaystyle {} ^ {- 1} a}$

${\ displaystyle ^ {k} a = \ log _ {a} \ left (^ {k + 1} a \ right);}$

Substituindo −1 por k resulta

${\ displaystyle {} ^ {- 1} a = \ log _ {a} \ left ({} ^ {0} a \ right) = \ log _ {a} 1 = 0}$.

Valores negativos menores não podem ser bem definidos dessa maneira. Substituindo −2 por k na mesma equação dá

${\ displaystyle {} ^ {- 2} a = \ log _ {a} \ left ({} ^ {- 1} a \ right) = \ log _ {a} 0 = - \ infty}$

que não está bem definido. Eles podem, no entanto, às vezes ser considerados conjuntos.

Pois , qualquer definição de é consistente com a regra porque ${\ displaystyle n = 1}$${\ displaystyle \, \! {^ {- 1} 1}}$

${\ displaystyle {^ {0} 1} = 1 = 1 ^ {n}}$para qualquer .${\ displaystyle \, \! n = {^ {- 1} 1}}$

Alturas reais

No momento, não existe uma solução comumente aceita para o problema geral de estender a tetração aos valores reais ou complexos de n . No entanto, houve várias abordagens para o problema e diferentes abordagens são descritas abaixo.

Em geral, o problema é encontrar - para qualquer real a > 0 - uma função superexponencial sobre real x > −2 que satisfaça ${\ displaystyle \, f (x) = {} ^ {x} a}$

• ${\ displaystyle \, {} ^ {- 1} a = 0}$
• ${\ displaystyle \, {} ^ {0} a = 1}$
• ${\ displaystyle \, {} ^ {x} a = a ^ {\ left ({} ^ {x-1} a \ right)}}$para tudo real ${\ displaystyle x> -1.}$

Para encontrar uma extensão mais natural, geralmente são necessários um ou mais requisitos extras. Geralmente é uma coleção do seguinte:

• Um requisito de continuidade (geralmente apenas que é contínuo em ambas as variáveis ​​para ).${\ displaystyle {} ^ {x} a}$${\ displaystyle x> 0}$
• Um requisito de diferenciabilidade (pode ser uma, duas, k vezes ou infinitamente diferenciável em x ).
• Um requisito de regularidade (implicando duas vezes diferenciável em x ) que:

${\ displaystyle \ left ({\ frac {d ^ {2}} {dx ^ {2}}} f (x)> 0 \ right)}$ para todos ${\ displaystyle x> 0}$

O quarto requisito difere de autor para autor e entre as abordagens. Existem duas abordagens principais para estender a tetração a alturas reais; um é baseado no requisito de regularidade e o outro é baseado no requisito de diferenciabilidade . Essas duas abordagens parecem ser tão diferentes que podem não ser conciliadas, pois produzem resultados inconsistentes entre si.

Quando é definido para um intervalo de comprimento um, toda a função segue facilmente para todo x > −2 . ${\ displaystyle \, {} ^ {x} a}$

Aproximação linear para alturas reais

Uma aproximação linear (solução para o requisito de continuidade, aproximação para o requisito de diferenciabilidade) é dada por:

${\ displaystyle {} ^ {x} a \ approx {\ begin {cases} \ log _ {a} \ left (^ {x + 1} a \ right) & x \ leq -1 \\ 1 + x & -1 < x \ leq 0 \\ a ^ {\ left (^ {x-1} a \ right)} & 0 <x \ end {cases}}}$

portanto:

Valores de aproximação linear

Aproximação	Domínio
${\ textstyle {} ^ {x} a \ approx x + 1}$	para −1 < x <0
${\ textstyle {} ^ {x} a \ approx a ^ {x}}$	para 0 < x <1
${\ textstyle {} ^ {x} a \ approx a ^ {a ^ {(x-1)}}}$	para 1 < x <2

e assim por diante. No entanto, é apenas diferenciável por partes; em valores inteiros de x, a derivada é multiplicada por . É continuamente diferenciável para se e somente se . Por exemplo, usando esses métodos e${\ displaystyle \ ln {a}}$${\ displaystyle x> -2}$${\ displaystyle a = e}$${\ displaystyle {} ^ {\ frac {\ pi} {2}} e \ aproximadamente 5,868 ...}$${\ displaystyle {} ^ {- 4,3} 0,5 \ aproximadamente 4,03335 ...}$

Um teorema principal no artigo de Hooshmand afirma: Let . Se é contínuo e satisfaz as condições: ${\ displaystyle 0 <a \ neq 1}$${\ displaystyle f: (- 2, + \ infty) \ rightarrow \ mathbb {R}}$

• ${\ displaystyle f (x) = a ^ {f (x-1)} \; \; {\ text {para todos}} \; \; x> -1, \; f (0) = 1,}$
• ${\ displaystyle f}$é diferenciável em (-1, 0) ,
• ${\ displaystyle f ^ {\ prime}}$é uma função não decrescente ou não crescente em (-1, 0) ,
• ${\ displaystyle f ^ {\ prime} \ left (0 ^ {+} \ right) = (\ ln a) f ^ {\ prime} \ left (0 ^ {-} \ right) {\ text {ou}} f ^ {\ prime} \ left (-1 ^ {+} \ right) = f ^ {\ prime} \ left (0 ^ {-} \ right).}$

então é determinado exclusivamente através da equação ${\ displaystyle f}$

${\ displaystyle f (x) = \ exp _ {a} ^ {[x]} \ left (a ^ {(x)} \ right) = \ exp _ {a} ^ {[x + 1]} (( x)) \ quad {\ text {para todos}} \; \; x> -2,}$

onde denota a parte fracionária de x e é o - função iterado da função . ${\ displaystyle (x) = x- [x]}$${\ displaystyle \ exp _ {a} ^ {[x]}}$${\ displaystyle [x]}$${\ displaystyle \ exp _ {a}}$

A prova é que da segunda à quarta condições implicam trivialmente que f é uma função linear em [−1, 0] .

A aproximação linear da função de tetração natural é continuamente diferenciável, mas sua segunda derivada não existe em valores inteiros de seu argumento. Hooshmand derivou outro teorema de exclusividade para ele que afirma: ${\ displaystyle {} ^ {x} e}$

Se é uma função contínua que satisfaz: ${\ displaystyle f: (- 2, + \ infty) \ rightarrow \ mathbb {R}}$

• ${\ displaystyle f (x) = e ^ {f (x-1)} \; \; {\ text {para todos}} \; \; x> -1, \; f (0) = 1,}$
• ${\ displaystyle f}$é convexo em (-1, 0) ,
• ${\ displaystyle f ^ {\ prime} \ left (0 ^ {-} \ right) \ leq f ^ {\ prime} \ left (0 ^ {+} \ right).}$

então . [Aqui está o nome de Hooshmand para a aproximação linear da função de tetração natural.] ${\ displaystyle f = {\ text {uxp}}}$${\ displaystyle f = {\ text {uxp}}}$

A prova é praticamente a mesma de antes; a equação de recursão garante que e então a condição de convexidade implica que é linear em (-1, 0) . ${\ displaystyle f ^ {\ prime} (- 1 ^ {+}) = f ^ {\ prime} (0 ^ {+}),}$${\ displaystyle f}$

Portanto, a aproximação linear para tetração natural é a única solução da equação e que é convexa em (−1, + ∞) . Todas as outras soluções suficientemente diferenciáveis ​​devem ter um ponto de inflexão no intervalo (-1, 0) . ${\ displaystyle f (x) = e ^ {f (x-1)} \; \; (x> -1)}$${\ displaystyle f (0) = 1}$

Aproximações de ordem superior para alturas reais

Além das aproximações lineares, uma aproximação quadrática (para o requisito de diferenciabilidade) é dada por:

${\ displaystyle {} ^ {x} a \ approx {\ begin {cases} \ log _ {a} \ left ({} ^ {x + 1} a \ right) & x \ leq -1 \\ 1 + {\ frac {2 \ ln (a)} {1 \; + \; \ ln (a)}} x - {\ frac {1 \; - \; \ ln (a)} {1 \; + \; \ ln (a)}} x ^ {2} & - 1 <x \ leq 0 \\ a ^ {\ left ({} ^ {x-1} a \ right)} & x> 0 \ end {cases}}}$

que é diferenciável para todos , mas não duas vezes diferenciável. Por exemplo, If é o mesmo que a aproximação linear. ${\ displaystyle x> 0}$${\ displaystyle {} ^ {\ frac {1} {2}} 2 \ aproximadamente 1,45933 ...}$${\ displaystyle a = e}$

Devido à forma como é calculada, esta função não "cancela", ao contrário dos expoentes, onde . Nomeadamente, ${\ displaystyle \ left (a ^ {\ frac {1} {n}} \ right) ^ {n} = a}$

${\ displaystyle {} ^ {n} \ left ({} ^ {\ frac {1} {n}} a \ right) = \ underbrace {\ left ({} ^ {\ frac {1} {n}} a \ right) ^ {\ left ({} ^ {\ frac {1} {n}} a \ right) ^ {\ cdot ^ {\ cdot ^ {\ cdot ^ {\ cdot ^ {\ left ({} ^ { \ frac {1} {n}} a \ right)}}}}}}} _ {n} \ neq a}$.

Assim como existe uma aproximação quadrática, aproximações cúbicas e métodos para generalizar para aproximações de grau n também existem, embora sejam muito mais difíceis de manejar.

Alturas complexas

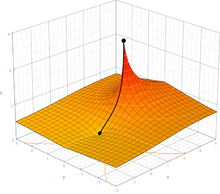
Agora foi provado que existe uma função única F que é uma solução da equação F ( z + 1) = exp ( F ( z )) e satisfaz as condições adicionais que F (0) = 1 e F ( z ) aproxima-se dos pontos fixos do logaritmo (aproximadamente 0,318 ± 1,337 i ) conforme z se aproxima de ± i ∞ e que F é holomórfico em todo o plano z complexo , exceto a parte do eixo real em z ≤ −2 . Esta prova confirma uma conjectura anterior . A construção de tal função foi demonstrada originalmente por Kneser em 1950. O mapa complexo desta função é mostrado na figura à direita. A prova também funciona para outras bases além de e , desde que a base seja maior que . O trabalho subsequente estendeu a construção a todas as bases complexas. A complexa aproximação de precisão dupla desta função está disponível online. ${\ displaystyle e ^ {\ frac {1} {e}} \ aproximadamente 1,445}$

O requisito de a tetração ser holomórfica é importante por sua singularidade. Muitas funções S podem ser construídas como

${\ displaystyle S (z) = F \! \ left (~ z ~ + \ sum _ {n = 1} ^ {\ infty} \ sin (2 \ pi nz) ~ \ alpha _ {n} + \ sum _ {n = 1} ^ {\ infty} {\ Big (} 1- \ cos (2 \ pi nz) {\ Big)} ~ \ beta _ {n} \ right)}$

onde α e β são sequências reais que decaem rápido o suficiente para fornecer a convergência da série , pelo menos em valores moderados de Im  z .

A função S satisfaz as equações de tetração S ( z + 1) = exp ( S ( z )) , S (0) = 1 , e se α _n e β _{n se} aproximarem de 0 rápido o suficiente, será analítico em uma vizinhança do positivo eixo real. No entanto, se alguns elementos de { α } ou { β } não são zero, então a função S tem inúmeras singularidades e linhas de corte adicionais no plano complexo, devido ao crescimento exponencial de sen e cos ao longo do eixo imaginário; quanto menores são os coeficientes { α } e { β } , mais distantes essas singularidades estão do eixo real.

A extensão da tetração no plano complexo é, portanto, essencial para a singularidade; a tetração analítica real não é única.

Recursividade não elementar

Tetration (restrito a ) não é uma função recursiva elementar . Pode-se provar por indução que para cada função recursiva elementar f , existe uma constante c tal que ${\ displaystyle \ mathbb {N} ^ {2}}$

${\ displaystyle f (x) \ leq \ underbrace {2 ^ {2 ^ {\ cdot ^ {\ cdot ^ {x}}}}}} _ {c}.}$

Denotamos o lado direito ao lado . Suponha, ao contrário, que a tetração seja recursiva elementar. também é recursiva elementar. Pela desigualdade acima, existe uma constante c tal que . Ao deixar , temos isso , uma contradição. ${\ displaystyle g (c, x)}$${\ displaystyle g (x, x) +1}$${\ displaystyle g (x, x) +1 \ leq g (c, x)}$${\ displaystyle x = c}$${\ displaystyle g (c, c) +1 \ leq g (c, c)}$

Operações inversas

A exponenciação tem duas operações inversas; raízes e logaritmos . Analogamente, os inversos de tetração são muitas vezes chamado de super-raiz , e o super-logaritmo (Na verdade, todos os hiperoperação maior do que ou igual a 3 têm inversos análogos); por exemplo, na função , os dois inversos são a super-raiz cúbica de y e o superlogaritmo base  y de x . ${\ displaystyle {^ {3}} y = x}$

Super-root

A super-raiz é a operação inversa de tetração em relação à base: se , então y é uma n- ésima super-raiz de x ( ou ). ${\ displaystyle ^ {n} y = x}$${\ displaystyle {\ sqrt [{n}] {x}} _ {s}}$${\ displaystyle {\ sqrt [{n}] {x}} _ {4}}$

Por exemplo,

${\ displaystyle ^ {4} 2 = 2 ^ {2 ^ {2 ^ {2}}} = 65 {,} 536}$

então 2 é a 4ª super-raiz de 65.536.

Super-raiz quadrada

A 2ª ordem super-raiz , quadrada super-raiz , ou raiz quadrada de super tem duas notações equivalentes, e . É o inverso de e pode ser representado com a função Lambert W : ${\ displaystyle \ mathrm {ssrt} (x)}$${\ displaystyle {\ sqrt {x}} _ {s}}$${\ displaystyle ^ {2} x = x ^ {x}}$

${\ displaystyle \ mathrm {ssrt} (x) = e ^ {W (\ ln x)} = {\ frac {\ ln x} {W (\ ln x)}}}$

A função também ilustra a natureza reflexiva das funções raiz e logaritmo, pois a equação abaixo só é verdadeira quando : ${\ displaystyle y = \ mathrm {ssrt} (x)}$

${\ displaystyle {\ sqrt [{y}] {x}} = \ log _ {y} x}$

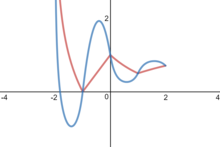
Como as raízes quadradas , a super-raiz quadrada de x pode não ter uma única solução. Ao contrário das raízes quadradas, determinar o número de super-raízes quadradas de x pode ser difícil. Em geral, se , então x tem duas super-raízes quadradas positivas entre 0 e 1; e se , então, x tem uma super-raiz quadrada positiva maior do que 1. Se x é positivo e menor do que não tem nenhuma super-raiz quadrada real , mas a fórmula dada acima produz contavelmente infinitamente muitos complexos para qualquer x finito diferente de 1. A função foi usada para determinar o tamanho dos clusters de dados . ${\ displaystyle e ^ {- 1 / e} <x <1}$${\ displaystyle x> 1}$${\ displaystyle e ^ {- 1 / e}}$

Em : ${\ displaystyle x = 1}$

${\ displaystyle \ mathrm {ssqrt} (x) = 1 + (x-1) - (x-1) ^ {2} + {\ frac {3} {2}} (x-1) ^ {3} - {\ frac {17} {6}} (x-1) ^ {4} + {\ frac {37} {6}} (x-1) ^ {5} - {\ frac {1759} {120}} (x-1) ^ {6} + {\ frac {13279} {360}} (x-1) ^ {7} + \ mathrm {O} \ left ((x-1) ^ {8} \ right) }$

Outras super-raízes

Para cada inteiro n > 2 , a função de ⁿ x é definido e aumentando para x ≥ 1 , e ⁿ 1 = 1 , de modo que o n ° de super-raiz de x , , existe para x ≥ 1 . ${\ displaystyle {\ sqrt [{n}] {x}} _ {s}}$

Uma das fórmulas mais simples e rápidas para uma super-raiz de terceiro grau é a fórmula recursiva, se: "x ^ x ^ x = a", e em seguida x (n + 1) = exp (W (W (x (n) ) * ln (a)))), por exemplo x (0) = 1.

No entanto, se a aproximação linear acima for usada, então se −1 < y ≤ 0 , então não pode existir. ${\ displaystyle ^ {y} x = y + 1}$${\ displaystyle ^ {y} {\ sqrt {y + 1}} _ {s}}$

Da mesma forma que a super-raiz quadrada, a terminologia para outras super-raízes pode ser baseada nas raízes normais : "super-raízes cúbicas" podem ser expressas como ; a "4ª super-raiz" pode ser expressa como ; eo " n º super-root" é . Note-se que não pode ser definido unicamente, porque pode haver mais do que um n ^th raiz. Por exemplo, x tem uma única super-raiz (real) se n for ímpar e até duas se n for par . ${\ displaystyle {\ sqrt [{3}] {x}} _ {s}}$${\ displaystyle {\ sqrt [{4}] {x}} _ {s}}$${\ displaystyle {\ sqrt [{n}] {x}} _ {s}}$${\ displaystyle {\ sqrt [{n}] {x}} _ {s}}$

Assim como com a extensão da tetração a alturas infinitas, a super-raiz pode ser estendida para n = ∞ , sendo bem definida se 1 / e ≤ x ≤ e . Observe isso e, portanto, isso . Portanto, quando está bem definida e, ao contrário da tetração normal, é uma função elementar . Por exemplo ,. ${\ displaystyle x = {^ {\ infty} y} = y ^ {\ left [^ {\ infty} y \ right]} = y ^ {x},}$${\ displaystyle y = x ^ {1 / x}}$${\ displaystyle {\ sqrt [{\ infty}] {x}} _ {s} = x ^ {1 / x}}$${\ displaystyle {\ sqrt [{\ infty}] {2}} _ {s} = 2 ^ {1/2} = {\ sqrt {2}}}$

Segue do teorema de Gelfond-Schneider que a super-raiz para qualquer inteiro positivo n é inteiro ou transcendental , e é inteiro ou irracional. Ainda é uma questão em aberto se as super-raízes irracionais são transcendentais no último caso. ${\ displaystyle {\ sqrt {n}} _ {s}}$${\ displaystyle {\ sqrt [{3}] {n}} _ {s}}$

Superlogaritmo

Uma vez que um contínuo aumento (em x definição) de tetração, ^x um , é seleccionado, o correspondente superlogaritmo ou é definida por todos os números reais x , e um > 1 . ${\ displaystyle \ operatorname {slog} _ {a} x}$${\ displaystyle \ log _ {a} ^ {4} x}$

A função slog _a  x satisfaz:

${\ displaystyle {\ begin {array} {lcl} \ operatorname {slog} _ {a} {^ {x} a} & = & x \\\ operatorname {slog} _ {a} a ^ {x} & = & 1+ \ operatorname {slog} _ {a} x \\\ operatorname {slog} _ {a} x & = & 1+ \ operatorname {slog} _ {a} \ log _ {a} x \\\ operatorname {slog} _ {a } x &> & - 2 \ end {array}}}$

Perguntas abertas

Além dos problemas com as extensões da tetração, existem várias questões em aberto sobre a tetração, particularmente no que diz respeito às relações entre sistemas numéricos, como números inteiros e números irracionais :

• Não se sabe se existe um inteiro positivo n para o qual ⁿ π ou ⁿ e é um inteiro. Em particular, não se sabe se ⁴ π ou ⁵ e é um número inteiro.
• Não se sabe se ⁿ q é um número inteiro para qualquer número inteiro positivo n e q racional não inteiro positivo . Por exemplo, não se sabe se a raiz positiva da equação ⁴ x = 2 é um número racional.

Veja também

• Função Ackermann
• Notação Big O
• Função exponencial dupla
• Hiperoperação
• Logaritmo iterado
• Aritmética de índice de nível simétrico

Notas

Referências

• Daniel Geisler, Tetration
• Ioannis Galidakis, Sobre a extensão de hyper4 a não inteiros (sem data, 2006 ou anterior) (uma revisão mais simples e fácil de ler da próxima referência)
• Ioannis Galidakis, On Extending hyper4 e Knuth's Up-arrow Notation to the Reals (sem data, 2006 ou anterior).
• Robert Munafo, Extension of the hyper4 function to reals (Uma discussão informal sobre como estender a tetração aos números reais.)
• Lode Vandevenne, Tetration of the Square Root of Two . (2004). (Tente estender a tetração para números reais.)
• Ioannis Galidakis, Mathematics , (lista definitiva de referências à pesquisa de tetração. Muitas informações sobre a função Lambert W, superfícies de Riemann e continuação analítica.)
• Joseph MacDonell, Alguns pontos críticos da função de hiperpotência .
• Dave L. Renfro, páginas da Web para exponenciais infinitamente iteradas
• Knobel, R. (1981). "Exponenciais reiterados". American Mathematical Monthly . 88 (4): 235–252. doi : 10.1080 / 00029890.1981.11995239 .
• Hans Maurer, "Über die Funktion für ganzzahliges Argument (Abundanzen)." Mittheilungen der Mathematische Gesellschaft em Hamburgo 4 , (1901), p. 33–50. (Referência ao uso do artigo de Knobel.)${\ displaystyle y = x ^ {[x ^ {[x (\ cdots)]}]}}$ ${\ displaystyle \ {^ {n} a}}$
• A Quarta Operação
• Luca Moroni, As estranhas propriedades da torre de energia infinita ( https://arxiv.org/abs/1908.05559 )

Leitura adicional

• Galidakis, Ioannis; Weisstein, Eric Wolfgang . "Torre de energia" . MathWorld . Página visitada em 05/07/2019 .