Angulo solido - Solid angle

Angulo solido
Símbolos comuns	Ω
Unidade SI	Steradian
Outras unidades	Grau quadrado
Em unidades de base SI	m 2 / m 2
Conservado ?	Não
Derivações de outras quantidades	${\ displaystyle \ Omega = A / r ^ {2}}$
Dimensão	${\ displaystyle 1}$

Em geometria , um ângulo sólido (símbolo: Ω ) é uma medida da quantidade do campo de visão de algum ponto específico que um determinado objeto cobre. Ou seja, é uma medida de quão grande o objeto parece para um observador olhando daquele ponto. O ponto a partir do qual o objeto é visto é chamado de vértice do ângulo sólido, e diz-se que o objeto subtende seu ângulo sólido a partir desse ponto.

No Sistema Internacional de Unidades (SI), um ângulo sólido é expresso em uma unidade adimensional chamada esteradiana (símbolo: sr). Um esteradiano corresponde a uma unidade de área na esfera unitária ao redor do ápice, então um objeto que bloqueia todos os raios do ápice cobriria um número de esteradianos igual à área total da superfície da esfera unitária ,. Os ângulos sólidos também podem ser medidos em quadrados de medidas angulares, como graus , minutos e segundos. ${\ displaystyle 4 \ pi}$

Um pequeno objeto próximo pode subtender o mesmo ângulo sólido de um objeto maior mais distante. Por exemplo, embora a Lua seja muito menor que o Sol , também está muito mais perto da Terra . Na verdade, visto de qualquer ponto da Terra, ambos os objetos têm aproximadamente o mesmo ângulo sólido, bem como tamanho aparente. Isso é evidente durante um eclipse solar .

Definição e propriedades

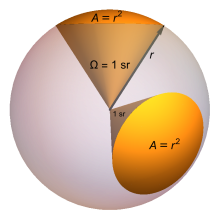
O ângulo sólido de um objeto em esteradianos é igual à área do segmento de uma esfera unitária , centrada no vértice, que o objeto cobre. Um ângulo sólido em esteradianos é igual à área de um segmento de uma esfera unitária da mesma forma que um ângulo plano em radianos é igual ao comprimento de um arco de um círculo unitário ; portanto, assim como um ângulo plano em radianos é a razão entre o comprimento de um arco circular e seu raio, um ângulo sólido em estereadianos é a seguinte razão:

${\ displaystyle \ Omega = {\ frac {A} {r ^ {2}}}}$

onde A é a área da superfície esférica er é o raio da esfera considerada.

Os ângulos sólidos são freqüentemente usados ​​na astronomia , física e, em particular, na astrofísica . O ângulo sólido de um objeto que está muito longe é aproximadamente proporcional à razão entre a área e a distância ao quadrado. Aqui, "área" significa a área do objeto quando projetado ao longo da direção de visualização.

Qualquer área em uma esfera que seja igual em área ao quadrado de seu raio, quando observada de seu centro, subtende precisamente um esteradiano .

O ângulo sólido de uma esfera medido de qualquer ponto em seu interior é 4 π  sr, e o ângulo sólido subtendido no centro de um cubo por uma de suas faces é um sexto disso, ou2 π/3 sr. Ângulos sólidos também podem ser medidos em graus quadrados (1 sr = (180/π) ² graus quadrados), em minutos quadrados e segundos quadrados, ou em frações da esfera (1 sr =1/4 πárea fracionária), também conhecida como spat (1 sp = 4 π  sr).

Em coordenadas esféricas, existe uma fórmula para o diferencial ,

${\ displaystyle d \ Omega = \ sin \ theta \, d \ theta \, d \ varphi}$

onde θ é a colatitude (ângulo do Pólo Norte) e φ é a longitude.

O ângulo sólido para uma superfície orientada arbitrária S subtendida em um ponto P é igual ao ângulo sólido da projeção da superfície S para a esfera unitária com centro P , que pode ser calculada como a integral da superfície :

${\ displaystyle \ Omega = \ iint _ {S} {\ frac {{\ hat {r}} \ cdot {\ hat {n}}} {r ^ {2}}} \, dS \ = \ iint _ { S} \ sin \ theta \, d \ theta \, d \ varphi}$

onde é o vetor unitário correspondente a , o vetor posição de uma área infinitesimal da superfície dS em relação ao ponto P , e onde representa o vetor normal unitário para dS . Mesmo que a projeção da esfera unitária para a superfície S não seja isomórfica , as múltiplas dobras são corretamente consideradas de acordo com a orientação da superfície descrita pelo sinal do produto escalar . ${\ displaystyle {\ hat {r}} = {\ vec {r}} / r}$${\ displaystyle {\ vec {r}}}$${\ displaystyle {\ hat {n}}}$ ${\ displaystyle {\ hat {r}} \ cdot {\ hat {n}}}$

Assim, pode-se aproximar o ângulo sólido subtendido por uma pequena faceta com área de superfície plana dS , orientação e distância r do observador como: ${\ displaystyle {\ hat {n}}}$

${\ displaystyle d \ Omega = 4 \ pi \ left ({\ frac {dS} {A}} \ right) \, ({\ hat {r}} \ cdot {\ hat {n}})}$

onde a área da superfície de uma esfera é A = 4 π r ² .

Aplicações práticas

• Definindo a intensidade luminosa e luminância , e as quantidades radiométricas correspondentes, intensidade radiante e radiância
• Calculando o excesso esférico E de um triângulo esférico
• O cálculo de potenciais usando o método dos elementos de fronteira (BEM)
• Avaliando o tamanho dos ligantes em complexos metálicos, consulte o ângulo do cone do ligante
• Calculando o campo elétrico e a força do campo magnético em torno das distribuições de carga
• Derivando a Lei de Gauss
• Calculando a potência emissiva e irradiação na transferência de calor
• Calculando seções transversais no espalhamento de Rutherford
• Calculando seções transversais em espalhamento Raman
• O ângulo sólido do cone de aceitação da fibra óptica

Ângulos sólidos para objetos comuns

Cone, tampa esférica, hemisfério

Seção do cone (1) e tampa esférica (2) dentro de uma esfera. Nesta figura θ = A / 2 e r = 1 .

O ângulo sólido de um cone com seu ápice no ápice do ângulo sólido, e com ângulo de vértice 2 θ , é a área de uma tampa esférica em uma esfera unitária

$${\ displaystyle \ Omega = 2 \ pi \ left (1- \ cos \ theta \ right) \ = 4 \ pi \ sin ^ {2} {\ frac {\ theta} {2}}.}$$

Para pequenas θ tal que cos θ ≈ 1 - θ ² /2 , isto reduz a área de um círculo ¸ θ ² .

O acima é encontrado calculando a seguinte integral dupla usando o elemento de superfície da unidade em coordenadas esféricas :

$${\ displaystyle \ int _ {0} ^ {2 \ pi} \ int _ {0} ^ {\ theta} \ sin \ theta '\, d \ theta' \, d \ phi = \ int _ {0} ^ {2 \ pi} d \ phi \ int _ {0} ^ {\ theta} \ sin \ theta '\, d \ theta' =}$$

$${\ displaystyle \ qquad 2 \ pi \ int _ {0} ^ {\ theta} \ sin \ theta '\, d \ theta' = 2 \ pi \ left [- \ cos \ theta '\ right] _ {0} ^ {\ theta} \ = 2 \ pi \ left (1- \ cos \ theta \ right).}$$

Esta fórmula também pode ser derivada sem o uso de cálculos . Mais de 2.200 anos atrás, Arquimedes provou que a área da superfície de uma capa esférica é sempre igual à área de um círculo cujo raio é igual à distância da borda da capa esférica ao ponto onde o eixo de simetria da capa intercepta a capa. No diagrama, este raio é dado como

$${\ displaystyle 2r \ sin {\ frac {\ theta} {2}}.}$$

Portanto, para uma esfera unitária, o ângulo sólido da tampa esférica é dado como

$${\ displaystyle \ Omega = 4 \ pi \ sin ^ {2} {\ frac {\ theta} {2}} = 2 \ pi \ left (1- \ cos \ theta \ right).}$$

Quando θ =π/2, a tampa esférica torna-se um hemisfério com um ângulo sólido 2 π .

O ângulo sólido do complemento do cone é

$${\ displaystyle 4 \ pi - \ Omega = 2 \ pi \ left (1+ \ cos \ theta \ right) = 4 \ pi \ cos ^ {2} {\ frac {\ theta} {2}}.}$$

Este também é o ângulo sólido da parte da esfera celeste que um observador astronômico posicionado na latitude θ pode ver enquanto a Terra gira. No equador, toda a esfera celeste é visível; em qualquer um dos pólos, apenas uma metade.

O ângulo sólido subtendido por um segmento de uma tampa esférica cortado por um plano no ângulo γ do eixo do cone e passando pelo ápice do cone pode ser calculado pela fórmula

$${\ displaystyle \ Omega = 2 \ left [\ arccos \ left ({\ frac {\ sin \ gamma} {\ sin \ theta}} \ right) - \ cos \ theta \ arccos \ left ({\ frac {\ tan \ gamma} {\ tan \ theta}} \ right) \ right].}$$

Por exemplo, se γ = - θ , então a fórmula se reduz à fórmula do limite esférico acima: o primeiro termo torna-se π , e o segundo π cos θ .

Tetraedro

Deixe OABC ser os vértices de um tetraedro com uma origem em O subtendido pelo ABC face triangular, onde são as posições do vector dos vértices A, B e C. Definir o ângulo do vértice θ _um a ser o BOC ângulo e definir θ _b , θ _c correspondentemente. Let Ser o ângulo diedro entre os planos que contêm as faces tetraédricas OAC e OBC e definir , correspondentemente. O ângulo sólido Ω subtendido pela superfície triangular ABC é dado por ${\ displaystyle {\ vec {a}} \, \, {\ vec {b}} \, \, {\ vec {c}}}$ ${\ displaystyle \ phi _ {ab}}$${\ displaystyle \ phi _ {ac}}$${\ displaystyle \ phi _ {bc}}$

${\ displaystyle \ Omega = \ left (\ phi _ {ab} + \ phi _ {bc} + \ phi _ {ac} \ right) \ - \ pi \}$

Isso decorre da teoria do excesso esférico e leva ao fato de que há um teorema análogo ao teorema de que "A soma dos ângulos internos de um triângulo plano é igual a π " , para a soma dos quatro ângulos sólidos internos de um tetraedro da seguinte forma:

${\ displaystyle \ sum _ {i = 1} ^ {4} \ Omega _ {i} = 2 \ sum _ {i = 1} ^ {6} \ phi _ {i} \ -4 \ pi \}$

onde varia em todos os seis ângulos diédricos entre quaisquer dois planos que contêm as faces tetraédricas OAB, OAC, OBC e ABC. ${\ displaystyle \ phi _ {i}}$

Uma fórmula útil para calcular o ângulo sólido do tetraedro na origem O que é puramente uma função dos ângulos do vértice θ _a , θ _b , θ _c é dada pelo teorema de L'Huilier como

${\ displaystyle \ tan \ left ({\ frac {1} {4}} \ Omega \ right) = {\ sqrt {\ tan \ left ({\ frac {\ theta _ {s}} {2}} \ right ) \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {a}} {2}} \ right) \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {b}} {2}} \ right) \ tan \ left ({\ frac {\ theta _ {s} - \ theta _ {c}} {2}} \ right)}}}$

Onde

${\ displaystyle \ theta _ {s} = {\ frac {\ theta _ {a} + \ theta _ {b} + \ theta _ {c}} {2}}}$.

Outra fórmula interessante envolve expressar os vértices como vetores no espaço tridimensional. Sejam as posições vetoriais dos vértices A, B e C, e sejam a , b e c a magnitude de cada vetor (a distância do ponto de origem). O ângulo sólido Ω subtendido pela superfície triangular ABC é: ${\ displaystyle {\ vec {a}} \, \, {\ vec {b}} \, \, {\ vec {c}}}$

${\ displaystyle \ tan \ left ({\ frac {1} {2}} \ Omega \ right) = {\ frac {\ left | {\ vec {a}} \ {\ vec {b}} \ {\ vec {c}} \ right |} {abc + \ left ({\ vec {a}} \ cdot {\ vec {b}} \ right) c + \ left ({\ vec {a}} \ cdot {\ vec {c }} \ right) b + \ left ({\ vec {b}} \ cdot {\ vec {c}} \ right) a}}}$

Onde

${\ displaystyle \ left | {\ vec {a}} \ {\ vec {b}} \ {\ vec {c}} \ right | = {\ vec {a}} \ cdot ({\ vec {b}} \ times {\ vec {c}})}$

denota o produto escalar triplo dos três vetores e denota o produto escalar . ${\ displaystyle {\ vec {a}} \ cdot {\ vec {b}}}$

Deve-se ter cuidado aqui para evitar ângulos sólidos negativos ou incorretos. Uma fonte de erros potenciais é que o produto triplo escalar pode ser negativo se a , b , c tiverem o enrolamento errado . Computação é uma solução suficiente, uma vez que nenhuma outra parte da equação depende do enrolamento. A outra armadilha surge quando o produto triplo escalar é positivo, mas o divisor é negativo. Neste caso, retorna um valor negativo que deve ser aumentado em π .

Pirâmide

O ângulo sólido de uma pirâmide retangular direita de quatro lados com ângulos de vértice a e b ( ângulos diédricos medidos nas faces laterais opostas da pirâmide) é

${\ displaystyle \ Omega = 4 \ arcsin \ left (\ sin \ left ({a \ over 2} \ right) \ sin \ left ({b \ over 2} \ right) \ right)}$

Se ambos os comprimentos laterais ( α e β ) da base da pirâmide e a distância ( d ) do centro do retângulo da base ao ápice da pirâmide (o centro da esfera) são conhecidos, a equação acima pode ser manipulado para dar

${\ displaystyle \ Omega = 4 \ arctan {\ frac {\ alpha \ beta} {2d {\ sqrt {4d ^ {2} + \ alpha ^ {2} + \ beta ^ {2}}}}}}$

O ângulo sólido de uma pirâmide n- diagonal direita , em que a base da pirâmide é um polígono regular de n lados do perímetro r , com uma altura da pirâmide h é

${\ displaystyle \ Omega = 2 \ pi -2n \ arctan \ left ({\ frac {\ tan \ left ({\ pi \ over n} \ right)} {\ sqrt {1+ {r ^ {2} \ over h ^ {2}}}}} \ right)}$

O ângulo sólido de uma pirâmide arbitrária com uma base de n lados definida pela sequência de vetores unitários que representam as arestas { s ₁ , s ₂ }, ... s _n pode ser eficientemente calculado por:

${\ displaystyle \ Omega = 2 \ pi - \ arg \ prod _ {j = 1} ^ {n} \ left (\ left (s_ {j-1} s_ {j} \ right) \ left (s_ {j} s_ {j + 1} \ right) - \ left (s_ {j-1} s_ {j + 1} \ right) + i \ left [s_ {j-1} s_ {j} s_ {j + 1} \ certo, certo)}$

onde parênteses (* *) é um produto escalar e colchetes [* * *] é um produto escalar tripla , e i é uma unidade imaginária . Os índices são alternados: s ₀ = s _n e s ₁ = s _{n + 1} .

Retângulo latitude-longitude

O ângulo sólido de um retângulo de latitude-longitude em um globo é

${\ displaystyle \ left (\ sin \ phi _ {\ mathrm {N}} - \ sin \ phi _ {\ mathrm {S}} \ right) \ left (\ theta _ {\ mathrm {E}} - \ theta _ {\ mathrm {W}} \, \! \ direita) \; \ mathrm {sr}}$,

onde φ _N e φ _S são as linhas de latitude norte e sul (medidas a partir do equador em radianos com o ângulo aumentando para o norte), e θ _E e θ _W são as linhas de longitude leste e oeste (onde o ângulo em radianos aumenta para o leste). Matematicamente, isso representa um arco de ângulo ϕ _N - ϕ _S varrido em torno de uma esfera por θ _E - θ _W radianos. Quando a longitude se estende por 2 π radianos e a latitude se estende por π radianos, o ângulo sólido é o de uma esfera.

Um retângulo de latitude-longitude não deve ser confundido com o ângulo sólido de uma pirâmide retangular. Todos os quatro lados de uma pirâmide retangular cruzam a superfície da esfera em grandes arcos de círculo . Com um retângulo latitude-longitude, apenas as linhas de longitude são grandes arcos de círculo; linhas de latitude não são.

Objetos Celestiais

Usando a definição de diâmetro angular , a fórmula para o ângulo sólido de um objeto celeste pode ser definida em termos do raio do objeto,, e a distância do observador ao objeto ,: ${\ textstyle R}$${\ displaystyle d}$

${\ displaystyle \ Omega = 2 \ pi \ left (1 - {\ frac {\ sqrt {d ^ {2} -R ^ {2}}} {d}} \ right): d \ geq R}$

Ao inserir os valores médios apropriados para o Sol e a Lua (em relação à Terra), o ângulo sólido médio do Sol é 6,794 × 10 ^{- 5} esteradianos e o ângulo sólido médio da Lua é 6,418 × 10 ^{- 5} esteradianos. Em termos da esfera celeste total, o Sol e a Lua subtendem áreas fracionárias médias de 0,0005406% (5,406 ppm ) e 0,0005107% (5,107 ppm), respectivamente. Como esses ângulos sólidos têm aproximadamente o mesmo tamanho, a Lua pode causar eclipses solares totais e anulares, dependendo da distância entre a Terra e a Lua durante o eclipse.

Ângulos sólidos em dimensões arbitrárias

O ângulo sólido subtendido pela superfície esférica completa ( d - 1 ) -dimensional da esfera unitária no espaço euclidiano d- dimensional pode ser definido em qualquer número de dimensões d . Freqüentemente, é necessário esse fator de ângulo sólido em cálculos com simetria esférica. É dado pela fórmula

${\ displaystyle \ Omega _ {d} = {\ frac {2 \ pi ^ {\ frac {d} {2}}} {\ Gamma \ left ({\ frac {d} {2}} \ right)}} \}$

onde Γ é a função gama . Quando d é um número inteiro, a função gama pode ser calculada explicitamente. Segue que

${\ displaystyle \ Omega _ {d} = {\ begin {cases} {\ frac {1} {\ left ({\ frac {d} {2}} - 1 \ right)!}} 2 \ pi ^ {\ frac {d} {2}} \ & d {\ text {even}} \\ {\ frac {\ left ({\ frac {1} {2}} \ left (d-1 \ right) \ right)!} {(d-1)!}} 2 ^ {d} \ pi ^ {{\ frac {1} {2}} (d-1)} \ & d {\ text {ímpar}} \ end {casos}}}$

Isso dá os resultados esperados de 4 π esteradianos para a esfera 3D limitada por uma superfície de área 4π r ² e 2 π radianos para o círculo 2D limitado por uma circunferência de comprimento 2π r . Ele também fornece o 2 ligeiramente menos óbvio para o caso 1D, no qual a "esfera" centrada na origem 1D é o intervalo [- r , r ] e este é limitado por dois pontos limites.

A contraparte da fórmula vetorial em dimensão arbitrária foi derivada por Aomoto e independentemente por Ribando. Ele os expressa como uma série multivariada de Taylor infinita:

${\ displaystyle \ Omega = \ Omega _ {d} {\ frac {| \ operatorname {det} (V) |} {(4 \ pi) ^ {d / 2}}} \ sum _ {{\ vec {a }} \ in \ mathbb {N} ^ {\ binom {d} {2}}} \ left [{\ frac {(-2) ^ {\ sum _ {i <j} a_ {ij}}} {\ prod _ {i <j} a_ {ij}!}} \ prod _ {i} \ Gamma \ left ({\ frac {1+ \ sum _ {m \ neq i} a_ {im}} {2}} \ direita) \ right] {\ vec {\ alpha}} ^ {\ vec {a}}.}$

Dados d vetores unitários que definem o ângulo, deixe V denotar a matriz formada combinando-os de forma que a i- ésima coluna seja , e . As variáveis formam uma multivariável . Para um "congruente" multiexponent inteiro definimos . A notação para significa a variável , da mesma forma para os expoentes . Conseqüentemente, o termo significa a soma de todos os termos em que l aparece como o primeiro ou o segundo índice. Onde esta série converge, ela converge para o ângulo sólido definido pelos vetores. ${\ displaystyle {\ vec {v_ {i}}}}$${\ displaystyle {\ vec {v_ {i}}}}$${\ displaystyle \ alpha _ {ij} = {\ vec {v_ {i}}} \ cdot {\ vec {v_ {j}}} = \ alpha _ {ji}, \ alpha _ {ii} = 1}$${\ displaystyle \ alpha _ {ij}, 1 \ leq i <j \ leq d}$${\ displaystyle {\ vec {\ alpha}} = (\ alpha _ {12}, \ dotsc, \ alpha _ {1d}, \ alpha _ {23}, \ dotsc, \ alpha _ {d-1, d} ) \ in \ mathbb {R} ^ {\ binom {d} {2}}}$${\ displaystyle {\ vec {a}} = (a_ {12}, \ dotsc, a_ {1d}, a_ {23}, \ dotsc, a_ {d-1, d}) \ in \ mathbb {N} ^ {\ binom {d} {2}}}$${\ displaystyle {\ vec {\ alpha}} ^ {\ vec {a}} = \ prod \ alpha _ {ij} ^ {a_ {ij}}}$${\ displaystyle \ alpha _ {ji}}$${\ displaystyle j> i}$${\ displaystyle \ alpha _ {ij}}$${\ displaystyle a_ {ji}}$${\ displaystyle \ sum _ {m \ neq l} a_ {lm}}$${\ displaystyle {\ vec {a}}}$

Referências

Leitura adicional

• Jaffey, AH (1954). "Ângulo sólido subtendido por uma abertura circular em fontes pontuais e dispersas: fórmulas e algumas tabelas". Rev. Sci. Instrum . 25 . pp. 349–354. Bibcode : 1954RScI ... 25..349J . doi : 10.1063 / 1.1771061 .
• Masket, A. Victor (1957). "Integrais de contorno de ângulo sólido, séries e tabelas". Rev. Sci. Instrum . 28 (3). p. 191. bibcode : 1957RScI ... 28..191M . doi : 10.1063 / 1.1746479 .
• Naito, Minoru (1957). "Um método de cálculo do ângulo sólido subtendido por uma abertura circular". J. Phys. Soc. Jpn . 12 (10). pp. 1122–1129. Bibcode : 1957JPSJ ... 12.1122N . doi : 10.1143 / JPSJ.12.1122 .
• Paxton, F. (1959). "Cálculo do ângulo sólido para um disco circular". Rev. Sci. Instrum . 30 (4). p. 254. bibcode : 1959RScI ... 30..254P . doi : 10.1063 / 1.1716590 .
• Gardner, RP; Carnesale, A. (1969). “O ângulo sólido subtendido em um ponto por um disco circular”. Nucl. Instrum. Métodos . 73 (2). pp. 228–230. Bibcode : 1969NucIM..73..228G . doi : 10.1016 / 0029-554X (69) 90214-6 .
• Gardner, RP; Verghese, K. (1971). "No ângulo sólido subtendido por um disco circular". Nucl. Instrum. Métodos . 93 (1). pp. 163–167. Bibcode : 1971NucIM..93..163G . doi : 10.1016 / 0029-554X (71) 90155-8 .
• Asvestas, John S ..; Englund, David C. (1994). "Calculando o ângulo sólido subtendido por uma figura plana". Optar. Eng . 33 (12). pp. 4055–4059. Bibcode : 1994OptEn..33.4055A . doi : 10.1117 / 12.183402 .
• Tryka, Stanislaw (1997). "Distribuição angular do ângulo sólido em um ponto subtendido por um disco circular". Optar. Comun . 137 (4–6). pp. 317–333. Bibcode : 1997OptCo.137..317T . doi : 10.1016 / S0030-4018 (96) 00789-4 .
• Prata, MJ (2004). "Cálculo analítico do ângulo sólido subtendido por um detector de disco circular em uma fonte cosseno pontual". Nucl. Instrum. Methods Phys. Res. Um . 521 . p. 576. arXiv : math-ph / 0305034 . Bibcode : 2004NIMPA.521..576P . doi : 10.1016 / j.nima.2003.10.098 .
• Timus, DM; Prata, MJ; Kalla, SL; Abbas, MI; Oner, F .; Galiano, E. (2007). "Alguns resultados analíticos adicionais sobre o ângulo sólido subtendido em um ponto por um disco circular usando integrais elípticas". Nucl. Instrum. Methods Phys. Res. Um . 580 . pp. 149-152. Bibcode : 2007NIMPA.580..149T . doi : 10.1016 / j.nima.2007.05.055 .

links externos

• Teoria do polígono do HCR (ângulo sólido subtendido por qualquer polígono) de Academia.edu
• Arthur P. Norton, A Star Atlas, Gall and Inglis, Edimburgo, 1969.
• MG Kendall, A Course in the Geometry of N Dimensions, No. 8 of Griffin's Statistical Monographs & Courses, ed. MG Kendall, Charles Griffin & Co. Ltd, Londres, 1961
• Weisstein, Eric W. "Solid Angle" . MathWorld .