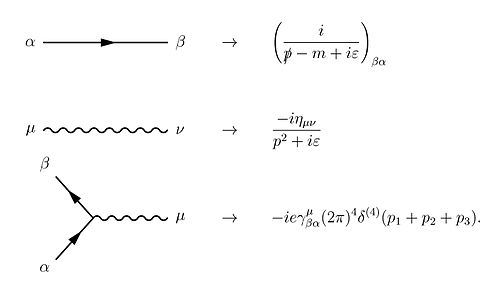Eletrodinâmica quântica - Quantum electrodynamics

Teoria quântica de campos
Diagrama de Feynman
História
Fundo Teoria de campo Eletromagnetismo Força fraca Força forte Mecânica quântica Relatividade especial Relatividade geral Teoria de calibre
Simetrias Simetria em mecânica quântica Simetria C Simetria P Simetria T Simetria de translação espacial Simetria de tradução de tempo Simetria de rotação Simetria de Lorentz Simetria de Poincaré Simetria de calibre Quebra de simetria explícita Quebra espontânea de simetria Teoria de Yang-Mills Carga Noether Carga topológica
Ferramentas Anomalia Cruzando Teoria de campo eficaz Valor de expectativa Fantasmas Faddeev-Popov Diagrama de Feynman Teoria de calibre reticulado Fórmula de redução LSZ Função de partição Propagator Quantização Regularização Renormalização Estado de vácuo Teorema de Wick Axiomas de Wightman
Equações Equação de Dirac Equação de Klein-Gordon Equações de Proca Equação de Wheeler-DeWitt Equações de Bargmann-Wigner
Modelo Padrão Eletrodinâmica quântica Interação eletrofraca Cromodinâmica quântica Mecanismo de Higgs
Teorias incompletas Teoria de campo quântico topológico Teoria das cordas Supersimetria Technicolor Teoria de tudo Gravidade quântica
Cientistas CD Anderson PW Anderson Bethe Bjorken Bogoliubov Brout Callan Coleman DeWitt Dirac Dyson Englert Fermi Feynman Fierz Fock Fröhlich Brilho Gell-Mann Bruto Guralnik Heisenberg Higgs Haag Hagen 't Hooft Jordânia Kendall Kibble Cordeiro Landau Lee Majorana Mills Nambu Nishijima Parisi Polyakov Salam Schwinger Skyrme Sudarshan Tomonaga Veltman ala Weinberg Weisskopf Weyl Wilczek Wilson Yang Yukawa
v t e

Na física de partículas , a eletrodinâmica quântica ( QED ) é a teoria quântica de campo relativística da eletrodinâmica . Em essência, ele descreve como a luz e a matéria interagem e é a primeira teoria em que um acordo completo entre a mecânica quântica e a relatividade especial é alcançado. O QED descreve matematicamente todos os fenômenos que envolvem partículas eletricamente carregadas interagindo por meio da troca de fótons e representa a contraparte quântica do eletromagnetismo clássico, fornecendo uma descrição completa da interação entre matéria e luz.

Em termos técnicos, QED pode ser descrito como uma teoria de perturbação do vácuo quântico eletromagnético . Richard Feynman a chamou de "a joia da física" por suas previsões extremamente precisas de quantidades como o momento magnético anômalo do elétron e a mudança de Lamb dos níveis de energia do hidrogênio .

História

Paul Dirac

A primeira formulação de uma teoria quântica que descreve a radiação e a interação da matéria é atribuída ao cientista britânico Paul Dirac , que (durante a década de 1920) foi capaz de calcular o coeficiente de emissão espontânea de um átomo .

Dirac descreveu a quantização do campo eletromagnético como um conjunto de osciladores harmônicos com a introdução do conceito de operadores de criação e aniquilação de partículas. Nos anos seguintes, com contribuições de Wolfgang Pauli , Eugene Wigner , Pascual Jordan , Werner Heisenberg e uma elegante formulação da eletrodinâmica quântica de Enrico Fermi , os físicos passaram a acreditar que, em princípio, seria possível realizar qualquer cálculo para qualquer processo físico envolvendo fótons e partículas carregadas. No entanto, estudos posteriores de Felix Bloch com Arnold Nordsieck e Victor Weisskopf , em 1937 e 1939, revelaram que tais cálculos eram confiáveis ​​apenas na teoria de perturbação de primeira ordem , um problema já apontado por Robert Oppenheimer . Em ordens superiores na série, infinitos emergiram, tornando tais cálculos sem sentido e lançando sérias dúvidas sobre a consistência interna da própria teoria. Sem solução para este problema conhecida na época, parecia que existia uma incompatibilidade fundamental entre a relatividade especial e a mecânica quântica .

Hans Bethe

As dificuldades com a teoria aumentaram até o final da década de 1940. Os aprimoramentos na tecnologia de microondas tornaram possível fazer medições mais precisas do deslocamento dos níveis de um átomo de hidrogênio , agora conhecido como deslocamento de Lamb e momento magnético do elétron. Esses experimentos expuseram discrepâncias que a teoria não foi capaz de explicar.

Uma primeira indicação de uma possível saída foi dada por Hans Bethe em 1947, após participar da Shelter Island Conference . Enquanto viajava de trem da conferência para Schenectady, ele fez o primeiro cálculo não relativístico da mudança das linhas do átomo de hidrogênio medida por Lamb e Retherford . Apesar das limitações do cálculo, a concordância foi excelente. A ideia era simplesmente anexar infinitos a correções de massa e carga que foram realmente fixadas em um valor finito por experimentos. Dessa forma, os infinitos são absorvidos por essas constantes e geram um resultado finito em boa concordância com os experimentos. Este procedimento foi denominado renormalização .

Feynman (centro) e Oppenheimer (direita) em Los Alamos .

Com base na intuição de Bethe e nos artigos fundamentais sobre o assunto de Shin'ichirō Tomonaga , Julian Schwinger , Richard Feynman e Freeman Dyson , foi finalmente possível obter formulações covariantes completas que eram finitas em qualquer ordem em uma série de perturbações da eletrodinâmica quântica. Shin'ichirō Tomonaga, Julian Schwinger e Richard Feynman foram agraciados com o Prêmio Nobel de Física de 1965 por seu trabalho nesta área. Suas contribuições, e as de Freeman Dyson , foram sobre formulações covariantes e invariantes de calibre da eletrodinâmica quântica que permitem cálculos de observáveis ​​em qualquer ordem da teoria de perturbação . A técnica matemática de Feynman, baseada em seus diagramas , inicialmente parecia muito diferente da abordagem teórica de campo baseada no operador de Schwinger e Tomonaga, mas Freeman Dyson mais tarde mostrou que as duas abordagens eram equivalentes. A renormalização , a necessidade de atribuir um significado físico a certas divergências que aparecem na teoria por meio de integrais , tornou-se subsequentemente um dos aspectos fundamentais da teoria quântica de campos e passou a ser vista como um critério para a aceitabilidade geral de uma teoria. Mesmo que a renormalização funcione muito bem na prática, Feynman nunca se sentiu totalmente confortável com sua validade matemática, mesmo se referindo à renormalização como um "jogo de concha" e "hocus pocus".

QED serviu como modelo e gabarito para todas as teorias quânticas de campo subsequentes. Uma dessas teorias subsequentes é a cromodinâmica quântica , que começou no início dos anos 1960 e atingiu sua forma atual no trabalho dos anos 1970 de H. David Politzer , Sidney Coleman , David Gross e Frank Wilczek . Com base no trabalho pioneiro de Schwinger , Gerald Guralnik , Dick Hagen e Tom Kibble , Peter Higgs , Jeffrey Goldstone e outros, Sheldon Lee Glashow , Steven Weinberg e Abdus Salam mostraram independentemente como a força nuclear fraca e a eletrodinâmica quântica poderiam ser fundidas em uma única força eletrofraca .

A visão de Feynman da eletrodinâmica quântica

Introdução

Perto do fim de sua vida, Richard Feynman deu uma série de palestras sobre QED destinadas ao público leigo. Essas palestras foram transcritas e publicadas como Feynman (1985), QED: The Strange Theory of Light and Matter , uma exposição não matemática clássica de QED do ponto de vista articulado abaixo.

Os principais componentes da apresentação de Feynman do QED são três ações básicas.

Um fóton vai de um lugar e hora para outro lugar e hora.

Um elétron vai de um lugar e tempo para outro lugar e tempo.

Um elétron emite ou absorve um fóton em um determinado lugar e hora.

Elementos do diagrama de Feynman

Essas ações são representadas na forma de taquigrafia visual pelos três elementos básicos dos diagramas de Feynman : uma linha ondulada para o fóton, uma linha reta para o elétron e uma junção de duas linhas retas e uma ondulada para um vértice que representa a emissão ou absorção. de um fóton por um elétron. Tudo isso pode ser visto no diagrama ao lado.

Além da abreviatura visual para as ações, Feynman introduz outro tipo de abreviatura para as quantidades numéricas chamadas amplitudes de probabilidade . A probabilidade é o quadrado do valor absoluto da amplitude de probabilidade total ,. Se um fóton se move de um lugar e tempo para outro lugar e tempo , a quantidade associada é escrita na taquigrafia de Feynman como . A quantidade semelhante para um elétron movendo-se de para é escrita . A quantidade que nos diz sobre a amplitude de probabilidade de emissão ou absorção de um fóton que ele chama de j . Isso está relacionado, mas não é o mesmo que, a carga do elétron medida e . ${\displaystyle {\text{probability}}=|f({\text{amplitude}})|^{2}}$${\displaystyle A}$${\displaystyle B}$${\displaystyle P(A{\text{ to }}B)}$${\displaystyle C}$${\displaystyle D}$${\displaystyle E(C{\text{ to }}D)}$

O QED é baseado na suposição de que as interações complexas de muitos elétrons e fótons podem ser representadas pelo ajuste de uma coleção adequada dos três blocos de construção acima e, em seguida, usando as amplitudes de probabilidade para calcular a probabilidade de qualquer interação complexa. Acontece que a ideia básica de QED pode ser comunicada assumindo que o quadrado do total das amplitudes de probabilidade mencionadas acima ( P ( A para B ), E ( C para D ) ej ) atua exatamente como nossa probabilidade diária ( uma simplificação feita no livro de Feynman). Mais tarde, isso será corrigido para incluir especificamente a matemática do estilo quântico, seguindo Feynman.

As regras básicas de amplitudes de probabilidade que serão utilizadas são:

Construções básicas

Suponha que comecemos com um elétron em um determinado lugar e tempo (esse lugar e tempo recebendo o rótulo arbitrário A ) e um fóton em outro lugar e tempo (dado o rótulo B ). Uma pergunta típica do ponto de vista físico é: "Qual é a probabilidade de encontrar um elétron em C (outro lugar e um momento posterior) e um fóton em D (ainda outro lugar e tempo)?". O processo mais simples para atingir esse fim é o elétron se mover de A para C (uma ação elementar) e o fóton de B para D (outra ação elementar). A partir do conhecimento das amplitudes de probabilidade de cada um desses subprocessos - E ( A a C ) e P ( B a D ) - esperaríamos calcular a amplitude de probabilidade de ambos acontecerem juntos, multiplicando-os, usando a regra b) acima . Isso dá uma amplitude de probabilidade geral estimada simples, que é elevada ao quadrado para dar uma probabilidade estimada.

Efeito Compton

Mas existem outras maneiras pelas quais o resultado final pode ocorrer. O elétron pode se mover para um lugar e tempo E , onde absorve o fóton; em seguida, siga em frente antes de emitir outro fóton em F ; em seguida, passar para C , onde é detectado, enquanto os novos movimentos de fotões para D . A probabilidade desse processo complexo pode ser calculada novamente conhecendo as amplitudes de probabilidade de cada uma das ações individuais: três ações de elétrons, duas ações de fótons e dois vértices - uma emissão e uma absorção. Nós esperaria encontrar uma amplitude de probabilidade multiplicando as amplitudes de probabilidade de cada uma das acções, por quaisquer posições pretendidas para a E e F . Em seguida, usando a regra a) acima, tem que somar todas essas amplitudes de probabilidade para todas as alternativas para E e F . (Isso não é elementar na prática e envolve integração .) Mas há outra possibilidade, que é que o elétron primeiro se mova para G , onde emite um fóton, que segue para D , enquanto o elétron se move para H , onde absorve o primeiro fóton, antes de passar para C . Novamente, podemos calcular a amplitude de probabilidade dessas possibilidades (para todos os pontos G e H ). Temos, então, uma estimativa melhor para a amplitude de probabilidade total, adicionando as amplitudes de probabilidade dessas duas possibilidades à nossa estimativa simples original. A propósito, o nome dado a esse processo de um fóton interagindo com um elétron dessa forma é espalhamento Compton .

Há um número infinito de outros processos "virtuais" intermediários nos quais cada vez mais fótons são absorvidos e / ou emitidos. Para cada um desses processos, há um diagrama de Feynman que o descreve. Isso implica em um cálculo complexo para as amplitudes de probabilidade resultantes, mas desde que quanto mais complicado o diagrama, menos ele contribui para o resultado, é apenas uma questão de tempo e esforço encontrar uma resposta tão precisa quanto se deseja para a pergunta original. Esta é a abordagem básica do QED. Para calcular a probabilidade de qualquer processo interativo entre elétrons e fótons, é uma questão de primeiro observar, com os diagramas de Feynman, todas as maneiras possíveis pelas quais o processo pode ser construído a partir dos três elementos básicos. Cada diagrama envolve alguns cálculos envolvendo regras definidas para encontrar a amplitude de probabilidade associada.

Esse andaime básico permanece quando se passa para uma descrição quântica, mas algumas mudanças conceituais são necessárias. Uma é que, embora possamos esperar em nossa vida cotidiana que haja algumas restrições nos pontos para os quais uma partícula pode se mover, isso não é verdade na eletrodinâmica quântica completa. Há uma amplitude de probabilidade diferente de zero de um elétron em A , ou um fóton em B , movendo-se como uma ação básica para qualquer outro lugar e tempo no universo . Isso inclui lugares que só poderiam ser alcançados em velocidades maiores do que a da luz e também em tempos anteriores . (Um elétron se movendo para trás no tempo pode ser visto como um pósitron se movendo para frente no tempo.)

Amplitudes de probabilidade

Feynman substitui números complexos por setas giratórias, que começam na emissão e terminam na detecção de uma partícula. A soma de todas as setas resultantes dá uma seta final cujo comprimento ao quadrado é igual à probabilidade do evento. Neste diagrama, a luz emitida pela fonte S pode alcançar o detector em P refletindo no espelho (em azul) em vários pontos. Cada um dos caminhos tem uma seta associada a ele (cuja direção muda uniformemente com o tempo que a luz leva para percorrer o caminho). Para calcular corretamente a probabilidade total da luz atingir P começando em S , é necessário somar as setas para todos esses caminhos. O gráfico abaixo mostra o tempo total gasto para percorrer cada um dos caminhos acima.

A mecânica quântica introduz uma mudança importante na forma como as probabilidades são calculadas. As probabilidades ainda são representadas pelos números reais usuais que usamos para probabilidades em nosso mundo cotidiano, mas as probabilidades são calculadas como o módulo quadrado das amplitudes de probabilidade , que são números complexos .

Feynman evita expor o leitor à matemática dos números complexos usando uma representação simples, mas precisa deles como setas em um pedaço de papel ou tela. (Elas não devem ser confundidas com as setas dos diagramas de Feynman, que são representações simplificadas em duas dimensões de uma relação entre pontos em três dimensões do espaço e uma do tempo.) As setas de amplitude são fundamentais para a descrição do mundo dada pelo quantum teoria. Eles estão relacionados às nossas idéias cotidianas de probabilidade pela regra simples de que a probabilidade de um evento é o quadrado do comprimento da seta de amplitude correspondente. Assim, para um determinado processo, se duas amplitudes de probabilidade, v e w , estiverem envolvidas, a probabilidade do processo será dada por

${\displaystyle P=|\mathbf {v} +\mathbf {w} |^{2}}$

ou

${\displaystyle P=|\mathbf {v} \,\mathbf {w} |^{2}.}$

As regras em relação à adição ou multiplicação, entretanto, são as mesmas acima. Mas onde você esperaria adicionar ou multiplicar probabilidades, em vez disso, você adiciona ou multiplica amplitudes de probabilidade que agora são números complexos.

Adição de amplitudes de probabilidade como números complexos

Multiplicação de amplitudes de probabilidade como números complexos

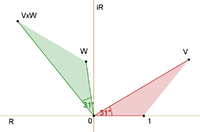
A adição e a multiplicação são operações comuns na teoria dos números complexos e são apresentadas nas figuras. A soma é encontrada da seguinte forma. Deixe o início da segunda seta estar no final da primeira. A soma é então uma terceira seta que vai diretamente do início da primeira ao final da segunda. O produto de duas setas é uma flecha cujo comprimento é o produto dos dois comprimentos. A direção do produto é encontrada somando os ângulos pelos quais cada um dos dois foi girado em relação a uma direção de referência: isso dá o ângulo em que o produto é girado em relação à direção de referência.

Essa mudança, de probabilidades para amplitudes de probabilidade, complica a matemática sem alterar a abordagem básica. Mas essa mudança ainda não é suficiente porque deixa de levar em conta o fato de que fótons e elétrons podem ser polarizados, o que significa que suas orientações no espaço e no tempo devem ser levadas em consideração. Portanto, P ( A a B ) consiste em 16 números complexos ou setas de amplitude de probabilidade. Existem também algumas pequenas alterações relacionadas à quantidade j , que pode ter que ser girada por um múltiplo de 90 ° para algumas polarizações, o que é de interesse apenas para a contabilidade detalhada.

Associado ao fato de que o elétron pode ser polarizado está outro pequeno detalhe necessário, que está conectado ao fato de que um elétron é um férmion e obedece às estatísticas de Fermi-Dirac . A regra básica é que se temos a amplitude de probabilidade para um dado processo complexo envolvendo mais de um elétron, então quando incluímos (como sempre devemos) o diagrama de Feynman complementar no qual trocamos dois eventos de elétrons, a amplitude resultante é o inverso - o negativo - do primeiro. O caso mais simples seria dois electrões a partir de A e B terminando em C e D . A amplitude seria calculada como a "diferença", E ( A para D ) × E ( B para C ) - E ( A para C ) × E ( B para D ) , onde esperaríamos, de nossa ideia cotidiana de probabilidades , que seria uma soma.

Propagadores

Finalmente, deve-se calcular P ( A a B ) e E ( C a D ) correspondendo às amplitudes de probabilidade para o fóton e o elétron, respectivamente. Estas são essencialmente as soluções da equação de Dirac , que descreve o comportamento da amplitude de probabilidade do elétron e as equações de Maxwell , que descrevem o comportamento da amplitude de probabilidade do fóton. Eles são chamados de propagadores de Feynman . A tradução para uma notação comumente usada na literatura padrão é a seguinte:

${\displaystyle P(A{\text{ to }}B)\to D_{F}(x_{B}-x_{A}),\quad E(C{\text{ to }}D)\to S_{F}(x_{D}-x_{C}),}$

em que um símbolo de forma abreviada, tais como suportes para os quatro números reais que dão o tempo e a posição em três dimensões do ponto marcado Uma . ${\displaystyle x_{A}}$

Renormalização em massa

Loop de autoenergia de elétrons

Surgiu um problema historicamente que impediu o progresso por vinte anos: embora comecemos com a suposição de três ações "simples" básicas, as regras do jogo dizem que se quisermos calcular a amplitude de probabilidade de um elétron ir de A a B , devemos levar em consideração todas as maneiras possíveis: todos os diagramas de Feynman possíveis com esses terminais. Assim, haverá uma maneira em que o electrão desloca para C , emite um fotão lá e em seguida absorve-lo novamente no D antes de passar para B . Ou pode fazer esse tipo de coisa duas vezes, ou mais. Em suma, temos uma situação semelhante a um fractal em que se olharmos de perto para uma linha, ela se divide em uma coleção de linhas "simples", cada uma das quais, se examinada de perto, é por sua vez composta de linhas "simples" e assim por diante ad infinitum . Esta é uma situação desafiadora de lidar. Se adicionar esse detalhe apenas alterasse as coisas ligeiramente, então não teria sido tão ruim, mas o desastre aconteceu quando foi descoberto que a correção simples mencionada acima levava a amplitudes de probabilidade infinitas . Com o tempo, esse problema foi "consertado" pela técnica de renormalização . No entanto, o próprio Feynman permaneceu insatisfeito com isso, chamando-o de "processo dippy".

Conclusões

Dentro da estrutura acima, os físicos foram então capazes de calcular com um alto grau de precisão algumas das propriedades dos elétrons, como o momento de dipolo magnético anômalo . No entanto, como Feynman aponta, não consegue explicar por que partículas como o elétron têm as massas que têm. "Não existe uma teoria que explique adequadamente esses números. Usamos os números em todas as nossas teorias, mas não os entendemos - o que são ou de onde vêm. Acredito que, de um ponto de vista fundamental, isso é um problema muito interessante e sério. "

Formulação matemática

Matematicamente, QED é uma teoria de calibre abeliana com o grupo de simetria U (1) . O campo de medição , que medeia a interação entre os campos carregados de spin-1/2 , é o campo eletromagnético . O QED Lagrangiano para um campo de spin-1/2 interagindo com o campo eletromagnético é dado em unidades naturais pela parte real de

Onde

${\displaystyle \gamma ^{\mu }}$são matrizes de Dirac ;

${\displaystyle \psi }$um campo bispinor de partículas de spin 1/2 (por exemplo, campo elétron - pósitron );

${\displaystyle {\bar {\psi }}\equiv \psi ^{\dagger }\gamma ^{0}}$, chamado "psi-bar", às vezes é referido como o adjunto de Dirac ;

${\displaystyle D_{\mu }\equiv \partial _{\mu }+ieA_{\mu }+ieB_{\mu }\,\!}$é a derivada covariante de calibre ;

e é a constante de acoplamento , igual à carga elétrica do campo bispinor;

m é a massa do elétron ou pósitron;

${\displaystyle A_{\mu }}$é o quatro potencial covariante do campo eletromagnético gerado pelo próprio elétron;

${\displaystyle B_{\mu }}$ é o campo externo imposto por fonte externa;

${\displaystyle F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\,\!}$é o tensor de campo eletromagnético .

Equações de movimento

Substituir a definição de D no Lagrangiano dá

${\displaystyle {\mathcal {L}}=i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi -e{\bar {\psi }}\gamma ^{\mu }(A_{\mu }+B_{\mu })\psi -m{\bar {\psi }}\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }.}$

A partir desse Lagrangiano, as equações de movimento para os campos ψ e A podem ser obtidas.

• Usando a equação de Euler-Lagrange da teoria de campo para ψ ,

${\displaystyle \partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\psi )}}\right)-{\frac {\partial {\mathcal {L}}}{\partial \psi }}=0.}$

( 2 )

As derivadas do Lagrangiano em relação a ψ são

${\displaystyle \partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\psi )}}\right)=\partial _{\mu }\left(i{\bar {\psi }}\gamma ^{\mu }\right),}$

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial \psi }}=-e{\bar {\psi }}\gamma ^{\mu }(A_{\mu }+B_{\mu })-m{\bar {\psi }}.}$

Inserir estes em ( 2 ) resulta em

${\displaystyle i\partial _{\mu }{\bar {\psi }}\gamma ^{\mu }+e{\bar {\psi }}\gamma ^{\mu }(A_{\mu }+B_{\mu })+m{\bar {\psi }}=0,}$

com conjugado hermitiano

${\displaystyle i\gamma ^{\mu }\partial _{\mu }\psi -e\gamma ^{\mu }(A_{\mu }+B_{\mu })\psi -m\psi =0.}$

Trazer o termo do meio para o lado direito produz

O lado esquerdo é como a equação de Dirac original e o lado direito é a interação com o campo eletromagnético.

• Usando a equação de Euler-Lagrange para o campo A ,

${\displaystyle \partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)-{\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=0,}$

( 3 )

os derivados desta vez são

${\displaystyle \partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)=\partial _{\nu }\left(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }\right),}$

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=-e{\bar {\psi }}\gamma ^{\mu }\psi .}$

Substituindo de volta em ( 3 ) leva a

Agora, se impormos a condição de medidor de Lorenz

${\displaystyle \partial _{\mu }A^{\mu }=0,}$

as equações reduzem a

${\displaystyle \Box A^{\mu }=e{\bar {\psi }}\gamma ^{\mu }\psi ,}$

que é uma equação de onda para os quatro potenciais, a versão QED das equações clássicas de Maxwell no calibre de Lorenz . (O quadrado representa o operador de D'Alembert , .) ${\displaystyle \Box =\partial _{\alpha }\partial ^{\alpha }}$

Imagem de interação

Esta teoria pode ser quantizada diretamente tratando os setores bosônicos e fermiônicos como livres. Isso nos permite construir um conjunto de estados assintóticos que podem ser usados ​​para iniciar o cálculo das amplitudes de probabilidade para diferentes processos. Para isso, temos que calcular um operador de evolução , que para um dado estado inicial dará um estado final de forma a ter ${\displaystyle |i\rangle }$${\displaystyle \langle f|}$

${\displaystyle M_{fi}=\langle f|U|i\rangle .}$

Essa técnica também é conhecida como S-matrix . O operador de evolução é obtido na imagem de interação , onde a evolução no tempo é dada pela Hamiltoniana de interação, que é a integral no espaço do segundo termo na densidade Lagrangiana dada acima:

${\displaystyle V=e\int d^{3}x\,{\bar {\psi }}\gamma ^{\mu }\psi A_{\mu },}$

e então, um tem

${\displaystyle U=T\exp \left[-{\frac {i}{\hbar }}\int _{t_{0}}^{t}dt'\,V(t')\right],}$

onde T é o operador de ordenação do tempo . Este operador de evolução só tem significado como uma série, e o que obtemos aqui é uma série de perturbações com a constante de estrutura fina como parâmetro de desenvolvimento. Esta série é chamada de série Dyson .

Diagramas de Feynman

Apesar da clareza conceitual dessa abordagem de Feynman para QED, quase nenhum livro texto o segue em sua apresentação. Ao realizar cálculos, é muito mais fácil trabalhar com as transformadas de Fourier dos propagadores . Os testes experimentais de eletrodinâmica quântica são normalmente experimentos de espalhamento. Na teoria de espalhamento, os momentos das partículas, em vez de suas posições, são considerados, e é conveniente pensar nas partículas como sendo criadas ou aniquiladas quando interagem. Os diagramas de Feynman têm a mesma aparência , mas as linhas têm interpretações diferentes. A linha do elétron representa um elétron com uma dada energia e momento, com uma interpretação semelhante da linha do fóton. Um diagrama de vértices representa a aniquilação de um elétron e a criação de outro junto com a absorção ou criação de um fóton, cada um tendo energias e momentos específicos.

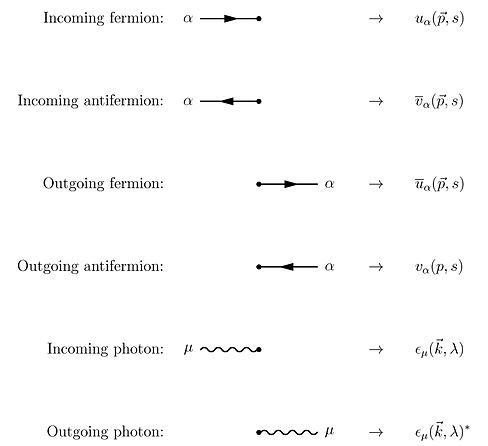
Usando o teorema de Wick nos termos da série de Dyson, todos os termos da matriz S para a eletrodinâmica quântica podem ser calculados através da técnica dos diagramas de Feynman . Neste caso, as regras para o sorteio são as seguintes

A essas regras, devemos adicionar mais uma para loops fechados que implica uma integração em momentos , uma vez que essas partículas internas ("virtuais") não são restritas a qualquer energia-momento específico, mesmo aquele normalmente exigido pela relatividade especial (ver Propagador para detalhes ) ${\displaystyle \int d^{4}p/(2\pi )^{4}}$

A partir deles, cálculos de amplitudes de probabilidade são dados diretamente. Um exemplo é o espalhamento Compton , com um elétron e um fóton passando por espalhamento elástico . Os diagramas de Feynman são, neste caso,

e assim somos capazes de obter a amplitude correspondente na primeira ordem de uma série de perturbações para a matriz S :

${\displaystyle M_{fi}=(ie)^{2}{\overline {u}}({\vec {p}}',s')\epsilon \!\!\!/\,'({\vec {k}}',\lambda ')^{*}{\frac {p\!\!\!/+k\!\!\!/+m_{e}}{(p+k)^{2}-m_{e}^{2}}}\epsilon \!\!\!/({\vec {k}},\lambda )u({\vec {p}},s)+(ie)^{2}{\overline {u}}({\vec {p}}',s')\epsilon \!\!\!/({\vec {k}},\lambda ){\frac {p\!\!\!/-k\!\!\!/'+m_{e}}{(p-k')^{2}-m_{e}^{2}}}\epsilon \!\!\!/\,'({\vec {k}}',\lambda ')^{*}u({\vec {p}},s),}$

a partir do qual podemos calcular a seção transversal para este espalhamento.

Fenômenos não perturbativos

O sucesso preditivo da eletrodinâmica quântica repousa em grande parte no uso da teoria de perturbação, expressa em diagramas de Feynman. No entanto, a eletrodinâmica quântica também leva a previsões além da teoria de perturbação. Na presença de campos elétricos muito fortes, ele prediz que elétrons e pósitrons serão produzidos espontaneamente, causando a decadência do campo. Esse processo, chamado de efeito Schwinger , não pode ser entendido em termos de nenhum número finito de diagramas de Feynman e, portanto, é descrito como não perturbativo . Matematicamente, pode ser derivado por uma aproximação semiclássica da integral de caminho da eletrodinâmica quântica.

Renormalizabilidade

Os termos de ordem superior podem ser calculados diretamente para o operador de evolução, mas esses termos exibem diagramas contendo os seguintes mais simples

• 

  Contribuição de um circuito para a função de polarização a vácuo${\displaystyle \Pi }$

• 

  Contribuição de um loop para o elétron auto-energia função${\displaystyle \Sigma }$

• 

  Contribuição de um laço para a função de vértice ${\displaystyle \Gamma }$

que, sendo loops fechados, implicam na presença de integrais divergentes sem significado matemático. Para superar essa dificuldade, uma técnica chamada renormalização foi desenvolvida, produzindo resultados finitos em concordância muito próxima com os experimentos. Um critério para a teoria ser significativa após a renormalização é que o número de diagramas divergentes é finito. Neste caso, a teoria é dita "renormalizável". A razão para isso é que, para renormalizar os observáveis, é necessário um número finito de constantes para manter o valor preditivo da teoria intocado. Este é exatamente o caso da eletrodinâmica quântica que exibe apenas três diagramas divergentes. Este procedimento fornece observáveis ​​em concordância muito próxima com o experimento, como visto, por exemplo, para a razão giromagnética do elétron .

A renormalizabilidade tornou-se um critério essencial para que uma teoria quântica de campos seja considerada viável. Todas as teorias que descrevem interações fundamentais , exceto gravitação , cuja contraparte quântica é apenas conjectural e atualmente sob pesquisa muito ativa, são teorias renormalizáveis.

Não convergência de série

Um argumento de Freeman Dyson mostra que o raio de convergência da série de perturbações em QED é zero. O argumento básico é o seguinte: se a constante de acoplamento fosse negativa, isso seria equivalente à constante de força de Coulomb ser negativa. Isso iria "reverter" a interação eletromagnética de modo que cargas semelhantes se atraíssem e cargas diferentes se repelissem . Isso tornaria o vácuo instável contra a decadência em um aglomerado de elétrons de um lado do universo e um aglomerado de pósitrons do outro lado do universo. Como a teoria está "doente" para qualquer valor negativo da constante de acoplamento, as séries não convergem, mas são, na melhor das hipóteses, uma série assintótica .

De uma perspectiva moderna, dizemos que QED não é bem definido como uma teoria quântica de campos para energia arbitrariamente alta. A constante de acoplamento vai até o infinito em energia finita, sinalizando um pólo de Landau . O problema é essencialmente que o QED parece sofrer de problemas de trivialidade quântica . Esta é uma das motivações para incorporar o QED em uma Grande Teoria Unificada .

Veja também

Referências

Leitura adicional

Livros

• De Broglie, Louis (1925). Recherches sur la theory des quanta [Pesquisa em teoria quântica] . França: Wiley-Interscience.
• Feynman, Richard Phillips (1998). Quantum Electrodynamics (New ed.). Westview Press. ISBN 978-0-201-36075-2.
• Jauch, JM; Rohrlich, F. (1980). A Teoria dos Fótons e Elétrons . Springer-Verlag. ISBN 978-0-387-07295-1.
• Greiner, Walter; Bromley, DA; Müller, Berndt (2000). Teoria de Gauge das Interações Fracas . Springer. ISBN 978-3-540-67672-0.
• Kane, Gordon, L. (1993). Física Moderna de Partículas Elementares . Westview Press. ISBN 978-0-201-62460-1.
• Miller, Arthur I. (1995). Early Quantum Electrodynamics: A Sourcebook . Cambridge University Press. ISBN 978-0-521-56891-3.
• Milonni, Peter W. (1994). The Quantum Vacuum: An Introduction to Quantum Electrodynamics . Boston: Academic Press. ISBN 0124980805. LCCN  93029780 . OCLC  422797902 .
• Schweber, Silvan S. (1994). QED e os homens que o fizeram . Princeton University Press. ISBN 978-0-691-03327-3.
• Schwinger, Julian (1958). Artigos Selecionados em Eletrodinâmica Quântica . Publicações de Dover. ISBN 978-0-486-60444-2.
• Tannoudji-Cohen, Claude ; Dupont-Roc, Jacques; Grynberg, Gilbert (1997). Fótons e átomos: Introdução à Eletrodinâmica Quântica . Wiley-Interscience. ISBN 978-0-471-18433-1.

Diários

• Dudley, JM; Kwan, AM (1996). "Palestras populares de Richard Feynman sobre eletrodinâmica quântica: as palestras Robb de 1979 na Universidade de Auckland". American Journal of Physics . 64 (6): 694–98. Bibcode : 1996AmJPh..64..694D . doi : 10.1119 / 1.18234 .

links externos

• Palestra do Prêmio Nobel de Feynman descrevendo a evolução do QED e seu papel nele
• Palestras de Feynman na Nova Zelândia sobre QED para não físicos
• http://qed.wikina.org/ - Animações demonstrando QED