Matemática do Sudoku - Mathematics of Sudoku

Um Sudoku automórfico de 24 pistas com simetria translacional

Os quebra- cabeças do Sudoku podem ser estudados matematicamente para responder a perguntas como "Quantas grades de Sudoku preenchidas existem?" , " Qual é o número mínimo de pistas em um quebra-cabeça válido? " E "De que maneiras as grades do Sudoku podem ser simétricas?" através do uso de combinatória e teoria dos grupos .

Os principais resultados são que para o Sudoku clássico o número de grades preenchidas é 6.670.903.752.021.072.936.960 (6,67 × 10 ²¹ ), o que reduz a 5.472.730.538 grupos essencialmente diferentes sob as transformações de preservação de validade . Existem 26 tipos de simetria, mas eles só podem ser encontrados em cerca de 0,005% de todas as grades preenchidas. Um quebra-cabeça com uma solução única deve ter pelo menos 17 pistas, e há um quebra-cabeça solucionável com no máximo 21 pistas para cada grade resolvida. O maior quebra-cabeça mínimo encontrado até agora tem 40 pistas.

Resultados semelhantes são conhecidos para variantes e grades menores. Não são conhecidos resultados exatos para Sudokus maiores do que a grade clássica 9 × 9, embora haja estimativas que se acredita serem bastante precisas.

Visão geral

A análise do Sudoku se divide em duas áreas principais:

analisando as propriedades de grades concluídas
analisar as propriedades de quebra-cabeças concluídos.

A análise inicial foi amplamente focada na enumeração de soluções, com resultados aparecendo pela primeira vez em 2004.

Existem muitas variantes do Sudoku , parcialmente caracterizadas pelo tamanho ( N ) e pela forma de suas regiões . A menos que indicado, a discussão neste artigo assume o Sudoku clássico, ou seja, N = 9 (uma grade 9 × 9 e regiões 3 × 3). Um Sudoku rectangular utiliza regiões rectangulares de linha-coluna dimensão R × C . Outras variantes incluem aquelas com regiões de formato irregular ou com restrições adicionais ( hipercubo ) ou diferentes tipos de restrições ( Samunamupure ).

As regiões também são chamadas de blocos ou caixas . Uma banda é uma parte da grade que encapsula 3 linhas e 3 caixas, e uma pilha é uma parte da grade que encapsula 3 colunas e 3 caixas. Um quebra - cabeça é uma grade parcialmente preenchida e os valores iniciais são dados ou pistas . Um quebra-cabeça adequado tem uma solução única. Um quebra-cabeça mínimo é um quebra-cabeça adequado do qual nenhuma pista pode ser removida sem a introdução de soluções adicionais. Consulte o Glossário de Sudoku para outras terminologias.

Resolver Sudokus do ponto de vista de um jogador foi explorado no livro de Denis Berthier "The Hidden Logic of Sudoku" (2007), que considera estratégias como "cadeias xy ocultas".

Contexto matemático

O problema geral de resolver quebra-cabeças de Sudoku em n ² × n ² grades de n × n blocos é conhecido como NP-completo . Para n = 3 (Sudoku clássico), entretanto, esse resultado é de pouca relevância prática: algoritmos podem resolver quebra-cabeças em uma fração de segundo devido ao pequeno tamanho do problema.

Um quebra-cabeça pode ser expresso como um problema de coloração de gráfico . O objetivo é construir uma coloração 9 de um gráfico particular, dada uma coloração 9 parcial. O gráfico Sudoku possui 81 vértices, um vértice para cada célula. Os vértices são rotulados com pares ordenados ( x , y ), onde x e y são inteiros entre 1 e 9. Neste caso, dois vértices distintos rotulados por ( x , y ) e ( x ′, y ′) são unidos por um borda se e somente se :

x = x ′ (mesma coluna) ou,
y = y ′ (mesma linha) ou,
⌈ x / 3 ⌉ = ⌈ x ′ / 3 ⌉ e ⌈ y / 3 ⌉ = ⌈ y ′ / 3 ⌉ (mesma célula 3 × 3)

O quebra-cabeça é então completado atribuindo-se um inteiro entre 1 e 9 a cada vértice, de forma que os vértices unidos por uma aresta não tenham o mesmo inteiro atribuído a eles.

Uma grade de solução Sudoku também é um quadrado latino . Existem significativamente menos grades de Sudoku do que quadrados latinos porque o Sudoku impõe a restrição regional adicional.

Sudokus das mesas de grupo

Como no caso dos quadrados latinos, as tabelas de (adição ou) multiplicação ( tabelas de Cayley ) de grupos finitos podem ser usadas para construir Sudokus e tabelas de números relacionadas. Ou seja, deve-se levar em consideração os subgrupos e grupos de quociente :

Tomemos por exemplo o grupo de pares, adicionando cada componente separadamente modulo alguns . Ao omitir um dos componentes, de repente nos encontramos (e este mapeamento é obviamente compatível com os respectivos acréscimos, ou seja, é um homomorfismo de grupo ). Também se diz que o último é um grupo quociente do primeiro, porque alguns elementos, uma vez diferentes, tornam-se iguais no novo grupo. No entanto, também é um subgrupo, porque podemos simplesmente preencher o componente que falta com para voltar . ${\ displaystyle \ mathbb {Z} _ {n} \ oplus \ mathbb {Z} _ {n}}$ ${\ displaystyle n}$ ${\ displaystyle \ mathbb {Z} _ {n}}$ ${\ displaystyle 0}$ ${\ displaystyle \ mathbb {Z} _ {n} \ oplus \ mathbb {Z} _ {n}}$

Sob essa visão, escrevemos o exemplo, Grade 1 , para . ${\ displaystyle n = 3}$

Cada região do Sudoku tem a mesma aparência no segundo componente (ou seja, como o subgrupo ), porque eles são adicionados independentemente do primeiro. Por outro lado, os primeiros componentes são iguais em cada bloco, e se imaginarmos cada bloco como uma célula, esses primeiros componentes mostram o mesmo padrão (ou seja, o grupo de quocientes ). Conforme descrito no artigo dos quadrados latinos, este é um quadrado latino de ordem . ${\ displaystyle \ mathbb {Z} _ {3}}$ ${\ displaystyle \ mathbb {Z} _ {3}}$ ${\ displaystyle 9}$

Agora, para produzir um Sudoku, vamos permutar as linhas (ou equivalentemente as colunas) de forma que cada bloco seja redistribuído exatamente uma vez em cada bloco - por exemplo, ordene-os . Isso, é claro, preserva a propriedade da Praça Latina. Além disso, em cada bloco as linhas têm um primeiro componente distinto por construção e cada linha em um bloco tem entradas distintas por meio do segundo componente, porque os segundos componentes dos blocos formaram originalmente um quadrado latino de ordem (do subgrupo ). Assim, chegamos a um Sudoku (renomeie os pares para os números 1 ... 9 se desejar). Com o exemplo e a permutação de linha acima, chegamos à Grade 2 . ${\ displaystyle 1,4,7,2,5,8,3,6,9}$ ${\ displaystyle 3}$ ${\ displaystyle \ mathbb {Z} _ {3}}$

Grade 1 - A tabela de adição em

{\ displaystyle \ mathbb {Z} _ {3} \ oplus \ mathbb {Z} _ {3}}

(0,0)	(0,1)	(0,2)
(0,1)	(0,2)	(0,0)
(0,2)	(0,0)	(0,1)

(1,0)	(1,1)	(1,2)
(1,1)	(1,2)	(1,0)
(1,2)	(1,0)	(1,1)

(2,0)	(2,1)	(2,2)
(2,1)	(2,2)	(2,0)
(2,2)	(2,0)	(2,1)

(1,0)	(1,1)	(1,2)
(1,1)	(1,2)	(1,0)
(1,2)	(1,0)	(1,1)

(2,0)	(2,1)	(2,2)
(2,1)	(2,2)	(2,0)
(2,2)	(2,0)	(2,1)

(0,0)	(0,1)	(0,2)
(0,1)	(0,2)	(0,0)
(0,2)	(0,0)	(0,1)

(2,0)	(2,1)	(2,2)
(2,1)	(2,2)	(2,0)
(2,2)	(2,0)	(2,1)

(0,0)	(0,1)	(0,2)
(0,1)	(0,2)	(0,0)
(0,2)	(0,0)	(0,1)

(1,0)	(1,1)	(1,2)
(1,1)	(1,2)	(1,0)
(1,2)	(1,0)	(1,1)

Grade 2 - Gerando um Sudoku

(0,0)	(0,1)	(0,2)
(1,0)	(1,1)	(1,2)
(2,0)	(2,1)	(2,2)

(1,0)	(1,1)	(1,2)
(2,0)	(2,1)	(2,2)
(0,0)	(0,1)	(0,2)

(2,0)	(2,1)	(2,2)
(0,0)	(0,1)	(0,2)
(1,0)	(1,1)	(1,2)

(0,1)	(0,2)	(0,0)
(1,1)	(1,2)	(1,0)
(2,1)	(2,2)	(2,0)

(1,1)	(1,2)	(1,0)
(2,1)	(2,2)	(2,0)
(0,1)	(0,2)	(0,0)

(2,1)	(2,2)	(2,0)
(0,1)	(0,2)	(0,0)
(1,1)	(1,2)	(1,0)

(0,2)	(0,0)	(0,1)
(1,2)	(1,0)	(1,1)
(2,2)	(2,0)	(2,1)

(1,2)	(1,0)	(1,1)
(2,2)	(2,0)	(2,1)
(0,2)	(0,0)	(0,1)

(2,2)	(2,0)	(2,1)
(0,2)	(0,0)	(0,1)
(1,2)	(1,0)	(1,1)

Para que esse método funcione, geralmente não é necessário um produto de dois grupos de tamanhos iguais. A chamada sequência exata curta de grupos finitos de tamanho apropriado já dá conta do recado. Tente, por exemplo, o grupo com quociente e subgrupo . Parece claro (já pelos argumentos de enumeração) que nem todos os Sudokus podem ser gerados dessa maneira. ${\ displaystyle \ mathbb {Z} _ {4}}$ ${\ displaystyle \ mathbb {Z} _ {2}}$

Variantes

Um Sudoku pode ser interpretado como um mosaico (ou cobertura ) de um quadrado latino com poliominós (as regiões do Sudoku). O clássico Sudoku 9 × 9 é feito de nonominós quadrados . É possível aplicar as regras do Sudoku a quebra-cabeças de outros tamanhos, embora apenas os quebra-cabeças N ² × N ² Sudoku possam ser ladrilhados com poliominós quadrados.

Consulte o Glossário de Sudoku para uma lista expandida de variantes.

Regiões retangulares

Uma variante popular é feita de regiões retangulares ( blocos ou caixas ) - por exemplo, hexominós 2 × 3 lado a lado em uma grade 6 × 6. A seguinte notação é usada para discutir esta variante:

R × C denota uma região retangular com R linhas e C colunas.
A configuração de grade implícita tem:
- dimensões da grade N × N , onde N = R × C
- N blocos ( caixas ) de tamanho R × C , dispostos em uma 'supergrid' C × R
- Bandas C de tamanho R × N , consistindo em blocos R horizontalmente adjacentes
- Pilhas R de tamanho N × C , consistindo em blocos C verticalmente adjacentes

Sudoku com regiões N × N quadradas são mais simétricos do que Sudoku retangular, uma vez que cada linha e coluna intercepta N regiões e compartilha N células com cada uma. O número de bandas e pilhas também é igual a N . O Sudoku "3 × 3" é adicionalmente único: N é também o número de restrições linha-coluna-região da Regra Única (ou seja, há N = 3 tipos de unidades ).

Sudokus Jigsaw

Um Sudoku cujas regiões não são (necessariamente) quadradas ou retangulares é conhecido como Jigsaw Sudoku. Em particular, uma N × N praça onde N é primo só pode estar lado a lado com irregulares N -ominoes . Para pequenos valores de N, o número de maneiras de agrupar o quadrado (excluindo simetrias) foi calculado (sequência A172477 no OEIS ). Para N ≥ 4, algumas dessas telhas não são compatíveis com nenhum quadrado latino; ou seja, todos os quebra-cabeças de Sudoku em tal ladrilho não têm solução.

Soluções

A resposta à pergunta 'Quantas grades de Sudoku existem?' depende da definição de quando soluções semelhantes são consideradas diferentes.

Sudoku comum

Todas as soluções

Para a enumeração de todas as soluções possíveis, duas soluções são consideradas distintas se algum de seus valores de célula (81) correspondentes diferir. As relações de simetria entre soluções semelhantes são ignoradas, por exemplo, as rotações de uma solução são consideradas distintas. As simetrias desempenham um papel significativo na estratégia de enumeração, mas não na contagem de todas as soluções possíveis.

A primeira solução conhecida para completar a enumeração foi postada por QSCGZ (Guenter Stertenbrink) no grupo de notícias rec.puzzles em 2003, obtendo 6.670.903.752.021.072.936.960 (6,67 × 10 ²¹ ) soluções distintas.

Em um estudo de 2005, Felgenhauer e Jarvis analisaram as permutações da banda superior usada em soluções válidas. Uma vez que as simetrias Band1 e classes de equivalência para as soluções de grade parcial foram identificadas, as conclusões das duas bandas inferiores foram construídas e contadas para cada classe de equivalência. A soma das conclusões sobre as classes de equivalência, ponderadas pelo tamanho da classe, dá o número total de soluções como 6.670.903.752.021.072.936.960, confirmando o valor obtido por QSCGZ. O valor foi posteriormente confirmado inúmeras vezes de forma independente. Uma segunda técnica de enumeração baseada na geração de banda foi desenvolvida posteriormente e é significativamente menos intensiva em termos de computação. Essa técnica subsequente resultou na necessidade de aproximadamente 1/97 do número de ciclos de computação das técnicas originais, mas era significativamente mais complicada de configurar.

Soluções essencialmente diferentes

Transformações de preservação de validade

Duas grades válidas são essencialmente as mesmas se uma puder ser derivada da outra, usando a chamada transformação de preservação de validade (VPT) . Essas transformações sempre transformam uma grade válida em outra grade válida. Existem dois tipos principais: permutações de símbolos (reclassificação) e permutações de células (rearranjos). Eles são:

Símbolos de reetiquetagem (9!)
(Uma vez que todas as combinações de reetiquetagem possíveis são eliminadas, exceto uma: por exemplo, mantendo a linha superior fixa em [123456789], o número de grades fixas reduz para 18.383.222.420.692.992. Este valor é 6.670.903.752.021.072.936.960 dividido por 9!)

e reorganizando (embaralhamento):

Permutações de banda (3!)
Permutações de linha dentro de uma banda (3! × 3! × 3!)
Permutações de pilha (3!)
Permutações de coluna dentro de uma pilha (3! × 3! × 3!)
Reflexão, transposição e rotação (2)
(Dada uma única transposição ou rotação de quarto de volta em conjunto com as permutações acima, qualquer combinação de reflexões, transposições e rotações pode ser produzida, portanto, essas operações contribuem apenas com um fator de 2)

Essas operações definem uma relação entre grades equivalentes. Com respeito aos 81 valores das células da grade, as operações de reorganização formam um subgrupo do grupo simétrico S ₈₁ , de ordem 3! ⁸ × 2 = 3.359.232. As operações de reclassificação são isomórficas com S ₉ e geram um 9 adicional! = 362.880 grades equivalentes. Aplicar essas operações em uma grade resulta em 3! ⁸ × 2 × 9! ou 1.218.998.108.160 grades essencialmente equivalentes. No entanto, há um pequeno número de sudokus para os quais as operações acima geram menos grades; estes são os sudokus auto-semelhantes ou automórficos . Apenas cerca de 0,01% de todas as grades essencialmente únicas são automórficas, mas contá-las é necessário para avaliar o número exato de sudokus essencialmente diferentes.

O grupo de simetria sudoku

A estrutura precisa do grupo de simetria do sudoku pode ser expressa sucintamente usando o produto coroa (≀). As possíveis permutações de linha (ou coluna) formam um grupo isomórfico a S ₃ ≀ S ₃ de ordem 3! ⁴ = 1.296. Todo o grupo de rearranjo é formado deixando a operação de transposição (isomórfica para C ₂ ) atuar em duas cópias desse grupo, uma para as permutações de linha e outra para as permutações de coluna. Este é S ₃ ≀ S ₃ ≀ C ₂ , um grupo da ordem 1.296 ² × 2 = 3.359.232. Finalmente, as operações de reclassificação comutam com as operações de rearranjo, então o grupo sudoku completo (VPT) é ( S ₃ ≀ S ₃ ≀ C ₂ ) × S ₉ da ordem 1.218.998.108.160.

Pontos fixos e lema de Burnside

O conjunto de grades equivalentes que podem ser alcançadas usando essas operações (excluindo a reclassificação) forma uma órbita de grades sob a ação do grupo de rearranjo . O número de soluções essencialmente diferentes é então o número de órbitas, que pode ser calculado usando o lema de Burnside . Os pontos fixos de Burnside são grades que não mudam durante a operação de rearranjo ou apenas diferem pela reclassificação. Para simplificar o cálculo, os elementos do grupo de rearranjo são classificados em classes de conjugação , cujos elementos têm todos o mesmo número de pontos fixos. Acontece que apenas 27 das 275 classes de conjugação do grupo de rearranjo têm pontos fixos; essas classes de conjugação representam os diferentes tipos de simetria (auto-similaridade ou automorfismo) que podem ser encontrados em grades de sudoku completas. Usando essa técnica, Ed Russell e Frazer Jarvis foram os primeiros a calcular o número de soluções de sudoku essencialmente diferentes como 5.472.730.538 .

Classes de conjugação do grupo de rearranjo com pontos fixos ("automorfismos" e sua prevalência)
Nome ou composição	Código	Id da classe .	Tamanho da classe	Ciclos celulares	O	F	Número de grades fixas (até a reclassificação), por elemento	Número de grades fixas, por elemento	Número de grades fixas (até a reclassificação), toda a classe	Número de grades fixas, toda a classe
Identidade	e	1	1		1	81	18.383.222.420.692.992	6.670.903.752.021.072.936.960	18.383.222.420.692.992	6.670.903.752.021.072.936.960
Mini Fileiras (MR)	ccc	8	16	27 × 3	3	0	107.495.424	39.007.939.461.120	1.719.926.784	624.127.031.377.920
2 MR, 1 MD	ccc \| c	7	96	27 × 3	3	0	21.233.664	7.705.271.992.320	2.038.431.744	739.706.111.262.720
1 MR, 2 MD	ccc \| cc	9	192	27 × 3	3	0	4.204.224	1.525.628.805.120	807.211.008	292.920.730.583.040
Mini diagonais (MD)	ccc \| ccc	10	64	27 × 3	3	0	2.508.084	910.133.521.920	160.517.376	58.248.545.402.880
Saltar linhas (JR)	C	25	144	27 × 3	3	0	14.837.760	5.384.326.348.800	2.136.637.440	775.342.994.227.200
2 JR, 1 GR	C \| c	28	864	27 × 3	3	0	2.085.120	756.648.345.600	1.801.543.680	653.744.170.598.400
1 JR, 2 GR	C \| cc	30	1.728	27 × 3	3	0	294.912	107.017.666.560	509.607.936	184.926.527.815.680
Linhas planas (GR)	C \| ccc	32	1.152	27 × 3	3	0	6.342.480	2.301.559.142.400	7.306.536.960	2.651.396.132.044.800
Linhas completas (FR)	C9	27	288	9 × 9	9	0	5.184	1.881.169.920	1.492.992	541.776.936.960
2 FR, 1 WR	C9 \| c	26	1.728	9 × 9	9	0	2.592	940.584.960	4.478.976	1.625.330.810.880
1 FR, 2 WR	C9 \| cc	29	3.456	9 × 9	9	0	1.296	470.292.480	4.478.976	1.625.330.810.880
Linhas ondulantes (WR)	C9 \| ccc	31	2.304	9 × 9	9	0	648	235.146.240	1.492.992	541.776.936.960
Diagonais de salto (JD)	C \| C	22	5.184	27 × 3	3	0	323.928	117.546.992.640	1.679.242.752	609.363.609.845.760
Colunas Quebradas (BC)	C \| C9	24	20.736	9 × 9	9	0	288	104.509.440	5.971.968	2.167.107.747.840
Diagonais Completas (FD)	C9 \| C9	23	20.736	9 × 9	9	0	162	58.786.560	3.359.232	1.218.998.108.160
Espelho Diagonal (DM)	T	37	1.296	36 × 2	2	9	30.258.432	10.980.179.804.160	39.214.927.872	14.230.313.026.191.360
DM + MD	T ccc	40	10.368	3 × 3, 12 × 6	6	0	1.854	672.779.520	19.222.272	6.975.378.063.360
DM + JD	TC	43	93.312	3 × 3, 12 × 6	6	0	288	104.509.440	26.873.856	9.751.984.865.280
Quarto de volta (QT)	T sS	86	69.984	20 × 4	4	1	13.056	4.737.761.280	913.711.104	331.567.485.419.520
Meia volta (HT)	sS \| WL	79	2.916	40 × 2	2	1	155.492.352	56.425.064.693.760	453.415.698.432	164.535.488.647.004.160
Varetas de coluna (CS)	S \| sss	134	972	36 × 2	2	9	449.445.888	163.094.923.837.440	436.861.403.136	158.528.265.969.991.680
CS + MC	cS6 \| sss	135	3.888	3 × 3, 12 × 6	6	0	27.648	10.032.906.240	107.495.424	39.007.939.461.120
CS + GR	cS6 \| C6	142	31.104	3 × 3, 12 × 6	6	0	6.480	2.351.462.400	201.553.920	73.139.886.489.600
CS + JR / B2, GR / B13	S6 \| C6	143	15.552	3 × 3, 12 × 6	6	0	1.728	627.056.640	26.873.856	9.751.984.865.280
CS + GR / Banda 2, JR / B13	cS \| C6	144	15.552	3 × 3, 12 × 6	6	0	3.456	1.254.113.280	53.747.712	19.503.969.730.560
CS + JR	S \| C6	145	7.776	3 × 3, 12 × 6	6	0	13.824	5.016.453.120	107.495.424	39.007.939.461.120
(não trivial)									949.129.933.824	344.420.270.386.053.120
total									18.384.171.550.626.816	6.671.248.172.291.458.990.080

Observe que uma grade pode ser um ponto fixo de várias transformações simultaneamente; por exemplo, qualquer grade que tenha simetria de um quarto de volta também tem simetria de meia volta. A combinação de todas as transformações que fixam uma grade específica é o subgrupo estabilizador ("grupo de automorfismo") dessa grade.

Subgrupos de estabilizadores

Russell compilou uma lista de 122 classes de conjugação de subgrupos de estabilizadores não triviais "essencialmente diferentes" ("grupos de automorfismo"), junto com uma grade de exemplo, as classes de conjugação VPT no grupo, um conjunto de geradores e o número de grades essencialmente diferentes (órbitas) com essa classe de estabilizador. Até o isomorfismo, existem 26 estruturas de grupo diferentes. Existem 15 tamanhos diferentes de grupos de estabilizadores possíveis, listados na próxima seção.

Número de grades essencialmente equivalentes

Cada uma das grades essencialmente únicas pode ser analisada quanto a auto-semelhanças ("automorfismos") para avaliar a 'deficiência' no número de grades essencialmente equivalentes. Os resultados estão resumidos na tabela abaixo. No total, 560.151 das 5.472.730.538 grades essencialmente únicas (cerca de 1 / 10.000) têm uma forma de auto-similaridade (um estabilizador não trivial).

O tamanho da órbita (ou seja, o número de grades essencialmente equivalentes) pode ser calculado usando o teorema do estabilizador de órbita : é o tamanho do grupo de simetria sudoku dividido pelo tamanho do grupo estabilizador (ou "automorfismo"). Multiplicar o número de grades essencialmente únicas (o número de órbitas) com o tamanho da órbita dá o número total de grades com aquele tamanho de grupo estabilizador; o somatório fornece novamente o número total de grades sudoku possíveis. As grades "automórficas" têm órbitas menores, então a probabilidade de uma grade aleatória ter uma simetria cai: de cerca de 1 em 10.000 para grades essencialmente diferentes para cerca de 1 em 20.000 para todas as grades.

Número de grades de sudoku por tamanho do grupo do estabilizador
Tamanho do grupo estabilizador	Número de grades essencialmente únicas (número de órbitas)	Grades equivalentes (tamanho da órbita), ignorando a reclassificação	Número de grades, ignorando a reclassificação	Grades equivalentes (tamanho da órbita), incluindo reclassificação	Número total de grades
1	5.472.170.387	3.359.232	18.382.289.873.462.784	1.218.998.108.160	6.670.565.349.282.175.057.920
2	548.449	1.679.616	921.183.715.584	609.499.054.080	334.279.146.711.121.920
3	7.336	1.119.744	8.214.441.984	406.332.702.720	2.980.856.707.153.920
4	2.826	839.808	2.373.297.408	304.749.527.040	861.222.163.415.040
6	1.257	559.872	703.759.104	203.166.351.360	255.380.103.659.520
8	29	419.904	12.177.216	152.374.763.520	4.418.868.142.080
9	42	373.248	15.676.416	135.444.234.240	5.688.657.838.080
12	92	279.936	25.754.112	101.583.175.680	9.345.652.162.560
18	85	186.624	15.863.040	67.722.117.120	5.756.379.955.200
27	2	124.416	248.832	45.148.078.080	90.296.156.160
36	15	93.312	1.399.680	33.861.058.560	507.915.878.400
54	11	62.208	684.288	22.574.039.040	248.314.429.440
72	2	46.656	93.312	16.930.529.280	33.861.058.560
108	3	31.104	93.312	11.287.019.520	33.861.058.560
162	1	20.736	20.736	7.524.679.680	7.524.679.680
648	1	5.184	5.184	1.881.169.920	1.881.169.920
> 1	560.151		932.547.230.208		338.402.738.897.879.040
	5.472.730.538		18.383.222.420.692.992		6.670.903.752.021.072.936.960

Outras variantes

Os resultados da enumeração para muitas variantes do Sudoku foram calculados: eles estão resumidos abaixo.

Sudoku com restrições adicionais

A seguir estão todas as restrições do clássico Sudoku 3 × 3 (grade 9 × 9). Os nomes dos tipos não foram padronizados: clique nos links de atribuição para ver as definições.

Modelo	Número de grades	Atribuição	Verificado?
Sudoku quase mágico	248.832	Jones, Perkins e Roach	sim
Sudoku mágico	5.971.968	Stertenbrink	sim
Hipercubo	37.739.520	Stertenbrink	sim
3doku	104.015.259.648	Stertenbrink	sim
NRC Sudoku	6.337.174.388.428.800	Brouwer	sim
Sudoku X	55.613.393.399.531.520	Russell	sim
Grupos Disjuntos	201,105,135,151,764,480	Russell	sim

Sudoku com regiões retangulares

Na tabela, as dimensões do bloco são aquelas das regiões (por exemplo, 3 × 3 no Sudoku normal). A coluna "Rel Err" indica como uma aproximação simples baseada em contagens de banda calculadas (detalhadas nas seções abaixo) se compara à contagem de grade verdadeira: é uma subestimativa em todos os casos avaliados até agora. Os números para grades de bloco quadrado ( n ² × n ² ) estão listados em (sequência A107739 no OEIS ), e os números para 2 × n blocos (2 n × 2 n grades) estão listados em (sequência A291187 no OEIS ) .

Semelhante aos quadrados latinos , o número de grades de sudoku pode ser reduzido observando que há uma correspondência um a um com uma forma parcialmente padronizada, na qual o primeiro bloco tem os rótulos canônicos e tanto a linha superior quanto a coluna mais à esquerda são classificadas (tanto quanto as regras permitem, ou seja, dentro dos blocos e nas próprias pilhas / bandas). Para uma grade com blocos, cada grade reduzida corresponde a ${\ displaystyle R \ times C}$

{\ displaystyle (RC)! \ times (R!) ^ {C-1} (C-1)! \ times (C!) ^ {R-1} (R-1)! = (RC-1)! \ cdot R! ^ {C} \ cdot C! ^ {R}}

grades totais, que são 9! × 72 ² ou 1.881.169.920 para o Sudoku 3 × 3 normal. Essa redução é sempre um-para-um, ao contrário da ação do conjunto completo de transformações de preservação de validade ('simetrias de Sudoku') discutidas abaixo.

Dimensões		Número de grades completas				Husa. erro (Veja abaixo)	Fração de Quadrados latinos
Rede	Blocos	Exato	Magnitude	Atribuição	Verificado?	Husa. erro (Veja abaixo)	Fração de Quadrados latinos
4 × 4	2 × 2	288	2,8800 × 10 ²	vários	sim	-11,1%	0,5 × 10 ⁰
6 × 6	2 × 3	28.200.960	2.8201 × 10 ⁷	Pettersen	sim	-5,88%	3,5 × 10 ⁻²
8 × 8	2 × 4	29.136.487.207.403.520	2,9136 × 10 ¹⁶	Russell	sim	-1,91%	2,7 × 10 ⁻⁴
9 × 9	3 × 3	6.670.903.752.021.072.936.960	6,6709 × 10 ²¹	Stertenbrink	sim	-0,207%	1,2 × 10 ^-6
10 × 10	2 × 5	1.903.816.047.972.624.930.994.913.280.000	1,9038 × 10 ³⁰	Pettersen	sim	-0,375%	1,9 × 10 ^-7
12 × 12	3 × 4	81.171.437.193.104.932.746.936.103.027.318.645.818.654.720.000	8,1171 × 10 ⁴⁶	Pettersen / Silver	Não	-0,132%	desconhecido
12 × 12	2 × 6	38.296.278.920.738.107.863.746.324.732.012.492.486.187.417.600.000	3,8296 × 10 ⁴⁹	Pettersen	Não	-0,238%	desconhecido
15 × 15	3 × 5	desconhecido	Husa. 3,5086 × 10 ⁸⁴	Prata	Não	n / D	desconhecido
16 × 16	4 × 4	desconhecido	Husa. 5,9584 × 10 ⁹⁸	Prata	Não	n / D	desconhecido
20 × 20	4 × 5	desconhecido	Husa. 3,1764 × 10 ¹⁷⁵	Prata	Não	n / D	desconhecido
25 × 25	5 × 5	desconhecido	Husa. 4,3648 × 10 ³⁰⁸	Silver / Pettersen	Não	n / D	desconhecido

Um Sudoku resolvido permanecerá válido sob as ações das transformações de preservação de validade (ver também Jarvis). Contando cuidadosamente o número de grades invariantes para cada transformação, pode-se calcular o número de grades Sudoku essencialmente diferentes (veja acima). Métodos semelhantes foram aplicados a grades de sudoku de outras dimensões; os resultados estão resumidos na tabela abaixo. Para grades de blocos quadrados (sequência A109741 no OEIS ), a transformação de transposição pode ou não (ver abaixo) ser incluída no grupo VPT (simetria). O número de grades essencialmente diferentes pode ser estimado dividindo o número total de grades (conhecidas ou estimadas) pelo tamanho do grupo VPT (que é facilmente calculado), que essencialmente assume que o número de sudokus automórficos é insignificante. Os números de 2 × n blocos (2 N × 2 n grades) estão listadas em (sequência A291188 no OEIS ).

Dimensões		Grupo VPT			Número de grades essencialmente diferentes	Referência
Rede	Blocos	T	Tamanho	Conj. Aulas (sem rotular novamente)	Número de grades essencialmente diferentes	Referência
4 × 4	2 × 2	sim	128 × 4!		2
4 × 4	2 × 2	não	64 × 4!		3
6 × 6	2 × 3	não	3.456 × 6!	90	49	Jarvis / Russell, Pettersen
8 × 8	2 × 4	não	4.423.368 × 8!	400	1.673.187	Russell, Pettersen
9 × 9	3 × 3	sim	3.359.232 × 9!	275	5.472.730.538	Jarvis / Russell, Pettersen
9 × 9	3 × 3	não	1.679.616 × 9!	484	10.945.437.157	Jarvis / Russell, Pettersen
10 × 10	2 × 5	não	110.592.000 × 10!	1260	4.743.933.602.050.718	Pettersen / Russell
16 × 16	4 × 4	sim	(4!) ¹⁰ × 2 × 16!		Husa. 2,2458 × 10 ⁷¹	(estimativa explicada no texto)
16 × 16	4 × 4	não	(4!) ¹⁰ × 16!		Husa. 4,4916 × 10 ⁷¹	(estimativa explicada no texto)

Método de estimativa

O método de Kevin Kilfoil (generalizado por Pettersen) pode ser usado para estimar o número de grades concluídas usando o número de faixas e pilhas concluídas possíveis. O método afirma que as restrições de linha e coluna do Sudoku são, à primeira aproximação, condicionalmente independentes, dada a restrição de caixa. Isso dá a fórmula Kilfoil-Silver-Pettersen :

{\ displaystyle {\ mbox {Número de grades RC × RC com caixas R × C}} \ simeq {\ frac {(b_ {R, C}) ^ {C} \ times (b_ {C, R}) ^ { R}} {(RC)! ^ {RC}}}}

em que é o número de modos de enchimento de um R × RC banda de R horizontalmente adjacente R × C caixas (de modo equivalente, é o número de modos de enchimento de um RC × C pilha de C adjacentes verticalmente R × C caixas), e o denominador ( RC )! ^RC é o número de maneiras de preencher a grade enquanto satisfaz apenas as restrições da caixa. ${\ displaystyle b_ {R, C}}$ ${\ displaystyle b_ {C, R}}$

Conforme explicado por Pettersen: "É assim: Seja $X$ o espaço de -grades construídas por faixas de sudoku legais, mas sem atenção se as colunas seguem as regras de Sudoku. O tamanho de $X$ é . Seja $Y$ também o conjunto de grades construído por pilhas legais sem atenção colocada nas linhas, então é $#Y$ . As grades nxm-sudoku são então a interseção de $X$ e $Y.$ Um aleatório e são idênticos em uma determinada caixa com probabilidade e sob a suposição que essas probabilidades são independentes para cada caixa, chegamos à estimativa acima. " ${\ displaystyle (nm) \ times (nm)}$ ${\ displaystyle b (n, m) ^ {m}}$ ${\ displaystyle b (m, n) ^ {n}}$ ${\ displaystyle x (\ in X)}$ ${\ displaystyle y (\ in Y)}$ ${\ displaystyle (nm)!}$

Esta estimativa provou ser precisa em cerca de 0,2% para a grade clássica 9 × 9, e dentro de 1% para grades maiores para as quais os valores exatos são conhecidos (consulte a tabela acima).

Número de bandas

As fórmulas exatas para o número de bandas possíveis em uma grade de sudoku preenchida com blocos de tamanho R × C são conhecidas: ${\ displaystyle b_ {R, C}}$

Dimensões		Número de bandas	Atribuição	Verificado?
Banda	Blocos	Número de bandas	Atribuição	Verificado?
2 × 2 C	2 × C	${\ displaystyle b_ {2, C} = (2C)! (C!) ^ {2}}$	(resultado óbvio)	sim
3 × 3 C	3 × C	${\ displaystyle b_ {3, C} = (3C)! (C!) ^ {6} \ sum _ {k = 0} ^ {C} {C \ escolha k} ^ {3}}$ em que o somatório é conhecido como o $C$ ^th número Franel (sequência A000172 no OEIS )	Pettersen	sim
4 × 4 C	4 × C	${\ displaystyle b_ {4, C} = (4C)! (C!) ^ {12} \ sum _ {a, b, c} {\ left ({\ frac {C! ^ {2}} {a! b! c!}} \ cdot \ sum _ {k_ {12}, k_ {13}, k_ {14}, \ atop k_ {23}, k_ {24}, k_ {34}} {{a \ escolha k_ {12}} {b \ escolha k_ {13}} {c \ escolha k_ {14}} {c \ escolha k_ {23}} {b \ escolha k_ {24}} {a \ escolha k_ {34}}} \ direita) ^ {2}}}$ Onde: o summand exterior é tomada sobre toda a , b , c tal que 0≤ um , b , c e um + b + c = 2 C . o somatório interno é assumido sobre todos os k ₁₂ , k ₁₃ , k ₁₄ , k ₂₃ , k ₂₄ , k ₃₄ ≥ 0 de modo que k ₁₂ , k ₃₄ ≤ a e k ₁₃ , k ₂₄ ≤ b e k ₁₄ , k ₂₃ ≤ c e k ₁₂ + k ₁₃ + k ₁₄ = a - k ₁₂ + k ₂₃ + k ₂₄ = b - k ₁₃ + c - k ₂₃ + k ₃₄ = c - k ₁₄ + b - k ₂₄ + a - k ₃₄ = C A soma externa corresponde a uma divisão da banda em duas "sub-bandas" de 2 caixas cada; os números um , b e c descrevem a divisão e deve corresponder para ambas as sub-bandas, de modo que o summand pode ser quadrado. As variáveis de divisão são descritas como: " a é o número de símbolos nas linhas 1 e 2 nas primeiras caixas (ou seja, símbolos que estão na linha 1 na caixa 1 e na linha 2 na caixa 2 OU na linha 1 na caixa 2 e linha 2 na caixa 1). Será então também o número de símbolos nas linhas 3 e 4 nas primeiras duas caixas, bem como o número de símbolos nas linhas 1 e 2 nas duas últimas caixas, e o número de símbolos nas linhas 3 e 4 nas primeiras duas caixas. b é o número de símbolos nas linhas 1 e 3 nas duas primeiras caixas, juntamente com outras combinações como para a variável a . c é o número de símbolos nas linhas 1 e 4 nas duas primeiras caixas. " As contagens de soma interior o número de sub-bandas para um dado um , b , c especificação: "Entre os uma símbolos que se encontram na linha 1 e 2 na caixa 1 e 2, k ₁₂ contagens como muitos deles que se encontram na linha 1 na caixa 1 (e, portanto, também na linha 2 na caixa 2). Em geral, para i < j , entre os símbolos na linha i e j nas duas primeiras caixas, k _ij diz quantos deles estão na linha i na caixa 1 e a linha j na caixa 2. "	Pettersen	sim

Várias contagens de bandas conhecidas estão listadas abaixo. O algoritmo de Petersen, conforme implementado e aprimorado por Silver, divide a banda em sub-bandas, que são então agrupadas em classes de equivalência; é actualmente o mais rápido técnica conhecida para a avaliação exacta destes b _{R, C} .

Dimensões		Número de bandas	Atribuição	Verificado?
Banda	Blocos	Número de bandas	Atribuição	Verificado?
3 × 6	3 × 2	6! × 2! ⁶ × 10 = 460800	Pettersen (fórmula)
3 × 9	3 × 3	9! × 3! ⁶ × 56 = 9! × 2612736 = 948109639680 ≈9,4811 × 10 ¹¹ (44 classes de equivalência)	Vários
3 × 12	3 × 4	12! × 4! ⁶ × 346 = 31672366418991513600 ≈3,1672 × 10 ¹⁹	Stertenbrink	sim
3 × 15	3 × 5	15! × 5! ⁶ × 2252 ≈8,7934 × 10 ²⁷	Pettersen (fórmula)
(valores maiores de 3 × C podem ser facilmente calculados usando a fórmula fornecida acima)
4 × 8	4 × 2	8! × 2! ¹² × 5016 = 828396011520 ≈8,2840 × 10 ¹¹
4 × 12	4 × 3	12! × 3! ¹² × 2180544 = 2273614462643364849254400 ≈2,2736 × 10 ²⁴	Pettersen	sim
4 × 16	4 × 4	16! × 4! ¹² × 1273431960 ≈9,7304 × 10 ³⁸	Prata	sim
4 × 20	4 × 5	20! × 5! ¹² × 879491145024 ≈1,9078 × 10 ⁵⁵	Russell	sim
4 × 24	4 × 6	24! × 6! ¹² × 677542845061056 ≈8,1589 × 10 ⁷²	Russell	sim
4 × 28	4 × 7	28! × 7! ¹² × 563690747238465024 ≈4,6169 × 10 ⁹¹	Russell	sim
(cálculos de até 4 × 100 foram realizados pela Silver, mas não estão listados aqui)
5 × 10	5 × 2	10! × 2! ²⁰ × 364867776 ≈1,3883 × 10 ²¹ (355 classes de equivalência)		Não
5 × 15	5 × 3	15! × 3! ²⁰ × 324408987992064 ≈1,5510 × 10 ⁴²	Prata	Sim ^{mesmo autor, método diferente}
5 × 20	5 × 4	20! × 4! ²⁰ × 518910423730214314176 ≈5.0751 × 10 ⁶⁶	Prata	Sim ^{mesmo autor, método diferente}
5 × 25	5 × 5	25! × 5! ²⁰ × 1165037550432885119709241344 ≈6,9280 × 10 ⁹³	Pettersen / Silver	Não
5 × 30	5 × 6	30! × 6! ²⁰ × 3261734691836217181002772823310336 ≈1,2127 × 10 ¹²³	Pettersen / Silver	Não
5 × 35	5 × 7	35! × 7! ²⁰ × 10664509989209199533282539525535793414144 ≈1,2325 × 10 ¹⁵⁴	Pettersen / Silver	Não
5 × 40	5 × 8	40! × 8! ²⁰ × 39119312409010825966116046645368393936122855616 ≈4,1157 × 10 ¹⁸⁶	Pettersen / Silver	Não
5 × 45	5 × 9	45! × 9! ²⁰ × 156805448016006165940259131378329076911634037242834944 ≈2,9406 × 10 ²²⁰	Pettersen / Silver	Não
5 × 50	5 × 10	50! × 10! ²⁰ × 674431748701227492664421138490224315931126734765581948747776 ≈3,2157 × 10 ²⁵⁵	Pettersen / Silver	Não

6 × 12	6 × 2	12! × 2! ³⁰ × 9480675056071680 = 4876139207527966044188061990912000 ≈4,8761 × 10 ³³	Pettersen	Não

Quebra-cabeças

Número mínimo de dados

Sudokus comuns ( quebra-cabeças adequados ) têm uma solução única. Um Sudoku mínimo é um Sudoku do qual nenhuma pista pode ser removida, deixando-o um Sudoku adequado. Sudokus mínimos diferentes podem ter um número diferente de pistas. Esta seção discute o número mínimo de dados para quebra-cabeças adequados.

Sudoku comum

Um Sudoku com 17 pistas.

Um Sudoku com 17 pistas e simetria diagonal.

Um Sudoku com 18 pistas e simetria ortogonal.

Um Sudoku automórfico com 24 pistas e simetria geométrica completa.

Um Sudoku com 19 pistas e simetria ortogonal bidirecional.

Muitos Sudokus foram encontrados com 17 pistas, embora encontrá-los não seja uma tarefa trivial. Um artigo de Gary McGuire, Bastian Tugemann e Gilles Civario, lançado em 1 de janeiro de 2012, explica como foi provado por meio de uma pesquisa exaustiva no computador que o número mínimo de pistas em qualquer Sudoku adequado é 17, e isso foi confirmado independentemente em setembro de 2013 Alguns quebra-cabeças de 17 pistas com simetria diagonal foram fornecidos por Ed Russell, após uma pesquisa por meio de transformações de equivalência do banco de dados de Gordon Royle de quebra-cabeças de 17 pistas. Os quebra-cabeças de Sudoku com 18 pistas foram encontrados com simetria rotacional de 180 ° e outros com simetria ortogonal, embora não se saiba se este número de pistas é mínimo em ambos os casos. Os quebra-cabeças de Sudoku com 19 pistas foram encontrados com simetria ortogonal bidirecional e, novamente, não se sabe se esse número de pistas é mínimo para este caso.

Um Sudoku com 24 pistas, simetria diedral (simetria em ambos os eixos ortogonais, simetria rotacional de 90 °, simetria rotacional de 180 ° e simetria diagonal) é conhecida por existir e também é automórfico . Novamente aqui, não se sabe se este número de pistas é mínimo para esta classe de Sudoku. Acredita-se que o menor número de pistas em um Sudoku com simetria diagonal bidirecional seja 18, e em pelo menos um caso esse Sudoku também exibe automorfismo .

Entre as 5.472.730.538 grades de solução essencialmente diferentes , apenas 4 não têm um quebra-cabeça de 20 pistas - essas 4 grades têm um quebra-cabeça de 21 pistas.

Sudokus de outros tamanhos

Sudoku 4 × 4 (2 × 2): O menor número de pistas em qualquer Sudoku 4 × 4 é 4, dos quais existem 13 quebra-cabeças não equivalentes. (O número total de Sudokus mínimos não equivalentes deste tamanho é 36.)
6 × 6 (2 × 3) Sudoku: O menor número de pistas é 8.
8 × 8 (2 × 4) Sudoku: O menor número de pistas é 14.
10 × 10 (2 × 5) Sudoku: pelo menos um quebra-cabeça com 22 pistas foi criado. Não se sabe se este é o menor número possível.
12 × 12 (2 × 6) Sudoku: pelo menos um quebra-cabeça com 32 pistas foi criado. Não se sabe se este é o menor número possível.
12 × 12 (3 × 4) Sudoku: pelo menos um quebra-cabeça com 30 pistas foi criado. Não se sabe se este é o menor número possível.
15 × 15 (3 × 5) Sudoku: pelo menos um quebra-cabeça com 48 pistas foi criado. Não se sabe se este é o menor número possível.
16 × 16 (4 × 4) Sudoku: pelo menos um quebra-cabeça com 55 pistas foi criado. Não se sabe se este é o menor número possível.
25 × 25 (5 × 5) Sudoku: Um quebra-cabeça com 151 pistas foi criado. Não se sabe se este é o menor número possível.

Sudoku com restrições adicionais

Grupos Disjuntos: 11 pistas

Restrições adicionais (aqui, em Sudokus 3 × 3) levam a um número mínimo menor de pistas.

Grupos Disjuntos: alguns quebra-cabeças de 12 pistas foram demonstrados por Glenn Fowler. Mais tarde, também foram encontrados quebra-cabeças de 11 pistas. Não se sabe se este é o melhor possível.
Hipercubo: vários quebra-cabeças de 8 pistas foram demonstrados por Guenter Stertenbrink. Este é o melhor possível.
Magic Sudoku: um exemplo de 7 pistas foi fornecido por Guenter Stertenbrink. Não se sabe se este é o melhor possível.
Sudoku Anti-Knight: um exemplo de 8 pistas foi fornecido pelo usuário do Reddit u / _ryokousha. Este é o melhor possível.
Sudoku X: uma lista de 7193 quebra-cabeças de 12 pistas foi coletada por Ruud van der Werf. Não se sabe se este é o melhor possível.
NRC Sudoku: um exemplo de 11 pistas foi fornecido por Andries Brouwer. Não se sabe se este é o melhor possível.
2-Quasi-Magic Sudoku: um exemplo de 4 pistas foi fornecido por Tony Forbes. Suspeita-se que isso seja o melhor possível.

Sudoku com regiões irregulares

Os quebra-cabeças "Du-sum-oh" (também conhecidos como "local numérico geométrico") substituem as regiões 3 × 3 (ou R × C ) do Sudoku por formas irregulares de tamanho fixo. Bob Harris provou que é sempre possível a criação de ( N - 1) -clue du-Sum-ohs sobre um N × N grade, e construiu diversos exemplos. Johan de Ruiter provou que para qualquer N > 3 existem tilings Polyomino que não pode ser transformado em um quebra-cabeça Sudoku com N formas irregulares de tamanho N .

Soma do número da casa ("Killer Sudoku")

Na casa do número da soma (Samunampure), as restrições usuais de nenhum valor repetido em qualquer linha, coluna ou região se aplicam; além disso, regiões extras ("gaiolas") de vários tamanhos e formatos que não podem conter repetições estão presentes, com pistas que fornecem a soma dos dígitos dentro da gaiola (por exemplo, uma gaiola de 4 células com soma 10 deve consistir em valores 1,2,3 , 4 em alguma ordem). A cobertura celular mínima conhecida é de 18 células fornecidas por Philip Newman, e conjectura-se que seja a menor possível (um exemplo de 17 células implicaria em um sudoku clássico de 17 pistas atualmente desconhecido). O número mínimo de gaiolas conhecido é 7, também fornecido por Philip Newman; não se sabe se este é o menor número possível.

Uma variante no site de Miyuki Misawa substitui somas por relações: as pistas são símbolos = , < e > mostrando os valores relativos de (algumas, mas não todas) somas de regiões adjacentes. Ela demonstra um exemplo com apenas oito relações. Não se sabe se este é o melhor possível.

Número máximo de dados

Um Sudoku mínimo com 40 pistas.

Acredita-se que a maioria das pistas para um Sudoku mínimo sejam 40, das quais apenas duas são conhecidas. Se qualquer pista for removida de qualquer um desses Sudokus, o quebra-cabeça terá mais de uma solução (e, portanto, não será um Sudoku adequado). No trabalho para encontrar esses Sudokus, outros quebra-cabeças de pistas altas foram catalogados, incluindo mais de 6.500 milhões de quebra-cabeças mínimos com 36 pistas. Cerca de 2.600 Sudokus mínimos com 39 pistas também foram encontrados.

Se eliminar o requisito de exclusividade da solução, sabe-se da existência de pseudo-quebra-cabeças com 41 pistas, mas podem ser completados em mais de uma grade de solução. A remoção de qualquer pista aumenta o número de conclusões e, dessa perspectiva, nenhuma das 41 pistas é redundante. Com um pouco mais da metade da grade preenchida com dados (41 de 81 células), a exclusividade da restrição da solução ainda domina a restrição de minimalidade .

Quanto ao maior número de pistas possíveis em um Sudoku, embora ainda não reproduza uma solução única, é quatro a menos de uma grade completa (77). Se duas instâncias de dois números cada estão faltando e as células que devem ocupar são os cantos de um retângulo ortogonal, e exatamente duas dessas células estão dentro de uma região, há duas maneiras de adicionar os últimos dígitos (duas soluções).

Número de quebra-cabeças mínimos

O número de Sudokus mínimos (Sudokus nos quais nenhuma pista pode ser excluída sem perder a exclusividade da solução) não é conhecido com precisão. No entanto, as técnicas estatísticas combinadas com um gerador ( 'Estatísticas Imparcial de um CSP - Um Gerador de Polarização Controlada' ), mostram que existem aproximadamente (com erro relativo de 0,065%):

3,10 × 10 ³⁷ quebra-cabeças mínimos,
2,55 × 10 ²⁵ quebra-cabeças mínimos não essencialmente equivalentes.

Outros autores usaram métodos mais rápidos e calcularam estatísticas de distribuição precisas adicionais.

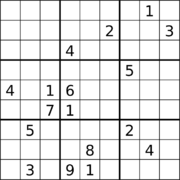
Restrições da geometria das pistas

Uma variedade de posições de pistas insuficientes para um Sudoku adequado.

Sudoku com um retângulo vazio de 30 células (5 x 6). (22 pistas)

Sudoku com nove grupos vazios. (22 pistas)

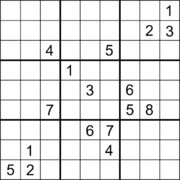
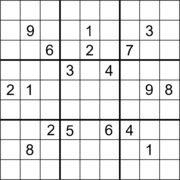
Foi conjecturado que nenhum Sudoku adequado pode ter pistas limitadas à gama de posições no espaço livre da primeira imagem acima. Acredita-se que o maior "buraco" ortogonal retangular (região sem pistas) em um Sudoku adequado seja um retângulo de 30 células (uma área retangular de 5 × 6). Um exemplo é um Sudoku com 22 pistas (segunda imagem). Acredita-se que o maior número total de grupos vazios (linhas, colunas e caixas) em um Sudoku seja nove. Um exemplo é um Sudoku com 3 linhas vazias, 3 colunas vazias e 3 caixas vazias (terceira imagem).

Sudokus automórfico

Uma grade de Sudoku é automórfica se puder ser transformada de uma maneira que leve de volta à grade original, quando a mesma transformação não levaria de volta à grade original. Um exemplo de uma grade que é automórfica seria uma grade que pode ser girada 180 graus, resultando em uma nova grade onde os novos valores das células são uma permutação da grade original. Sudokus automórficos são quebra-cabeças de Sudoku que resolvem em uma grade automórfica. Dois exemplos de Sudokus automórfico e uma grade automórfica são mostrados abaixo.

Um Sudoku automórfico com 18 pistas (simetria diagonal bidirecional)

Um Sudoku automórfico com 24 pistas (simetria diagonal bidirecional e simetria translacional)

A grade de solução "Mais Canônica" (648 automorfismos)

Número de grades essencialmente diferentes em cada
contagem de automorfismo
Auto- morfismos	Não. Grades	Auto- morfismos	Não. Grades
1	5472170387	18	85
2	548449	27	2
3	7336	36	15
4	2826	54	11
6	1257	72	2
8	29	108	3
9	42	162	1
12	92	648	1

Nos primeiros dois exemplos, observe que se o Sudoku for girado 180 graus e as pistas forem renomeadas com a permutação (123456789) -> (987654321), ele retornará ao mesmo Sudoku. Expresso de outra forma, esses Sudokus têm a propriedade de que cada par de pistas rotacionais de 180 graus (a, b) segue a regra (a) + (b) = 10.

Uma vez que esses Sudokus são automórficos, suas grades de soluções também são automórficas. Além disso, cada célula que é resolvida tem um parceiro simétrico que é resolvido com a mesma técnica (e o par teria a forma a + b = 10). Observe que no segundo exemplo, o Sudoku também exibe simetria translacional (ou de repetição); as pistas são agrupadas em grupos, com as pistas em cada grupo ordenadas sequencialmente (ou seja, n, n + 1, n + 2 e n + 3).

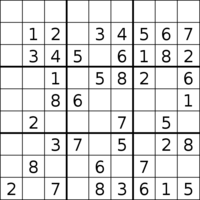
A terceira imagem é a grade da solução Mais Canonical . Esta grade tem 648 automorfismos e contribui para todos ~6,67 × 10 ²¹ grades de solução por fator de 1/648 em comparação com qualquer grade não automórfica.

Nestes exemplos, os automorfismos são fáceis de identificar, mas em geral o automorfismo nem sempre é óbvio. A tabela à direita mostra o número de grades de solução Sudoku essencialmente diferentes para todos os automorfismos existentes.

Detalhes de enumeração de grades distintas (9 × 9)

Foi desenvolvida uma técnica de enumeração baseada na geração de banda que é significativamente menos intensiva em termos de computação. A estratégia começa analisando as permutações da banda superior usadas em soluções válidas. Uma vez que as simetrias Band1 e a classe de equivalência para as soluções parciais são identificadas, as conclusões das duas bandas inferiores são construídas e contadas para cada classe de equivalência.

Contando as permutações da banda superior

1	2	3
4	5	6
7	8	9

O algoritmo Band1 procede da seguinte forma:

Escolha uma rotulação canônica dos dígitos atribuindo valores para B1 (consulte a grade) e calcule o restante das permutações de Band1 relativas a B1.
Calcule as permutações de B2, particionando os valores da célula B1 nos tripletos da linha B2 . A partir das combinações de trigêmeos, calcule as permutações de B2. Existem k = 0..3 maneiras de escolher:

Valores B1 r11 para B2 r22, o resto deve ir para r16,

Valores B1 r12 para B2 r23, o resto deve ir para r16,

Valores B1 r13 para B2 r21, o resto deve ir para r16, ou seja

{\ displaystyle {\ mbox {N combinações para B2}} = \ sum _ {k = 0} ^ {3} {{3 \ choose k} ^ {3}}}

(Esta expressão pode ser generalizada para qualquer variante de banda de caixa R × 3. (Pettersen). Assim, B2 contribui com 56 × 6 ³ permutações.

As escolhas para tripletos B3 são determinadas por linha pelos tripletos B1 B2. B3 sempre contribui com 6 ³ permutações.

As permutações para Band1 são $9! \times 56 \times 6 6 = 9! \times 2612736 \approx 9,48 \times 1011$ .

Detalhes de permutação da banda 1

Etiquetas triplas rBR (caixa / linha)

r	1	1
r	1	2
r	1	3

r	2	1
r	2	2
r	2	3

r	3	1
r	3	2
r	3	3

As permutações de B1 são o número de maneiras de renomear os 9 dígitos, 9! = 362880. Contar as permutações para B2 é mais complicado, porque as escolhas para B2 dependem dos valores em B1. (Esta é uma representação visual da expressão fornecida acima.) O cálculo condicional precisa de uma ramificação (sub-cálculo) para cada alternativa. Felizmente, existem apenas 4 casos para o tripleto B2 superior (r21): ele contém 0, 1, 2 ou 3 dos dígitos do tripleto B1 da linha do meio (r12). Uma vez que esta escolha da linha superior do B2 é feita, o resto das combinações do B2 são fixas. Os rótulos de tripleto de linha Band1 são mostrados à direita.

(Observação: as combinações condicionais tornam-se cada vez mais difíceis à medida que o cálculo avança na grade. Nesse ponto, o impacto é mínimo.)

Caso 0 Combinando Tripletos de Células

1	2	3
4	5	6
7	8	9

7	8	9
1	2	3
4	5	6

4	5	6
7	8	9
1	2	3

Caso 0: Sem sobreposição. As escolhas para os trigêmeos podem ser determinadas por eliminação.

r21 não pode ser r11 ou r12, então deve ser = r13; r31 deve ser = r12 etc.

O diagrama do Caso 0 mostra essa configuração, em que as células rosa são valores de trigêmeos que podem ser organizados em qualquer ordem dentro do trio. Cada trigêmeo tem 3! = 6 permutações. Os 6 tripletos contribuem com 6 ⁶ permutações.

Caso 3: Correspondência de 3 dígitos: tripleto r21 = r12. A mesma lógica do caso 0 se aplica, mas com um uso de trigêmeo diferente. O trio r22 deve ser = r13, etc. O número de permutações é novamente 6 ⁶ (Felgenhauer / Jarvis). Chame os casos 0 e 3 de caso de correspondência pura .

Caso 1 Match - Opções de células triplas

1	2	3
4	5	6
7	8	9

3	3	2
1	3	2
1	2	1

3	2	1
3	2	1
3	2	1

Caso 1: 1 correspondência para r21 de r12

No diagrama do Caso 1, as células B1 mostram valores canônicos, que são codificados por cores para mostrar sua distribuição por linha em tripletos B2. As cores refletem a distribuição, mas não a localização ou os valores. Para este caso: o tripleto da linha superior B2 (r21) tem 1 valor do trio do meio B1, as outras cores podem agora ser deduzidas. Por exemplo, a coloração do trio da linha inferior B2 (r23) é forçada por r21: os outros 2 valores do meio B1 devem ir para a parte inferior, etc. Preencha o número de opções B2 para cada cor, 3..1, começando no canto superior esquerdo. O código de cores B3 é omitido, uma vez que as escolhas de B3 são determinadas por linha por B1, B2. B3 sempre contribui com 3! permutações por tripleto de linha ou 6 ³ para o bloco.

Para B2, os valores do terceto podem aparecer em qualquer posição, portanto, um 3! o fator de permutação ainda se aplica, para cada trinca. No entanto, como alguns dos valores foram emparelhados em relação à sua origem, usar a opção bruta contagens superaria o número de permutações, devido à intercambiabilidade dentro do emparelhamento. As contagens de opções precisam ser divididas pelo tamanho permutado de seu agrupamento (2), aqui 2! = 2 (Ver ) O par em cada linha cancela os 2s para as contagens da opção B2, deixando uma contribuição B2 de $3$ $3$ $\times 6$ $3$ . A contribuição combinada B2 × B3 é $3$ $3$ $\times 6$ $6$ . ${\ displaystyle \ color {Azul} {n \ escolha k}}$

Caso 2 Match - Opções de células triplas

1	2	3
4	5	6
7	8	9

3	2	3
2	1	3
2	1	1

3	2	1
3	2	1
3	2	1

Caso 2: 2 correspondências para r21 de r12. A mesma lógica do caso 1 se aplica, mas com os agrupamentos de colunas de contagem da opção B2 invertidos. O caso 3 também contribui com 3 ³ × 6 ⁶ permutações.

Totalizando os 4 casos para Band1 B1..B3 dá $9! \times 2 \times (3 3 + 1) \times 6 6 = 9! 56 \times 6 6$ permutações.

Simetrias da banda 1 e classes de equivalência

Simetrias são usadas para reduzir o esforço computacional para enumerar as permutações Band1. Uma simetria é uma operação que preserva a qualidade de um objeto. Para uma grade de Sudoku, uma simetria é uma transformação cujo resultado também é uma grade válida. As seguintes simetrias se aplicam independentemente para a banda superior:

Os valores do bloco B1 podem ser etiquetados novamente, dando 9! permutações
Os blocos B1..3 podem ser trocados, com 3! = 6 permutações
As linhas 1..3 podem ser trocadas, com 3! = 6 permutações
Dentro de cada bloco, as 3 colunas podem ser trocadas, dando 3! ³ = 6 ³ permutações.

Combinadas, as simetrias resultam em 9! × 6 ⁵ = 362880 × 7776 permutações equivalentes para cada solução Band1.

Uma simetria define uma relação de equivalência , aqui, entre as soluções e particiona as soluções em um conjunto de classes de equivalência . As simetrias de linha, coluna e bloco Band1 dividem as permutações em (não menos que) 336 (56 × 6) classes de equivalência com (até) 6 ⁵ permutações em cada, e 9! renomear permutações para cada classe. ( Restrições mínimas / máximas se aplicam, uma vez que algumas permutações podem não produzir elementos distintos devido à reclassificação.) ${\ displaystyle 56 \ vezes 6 ^ {6}}$

Visto que a solução para qualquer membro de uma classe de equivalência pode ser gerada a partir da solução de qualquer outro membro, precisamos apenas enumerar as soluções para um único membro a fim de enumerar todas as soluções de todas as classes. Deixar

sb: ser uma permutação válida da banda superior
Sb = [sb]: ser uma classe de equivalência, em relação a sb e alguma relação de equivalência
Sb.z = | Sb | : o tamanho de Sb, seja o número de elementos sb (permutações) em [sb]
Sb.n: é o número de conclusões de Band2,3 para (qualquer) sb em Sb
{Sb}: é o conjunto de todas as classes de equivalência Sb em relação à relação de equivalência
{Sb} .z = | {Sb} | : ser o número de classes de equivalência

O número total de soluções N é então:

N =Sb.z × Sb.n

Simetria de permutação de solução e contagem

As simetrias Band1 (acima) são simetrias de permutação de solução definidas de forma que uma solução permutada também seja uma solução. Para o propósito de enumerar soluções, uma simetria de contagem para conclusão de grade pode ser usada para definir classes de equivalência de banda que geram um número mínimo de classes.

Contar partições de simetria permutações válidas de Band1 em classes que colocam as mesmas restrições de conclusão em bandas inferiores; todos os membros de uma classe de equivalência de simetria de contagem de banda devem ter o mesmo número de conclusões de grade, uma vez que as restrições de conclusão são equivalentes. As restrições de simetria de contagem são identificadas pelos tripletos da coluna Band1 (um conjunto de valores de coluna, sem ordem de elemento implícita). Usando a simetria de contagem de bandas, um conjunto gerador mínimo de 44 classes de equivalência foi estabelecido.

(1) Exemplo de banda 1

1	2	3
4	5	6
7	8	9

5	8	6
9	1	7
4	3	2

7	4	9
8	2	3
5	1	6

(2) Trigêmeos de coluna

1	2	3
4	5	6
7	8	9

4	1	2
5	3	6
9	8	7

5	1	3
7	2	6
8	4	9

(3) Col. Trigêmeos solicitados

1	2	3
4	5	6
7	8	9

1	3	5
2	6	7
4	9	8

1	2	4
3	6	5
8	7	9

A sequência a seguir demonstra o mapeamento de uma configuração de banda para uma classe de equivalência de simetria de contagem. Comece com uma configuração de banda válida (1). Crie trigêmeos de coluna ordenando os valores da coluna dentro de cada coluna. Esta não é uma faixa de Sudoku válida, mas coloca as mesmas restrições nas faixas inferiores do exemplo (2). Construir um ID de classe de equivalência a partir dos valores triplos das colunas B2, B3. Use trocas de coluna e caixa para obter o menor ID lexicográfico. A última figura mostra a ordem de coluna e caixa para o ID: 124 369 578 138 267 459. Todas as permutações Band1 com este ID de simetria de contagem terão o mesmo número de completações de grade que o exemplo original. Uma extensão deste processo pode ser usada para construir as maiores classes de equivalência de simetria de contagem de bandas (3).

Observe que, embora tripletos de coluna sejam usados para construir e identificar as classes de equivalência, os próprios membros da classe são as permutações Band1 válidas: o tamanho da classe (Sb.z) reflete permutações de tripletos de coluna compatíveis com os requisitos da solução One Rule . A simetria de contagem é uma propriedade de conclusão e se aplica apenas a uma grade parcial (banda ou pilha). A simetria da solução para soluções de preservação pode ser aplicada a grades parciais (faixas, pilhas) ou soluções de grade completa. Por último, observe que a simetria de contagem é mais restritiva do que a igualdade de contagem de conclusão numérica simples: duas bandas (distintas) pertencem à mesma classe de equivalência de simetria de contagem apenas se impõem restrições de conclusão equivalentes.

Detalhes de redução da banda 1

As simetrias agrupam objetos semelhantes em classes de equivalência . Dois números precisam ser distinguidos para classes de equivalência e simetrias de banda, conforme usado aqui, um terceiro:

o número de classes de equivalência ({Sb} .n).
a cardinalidade , tamanho ou número de elementos em uma classe de equivalência, que pode variar por classe (Sb.z)
o número de conclusões Band2,3 compatíveis com um membro de uma classe de equivalência Band1 (Sb.n)

As simetrias Band1 (6 ⁵ ) dividem as permutações válidas da Band1 (56 × 6 ⁶ ) em (não menos que) classes de equivalência de 336 (56 × 6) com (até) permutações cada. As ressalvas não inferior a e até são necessárias, uma vez que algumas combinações das transformações podem não produzir resultados distintos, quando a reetiquetagem é necessária (veja abaixo). Consequentemente, algumas classes de equivalência podem conter menos de 6 ⁵ permutações distintas e o número teórico mínimo de classes pode não ser alcançado. ${\ displaystyle 6 ^ {5}}$

Cada uma das permutações de Band1 válidas pode ser expandida (completada) em um número específico de soluções com as permutações de Band2,3. Em virtude de sua similaridade, cada membro de uma classe de equivalência terá o mesmo número de conclusões. Conseqüentemente, precisamos apenas construir as soluções para um membro de cada classe de equivalência e então multiplicar o número de soluções pelo tamanho da classe de equivalência. Ainda nos resta a tarefa de identificar e calcular o tamanho de cada classe de equivalência. O progresso adicional requer a aplicação hábil de técnicas computacionais para catalogar (classificar e contar) as permutações em classes de equivalência.

Felgenhauer / Jarvis catalogou as permutações Band1 usando IDs ordenados lexicográficos com base nos dígitos ordenados dos blocos B2,3. O bloco 1 usa uma atribuição de dígito canônico e não é necessário para um ID exclusivo. A identificação e ligação da classe de equivalência usa o ID mais baixo dentro da classe.

A aplicação das permutações de simetria (2 × 6 ² ) B2,3 produz 36288 (28 × 6 ⁴ ) classes de equivalência, cada uma com tamanho 72. Como o tamanho é fixo, o cálculo só precisa encontrar 36288 IDs de classe de equivalência. (Observação: neste caso, para qualquer permutação de Band1, a aplicação dessas permutações para obter o ID mais baixo fornece um índice para a classe de equivalência associada.)

A aplicação do resto das simetrias de bloco, coluna e linha proporcionou redução adicional, ou seja, alocação dos 36288 IDs em menos classes de equivalência maiores. Quando a rotulagem canônica B1 é perdida por meio de uma transformação, o resultado é rotulado novamente para o uso B1 canônico e, em seguida, catalogado sob este ID. Esta abordagem gerou 416 classes de equivalência, um pouco menos eficazes do que o limite mínimo teórico de 336 para uma redução total. A aplicação de padrões de simetria de contagem para dígitos emparelhados duplicados reduziu para 174 e depois para 71 classes de equivalência. A introdução de classes de equivalência com base na simetria de contagem de bandas (subsequente a Felgenhauer / Jarvis por Russell) reduziu as classes de equivalência a um conjunto gerador mínimo de 44.

A diversidade do ~2,6 × 10 ⁶ , 56 × 6 ⁶ As permutações de Band1 podem ser reduzidas a um conjunto de 44 classes de equivalência de Band1. Cada uma das 44 classes de equivalência pode ser expandida para milhões de soluções completas distintas, mas todo o espaço de solução tem uma origem comum nessas 44. As 44 classes de equivalência também desempenham um papel central em outras abordagens de enumeração, e a especulação retornará ao características das 44 classes quando as propriedades do quebra-cabeça são exploradas posteriormente.

Conclusão e resultados da faixa 2-3

A enumeração das soluções Sudoku divide-se em um estágio de configuração inicial e, em seguida, em dois loops aninhados. Inicialmente, todas as permutações de Band1 válidas são agrupadas em classes de equivalência, cada uma delas impõe uma restrição comum nas conclusões de Band2,3. Para cada uma das classes de equivalência de Band1, todas as soluções possíveis de Band2,3 precisam ser enumeradas. Um loop Band1 externo itera sobre as 44 classes de equivalência. No loop interno, todas as conclusões de banda inferior para cada classe de equivalência Band1 são encontradas e contadas.

O cálculo necessário para a busca de solução de banda inferior pode ser minimizado pelo mesmo tipo de aplicativo de simetria usado para Band1. Existem 6! (720) permutações para os 6 valores na coluna 1 de Band2,3. Aplicar as permutações de banda inferior (2) e linha dentro da banda (6 × 6) cria 10 classes de equivalência de tamanho 72. Neste ponto, completando 10 conjuntos de soluções para as 48 células restantes com uma descida recursiva, o algoritmo de retrocesso é viável com 2 PC de classe GHz, portanto, não é necessária nenhuma simplificação para realizar a enumeração. Usando esta abordagem, o número de maneiras de preencher uma grade de Sudoku em branco mostrou ser 6.670.903.752.021.072.936.960 (6,67 × 10 ²¹ ).

O resultado, conforme confirmado por Russell, também contém a distribuição de contagens de solução para as 44 classes de equivalência. Os valores listados são anteriores à aplicação do 9! fator para rotulagem e os dois 72 fatores (72 ² = 5184) para cada uma das permutações Stack 2,3 e Band2,3. O número de conclusões para cada classe é consistentemente na ordem de 100.000.000, enquanto o número de permutações Band1 abrangidas por cada classe varia de 4 a 3240. Dentro desta ampla faixa de tamanho, há claramente dois clusters. Classificadas por tamanho, as 33 classes mais baixas têm em média ~ 400 permutações / classe, enquanto as 11 mais altas têm a média de ~ 2100. A disparidade de consistência entre as distribuições de tamanho e número de conclusões ou a separação em dois clusters por tamanho ainda não foi examinada.

Veja também

Explosão combinatória (com resumo da contagem da grade do Sudoku em comparação com os quadrados latinos)
Links dançantes
Glossário de Sudoku
Sudokian
Código Sudoku

Referências

Leitura adicional

Rosenhouse, Jason ; Taalman, Laura (2011). Levando o Sudoku a sério: a matemática por trás do quebra-cabeça de lápis mais popular do mundo . Imprensa da Universidade de Oxford.

links externos

O algoritmo de mapa de diferenças de V. Elser também resolve Sudoku
Sudoku Puzzle - um Exercício de Programação de Restrições e Visual Prolog 7 por Carsten Kehler Holst (em Visual Prolog )
Sudoku Squares and Chromatic Polynomials de Herzberg e Murty, trata os quebra-cabeças de Sudoku como problemas de coloração de vértices na teoria dos grafos .

Languages

In other projects

Matemática do Sudoku - Mathematics of Sudoku

Visão geral

Contexto matemático

Sudokus das mesas de grupo

Variantes

Regiões retangulares

Sudokus Jigsaw

Soluções

Sudoku comum

Todas as soluções

Soluções essencialmente diferentes

Transformações de preservação de validade

O grupo de simetria sudoku

Pontos fixos e lema de Burnside

Subgrupos de estabilizadores

Número de grades essencialmente equivalentes

Outras variantes

Sudoku com restrições adicionais

Sudoku com regiões retangulares

Método de estimativa

Número de bandas

Quebra-cabeças

Número mínimo de dados

Sudoku comum

Sudokus de outros tamanhos

Sudoku com restrições adicionais

Sudoku com regiões irregulares

Soma do número da casa ("Killer Sudoku")

Número máximo de dados

Número de quebra-cabeças mínimos

Restrições da geometria das pistas

Sudokus automórfico

Detalhes de enumeração de grades distintas (9 × 9)

Contando as permutações da banda superior

Detalhes de permutação da banda 1

Simetrias da banda 1 e classes de equivalência

Simetria de permutação de solução e contagem

Detalhes de redução da banda 1

Conclusão e resultados da faixa 2-3

Veja também

Referências

Leitura adicional

links externos