Processo de decisão Markov - Markov decision process

Em matemática, um processo de decisão de Markov ( MDP ) é um processo de controle estocástico em tempo discreto . Ele fornece uma estrutura matemática para modelar a tomada de decisão em situações em que os resultados são parcialmente aleatórios e parcialmente sob o controle de um tomador de decisão. Os MDPs são úteis para estudar problemas de otimização resolvidos por meio da programação dinâmica . Os MDPs eram conhecidos pelo menos já na década de 1950; um corpo central de pesquisa sobre os processos de decisão de Markov resultou do livro de 1960 de Ronald Howard , Dynamic Programming and Markov Processes . Eles são usados ​​em muitas disciplinas, incluindo robótica , controle automático , economia e manufatura . O nome dos MDPs vem do matemático russo Andrey Markov , pois são uma extensão das cadeias de Markov .

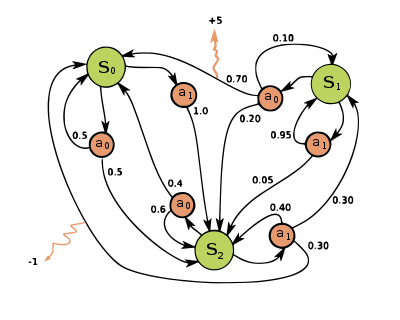
Em cada etapa de tempo, o processo está em algum estado e o tomador de decisão pode escolher qualquer ação que esteja disponível no estado . O processo responde na próxima etapa de tempo movendo-se aleatoriamente para um novo estado e dando ao tomador de decisão uma recompensa correspondente . ${\ displaystyle s}$${\ displaystyle a}$${\ displaystyle s}$${\ displaystyle s '}$${\ displaystyle R_ {a} (s, s ')}$

A probabilidade de o processo entrar em seu novo estado é influenciada pela ação escolhida. Especificamente, é fornecido pela função de transição de estado . Assim, o próximo estado depende do estado atual e da ação do tomador de decisão . Mas dado e , é condicionalmente independente de todos os estados e ações anteriores; em outras palavras, as transições de estado de um MDP satisfazem a propriedade de Markov . ${\ displaystyle s '}$${\ displaystyle P_ {a} (s, s ')}$${\ displaystyle s '}$${\ displaystyle s}$${\ displaystyle a}$${\ displaystyle s}$${\ displaystyle a}$

Os processos de decisão de Markov são uma extensão das cadeias de Markov ; a diferença é a adição de ações (permitindo a escolha) e recompensas (dando motivação). Por outro lado, se existir apenas uma ação para cada estado (por exemplo, "esperar") e todas as recompensas forem iguais (por exemplo, "zero"), um processo de decisão de Markov se reduz a uma cadeia de Markov.

Definição

Exemplo de um MDP simples com três estados (círculos verdes) e duas ações (círculos laranja), com duas recompensas (setas laranja).

Um processo de decisão de Markov é uma 4- tupla , onde: ${\ displaystyle (S, A, P_ {a}, R_ {a})}$

• ${\ displaystyle S}$é um conjunto de estados chamado de espaço de estado ,
• ${\ displaystyle A}$é um conjunto de ações chamado espaço de ação (alternativamente, é o conjunto de ações disponíveis a partir do estado ),${\ displaystyle A_ {s}}$${\ displaystyle s}$
• ${\ displaystyle P_ {a} (s, s ') = \ Pr (s_ {t + 1} = s' \ mid s_ {t} = s, a_ {t} = a)}$é a probabilidade de que a ação no estado no tempo levará ao estado no tempo ,${\ displaystyle a}$${\ displaystyle s}$${\ displaystyle t}$${\ displaystyle s '}$${\ displaystyle t + 1}$
• ${\ displaystyle R_ {a} (s, s ')}$é a recompensa imediata (ou recompensa imediata esperada) recebida após a transição de um estado para outro , devido à ação${\ displaystyle s}$${\ displaystyle s '}$${\ displaystyle a}$

Os espaços de estado e ação podem ser finitos ou infinitos, por exemplo, o conjunto de números reais . Alguns processos com estados e espaços de ação contáveis ​​infinitos podem ser reduzidos a outros com estados e espaços de ação finitos.

Uma função de política é um mapeamento (potencialmente probabilístico) do espaço de estado ( ) para o espaço de ação ( ). ${\ displaystyle \ pi}$${\ displaystyle S}$${\ displaystyle A}$

Objetivo de otimização

O objetivo em um processo de decisão de Markov é encontrar uma boa "política" para o tomador de decisão: uma função que especifica a ação que o tomador de decisão escolherá quando estiver no estado . Uma vez que um processo de decisão de Markov é combinado com uma política desta forma, isso corrige a ação para cada estado e a combinação resultante se comporta como uma cadeia de Markov (uma vez que a ação escolhida no estado é completamente determinada por e se reduz a uma matriz de transição de Markov) . ${\ displaystyle \ pi}$${\ displaystyle \ pi (s)}$${\ displaystyle s}$${\ displaystyle s}$${\ displaystyle \ pi (s)}$${\ displaystyle \ Pr (s_ {t + 1} = s '\ mid s_ {t} = s, a_ {t} = a)}$${\ displaystyle \ Pr (s_ {t + 1} = s '\ mid s_ {t} = s)}$

O objetivo é escolher uma política que maximize alguma função cumulativa das recompensas aleatórias, normalmente a soma descontada esperada ao longo de um horizonte potencialmente infinito: ${\ displaystyle \ pi}$

${\ displaystyle E \ left [\ sum _ {t = 0} ^ {\ infty} {\ gamma ^ {t} R_ {a_ {t}} (s_ {t}, s_ {t + 1})} \ right ]}$(onde escolhemos , ou seja, ações dadas pela política). E a expectativa é superada${\ displaystyle a_ {t} = \ pi (s_ {t})}$${\ displaystyle s_ {t + 1} \ sim P_ {a_ {t}} (s_ {t}, s_ {t + 1})}$

onde o fator de desconto é satisfatório , que geralmente é próximo a 1 (por exemplo, para alguma taxa de desconto r). Um fator de desconto menor motiva o tomador de decisão a favorecer a adoção de ações antecipadas, em vez de adiá-las indefinidamente. ${\ displaystyle \ \ gamma \}$${\ displaystyle 0 \ leq \ \ gamma \ \ leq \ 1}$${\ displaystyle \ gamma = 1 / (1 + r)}$

Uma política que maximiza a função acima é chamada de política ótima e geralmente é denotada . Um determinado MDP pode ter várias políticas ideais distintas. Por causa da propriedade de Markov, pode-se mostrar que a política ótima é uma função do estado atual, conforme assumido acima. ${\ displaystyle \ pi ^ {*}}$

Modelos de simulador

Em muitos casos, é difícil representar as distribuições de probabilidade de transição explicitamente. Nesses casos, um simulador pode ser usado para modelar o MDP implicitamente, fornecendo amostras das distribuições de transição. Uma forma comum de modelo MDP implícito é um simulador de ambiente episódico que pode ser iniciado de um estado inicial e produz um estado subsequente e recompensa toda vez que recebe uma entrada de ação. Dessa forma, podem ser produzidas trajetórias de estados, ações e recompensas, muitas vezes chamadas de episódios . ${\ displaystyle P_ {a} (s, s ')}$

Outra forma de simulador é um modelo generativo , um simulador de etapa única que pode gerar amostras do próximo estado e recompensar qualquer estado e ação. (Observe que este é um significado diferente do termo modelo generativo no contexto da classificação estatística.) Em algoritmos que são expressos usando pseudocódigo , é freqüentemente usado para representar um modelo generativo. Por exemplo, a expressão pode denotar a ação de amostragem do modelo gerador onde e são o estado e ação atuais e e são o novo estado e recompensa. Comparado a um simulador episódico, um modelo generativo tem a vantagem de poder gerar dados de qualquer estado, não apenas daqueles encontrados em uma trajetória. ${\ displaystyle G}$${\ displaystyle s ', r \ obtém G (s, a)}$${\ displaystyle s}$${\ displaystyle a}$${\ displaystyle s '}$${\ displaystyle r}$

Essas classes de modelo formam uma hierarquia de conteúdo de informação: um modelo explícito produz trivialmente um modelo generativo por meio de amostragem das distribuições, e a aplicação repetida de um modelo generativo produz um simulador episódico. Na direção oposta, só é possível aprender modelos aproximados por meio de regressão . O tipo de modelo disponível para um determinado MDP desempenha um papel significativo na determinação de quais algoritmos de solução são apropriados. Por exemplo, os algoritmos de programação dinâmica descritos na próxima seção requerem um modelo explícito, e a pesquisa em árvore de Monte Carlo requer um modelo generativo (ou um simulador episódico que pode ser copiado em qualquer estado), enquanto a maioria dos algoritmos de aprendizagem por reforço requerem apenas um simulador episódico .

Algoritmos

Soluções para MDPs com estados finitos e espaços de ação podem ser encontradas por meio de uma variedade de métodos, como programação dinâmica . Os algoritmos nesta seção se aplicam a MDPs com estados finitos e espaços de ação e probabilidades de transição e funções de recompensa explicitamente dadas, mas os conceitos básicos podem ser estendidos para lidar com outras classes de problemas, por exemplo, usando aproximação de função .

A família padrão de algoritmos para calcular políticas ideais para MDPs de estado e ação finitos requer armazenamento para duas matrizes indexadas por estado: valor , que contém valores reais, e política , que contém ações. No final do algoritmo, conterá a solução e conterá a soma descontada das recompensas a serem ganhas (em média) seguindo essa solução a partir do estado . ${\ displaystyle V}$ ${\ displaystyle \ pi}$${\ displaystyle \ pi}$${\ displaystyle V (s)}$${\ displaystyle s}$

O algoritmo tem duas etapas, (1) uma atualização de valor e (2) uma atualização de política, que são repetidas em alguma ordem para todos os estados até que nenhuma outra alteração ocorra. Ambos atualizam recursivamente uma nova estimativa da política ótima e valor de estado usando uma estimativa mais antiga desses valores.

${\ displaystyle V (s): = \ sum _ {s '} P _ {\ pi (s)} (s, s') \ left (R _ {\ pi (s)} (s, s ') + \ gamma V (s ') \ direita)}$

${\ displaystyle \ pi (s): = \ operatorname {argmax} _ {a} \ left \ {\ sum _ {s '} P (s' \ mid s, a) \ left (R (s '\ mid s , a) + \ gamma V (s ') \ right) \ right \}}$

Sua ordem depende da variante do algoritmo; pode-se também fazê-los para todos os estados de uma só vez ou estado por estado, e com mais freqüência para alguns estados do que para outros. Desde que nenhum estado seja permanentemente excluído de qualquer uma das etapas, o algoritmo acabará por chegar à solução correta.

Variantes notáveis

Iteração de valor

Na iteração de valor ( Bellman 1957 ), também chamada de indução reversa , a função não é usada; em vez disso, o valor de é calculado em sempre que necessário. Substituir o cálculo de no cálculo de dá a etapa combinada: ${\ displaystyle \ pi}$${\ displaystyle \ pi (s)}$${\ displaystyle V (s)}$${\ displaystyle \ pi (s)}$${\ displaystyle V (s)}$

${\ displaystyle V_ {i + 1} (s): = \ max _ {a} \ left \ {\ sum _ {s '} P_ {a} (s' | s) \ left (R_ {a} (s , s ') + \ gamma V_ {i} (s') \ right) \ right \},}$

onde está o número da iteração. A iteração de valor começa em e como uma estimativa da função de valor . Em seguida, itera, computando repetidamente para todos os estados , até convergir com o lado esquerdo igual ao lado direito (que é a " equação de Bellman " para este problema). O artigo de Lloyd Shapley de 1953 sobre jogos estocásticos incluiu como um caso especial o método de iteração de valor para MDPs, mas isso só foi reconhecido mais tarde. ${\ displaystyle i}$${\ displaystyle i = 0}$${\ displaystyle V_ {0}}$${\ displaystyle V_ {i + 1}}$${\ displaystyle s}$${\ displaystyle V}$

Iteração de política

Na iteração de política ( Howard 1960 ), a etapa um é executada uma vez e, em seguida, a etapa dois é repetida até convergir. Em seguida, a etapa um é executada novamente uma vez e assim por diante.

Em vez de repetir a etapa dois para a convergência, ela pode ser formulada e resolvida como um conjunto de equações lineares. Essas equações são obtidas simplesmente fazendo a equação da etapa dois. Assim, repetir a etapa dois para a convergência pode ser interpretado como resolver as equações lineares por Relaxamento (método iterativo)${\ displaystyle s = s '}$

Essa variante tem a vantagem de haver uma condição de parada definitiva: quando o array não muda durante a aplicação da etapa 1 a todos os estados, o algoritmo é concluído. ${\ displaystyle \ pi}$

A iteração de política é geralmente mais lenta do que a iteração de valor para um grande número de estados possíveis.

Iteração de política modificada

Na iteração de política modificada ( van Nunen 1976 ; Puterman & Shin 1978 ), a etapa um é executada uma vez e, em seguida, a etapa dois é repetida várias vezes. Em seguida, a etapa um é executada novamente uma vez e assim por diante.

Varredura priorizada

Nesta variante, as etapas são aplicadas preferencialmente a estados que são de alguma forma importantes - seja com base no algoritmo (houve grandes mudanças nesses estados ou em torno deles recentemente) ou com base no uso (esses estados estão próximos do estado inicial ou de outra forma de interesse para a pessoa ou programa que usa o algoritmo). ${\ displaystyle V}$${\ displaystyle \ pi}$

Extensões e generalizações

Um processo de decisão de Markov é um jogo estocástico com apenas um jogador.

Observabilidade parcial

A solução acima assume que o estado é conhecido quando a ação deve ser executada; caso contrário, não pode ser calculado. Quando essa suposição não é verdadeira, o problema é chamado de processo de decisão de Markov parcialmente observável ou POMDP. ${\ displaystyle s}$${\ displaystyle \ pi (s)}$

Um grande avanço nesta área foi fornecido por Burnetas e Katehakis em "Políticas adaptativas ótimas para processos de decisão de Markov". Neste trabalho, uma classe de políticas adaptativas que possuem propriedades uniformemente de taxa de convergência máxima para a recompensa total esperada no horizonte finito foram construídas sob as premissas de espaços de ação de estado finitos e irredutibilidade da lei de transição. Essas políticas prescrevem que a escolha de ações, em cada estado e período de tempo, deve ser baseada em índices que são inflações do lado direito das equações de otimização de recompensa média estimada.

Aprendizagem por reforço

A aprendizagem por reforço usa MDPs onde as probabilidades ou recompensas são desconhecidas.

Para este efeito, é útil definir uma função adicional, que corresponde a tomar a ação e, em seguida, continuar de forma otimizada (ou de acordo com qualquer política que se tenha atualmente): ${\ displaystyle a}$

${\ displaystyle \ Q (s, a) = \ sum _ {s '} P_ {a} (s, s') (R_ {a} (s, s ') + \ gamma V (s')). \ }$

Embora essa função também seja desconhecida, a experiência durante a aprendizagem é baseada em pares (junto com o resultado ; isto é, "Eu estava no estado e tentei fazer e aconteceu"). Assim, alguém tem um array e usa a experiência para atualizá-lo diretamente. Isso é conhecido como Q-learning . ${\ displaystyle (s, a)}$${\ displaystyle s '}$${\ displaystyle s}$${\ displaystyle a}$${\ displaystyle s '}$${\ displaystyle Q}$

A aprendizagem por reforço pode resolver os processos de decisão de Markov sem especificação explícita das probabilidades de transição; os valores das probabilidades de transição são necessários na iteração de valor e política. Na aprendizagem por reforço, em vez da especificação explícita das probabilidades de transição, as probabilidades de transição são acessadas por meio de um simulador que normalmente é reiniciado muitas vezes a partir de um estado inicial uniformemente aleatório. O aprendizado por reforço também pode ser combinado com a aproximação de funções para resolver problemas com um grande número de estados.

Autômatos de aprendizagem

Outra aplicação do processo MDP na teoria do aprendizado de máquina é chamada de autômatos de aprendizado. Este também é um tipo de aprendizado por reforço se o ambiente for estocástico. O primeiro artigo detalhado sobre autômatos de aprendizagem é pesquisado por Narendra e Thathachar (1974), que foram originalmente descritos explicitamente como autômatos de estados finitos . Semelhante ao aprendizado por reforço, um algoritmo de autômato de aprendizado também tem a vantagem de resolver o problema quando a probabilidade ou as recompensas são desconhecidas. A diferença entre autômatos de aprendizagem e Q-learning é que a primeira técnica omite a memória dos valores Q, mas atualiza a probabilidade de ação diretamente para encontrar o resultado do aprendizado. Autômatos de aprendizagem é um esquema de aprendizagem com uma prova rigorosa de convergência.

Na teoria dos autômatos de aprendizagem, um autômato estocástico consiste em:

• um conjunto x de possíveis entradas,
• um conjunto Φ = {Φ ₁ , ..., Φ _s } de possíveis estados internos,
• um conjunto α = {α ₁ , ..., α _r } de possíveis saídas, ou ações, com r ≤ s ,
• um vetor de probabilidade de estado inicial p (0) = ≪ p ₁ (0), ..., p _s (0) ≫,
• uma função computável A que, após cada etapa de tempo t, gera p ( t + 1) a partir de p ( t ), a entrada atual e o estado atual, e
• uma função G : Φ → α que gera a saída a cada passo de tempo.

Os estados de tal autômato correspondem aos estados de um " processo de Markov de parâmetro discreto de estado discreto ". A cada passo de tempo t = 0,1,2,3, ..., o autômato lê uma entrada de seu ambiente, atualiza P ( t ) para P ( t + 1) por A , escolhe aleatoriamente um estado sucessor de acordo com o probabilidades P ( t + 1) e produz a ação correspondente. O ambiente do autômato, por sua vez, lê a ação e envia a próxima entrada para o autômato.

Interpretação teórica da categoria

Além das recompensas, um processo de decisão de Markov pode ser entendido em termos da teoria da categoria . Ou seja, permitir que denotam a monóide livre com grupo gerador Uma . Deixe Dist denotar a categoria Kleisli da mônada Giry . Em seguida, um functor codifica tanto o conjunto S de estados e a função de probabilidade P . ${\ displaystyle (S, A, P)}$${\ displaystyle {\ mathcal {A}}}$${\ displaystyle {\ mathcal {A}} \ to \ mathbf {Dist}}$

Desta forma, os processos de decisão de Markov podem ser generalizados de monoides (categorias com um objeto) para categorias arbitrárias. Pode-se chamar o resultado de um processo de decisão de Markov dependente do contexto , porque se deslocam de um objeto a outro em mudanças do conjunto de ações disponíveis eo conjunto de estados possíveis. ${\ displaystyle ({\ mathcal {C}}, F: {\ mathcal {C}} \ to \ mathbf {Dist})}$${\ displaystyle {\ mathcal {C}}}$

Processo de decisão Markov em tempo contínuo

Em processos de decisão de Markov em tempo discreto, as decisões são feitas em intervalos de tempo discretos. No entanto, para processos de decisão Markov de tempo contínuo , as decisões podem ser feitas a qualquer momento que o tomador de decisão escolher. Em comparação aos processos de decisão de Markov de tempo discreto, os processos de decisão de Markov de tempo contínuo podem modelar melhor o processo de tomada de decisão para um sistema que possui dinâmica contínua , ou seja, a dinâmica do sistema é definida por equações diferenciais parciais (PDEs).

Definição

A fim de discutir o processo de decisão de Markov de tempo contínuo, apresentamos dois conjuntos de notações:

Se o espaço de estado e o espaço de ação são finitos,

• ${\ displaystyle {\ mathcal {S}}}$: Espaço de estado;
• ${\ displaystyle {\ mathcal {A}}}$: Espaço de ação;
• ${\ displaystyle q (i \ mid j, a)}$: , função de taxa de transição;${\ displaystyle {\ mathcal {S}} \ times {\ mathcal {A}} \ rightarrow \ triangle {\ mathcal {S}}}$
• ${\ displaystyle R (i, a)}$: , uma função de recompensa.${\ displaystyle {\ mathcal {S}} \ times {\ mathcal {A}} \ rightarrow \ mathbb {R}}$

Se o espaço de estado e espaço de ação são contínuos,

• ${\ displaystyle {\ mathcal {X}}}$: espaço de estado;
• ${\ displaystyle {\ mathcal {U}}}$: espaço de controle possível;
• ${\ displaystyle f (x, u)}$: , uma função de taxa de transição;${\ displaystyle {\ mathcal {X}} \ times {\ mathcal {U}} \ rightarrow \ triangle {\ mathcal {X}}}$
• ${\ displaystyle r (x, u)}$: , uma função de taxa de recompensa tal que , onde está a função de recompensa que discutimos no caso anterior.${\ displaystyle {\ mathcal {X}} \ times {\ mathcal {U}} \ rightarrow \ mathbb {R}}$${\ displaystyle r (x (t), u (t)) \, dt = dR (x (t), u (t))}$${\ displaystyle R (x, u)}$

Problema

Como os processos de decisão de Markov de tempo discreto, nos processos de decisão de Markov de tempo contínuo, queremos encontrar a política ou controle ideal que pode nos dar a recompensa integrada esperada ideal:

${\ displaystyle \ max \ operatorname {E} _ {u} \ left [\ left. \ int _ {0} ^ {\ infty} \ gamma ^ {t} r (x (t), u (t)) \ , dt \; \ right | x_ {0} \ right]}$

Onde ${\ displaystyle 0 \ leq \ gamma <1.}$

Formulação de programação linear

Se o espaço de estado e o espaço de ação forem finitos, poderíamos usar a programação linear para encontrar a política ótima, que foi uma das primeiras abordagens aplicadas. Aqui, consideramos apenas o modelo ergódico, o que significa que nosso MDP de tempo contínuo se torna uma cadeia de Markov de tempo contínuo ergódico sob uma política estacionária . Partindo desse pressuposto, embora o tomador de decisão possa tomar uma decisão a qualquer momento no estado atual, ele não poderia se beneficiar mais realizando mais de uma ação. É melhor para eles realizarem uma ação apenas no momento em que o sistema estiver fazendo a transição do estado atual para outro estado. Sob algumas condições, (para detalhes, verifique o Corolário 3.14 dos Processos de Decisão de Markov em Tempo Contínuo ), se nossa função de valor ótimo é independente do estado , teremos a seguinte desigualdade: ${\ displaystyle V ^ {*}}$${\ displaystyle i}$

${\ displaystyle g \ geq R (i, a) + \ sum _ {j \ in S} q (j \ mid i, a) h (j) \ quad \ forall i \ in S {\ text {e}} a \ em A (i)}$

Se existe uma função , então será a menor satisfazendo a equação acima. Para encontrar , poderíamos usar o seguinte modelo de programação linear: ${\ displaystyle h}$${\ displaystyle {\ bar {V}} ^ {*}}$${\ displaystyle g}$${\ displaystyle {\ bar {V}} ^ {*}}$

• Programa linear primordial (P-LP)

${\ displaystyle {\ begin {alinhado} {\ text {Minimize}} \ quad & g \\ {\ text {st}} \ quad & g- \ sum _ {j \ in S} q (j \ mid i, a) h (j) \ geq R (i, a) \, \, \ forall i \ in S, \, a \ in A (i) \ end {alinhado}}}$

• Programa linear duplo (D-LP)

${\ displaystyle {\ begin {align} {\ text {Maximize}} & \ sum _ {i \ in S} \ sum _ {a \ in A (i)} R (i, a) y (i, a) \\ {\ text {st}} & \ sum _ {i \ in S} \ sum _ {a \ in A (i)} q (j \ mid i, a) y (i, a) = 0 \ quad \ forall j \ in S, \\ & \ sum _ {i \ in S} \ sum _ {a \ in A (i)} y (i, a) = 1, \\ & y (i, a) \ geq 0 \ qquad \ forall a \ in A (i) {\ text {e}} \ forall i \ in S \ end {alinhados}}}$

${\ displaystyle y (i, a)}$é uma solução viável para o D-LP se não for nativa e satisfizer as restrições do problema D-LP. Uma solução viável para o D-LP é considerada uma solução ótima se ${\ displaystyle y (i, a)}$${\ displaystyle y ^ {*} (i, a)}$

${\ displaystyle {\ begin {alinhados} \ sum _ {i \ in S} \ sum _ {a \ in A (i)} R (i, a) y ^ {*} (i, a) \ geq \ sum _ {i \ in S} \ sum _ {a \ in A (i)} R (i, a) y (i, a) \ end {alinhado}}}$

para todas as soluções viáveis para o D-LP. Depois de encontrar a solução ideal , podemos usá-la para estabelecer as políticas ideais. ${\ displaystyle y (i, a)}$${\ displaystyle y ^ {*} (i, a)}$

Equação de Hamilton-Jacobi-Bellman

No MDP de tempo contínuo, se o espaço de estado e o espaço de ação são contínuos, o critério ótimo poderia ser encontrado resolvendo a equação diferencial parcial de Hamilton – Jacobi – Bellman (HJB) . Para discutir a equação HJB, precisamos reformular nosso problema

${\ displaystyle {\ begin {alinhados} V (x (0), 0) = {} & \ max _ {u} \ int _ {0} ^ {T} r (x (t), u (t)) \, dt + D [x (T)] \\ {\ text {st}} \ quad & {\ frac {dx (t)} {dt}} = f [t, x (t), u (t) ] \ end {alinhado}}}$

${\ displaystyle D (\ cdot)}$é a função de recompensa terminal, é o vetor de estado do sistema, é o vetor de controle do sistema que tentamos encontrar. mostra como o vetor de estado muda ao longo do tempo. A equação de Hamilton-Jacobi-Bellman é a seguinte: ${\ displaystyle x (t)}$${\ displaystyle u (t)}$${\ displaystyle f (\ cdot)}$

${\ displaystyle 0 = \ max _ {u} (r (t, x, u) + {\ frac {\ parcial V (t, x)} {\ parcial x}} f (t, x, u))}$

Poderíamos resolver a equação para encontrar o controle ideal , o que poderia nos dar a função de valor ideal${\ displaystyle u (t)}$ ${\ displaystyle V ^ {*}}$

Aplicativo

Os processos de decisão de Markov em tempo contínuo têm aplicações em sistemas de filas , processos epidêmicos e processos populacionais .

Notações alternativas

A terminologia e a notação para MDPs não estão totalmente definidas. Existem duas correntes principais - uma se concentra em problemas de maximização de contextos como economia, usando os termos ação, recompensa, valor e chamando o fator de desconto ou , enquanto a outra se concentra em problemas de minimização de engenharia e navegação, usando os termos controle, custo , custo para ir e chamando o fator de desconto . Além disso, a notação para a probabilidade de transição varia. ${\ displaystyle \ beta}$${\ displaystyle \ gamma}$${\ displaystyle \ alpha}$

neste artigo	alternativa	Comente
açao ${\ displaystyle a}$	ao controle ${\ displaystyle u}$
recompensa ${\ displaystyle R}$	custo ${\ displaystyle g}$	${\ displaystyle g}$ é o negativo de ${\ displaystyle R}$
valor ${\ displaystyle V}$	custo para ir ${\ displaystyle J}$	${\ displaystyle J}$ é o negativo de ${\ displaystyle V}$
política ${\ displaystyle \ pi}$	política ${\ displaystyle \ mu}$
fator de desconto ${\ displaystyle \ \ gamma \}$	fator de desconto ${\ displaystyle \ alpha}$
probabilidade de transição ${\ displaystyle P_ {a} (s, s ')}$	probabilidade de transição ${\ displaystyle p_ {ss '} (a)}$

Além disso, a probabilidade de transição é por vezes escrito , ou, raramente,${\ displaystyle \ Pr (s, a, s ')}$${\ displaystyle \ Pr (s '\ mid s, a)}$${\ displaystyle p_ {s's} (a).}$

Processos de decisão de Markov restritos

Os processos de decisão de Markov restritos (CMDPs) são extensões do processo de decisão de Markov (MDPs). Existem três diferenças fundamentais entre MDPs e CMDPs.

• Existem vários custos incorridos após a aplicação de uma ação em vez de uma.
• Os CMDPs são resolvidos apenas com programas lineares e a programação dinâmica não funciona.
• A política final depende do estado inicial.

Existem vários aplicativos para CMDPs. Recentemente, foi usado em cenários de planejamento de movimento em robótica.

Veja também

Referências

Leitura adicional

• Bellman., RE (2003) [1957]. Programação dinâmica (edição de brochura de Dover). Princeton, NJ: Princeton University Press. ISBN 978-0-486-42809-3.
• Bertsekas, D. (1995). Programação dinâmica e controle ideal . 2 . MA: Atena.
• Derman, C. (1970). Processos de decisão markovianos de estados finitos . Academic Press.
• Feinberg, EA; Shwartz, A., eds. (2002). Manual de processos de decisão de Markov . Boston, MA: Kluwer. ISBN 9781461508052.
• Guo, X .; Hernández-Lerma, O. (2009). Processos de decisão de Markov em tempo contínuo . Modelagem Estocástica e Probabilidade Aplicada. Springer. ISBN 9783642025464.
• Meyn, SP (2007). Técnicas de controle para redes complexas . Cambridge University Press. ISBN 978-0-521-88441-9. Arquivado do original em 19 de junho de 2010.O apêndice contém a versão resumida de "Meyn & Tweedie" . Arquivado do original em 18 de dezembro de 2012.
• Puterman., ML (1994). Processos de decisão de Markov . Wiley.
• Ross, SM (1983). Introdução à programação dinâmica estocástica (PDF) . Imprensa acadêmica.
• Sutton, RS; Barto, AG (2017). Aprendizagem por reforço: uma introdução . Cambridge, MA: The MIT Press.
• Tijms., HC (2003). Um primeiro curso em modelos estocásticos . Wiley. ISBN 9780470864289.

links externos

• Aprendendo a Resolver Processos de Decisão Markovianos por Satinder P. Singh