Desigualdade isoperimétrica - Isoperimetric inequality

Em matemática, a desigualdade isoperimétrica é uma desigualdade geométrica que envolve o perímetro de um conjunto e seu volume. No espaço -dimensional a desigualdade inferior delimita a área de superfície ou perímetro de um conjunto pelo seu volume de , ${\ displaystyle n}$${\ displaystyle \ mathbb {R} ^ {n}}$ ${\ displaystyle \ operatorname {por} (S)}$${\ displaystyle S \ subset \ mathbb {R} ^ {n}}$ ${\ displaystyle \ operatorname {vol} (S)}$

${\ displaystyle \ operatorname {per} (S) \ geq n \ operatorname {vol} (S) ^ {\ frac {n-1} {n}} \, \ operatorname {vol} (B_ {1}) ^ { \ frac {1} {n}}}$,

onde é uma esfera unitária . A igualdade é mantida apenas quando uma esfera está dentro . ${\ displaystyle B_ {1} \ subset \ mathbb {R} ^ {n}}$${\ displaystyle S}$${\ displaystyle \ mathbb {R} ^ {n}}$

Em um plano, isto é, quando , a desigualdade isoperimétrica relaciona o quadrado da circunferência de uma curva fechada e a área de uma região plana que ela envolve. Isoperimétrico significa literalmente "ter o mesmo perímetro ". Especificamente em , os estados de desigualdade isoperimétrica, para o comprimento L de uma curva fechada e a área A da região plana que ela envolve, que ${\ displaystyle n = 2}$${\ displaystyle \ mathbb {R} ^ {2}}$

${\ displaystyle L ^ {2} \ geq 4 \ pi A,}$

e essa igualdade se mantém se e somente se a curva for um círculo.

O problema isoperimétrico é determinar uma figura plana da maior área possível cujo limite tem um comprimento especificado. O problema de Dido intimamente relacionado pede uma região da área máxima limitada por uma linha reta e um arco curvilíneo cujos pontos finais pertencem a essa linha. Recebeu o nome de Dido , o lendário fundador e primeira rainha de Cartago . A solução para o problema isoperimétrico é dada por um círculo e já era conhecida na Grécia Antiga . No entanto, a primeira prova matematicamente rigorosa desse fato foi obtida apenas no século XIX. Desde então, muitas outras provas foram encontradas.

O problema isoperimétrico foi estendido de várias maneiras, por exemplo, para curvas em superfícies e para regiões em espaços de dimensões superiores. Talvez a manifestação física mais familiar da desigualdade isoperimétrica tridimensional seja a forma de uma gota d'água. Ou seja, uma gota normalmente assumirá uma forma redonda simétrica. Uma vez que a quantidade de água em uma gota é fixa, a tensão superficial força a gota a uma forma que minimiza a área da superfície da gota, ou seja, uma esfera redonda.

O problema isoperimétrico no plano

Se uma região não for convexa, um "dente" em seu limite pode ser "invertido" para aumentar a área da região, mantendo o perímetro inalterado.

Uma forma alongada pode ser tornada mais redonda, mantendo seu perímetro fixo e aumentando sua área.

O problema isoperimétrico clássico data da antiguidade. O problema pode ser formulado da seguinte forma: Dentre todas as curvas fechadas no plano do perímetro fixo, qual curva (se houver) maximiza a área de sua região fechada? Essa questão pode ser demonstrada como equivalente ao seguinte problema: Dentre todas as curvas fechadas no plano envolvendo uma área fixa, qual curva (se houver) minimiza o perímetro?

Esse problema está conceitualmente relacionado ao princípio da menor ação em física , na medida em que pode ser reafirmado: qual é o princípio de ação que engloba a maior área, com a maior economia de esforço? O filósofo e cientista do século XV, o cardeal Nicolau de Cusa , considerou a ação rotacional , o processo pelo qual um círculo é gerado, como o reflexo mais direto, no reino das impressões sensoriais, do processo pelo qual o universo é criado. O astrônomo e astrólogo alemão Johannes Kepler invocou o princípio isoperimétrico ao discutir a morfologia do sistema solar, em Mysterium Cosmographicum ( The Sacred Mystery of the Cosmos , 1596).

Embora o círculo pareça uma solução óbvia para o problema, provar esse fato é bastante difícil. O primeiro progresso em direção à solução foi feito pelo geômetro suíço Jakob Steiner em 1838, usando um método geométrico mais tarde denominado simetrização de Steiner . Steiner mostrou que, se existe uma solução, então deve ser o círculo. A prova de Steiner foi concluída mais tarde por vários outros matemáticos.

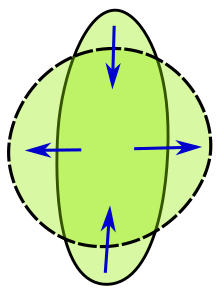
Steiner começa com algumas construções geométricas de fácil compreensão; por exemplo, pode ser mostrado que qualquer curva fechada envolvendo uma região que não é totalmente convexa pode ser modificada para incluir mais área, "invertendo" as áreas côncavas de modo que se tornem convexas. Pode-se ainda mostrar que qualquer curva fechada que não seja totalmente simétrica pode ser "inclinada" de modo que inclua mais área. A única forma perfeitamente convexa e simétrica é o círculo, embora isso, por si só, não represente uma prova rigorosa do teorema isoperimétrico (ver links externos).

Em um avião

A solução para o problema isoperimétrico é geralmente expressa na forma de uma desigualdade que relaciona o comprimento L de uma curva fechada e a área A da região plana que ela envolve. A desigualdade isoperimétrica afirma que

${\ displaystyle 4 \ pi A \ leq L ^ {2},}$

e que a igualdade se mantém se e somente se a curva for um círculo. A área de um disco de raio R é πR ² e a circunferência do círculo é 2 πR , então ambos os lados da inequação são iguais a 4 π ² R ² neste caso.

Dezenas de provas da desigualdade isoperimétrica foram encontradas. Em 1902, Hurwitz publicou uma curta prova usando a série de Fourier que se aplica a curvas retificáveis arbitrárias (não supostamente suaves). Uma prova directa elegante com base na comparação de uma curva fechada simples liso com um círculo apropriado foi dada por E. Schmidt em 1938. Ele usa apenas o comprimento de arco fórmula, expressão para a área de uma região plana do teorema do verde , e o Cauchy Desigualdade de Schwarz .

Para uma dada curva fechada, o quociente isoperimétrico é definido como a razão entre sua área e a do círculo com o mesmo perímetro. Isso é igual a

${\ displaystyle Q = {\ frac {4 \ pi A} {L ^ {2}}}}$

e a desigualdade isoperimétrica diz que Q ≤ 1. Equivalentemente, a razão isoperimétrica L ² / A é de pelo menos 4 π para cada curva.

O quociente isoperimétrico de um n -gon regular é

${\ displaystyle Q_ {n} = {\ frac {\ pi} {n \ tan {\ tfrac {\ pi} {n}}}}.}$

Let Ser uma curva fechada convexa regular suave. Então, a desigualdade isoperimétrica melhorada afirma o seguinte ${\ displaystyle C}$

${\ displaystyle L ^ {2} \ geqslant 4 \ pi A + 8 \ pi \ left | {\ widetilde {A}} _ {0.5} \ right |,}$

onde denotam o comprimento de , a área da região delimitada por e a área orientada da cáustica de Wigner de , respectivamente, e a igualdade se mantém se e somente se for uma curva de largura constante . ${\ displaystyle L, A, {\ widetilde {A}} _ {0,5}}$${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle C}$

Em uma esfera

Deixe C ser uma curva fechada de forma simples sobre uma esfera de raio 1. denota-se por L o comprimento de C e por uma área delimitada por C . A desigualdade isoperimétrica esférica afirma que

${\ displaystyle L ^ {2} \ geq A (4 \ pi -A),}$

e que a igualdade se mantém se e somente se a curva for um círculo. Existem, de fato, duas maneiras de medir a área esférica delimitada por uma curva fechada simples, mas a desigualdade é simétrica em relação à obtenção do complemento.

Essa desigualdade foi descoberta por Paul Lévy (1919), que também a estendeu para dimensões superiores e superfícies gerais.

No caso mais geral de raio R arbitrário , sabe-se que

${\ displaystyle L ^ {2} \ geq 4 \ pi A - {\ frac {A ^ {2}} {R ^ {2}}}.}$

No ${\ displaystyle \ mathbb {R} ^ {n}}$

A desigualdade isoperimétrica afirma que uma esfera tem a menor área de superfície por volume dado. Dado um conjunto limitado com área de superfície e volume , os estados de desigualdade isoperimétrica ${\ displaystyle S \ subset \ mathbb {R} ^ {n}}$ ${\ displaystyle \ operatorname {por} (S)}$ ${\ displaystyle \ operatorname {vol} (S)}$

${\ displaystyle \ operatorname {per} (S) \ geq n \ operatorname {vol} (S) ^ {\ frac {n-1} {n}} \, \ operatorname {vol} (B_ {1}) ^ { \ frac {1} {n}}}$,

onde está uma bola unitária . A igualdade é mantida quando é uma bola dentro . Sob restrições adicionais no conjunto (como convexidade , regularidade , limite suave ), a igualdade vale apenas para uma bola. Mas em geral a situação é mais complicada. O resultado relevante de Schmidt (1949 , Seção 20.7) (para uma prova mais simples, ver Baebler (1957) ) é esclarecido em Hadwiger (1957 , Seção 5.2.5) como segue. Um conjunto extremo consiste em uma bola e uma "coroa" que não contribui nem para o volume nem para a área de superfície. Ou seja, a igualdade é válida para um conjunto compacto se e somente se contém uma bola fechada tal que e. Por exemplo, a "coroa" pode ser uma curva. ${\ displaystyle B_ {1} \ subset \ mathbb {R} ^ {n}}$${\ displaystyle S}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle S}$${\ displaystyle S}$${\ displaystyle B}$${\ displaystyle \ operatorname {vol} (B) = \ operatorname {vol} (S)}$${\ displaystyle \ operatorname {por} (B) = \ operatorname {por} (S).}$

A prova da desigualdade segue diretamente da desigualdade de Brunn-Minkowski entre um conjunto e uma bola com raio , ie . Ao levar a desigualdade de Brunn-Minkowski ao poder , subtraindo de ambos os lados, dividindo-os por e tomando o limite como ( Osserman (1978) ; Federer (1969 , §3.2.43)). ${\ displaystyle S}$${\ displaystyle \ epsilon}$${\ displaystyle B _ {\ epsilon} = \ epsilon B_ {1}}$${\ displaystyle n}$${\ displaystyle \ operatorname {vol} (S)}$${\ displaystyle \ epsilon}$${\ displaystyle \ epsilon \ a 0.}$

Em geral ( Federer 1969 , §3.2.43), a desigualdade isoperimétrica afirma que para qualquer conjunto cujo fechamento tem medida de Lebesgue finita${\ displaystyle S \ subset \ mathbb {R} ^ {n}}$

${\ displaystyle n \, \ omega _ {n} ^ {\ frac {1} {n}} L ^ {n} ({\ bar {S}}) ^ {\ frac {n-1} {n}} \ leq M _ {*} ^ {n-1} (\ parcial S)}$

onde é o conteúdo de Minkowski ( n -1) -dimensional , L ⁿ é a medida de Lebesgue n- dimensional e ω _n é o volume da bola unitária em . Se a fronteira de S é retificável , então o conteúdo de Minkowski é a medida de Hausdorff ( n -1) -dimensional . ${\ displaystyle M _ {*} ^ {n-1}}$${\ displaystyle \ mathbb {R} ^ {n}}$

O n desigualdade isoperimétrica -dimensional é equivalente (para alisar suficientemente domínios) para a desigualdade Sobolev em com constante óptimo: ${\ displaystyle \ mathbb {R} ^ {n}}$

${\ displaystyle \ left (\ int _ {\ mathbb {R} ^ {n}} | u | ^ {\ frac {n} {n-1}} \ right) ^ {\ frac {n-1} {n }} \ leq n ^ {- 1} \ omega _ {n} ^ {- {\ frac {1} {n}}} \ int _ {\ mathbb {R} ^ {n}} | \ nabla u |}$

para todos . ${\ displaystyle u \ in W ^ {1,1} (\ mathbb {R} ^ {n})}$

Em variedades de Hadamard

Variedades Hadamard são variedades completas simplesmente conectadas com curvatura não positiva. Assim, eles generalizam o espaço euclidiano , que é uma variedade de Hadamard com curvatura zero. Na década de 1970 e início dos anos 80, Thierry Aubin , Misha Gromov , Yuri Burago e Viktor Zalgaller conjeturaram que a desigualdade isoperimétrica euclidiana ${\ displaystyle \ mathbb {R} ^ {n}}$

${\ displaystyle \ operatorname {per} (S) \ geq n \ operatorname {vol} (S) ^ {\ frac {n-1} {n}} \ operatorname {vol} (B_ {1}) ^ {\ frac {1} {n}}}$

vale para conjuntos limitados em variedades de Hadamard, que se tornou conhecida como a conjectura de Cartan-Hadamard . Na dimensão 2 isso já havia sido estabelecido em 1926 por André Weil , então aluno de Hadamard . Nas dimensões 3 e 4, a conjectura foi provada por Bruce Kleiner em 1992 e Chris Croke em 1984, respectivamente. ${\ displaystyle S}$

Em um espaço de medida métrica

A maior parte do trabalho sobre o problema isoperimétrico foi feito no contexto de regiões suaves em espaços euclidianos , ou mais geralmente, em variedades Riemannianas . No entanto, o problema isoperimétrico pode ser formulado em uma generalidade muito maior, usando a noção de conteúdo de Minkowski . Vamos ser um espaço de medida métrica : X é um espaço métrico com a métrica d , e μ é uma medida de Borel em X . A medida de limite , ou conteúdo de Minkowski , de um subconjunto mensurável A de X é definido como o lim inf${\ displaystyle (X, \ mu, d)}$

${\ displaystyle \ mu ^ {+} (A) = \ liminf _ {\ varepsilon \ to 0 +} {\ frac {\ mu (A _ {\ varepsilon}) - \ mu (A)} {\ varejpsilon}}, }$

Onde

${\ displaystyle A _ {\ varepsilon} = \ {x \ in X | d (x, A) \ leq \ varepsilon \}}$

é o ε- extensão de um .

O problema isoperimétrico em X pergunta quão pequeno pode ser para um dado µ ( A ). Se X é o plano euclidiano com a distância usual e a medida de Lebesgue, então essa questão generaliza o problema isoperimétrico clássico para regiões planas cuja fronteira não é necessariamente lisa, embora a resposta seja a mesma. ${\ displaystyle \ mu ^ {+} (A)}$

A função

${\ displaystyle I (a) = \ inf \ {\ mu ^ {+} (A) | \ mu (A) = a \}}$

é chamado de perfil isoperimétrico do espaço de medida métrica . Perfis isoperimétricos foram estudados para gráficos de Cayley de grupos discretos e para classes especiais de variedades Riemannianas (onde normalmente apenas regiões A com contorno regular são consideradas). ${\ displaystyle (X, \ mu, d)}$

Para gráficos

Na teoria dos grafos , as desigualdades isoperimétricas estão no cerne do estudo dos gráficos expansores , que são gráficos esparsos com fortes propriedades de conectividade. As construções expansoras geraram pesquisas em matemática pura e aplicada, com várias aplicações para a teoria da complexidade , projeto de redes de computadores robustas e a teoria de códigos de correção de erros .

Desigualdades isoperimétricas para gráficos relacionam o tamanho dos subconjuntos de vértices ao tamanho de seus limites, que geralmente é medido pelo número de arestas que saem do subconjunto (expansão da aresta) ou pelo número de vértices vizinhos (expansão do vértice). Para um gráfico e um número , a seguir estão dois parâmetros isoperimétricos padrão para gráficos. ${\ displaystyle G}$${\ displaystyle k}$

• O parâmetro isoperimétrico da borda:

${\ displaystyle \ Phi _ {E} (G, k) = \ min _ {S \ subseteq V} \ left \ {| E (S, {\ overline {S}}) |: | S | = k \ right \}}$

• O parâmetro isoperimétrico do vértice:

${\ displaystyle \ Phi _ {V} (G, k) = \ min _ {S \ subseteq V} \ left \ {| \ Gamma (S) \ setminus S |: | S | = k \ right \}}$

Aqui denota o conjunto de arestas saindo e denota o conjunto de vértices que têm um vizinho em . O problema isoperimétrico consiste em entender como os parâmetros e se comportam para famílias naturais de grafos. ${\ displaystyle E (S, {\ overline {S}})}$${\ displaystyle S}$${\ displaystyle \ Gamma (S)}$${\ displaystyle S}$${\ displaystyle \ Phi _ {E}}$${\ displaystyle \ Phi _ {V}}$

Exemplo: desigualdades isoperimétricas para hipercubos

O hipercubo -dimensional é o gráfico cujos vértices são todos vetores booleanos de comprimento , ou seja, o conjunto . Dois desses vetores são conectados por uma aresta em se eles forem iguais a um único bit flip, ou seja, sua distância de Hamming é exatamente um. A seguir estão as desigualdades isoperimétricas para o hipercubo booleano. ${\ displaystyle d}$ ${\ displaystyle Q_ {d}}$${\ displaystyle d}$${\ displaystyle \ {0,1 \} ^ {d}}$${\ displaystyle Q_ {d}}$

Desigualdade isoperimétrica de ponta

A desigualdade isoperimétrica de borda do hipercubo é . Esse limite é estreito, como é testemunhado por cada conjunto que é o conjunto de vértices de qualquer subcubo de . ${\ displaystyle \ Phi _ {E} (Q_ {d}, k) \ geq k (d- \ log _ {2} k)}$${\ displaystyle S}$${\ displaystyle Q_ {d}}$

Desigualdade isoperimétrica de vértice

O teorema de Harper diz que as bolas de Hamming têm o menor limite de vértice entre todos os conjuntos de um determinado tamanho. Bolas de Hamming são conjuntos que contêm todos os pontos de peso de Hamming, no máximo, e nenhum ponto de peso de Hamming maior do que algum número inteiro . Este teorema implica que qualquer conjunto com ${\ displaystyle r}$${\ displaystyle r + 1}$${\ displaystyle r}$${\ displaystyle S \ subseteq V}$

${\ displaystyle | S | \ geq \ sum _ {i = 0} ^ {r} {d \ escolher i}}$

satisfaz

${\ displaystyle | S \ cup \ Gamma (S) | \ geq \ sum _ {i = 0} ^ {r + 1} {d \ escolha i}.}$

Como um caso especial, considere definir tamanhos do formulário ${\ displaystyle k = | S |}$

${\ displaystyle k = {d \ escolher 0} + {d \ escolher 1} + \ pontos + {d \ escolher r}}$

para algum número inteiro . Então, o acima implica que o parâmetro isoperimétrico do vértice exato é ${\ displaystyle r}$

${\ displaystyle \ Phi _ {V} (Q_ {d}, k) = {d \ escolha r + 1}.}$

Desigualdade isoperimétrica para triângulos

A desigualdade isoperimétrica para triângulos em termos de perímetro pe área T afirma que

${\ displaystyle p ^ {2} \ geq 12 {\ sqrt {3}} \ cdot T,}$

com igualdade para o triângulo equilátero . Isso está implícito, por meio da desigualdade AM-GM , por uma desigualdade mais forte, que também foi chamada de desigualdade isoperimétrica para triângulos:

${\ displaystyle T \ leq {\ frac {\ sqrt {3}} {4}} (abc) ^ {\ frac {2} {3}}.}$

Veja também

• Teorema de Blaschke-Lebesgue
• Problema de Chaplygin
• Fluxo de encurtamento de curva
• Gráfico expansor
• Desigualdade isoperimétrica gaussiana
• Dimensão isoperimétrica
• Ponto isoperimétrico
• Lista de desigualdades de triângulo
• Teorema do separador planar
• Volume misto

Notas

Referências

links externos

• História do problema isoperimétrico na convergência
• Treiberg: várias provas da desigualdade isoperimétrica
• Teorema isoperimétrico no corte do nó