Gradiente descendente - Gradient descent

Tocar mídia

Gradiente descendente em 2D

O gradiente descendente é um algoritmo de otimização iterativa de primeira ordem para encontrar um mínimo local de uma função diferenciável . A ideia é dar passos repetidos na direção oposta do gradiente (ou gradiente aproximado) da função no ponto atual, porque esta é a direção de descida mais acentuada. Por outro lado, dar um passo na direção do gradiente levará a um máximo local dessa função; o procedimento é então conhecido como subida gradiente .

A descida gradiente é geralmente atribuída a Cauchy , que a sugeriu pela primeira vez em 1847. Hadamard propôs independentemente um método semelhante em 1907. Suas propriedades de convergência para problemas de otimização não linear foram estudadas pela primeira vez por Haskell Curry em 1944, com o método se tornando cada vez mais bem estudado e usado nas décadas seguintes, também frequentemente chamado de descida mais íngreme.

Descrição

Ilustração de gradiente descendente em uma série de conjuntos de níveis

A descida do gradiente é baseada na observação de que se a função multivariável é definida e diferenciável na vizinhança de um ponto , então diminui mais rapidamente se for na direção do gradiente negativo de at . Segue-se que, se ${\ displaystyle F (\ mathbf {x})}$${\ displaystyle \ mathbf {a}}$${\ displaystyle F (\ mathbf {x})}$${\ displaystyle \ mathbf {a}}$${\ displaystyle F}$${\ displaystyle \ mathbf {a}, - \ nabla F (\ mathbf {a})}$

${\ displaystyle \ mathbf {a} _ {n + 1} = \ mathbf {a} _ {n} - \ gamma \ nabla F (\ mathbf {a} _ {n})}$

por um pequeno o suficiente, então . Em outras palavras, o termo é subtraído porque queremos mover contra o gradiente, em direção ao mínimo local. Com esta observação em mente, começa-se com uma estimativa para um mínimo local de , e considera a sequência de tal forma que ${\ displaystyle \ gamma \ in \ mathbb {R} _ {+}}$${\ displaystyle F (\ mathbf {a_ {n}}) \ geq F (\ mathbf {a_ {n + 1}})}$${\ displaystyle \ gamma \ nabla F (\ mathbf {a})}$${\ displaystyle \ mathbf {a}}$${\ displaystyle \ mathbf {x} _ {0}}$${\ displaystyle F}$${\ displaystyle \ mathbf {x} _ {0}, \ mathbf {x} _ {1}, \ mathbf {x} _ {2}, \ ldots}$

${\ displaystyle \ mathbf {x} _ {n + 1} = \ mathbf {x} _ {n} - \ gamma _ {n} \ nabla F (\ mathbf {x} _ {n}), \ n \ geq 0.}$

Temos uma sequência monotônica

${\ displaystyle F (\ mathbf {x} _ {0}) \ geq F (\ mathbf {x} _ {1}) \ geq F (\ mathbf {x} _ {2}) \ geq \ cdots,}$

então, esperançosamente, a sequência converge para o mínimo local desejado. Observe que o valor do tamanho do passo pode mudar a cada iteração. Com certas suposições sobre a função (por exemplo, convexo e Lipschitz ) e escolhas particulares de (por exemplo, escolhido por meio de uma linha de pesquisa que satisfaça as condições de Wolfe ou o método Barzilai-Borwein mostrado a seguir), ${\ displaystyle (\ mathbf {x} _ {n})}$ ${\ displaystyle \ gamma}$${\ displaystyle F}$${\ displaystyle F}$ ${\ displaystyle \ nabla F}$ ${\ displaystyle \ gamma}$

${\ displaystyle \ gamma _ {n} = {\ frac {\ left | \ left (\ mathbf {x} _ {n} - \ mathbf {x} _ {n-1} \ right) ^ {T} \ left [\ nabla F (\ mathbf {x} _ {n}) - \ nabla F (\ mathbf {x} _ {n-1}) \ right] \ right |} {\ left \ | \ nabla F (\ mathbf {x} _ {n}) - \ nabla F (\ mathbf {x} _ {n-1}) \ right \ | ^ {2}}}}$

a convergência para um mínimo local pode ser garantida. Quando a função é convexa , todos os mínimos locais também são mínimos globais, portanto, neste caso, a descida do gradiente pode convergir para a solução global. ${\ displaystyle F}$

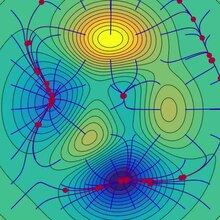
Este processo é ilustrado na imagem ao lado. Aqui, presume-se que está definido no plano e que seu gráfico tem uma forma de tigela . As curvas azuis são as curvas de nível , ou seja, as regiões nas quais o valor de é constante. Uma seta vermelha originada em um ponto mostra a direção do gradiente negativo naquele ponto. Observe que o gradiente (negativo) em um ponto é ortogonal à linha de contorno que passa por aquele ponto. Vemos que a descida do gradiente nos leva ao fundo da tigela, ou seja, ao ponto onde o valor da função é mínimo. ${\ displaystyle F}$${\ displaystyle F}$${\ displaystyle F}$

Uma analogia para entender a descida do gradiente

Nevoeiro nas montanhas

A intuição básica por trás da descida gradiente pode ser ilustrada por um cenário hipotético. Uma pessoa está presa nas montanhas e está tentando descer (ou seja, tentando encontrar o mínimo global). Há muita neblina, de modo que a visibilidade é extremamente baixa. Portanto, o caminho de descida da montanha não é visível, então eles devem usar as informações locais para encontrar o mínimo. Eles podem usar o método de descida gradiente, que envolve observar a inclinação da colina em sua posição atual e, em seguida, prosseguir na direção da descida mais acentuada (ou seja, descida). Se eles estivessem tentando encontrar o topo da montanha (ou seja, o máximo), eles seguiriam na direção da subida mais íngreme (ou seja, para cima). Usando este método, eles eventualmente encontrariam o caminho montanha abaixo ou possivelmente ficariam presos em algum buraco (isto é, mínimo local ou ponto de sela ), como um lago na montanha. No entanto, assuma também que a inclinação da colina não é imediatamente óbvia com a simples observação, mas requer um instrumento sofisticado de medição, que a pessoa tem no momento. Leva algum tempo para medir a inclinação da colina com o instrumento, portanto, eles devem minimizar o uso do instrumento se quiserem descer a montanha antes do pôr do sol. A dificuldade, então, é escolher a freqüência com que devem medir a inclinação do morro para não se desviarem.

Nessa analogia, a pessoa representa o algoritmo, e o caminho percorrido montanha abaixo representa a sequência de configurações de parâmetros que o algoritmo explorará. A inclinação da colina representa a inclinação da superfície de erro nesse ponto. O instrumento usado para medir a inclinação é a diferenciação (a inclinação da superfície de erro pode ser calculada tomando a derivada da função de erro quadrada naquele ponto). A direção que eles escolhem para viajar alinha-se com o gradiente da superfície de erro naquele ponto. A quantidade de tempo que eles viajam antes de fazer outra medição é o tamanho do passo.

Exemplos

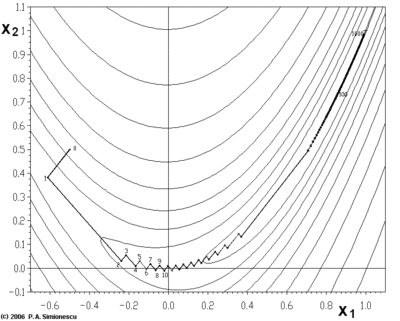
A descida gradiente tem problemas com funções patológicas, como a função de Rosenbrock mostrada aqui.

${\ displaystyle f (x_ {1}, x_ {2}) = (1-x_ {1}) ^ {2} +100 (x_ {2} -x_ {1} ^ {2}) ^ {2}. }$

A função Rosenbrock tem um vale estreito e curvo que contém o mínimo. O fundo do vale é muito plano. Por causa do vale plano curvo, a otimização está ziguezagueando lentamente com pequenos tamanhos de passo em direção ao mínimo. O Whiplash Gradient Descent resolve esse problema em particular.

A natureza ziguezagueante do método também é evidente abaixo, onde o método de gradiente descendente é aplicado a

${\ displaystyle F (x, y) = \ sin \ left ({\ frac {1} {2}} x ^ {2} - {\ frac {1} {4}} y ^ {2} +3 \ right ) \ cos \ left (2x + 1-e ^ {y} \ right).}$

Escolha do tamanho do passo e direção de descida

Visto que usar um tamanho de passo muito pequeno retardaria a convergência, e um tamanho muito grande levaria à divergência, encontrar um bom ajuste de é um problema prático importante. Philip Wolfe também defendeu o uso de "escolhas inteligentes da direção [da descida]" na prática. Embora usar uma direção que se desvia da direção de descida mais íngreme pode parecer contra-intuitivo, a ideia é que a inclinação menor pode ser compensada por ser sustentada por uma distância muito maior. ${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$

Para raciocinar sobre isso matematicamente, vamos usar uma direção e um tamanho de passo e considerar a atualização mais geral: ${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$

${\ displaystyle \ mathbf {a} _ {n + 1} = \ mathbf {a} _ {n} - \ gamma _ {n} \, \ mathbf {p} _ {n}}$.

Encontrar boas configurações de e requer um pouco de reflexão. Em primeiro lugar, gostaríamos que a direção da atualização apontasse para o declive. Matematicamente, deixar denotar o ângulo entre e , exige que Para dizer mais, precisamos de mais informações sobre a função objetivo que estamos otimizando. Sob a suposição bastante fraca que é continuamente diferenciável, podemos provar que: ${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$${\ displaystyle \ theta _ {n}}$${\ displaystyle \ nabla F (\ mathbf {a_ {n}})}$${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ cos \ theta _ {n}> 0.}$${\ displaystyle F}$

${\ displaystyle F (\ mathbf {a} _ {n + 1}) \ leq F (\ mathbf {a} _ {n}) - \ gamma _ {n} \ | \ nabla F (\ mathbf {a} _ {n}) \ | _ {2} \ | \ mathbf {p} _ {n} \ | _ {2} \ left [\ cos \ theta _ {n} - \ max _ {t \ in [0,1 ]} {\ frac {\ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n}) - \ nabla F (\ mathbf {a} _ {n}) \ | _ {2}} {\ | \ nabla F (\ mathbf {a} _ {n}) \ | _ {2}}} \ right]}$

( 1 )

Essa desigualdade implica que o valor pelo qual podemos ter certeza de que a função é diminuída depende de uma troca entre os dois termos entre colchetes. O primeiro termo entre colchetes mede o ângulo entre a direção da descida e o gradiente negativo. O segundo termo mede a rapidez com que o gradiente muda ao longo da direção de descida. ${\ displaystyle F}$

Em princípio, a desigualdade ( 1 ) pode ser otimizada sobre e para escolher um tamanho de passo e direção ideais. O problema é que avaliar o segundo termo entre colchetes requer avaliação , e avaliações de gradiente extra são geralmente caras e indesejáveis. Algumas maneiras de contornar esse problema são: ${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$${\ displaystyle \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n})}$

• Abandone os benefícios de uma direção de descida inteligente definindo e use a pesquisa de linha para encontrar um tamanho de degrau adequado , como um que satisfaça as condições de Wolfe .${\ displaystyle \ mathbf {p} _ {n} = \ nabla F (\ mathbf {a_ {n}})}$${\ displaystyle \ gamma _ {n}}$
• Assumindo que é duas vezes diferenciável, use seu Hessian para estimar Então escolha e otimizando a desigualdade ( 1 ).${\ displaystyle F}$${\ displaystyle \ nabla ^ {2} F}$${\ displaystyle \ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n}) - \ nabla F (\ mathbf {a} _ {n} ) \ | _ {2} \ approx \ | t \ gamma _ {n} \ nabla ^ {2} F (\ mathbf {a} _ {n}) \ mathbf {p} _ {n} \ |.}$${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$
• Supondo que seja Lipschitz , use sua constante de Lipschitz para vincular Então escolha e otimizando a desigualdade ( 1 ).${\ displaystyle \ nabla F}$${\ displaystyle L}$${\ displaystyle \ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ {n}) - \ nabla F (\ mathbf {a} _ {n} ) \ | _ {2} \ leq Lt \ gamma _ {n} \ | \ mathbf {p} _ {n} \ |.}$${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$
• Crie um modelo personalizado de para . Em seguida, escolha e otimizando a desigualdade ( 1 ).${\ displaystyle \ max _ {t \ in [0,1]} {\ frac {\ | \ nabla F (\ mathbf {a} _ {n} -t \ gamma _ {n} \ mathbf {p} _ { n}) - \ nabla F (\ mathbf {a} _ {n}) \ | _ {2}} {\ | \ nabla F (\ mathbf {a} _ {n}) \ | _ {2}}} }$${\ displaystyle F}$${\ displaystyle \ mathbf {p} _ {n}}$${\ displaystyle \ gamma _ {n}}$
• Sob suposições mais fortes sobre a função , como convexidade , técnicas mais avançadas podem ser possíveis.${\ displaystyle F}$

Normalmente, seguindo uma das receitas acima, a convergência para um mínimo local pode ser garantida. Quando a função é convexa , todos os mínimos locais também são mínimos globais, portanto, neste caso, a descida do gradiente pode convergir para a solução global. ${\ displaystyle F}$

Solução de um sistema linear

O algoritmo de descida mais íngreme aplicado ao filtro Wiener

O gradiente descendente pode ser usado para resolver um sistema de equações lineares

${\ displaystyle A \ mathbf {x} - \ mathbf {b} = 0}$

reformulado como um problema de minimização quadrática. Se a matriz do sistema for simétrica real e definida positivamente , uma função objetivo é definida como a função quadrática, com minimização de ${\ displaystyle A}$

${\ displaystyle F (\ mathbf {x}) = \ mathbf {x} ^ {T} A \ mathbf {x} -2 \ mathbf {x} ^ {T} \ mathbf {b},}$

de modo a

${\ displaystyle \ nabla F (\ mathbf {x}) = 2 (A \ mathbf {x} - \ mathbf {b}).}$

Para uma matriz real geral , mínimos quadrados lineares definem ${\ displaystyle A}$

${\ displaystyle F (\ mathbf {x}) = \ left \ | A \ mathbf {x} - \ mathbf {b} \ right \ | ^ {2}.}$

Nos mínimos quadrados lineares tradicionais para real e a norma euclidiana é usada, caso em que ${\ displaystyle A}$${\ displaystyle \ mathbf {b}}$

${\ displaystyle \ nabla F (\ mathbf {x}) = 2A ^ {T} (A \ mathbf {x} - \ mathbf {b}).}$

A minimização da pesquisa de linha , encontrando o tamanho do passo ideal localmente em cada iteração, pode ser realizada analiticamente para funções quadráticas, e fórmulas explícitas para o ótimo local são conhecidas. ${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$

Por exemplo, para uma matriz simétrica real e definida positivamente , um algoritmo simples pode ser o seguinte, ${\ displaystyle A}$

${\ displaystyle {\ begin {alinhado} & {\ text {repetir no ciclo:}} \\ & \ qquad \ mathbf {r}: = \ mathbf {b} - \ mathbf {Ax} \\ & \ qquad \ gamma: = {\ mathbf {r} ^ {\ mathsf {T}} \ mathbf {r}} / {\ mathbf {r} ^ {\ mathsf {T}} \ mathbf {Ar}} \\ & \ qquad \ mathbf {x}: = \ mathbf {x} + \ gamma \ mathbf {r} \\ & \ qquad {\ hbox {if}} \ mathbf {r} ^ {\ mathsf {T}} \ mathbf {r} { \ text {é suficientemente pequeno, então saia do loop}} \\ & {\ text {fim do loop de repetição}} \\ & {\ text {return}} \ mathbf {x} {\ text {como o resultado}} \ end {alinhado}}}$

Para evitar a multiplicação por duas vezes por iteração, notamos que implica , o que dá o algoritmo tradicional, ${\ displaystyle A}$${\ displaystyle \ mathbf {x}: = \ mathbf {x} + \ gamma \ mathbf {r}}$${\ displaystyle \ mathbf {r}: = \ mathbf {r} - \ gamma \ mathbf {Ar}}$

${\ displaystyle {\ begin {alinhado} & \ mathbf {r}: = \ mathbf {b} - \ mathbf {Ax} \\ & {\ text {repetir no ciclo:}} \\ & \ qquad \ gamma: = {\ mathbf {r} ^ {\ mathsf {T}} \ mathbf {r}} / {\ mathbf {r} ^ {\ mathsf {T}} \ mathbf {Ar}} \\ & \ qquad \ mathbf { x}: = \ mathbf {x} + \ gamma \ mathbf {r} \\ & \ qquad {\ hbox {if}} \ mathbf {r} ^ {\ mathsf {T}} \ mathbf {r} {\ text {é suficientemente pequeno, então saia do loop}} \\ & \ qquad \ mathbf {r}: = \ mathbf {r} - \ gamma \ mathbf {Ar} \\ & {\ text {fim do loop de repetição}} \\ & {\ text {return}} \ mathbf {x} {\ text {como o resultado}} \ end {alinhado}}}$

O método raramente é usado para resolver equações lineares, sendo o método do gradiente conjugado uma das alternativas mais populares. O número de iterações de descida de gradiente é comumente proporcional ao número da condição espectral da matriz do sistema (a proporção do máximo para os valores próprios mínimos de ) , enquanto a convergência do método do gradiente conjugado é normalmente determinada por uma raiz quadrada do número da condição, ou seja, , é muito mais rápido. Ambos os métodos podem se beneficiar do pré - condicionamento , onde a descida do gradiente pode exigir menos suposições sobre o pré-condicionador. ${\ displaystyle \ kappa (A)}$${\ displaystyle A}$${\ displaystyle A ^ {T} A}$

Solução de um sistema não linear

O gradiente descendente também pode ser usado para resolver um sistema de equações não lineares . Abaixo está um exemplo que mostra como usar a descida de gradiente para resolver três variáveis ​​desconhecidas, x ₁ , x ₂ e x ₃ . Este exemplo mostra uma iteração da descida do gradiente.

Considere o sistema não linear de equações

${\ displaystyle {\ begin {cases} 3x_ {1} - \ cos (x_ {2} x_ {3}) - {\ tfrac {3} {2}} = 0 \\ 4x_ {1} ^ {2} - 625x_ {2} ^ {2} + 2x_ {2} -1 = 0 \\\ exp (-x_ {1} x_ {2}) + 20x_ {3} + {\ tfrac {10 \ pi -3} {3 }} = 0 \ final {casos}}}$

Vamos apresentar a função associada

${\ displaystyle G (\ mathbf {x}) = {\ begin {bmatrix} 3x_ {1} - \ cos (x_ {2} x_ {3}) - {\ tfrac {3} {2}} \\ 4x_ { 1} ^ {2} -625x_ {2} ^ {2} + 2x_ {2} -1 \\\ exp (-x_ {1} x_ {2}) + 20x_ {3} + {\ tfrac {10 \ pi -3} {3}} \\\ end {bmatrix}},}$

Onde

${\ displaystyle \ mathbf {x} = {\ begin {bmatrix} x_ {1} \\ x_ {2} \\ x_ {3} \\\ end {bmatrix}}.}$

Pode-se agora definir a função objetivo

${\ displaystyle F (\ mathbf {x}) = {\ frac {1} {2}} G ^ {\ mathrm {T}} (\ mathbf {x}) G (\ mathbf {x}) = {\ frac {1} {2}} \ left [\ left (3x_ {1} - \ cos (x_ {2} x_ {3}) - {\ frac {3} {2}} \ right) ^ {2} + \ esquerda (4x_ {1} ^ {2} -625x_ {2} ^ {2} + 2x_ {2} -1 \ direita) ^ {2} + \ esquerda (\ exp (-x_ {1} x_ {2}) + 20x_ {3} + {\ frac {10 \ pi -3} {3}} \ direita) ^ {2} \ direita],}$

que tentaremos minimizar. Como um palpite inicial, vamos usar

${\ displaystyle \ mathbf {x} ^ {(0)} = \ mathbf {0} = {\ begin {bmatrix} 0 \\ 0 \\ 0 \\\ end {bmatrix}}.}$

Nós sabemos isso

${\ displaystyle \ mathbf {x} ^ {(1)} = \ mathbf {0} - \ gamma _ {0} \ nabla F (\ mathbf {0}) = \ mathbf {0} - \ gamma _ {0} J_ {G} (\ mathbf {0}) ^ {\ mathrm {T}} G ​​(\ mathbf {0}),}$

onde a matriz Jacobiana é dada por ${\ displaystyle J_ {G}}$

${\ displaystyle J_ {G} (\ mathbf {x}) = {\ begin {bmatrix} 3 & \ sin (x_ {2} x_ {3}) x_ {3} & \ sin (x_ {2} x_ {3} ) x_ {2} \\ 8x_ {1} & - 1250x_ {2} + 2 & 0 \\ - x_ {2} \ exp {(-x_ {1} x_ {2})} & - x_ {1} \ exp ( -x_ {1} x_ {2}) & 20 \\\ end {bmatrix}}.}$

Nós calculamos:

${\ displaystyle J_ {G} (\ mathbf {0}) = {\ begin {bmatrix} 3 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 20 \ end {bmatrix}}, \ qquad G (\ mathbf {0}) = {\ begin { bmatriz} -2,5 \\ - 1 \\ 10.472 \ end {bmatriz}}.}$

Assim

${\ displaystyle \ mathbf {x} ^ {(1)} = \ mathbf {0} - \ gamma _ {0} {\ begin {bmatrix} -7,5 \\ - 2 \\ 209,44 \ end {bmatrix}},}$

e

${\ displaystyle F (\ mathbf {0}) = 0,5 \ left ((- 2,5) ^ {2} + (- 1) ^ {2} + (10,472) ^ {2} \ right) = 58,456.}$

Uma animação mostrando as primeiras 83 iterações de descida de gradiente aplicadas a este exemplo. As superfícies são isosuperfícies da estimativa atual e as setas mostram a direção de descida. Devido a um tamanho de passo pequeno e constante, a convergência é lenta.${\ displaystyle F (\ mathbf {x} ^ {(n)})}$${\ displaystyle \ mathbf {x} ^ {(n)}}$

Agora, um adequado deve ser encontrado de modo que ${\ displaystyle \ gamma _ {0}}$

${\ displaystyle F \ left (\ mathbf {x} ^ {(1)} \ right) \ leq F \ left (\ mathbf {x} ^ {(0)} \ right) = F (\ mathbf {0}) .}$

Isso pode ser feito com qualquer um dos vários algoritmos de pesquisa de linha . Também se pode simplesmente adivinhar o que dá ${\ displaystyle \ gamma _ {0} = 0,001,}$

${\ displaystyle \ mathbf {x} ^ {(1)} = {\ begin {bmatrix} 0,0075 \\ 0,002 \\ - 0,20944 \\\ end {bmatrix}}.}$

Avaliar a função objetivo com este valor, produz

${\ displaystyle F \ left (\ mathbf {x} ^ {(1)} \ right) = 0,5 \ left ((- 2,48) ^ {2} + (- 1,00) ^ {2} + (6,28) ^ {2 } \ right) = 23,306.}$

A diminuição de para o valor da próxima etapa de ${\ displaystyle F (\ mathbf {0}) = 58.456}$

${\ displaystyle F \ left (\ mathbf {x} ^ {(1)} \ right) = 23,306}$

é uma diminuição considerável na função objetivo. Etapas adicionais reduziriam ainda mais seu valor, até que uma solução aproximada para o sistema fosse encontrada.

Comentários

A descida gradiente funciona em espaços de qualquer número de dimensões, mesmo em dimensões infinitas. No último caso, o espaço de busca é tipicamente um espaço de função , e calcula-se a derivada de Fréchet do funcional a ser minimizado para determinar a direção de descida.

Esse gradiente descendente funciona em qualquer número de dimensões (número finito, pelo menos) pode ser visto como uma consequência da desigualdade de Cauchy-Schwarz . Esse artigo prova que a magnitude do produto interno (ponto) de dois vetores de qualquer dimensão é maximizada quando eles são colineares. No caso de gradiente descendente, seria quando o vetor de ajustes de variáveis ​​independentes fosse proporcional ao vetor gradiente de derivadas parciais.

A descida gradiente pode levar muitas iterações para calcular um mínimo local com uma precisão necessária , se a curvatura em diferentes direções for muito diferente para a função dada. Para tais funções, o pré-condicionamento , que muda a geometria do espaço para moldar os conjuntos de nível de função como círculos concêntricos , cura a convergência lenta. No entanto, construir e aplicar o pré-condicionamento pode ser caro do ponto de vista computacional.

A descida do gradiente pode ser combinada com uma pesquisa de linha , encontrando o tamanho do passo ideal localmente em cada iteração. A execução da pesquisa de linha pode ser demorada. Por outro lado, o uso de um valor fixo pequeno pode resultar em convergência insuficiente. ${\ displaystyle \ gamma}$${\ displaystyle \ gamma}$

Métodos baseados no método de Newton e inversão do Hessiano usando técnicas de gradiente conjugado podem ser alternativas melhores. Geralmente, esses métodos convergem em menos iterações, mas o custo de cada iteração é maior. Um exemplo é o método BFGS que consiste em calcular a cada passo uma matriz pela qual o vetor gradiente é multiplicado para ir em uma direção "melhor", combinado com um algoritmo de busca linear mais sofisticado , para encontrar o "melhor" valor de For extremamente grandes problemas, onde os problemas de memória do computador dominam, um método de memória limitada como L-BFGS deve ser usado em vez de BFGS ou a descida mais íngreme. ${\ displaystyle \ gamma.}$

A descida gradiente pode ser vista como a aplicação do método de Euler para resolver equações diferenciais ordinárias a um fluxo de gradiente . Por sua vez, esta equação pode ser derivada como um controlador ideal para o sistema de controle com dado na forma de feedback . ${\ displaystyle x '(t) = - \ nabla f (x (t))}$${\ displaystyle x '(t) = u (t)}$${\ displaystyle u (t)}$${\ displaystyle u (t) = - \ nabla f (x (t))}$

Modificações

A descida gradiente pode convergir para um mínimo local e diminuir na vizinhança de um ponto de sela . Mesmo para minimização quadrática irrestrita, a descida gradiente desenvolve um padrão de zigue-zague de iterações subsequentes conforme o progresso das iterações, resultando em convergência lenta. Múltiplas modificações de gradiente descendente foram propostas para resolver essas deficiências.

Métodos de gradiente rápido

Yurii Nesterov propôs uma modificação simples que permite uma convergência mais rápida para problemas convexos e, desde então, foi generalizada. Para problemas de suavização irrestritos, o método é denominado método do gradiente rápido (FGM) ou método do gradiente acelerado (AGM). Especificamente, se a função diferenciável é convexa e é de Lipschitz , e não é assumido que é fortemente convexa , em seguida, o erro no valor objectivo gerado em cada passo através do método gradiente descendente será delimitada por . Usando a técnica de aceleração de Nesterov, o erro diminui em . Sabe-se que a taxa de diminuição da função de custo é ótima para métodos de otimização de primeira ordem. No entanto, existe a oportunidade de melhorar o algoritmo reduzindo o fator constante. O método de gradiente otimizado (OGM) reduz essa constante por um fator de dois e é um método de primeira ordem ideal para problemas de grande escala. ${\ displaystyle F}$${\ displaystyle \ nabla F}$${\ displaystyle F}$${\ displaystyle k}$ ${\ textstyle {\ mathcal {O}} \ left ({\ tfrac {1} {k}} \ right)}$${\ textstyle {\ mathcal {O}} \ left ({\ tfrac {1} {k ^ {2}}} \ right)}$${\ displaystyle {\ mathcal {O}} \ left ({k ^ {- 2}} \ right)}$

Para problemas restritos ou não suaves, o FGM de Nesterov é chamado de método do gradiente proximal rápido (FPGM), uma aceleração do método do gradiente proximal .

Método de impulso ou bola pesada

Tentando quebrar o padrão de zigue-zague da descida gradiente, o método momentum ou heavy ball usa um termo de momentum em analogia a uma bola pesada deslizando na superfície dos valores da função sendo minimizada, ou ao movimento de massa na dinâmica newtoniana por meio de um sistema viscoso meio em um campo de força conservador. A descida gradiente com momentum lembra a atualização da solução em cada iteração e determina a próxima atualização como uma combinação linear do gradiente e a atualização anterior. Para minimização quadrática irrestrita, um limite de taxa de convergência teórica do método de bola pesada é assintoticamente o mesmo que para o método de gradiente conjugado ideal .

Esta técnica é usada em gradiente descendente estocástico # Momentum e como uma extensão aos algoritmos de retropropagação usados ​​para treinar redes neurais artificiais .

Extensões

O gradiente descendente pode ser estendido para lidar com restrições , incluindo uma projeção no conjunto de restrições. Este método só é viável quando a projeção é eficientemente computável em um computador. Sob suposições adequadas, esse método converge. Este método é um caso específico do algoritmo forward-backward para inclusões monótonas (que inclui programação convexa e desigualdades variacionais ).

Veja também

Referências

Leitura adicional

• Boyd, Stephen ; Vandenberghe, Lieven (2004). "Minimização irrestrita" (PDF) . Otimização convexa . Nova York: Cambridge University Press. pp. 457–520. ISBN 0-521-83378-7.
• Chong, Edwin KP; Żak, Stanislaw H. (2013). "Métodos de gradiente" . Uma introdução à otimização (quarta edição). Hoboken: Wiley. pp. 131–160. ISBN 978-1-118-27901-4.
• Himmelblau, David M. (1972). "Procedimentos de minimização irrestritos usando derivados". Programação não linear aplicada . Nova York: McGraw-Hill. pp. 63–132. ISBN 0-07-028921-2.

links externos

• Usando gradiente descendente em C ++, Boost, Ublas para regressão linear
• Série de vídeos da Khan Academy discute a ascensão em gradiente
• Livro online que ensina gradiente descendente em contexto de rede neural profunda
• "Gradient Descent, How Neural Networks Learn" . 3Blue1Brown . 16 de outubro de 2017 - via YouTube .

arxiv.org/2108.1283