série de Fourier -Fourier series
| transformada de Fourier |
|---|
Uma série de Fourier ( / ˈ f ʊr i eɪ , -i ər / ) é uma expansão de uma função periódica em uma soma de funções trigonométricas . A série de Fourier é um exemplo de série trigonométrica , mas nem todas as séries trigonométricas são séries de Fourier. Ao expressar uma função como uma soma de senos e cossenos, muitos problemas envolvendo a função tornam-se mais fáceis de analisar porque as funções trigonométricas são bem compreendidas. Por exemplo, a série de Fourier foi usada pela primeira vez por Joseph Fourier para encontrar soluções para a equação do calor . Esta aplicação é possível porque as derivadas das funções trigonométricas se enquadram em padrões simples. A série de Fourier não pode ser usada para aproximar funções arbitrárias, porque a maioria das funções tem infinitos termos em suas séries de Fourier, e as séries nem sempre convergem . Funções bem comportadas, por exemplo, funções suaves , têm séries de Fourier que convergem para a função original. Os coeficientes da série de Fourier são determinados por integrais da função multiplicados por funções trigonométricas, descritas nas formas comuns da série de Fourier abaixo.
O estudo da convergência da série de Fourier concentra-se nos comportamentos das somas parciais , o que significa estudar o comportamento da soma à medida que mais e mais termos da série são somados. As figuras abaixo ilustram alguns resultados parciais da série de Fourier para os componentes de uma onda quadrada .
Uma onda quadrada (representada como o ponto azul) é aproximada por sua sexta soma parcial (representada como o ponto roxo), formada pela soma dos seis primeiros termos (representados como setas) da série de Fourier da onda quadrada. Cada seta começa na soma vertical de todas as setas à sua esquerda (ou seja, a soma parcial anterior).
As primeiras quatro somas parciais da série de Fourier para uma onda quadrada . À medida que mais harmônicos são adicionados, as somas parciais convergem para (tornam-se cada vez mais parecidas) com a onda quadrada.
As séries de Fourier estão intimamente relacionadas com a transformada de Fourier , que pode ser usada para encontrar as informações de frequência para funções que não são periódicas. Funções periódicas podem ser identificadas com funções em um círculo, por esta razão as séries de Fourier são o assunto da análise de Fourier em um círculo, geralmente denotado como ou . A transformada de Fourier também faz parte da Análise de Fourier , mas é definida para funções em
Desde a época de Fourier, muitas abordagens diferentes para definir e entender o conceito de série de Fourier foram descobertas, todas consistentes umas com as outras, mas cada uma enfatizando diferentes aspectos do tópico. Algumas das abordagens mais poderosas e elegantes são baseadas em ideias e ferramentas matemáticas que não estavam disponíveis na época de Fourier. Fourier definiu originalmente a série de Fourier para funções de valor real de argumentos reais e usou as funções seno e cosseno na decomposição. Muitas outras transformadas relacionadas a Fourier foram definidas desde então, estendendo sua ideia inicial para muitas aplicações e dando origem a uma área da matemática chamada análise de Fourier .
Formas comuns da série de Fourier
A série de Fourier pode ser representada de diferentes formas. A forma seno-coseno , forma exponencial e forma de fase de amplitude são expressas aqui para uma função periódica .

Forma seno-coseno
Os coeficientes da série de Fourier são definidos pelas integrais:
|
|
|
( Eq. 1 ) |
É notável que, é o valor médio da função . Esta é uma propriedade que se estende a transformações semelhantes, como a transformada de Fourier .
Com esses coeficientes definidos a série de Fourier é:
|
|
|
( Eq. 2 ) |
Muitos outros usam o símbolo, porque nem sempre é verdade que a soma da série de Fourier é igual a . Ele pode falhar em convergir totalmente ou convergir para algo diferente de . Embora essas situações possam ocorrer, suas diferenças raramente são um problema em ciência e engenharia, e os autores dessas disciplinas às vezes escrevem a Eq. 2 com substituído por .
O índice inteiro nos coeficientes da série de Fourier é o número de ciclos que o correspondente ou da série fazem no período da função . Portanto, os termos correspondentes a e têm:
- um comprimento de onda igual e com as mesmas unidades que .
- uma frequência igual a e tendo unidades recíprocas como .
Exemplo
Considere uma função dente de serra:
Neste caso, os coeficientes de Fourier são dados por
Pode-se mostrar que a série de Fourier converge para em todos os pontos onde é diferenciável e, portanto:
-
( Eq.8 )
Quando é um múltiplo ímpar de , a série de Fourier converge para 0, que é a meia-soma dos limites esquerdo e direito de s em . Este é um exemplo particular do teorema de Dirichlet para séries de Fourier.
Este exemplo leva a uma solução do problema de Basel .
Forma exponencial
É possível simplificar as integrais para os coeficientes da série de Fourier usando a fórmula de Euler .
Com as definições
|
|
|
( Eq. 3 ) |
Substituindo a equação Eq. 1 na Eq. 3 pode-se mostrar que:
Dados os coeficientes da série complexa de Fourier, é possível recuperar e das fórmulas
Com essas definições, a série de Fourier é escrita como:
|
|
|
( Eq. 4 ) |
Esta é a forma usual de generalização para funções com valores complexos. Valores negativos de correspondem à frequência negativa . (Veja também transformada de Fourier § Frequência negativa ).
Forma de fase de amplitude
A série de Fourier na forma de amplitude - fase é:
|
|
|
( Eq. 5 ) |
- Seu harmônico é .
- é a amplitude do harmônico e é sua mudança de fase .
- A frequência fundamental de é o termo para quando é igual a 1 e pode ser chamada de harmônica.
- às vezes é chamado de harmônico ou componente DC . É o valor médio de .
Claramente a Eq. 5 pode representar funções que são apenas uma soma de uma ou mais frequências harmônicas. O notável, para quem ainda não conhece esse conceito, é que ele também pode representar as frequências intermediárias e/ou funções não senoidais devido ao número potencialmente infinito de termos ( ) .

Os coeficientes e podem ser entendidos e derivados em termos de correlação cruzada entre e uma senóide na frequência . Para uma frequência geral e um intervalo de análise, a função de correlação cruzada:
|
|
|
( Eq. 6 ) |
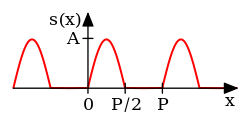
é essencialmente um filtro combinado , com modelo . Aqui denota Se é -periódico, é arbitrário, frequentemente escolhido para ser ou Mas, em geral, a série de Fourier também pode ser usada para representar uma função não periódica em apenas um intervalo finito, conforme ilustrado na Fig.1.
O máximo de é uma medida da amplitude da frequência na função , e o valor de no máximo determina a fase dessa frequência. A Figura 2 é um exemplo, onde é uma onda quadrada (não mostrada) e a frequência é o harmônico. É também um exemplo de derivação do máximo de apenas duas amostras, em vez de pesquisar a função inteira. Isso é possível por uma identidade trigonométrica :
Combinando isso com a Eq. 6 dá:
que introduz as definições de e . E notamos para referência posterior que e pode ser simplificado:
Portanto e são as coordenadas retangulares de um vetor com coordenadas polares e
Extensões para funções não periódicas
A série de Fourier também pode ser aplicada a funções que não são necessariamente periódicas. A extensão mais simples ocorre quando a função é definida apenas em um intervalo fixo . Nesse caso, as integrais que definem os coeficientes de Fourier podem ser obtidas nesse intervalo. Neste caso, todos os resultados de convergência serão os mesmos da extensão periódica de para toda a linha real. Em particular, pode acontecer que para uma função contínua haja uma descontinuidade na extensão periódica de at e . Neste caso, é possível ver o fenômeno de Gibbs nos pontos finais do intervalo.
Para funções que têm suporte compacto , o que significa que os valores de são definidos em todos os lugares, mas identicamente zero fora de algum intervalo fixo , a série de Fourier pode ser tomada em qualquer intervalo contendo o suporte .
Para ambos os casos acima, às vezes é desejável obter uma reflexão par ou ímpar da função ou estendê-la por zero no caso de a função ser definida apenas em um intervalo finito. Isso permite prescrever as propriedades desejadas para os coeficientes de Fourier. Por exemplo, ao tornar a função uniforme, você garante . Isso geralmente é conhecido como uma série de cossenos . Pode-se chegar similarmente a uma série de senos.
No caso em que a função não possui suporte compacto e é definida em toda a linha real, pode-se usar a transformada de Fourier . A série de Fourier pode ser tomada para uma versão truncada da função ou para a soma periódica .
Operador de Soma Parcial
Freqüentemente, ao descrever como as séries de Fourier se comportam, os autores introduzem o operador de soma parcial para uma função .
|
|
|
( Eq. 8 ) |
Onde estão os coeficientes de Fourier de . Ao contrário das séries em cálculo, é importante que as somas parciais sejam obtidas simetricamente para as séries de Fourier, caso contrário, os resultados da convergência podem não ser válidos.
Convergência
Uma prova de que uma série de Fourier é uma representação válida de qualquer função periódica (que satisfaça as condições de Dirichlet ) é vista em § Teorema de Fourier provando a convergência da série de Fourier .
Em aplicações de engenharia , a série de Fourier é geralmente considerada convergente, exceto em descontinuidades de salto, uma vez que as funções encontradas na engenharia são mais bem comportadas do que as funções encontradas em outras disciplinas. Em particular, se é contínua e a derivada de (que pode não existir em todos os lugares) é integrável ao quadrado, então a série de Fourier de converge absoluta e uniformemente para . Se uma função é integrável ao quadrado no intervalo , então a série de Fourier converge para a função em quase todos os lugares . É possível definir coeficientes de Fourier para funções ou distribuições mais gerais, caso em que a convergência pontual muitas vezes falha, e a convergência em norma ou convergência fraca é geralmente estudada.
Quatro somas parciais (série de Fourier) de comprimentos 1, 2, 3 e 4 termos, mostrando como a aproximação de uma onda quadrada melhora à medida que o número de termos aumenta (animação)
Quatro somas parciais (série de Fourier) de comprimentos 1, 2, 3 e 4 termos, mostrando como a aproximação de uma onda dente de serra melhora à medida que o número de termos aumenta (animação)
Exemplo de convergência para uma função um tanto arbitrária. Observe o desenvolvimento do "ringing" ( fenômeno de Gibbs ) nas transições de/para as seções verticais.
Outras notações comuns
A notação é inadequada para discutir os coeficientes de Fourier de várias funções diferentes. Portanto, é normalmente substituído por uma forma modificada da função ( , neste caso), como ou , e a notação funcional geralmente substitui a subscrição:
Na engenharia, particularmente quando a variável representa o tempo, a sequência de coeficientes é chamada de representação no domínio da frequência . Os colchetes costumam ser usados para enfatizar que o domínio dessa função é um conjunto discreto de frequências.
Outra representação de domínio de frequência comumente usada usa os coeficientes da série de Fourier para modular um pente de Dirac :
onde representa um domínio de frequência contínua. Quando variável tem unidades de segundos, tem unidades de hertz . Os "dentes" do pente são espaçados em múltiplos (ou seja, harmônicos ) de , que é chamado de frequência fundamental . pode ser recuperado a partir desta representação por uma transformada de Fourier inversa :
A função construída é, portanto, comumente chamada de transformada de Fourier , mesmo que a integral de Fourier de uma função periódica não seja convergente nas frequências harmônicas.
História
A série de Fourier é nomeada em homenagem a Jean-Baptiste Joseph Fourier (1768–1830), que fez importantes contribuições para o estudo das séries trigonométricas , após investigações preliminares de Leonhard Euler , Jean le Rond d'Alembert e Daniel Bernoulli . Fourier introduziu a série com o objetivo de resolver a equação do calor em uma placa de metal, publicando seus resultados iniciais em seu 1807 Mémoire sur la propagation de la chaleur dans les corps solides ( Tratado sobre a propagação do calor em corpos sólidos ) e publicando seu Théorie analytique de la chaleur ( Teoria analítica do calor ) em 1822. O Mémoire introduziu a análise de Fourier, especificamente a série de Fourier. Através da pesquisa de Fourier foi estabelecido o fato de que uma função arbitrária (no início, contínua e depois generalizada para qualquer função suave por partes ) pode ser representada por uma série trigonométrica. O primeiro anúncio desta grande descoberta foi feito por Fourier em 1807, perante a Academia Francesa . As primeiras ideias de decompor uma função periódica na soma de funções oscilantes simples datam do século III aC, quando antigos astrônomos propuseram um modelo empírico de movimentos planetários, baseado em deferentes e epiciclos .
A equação do calor é uma equação diferencial parcial . Antes do trabalho de Fourier, nenhuma solução para a equação do calor era conhecida no caso geral, embora soluções particulares fossem conhecidas se a fonte de calor se comportasse de maneira simples, em particular, se a fonte de calor fosse uma onda senoidal ou cosseno . Essas soluções simples agora são às vezes chamadas de autosoluções . A ideia de Fourier era modelar uma fonte de calor complicada como uma superposição (ou combinação linear ) de ondas senoidais e cosseno simples e escrever a solução como uma superposição das soluções próprias correspondentes . Essa superposição ou combinação linear é chamada de série de Fourier.
Do ponto de vista moderno, os resultados de Fourier são um tanto informais, devido à falta de uma noção precisa de função e integral no início do século XIX. Mais tarde, Peter Gustav Lejeune Dirichlet e Bernhard Riemann expressaram os resultados de Fourier com maior precisão e formalidade.
Embora a motivação original fosse resolver a equação do calor, mais tarde tornou-se óbvio que as mesmas técnicas poderiam ser aplicadas a uma ampla gama de problemas matemáticos e físicos, especialmente aqueles envolvendo equações diferenciais lineares com coeficientes constantes, para os quais as soluções próprias são sinusóides . A série Fourier tem muitas dessas aplicações em engenharia elétrica , análise de vibração , acústica , óptica , processamento de sinal , processamento de imagem , mecânica quântica , econometria , teoria de cascas , etc.
começos
Joseph Fourier escreveu:
Multiplicando ambos os lados por e , em seguida, integrando de a resulta:
— Joseph Fourier, Mémoire sur la propagation de la chaleur dans les corps solides . (1807)
Isso fornece imediatamente qualquer coeficiente a k da série trigonométrica para φ( y ) para qualquer função que tenha tal expansão. Funciona porque se φ tem tal expansão, então (sob suposições de convergência adequadas) a integral
Nessas poucas linhas, que se aproximam do formalismo moderno usado nas séries de Fourier, Fourier revolucionou tanto a matemática quanto a física. Embora séries trigonométricas semelhantes tenham sido usadas anteriormente por Euler , d'Alembert , Daniel Bernoulli e Gauss , Fourier acreditava que tais séries trigonométricas poderiam representar qualquer função arbitrária. Em que sentido isso é realmente verdade é uma questão um tanto sutil e as tentativas ao longo de muitos anos para esclarecer essa idéia levaram a importantes descobertas nas teorias de convergência , espaços funcionais e análise harmônica .
Quando Fourier apresentou um ensaio de competição posterior em 1811, o comitê (que incluía Lagrange , Laplace , Malus e Legendre , entre outros) concluiu: ...a maneira pela qual o autor chega a essas equações não está isenta de dificuldades e... sua análise para integrá-los ainda deixa a desejar no que se refere à generalidade e mesmo ao rigor .
A motivação de Fourier
A expansão em série de Fourier da função dente de serra (acima) parece mais complicada do que a fórmula simples , então não é imediatamente aparente por que alguém precisaria da série de Fourier. Embora existam muitas aplicações, a motivação de Fourier era resolver a
equação do calor . Por exemplo, considere uma placa de metal na forma de um quadrado cujos lados medem metros, com coordenadas . Se não houver fonte de calor dentro da placa, e se três dos quatro lados forem mantidos a 0 graus Celsius, enquanto o quarto lado, dado por , for mantido no gradiente de temperatura graus Celsius, para em , então pode-se mostrar que o distribuição estacionária de calor (ou a distribuição de calor após um longo período de tempo) é dada porAqui, sinh é a função seno hiperbólica . Esta solução da equação do calor é obtida multiplicando-se cada termo da Eq.6 por . Embora nossa função de exemplo pareça ter uma série de Fourier desnecessariamente complicada, a distribuição de calor não é trivial. A função não pode ser escrita como uma
expressão de forma fechada . Este método de resolver o problema do calor foi possível graças ao trabalho de Fourier.Animação complexa da série Fourier
Um exemplo da capacidade da série complexa de Fourier de traçar qualquer figura bidimensional fechada é mostrado na animação adjacente da série complexa de Fourier traçando a letra 'e' (para exponencial). Observe que a animação usa a variável 't' para parametrizar a letra 'e' no plano complexo, o que equivale a usar o parâmetro 'x' na subseção deste artigo sobre funções com valores complexos.
No backplane da animação, os vetores rotativos são agregados em uma ordem que alterna entre um vetor girando no sentido positivo (sentido anti-horário) e um vetor girando na mesma frequência, mas no sentido negativo (horário), resultando em um único traçado braço com muitos ziguezagues. Esta perspectiva mostra como a adição de cada par de vetores rotativos (um girando na direção positiva e outro girando na direção negativa) aproxima o traço anterior (mostrado como uma linha pontilhada cinza claro) da forma da letra 'e' .
No plano frontal da animação, os vetores rotativos são agregados em dois conjuntos, o conjunto de todos os vetores rotativos positivos e o conjunto de todos os vetores rotativos negativos (o componente não rotativo é dividido igualmente entre os dois), resultando em dois traçados braços girando em direções opostas. O pequeno círculo da animação denota o ponto médio entre os dois braços e também o ponto médio entre a origem e o ponto de rastreamento atual denotado por '+'. Essa perspectiva mostra como a série complexa de Fourier é uma extensão (adição de um braço) da série geométrica complexa que possui apenas um braço. Também mostra como os dois braços se coordenam. Por exemplo, como o ponto de rastreamento está girando na direção positiva, o braço de direção negativa permanece estacionado. Da mesma forma, quando o ponto de rastreamento está girando na direção negativa, o braço de direção positiva permanece estacionado.
Entre os planos traseiro e frontal da animação estão os trapézios rotativos cujas áreas representam os valores dos termos complexos da série de Fourier. Essa perspectiva mostra a amplitude, a frequência e a fase dos termos individuais da série complexa de Fourier em relação à soma da série convergente espacialmente para a letra 'e' nos planos traseiro e frontal. Os canais esquerdo e direito da faixa de áudio correspondem respectivamente aos componentes reais e imaginários do ponto de rastreamento atual '+', mas com frequência aumentada por um fator de 3536, de modo que a frequência fundamental da animação (n=1) é um tom de 220 Hz (A220 ).
Outras aplicações
Outra aplicação é resolver o problema de Basel usando o teorema de Parseval . O exemplo generaliza e pode-se calcular ζ (2 n ), para qualquer inteiro positivo n .
Tabela de séries comuns de Fourier
Alguns pares comuns de funções periódicas e seus coeficientes da série de Fourier são mostrados na tabela abaixo.
- designa uma função periódica com período .
- designe os coeficientes da série de Fourier (forma seno-cosseno) da função periódica .
| Domínio do tempo |
Trama | Domínio de frequência (forma seno-cosseno) |
Observações | Referência |
|---|---|---|---|---|
| Seno retificado de onda completa | ||||
| Seno retificado de meia onda | ||||
Tabela de propriedades básicas
Esta tabela mostra algumas operações matemáticas no domínio do tempo e o efeito correspondente nos coeficientes da série de Fourier. Notação:
- A conjugação complexa é indicada por um asterisco.
- designar funções periódicas
| Propriedade | Domínio do tempo | Domínio de frequência (forma exponencial) | Observações | Referência |
|---|---|---|---|---|
| Linearidade | ||||
| Reversão de tempo / reversão de frequência | ||||
| Conjugação de tempo | ||||
| Reversão de tempo e conjugação | ||||
| Parte real no tempo | ||||
| Parte imaginária no tempo | ||||
| Parte real em frequência | ||||
| Parte imaginária em frequência | ||||
| Deslocamento no tempo / Modulação na frequência | ||||
| Mudança na frequência / modulação no tempo |
Propriedades de simetria
Quando as partes reais e imaginárias de uma função complexa são decompostas em suas partes pares e ímpares , existem quatro componentes, indicados abaixo pelos subscritos RE, RO, IE e IO. E há um mapeamento um-para-um entre os quatro componentes de uma função de tempo complexa e os quatro componentes de sua transformada de frequência complexa:
A partir disso, várias relações são aparentes, por exemplo:
- A transformada de uma função de valor real ( s RE + s RO ) é a função par simétrica S RE + i S IO . Por outro lado, uma transformação simétrica implica um domínio de tempo de valor real.
- A transformada de uma função de valor imaginário ( i s IE + i s IO ) é a função simétrica ímpar S RO + i S IE , e o inverso é verdadeiro.
- A transformada de uma função par simétrica ( s RE + i s IO ) é a função de valor real S RE + S RO , e o inverso é verdadeiro.
- A transformada de uma função de simetria ímpar ( s RO + i s IE ) é a função de valor imaginário i S IE + i S IO , e o inverso é verdadeiro.
Outras propriedades
Lema de Riemann-Lebesgue
Se é
integrável , , e Este resultado é conhecido como lema de Riemann–Lebesgue .teorema de parval
Se pertence a (periódica sobre um intervalo de comprimento ) então
:Se pertence a (periódico sobre um intervalo de comprimento ), e é de comprimento finito, então :
para , então
e para , então
teorema de plancherel
Se são coeficientes e então existe uma única função tal que para cada .
teoremas de convolução
Dadas funções periódicas, e com coeficientes da série de Fourier e
- O produto pontual : também é -periódico, e seus coeficientes da série de Fourier são dados pela convolução discreta das sequências e :
- A convolução periódica : também é -periódico, com coeficientes da série de Fourier :
- Uma sequência duplamente infinita em é a sequência de coeficientes de Fourier de uma função em se e somente se for uma convolução de duas sequências em . Ver
Propriedade derivada
Dizemos que pertence a se é uma função 2 π -periódica na qual é diferenciável no tempo, e sua derivada é contínua.
- Se , então os coeficientes de Fourier da derivada podem ser expressos em termos dos coeficientes de Fourier da função , por meio da fórmula .
- Se , então . Em particular, como para a fixo temos como , segue-se que tende a zero, o que significa que os coeficientes de Fourier convergem para zero mais rápido que a k -ésima potência de n para qualquer .
Grupos compactos
Uma das propriedades interessantes da transformada de Fourier que mencionamos é que ela transporta convoluções para produtos pontuais. Se essa é a propriedade que procuramos preservar, pode-se produzir séries de Fourier em qualquer grupo compacto . Exemplos típicos incluem aqueles grupos clássicos que são compactos. Isso generaliza a transformada de Fourier para todos os espaços da forma L 2 ( G ), onde G é um grupo compacto, de forma que a transformada de Fourier carrega convoluções para produtos pontuais. A série de Fourier existe e converge de forma similar ao caso [− π , π ] .
Uma extensão alternativa para grupos compactos é o teorema de Peter-Weyl , que prova resultados sobre representações de grupos compactos análogos àqueles sobre grupos finitos.

Variedades Riemannianas
Se o domínio não for um grupo, não haverá convolução intrinsecamente definida. No entanto, se é uma variedade Riemanniana compacta , ela possui um operador de Laplace–Beltrami . O operador Laplace-Beltrami é o operador diferencial que corresponde ao operador Laplace para a variedade Riemanniana . Então, por analogia, pode-se considerar as equações de calor em . Como Fourier chegou à sua base tentando resolver a equação do calor, a generalização natural é usar as autosoluções do operador de Laplace-Beltrami como base. Isso generaliza a série de Fourier para espaços do tipo , onde é uma variedade Riemanniana. A série de Fourier converge de maneira semelhante ao caso. Um exemplo típico é tomar a esfera com a métrica usual, caso em que a base de Fourier consiste em harmônicos esféricos .
Grupos abelianos localmente compactos
A generalização para grupos compactos discutidos acima não se generaliza para grupos nonabelian não compactos . No entanto, há uma generalização direta para grupos Abelianos Localmente Compactos (LCA).
Isso generaliza a transformada de Fourier para ou , onde é um grupo LCA. Se for compacta, obtém-se também uma série de Fourier, que converge de forma semelhante ao caso, mas se for não compacta, obtém-se em vez disso uma integral de Fourier . Essa generalização produz a transformada de Fourier usual quando o grupo Abeliano localmente compacto subjacente é .
Extensões
Série de Fourier em um quadrado
Também podemos definir a série de Fourier para funções de duas variáveis e no quadrado :
Além de ser útil para resolver equações diferenciais parciais, como a equação do calor, uma aplicação notável da série de Fourier no quadrado é na compressão de imagens . Em particular, o padrão de compressão de imagem JPEG usa a transformada de cosseno discreta bidimensional , uma forma discreta da transformada de cosseno de Fourier , que usa apenas o cosseno como a função de base.
Para matrizes bidimensionais com aparência escalonada, metade dos coeficientes da série de Fourier desaparece devido à simetria adicional.
Série de Fourier da função periódica da rede de Bravais
Uma rede de Bravais tridimensional é definida como o conjunto de vetores da forma:
Assim, podemos definir uma nova função,
Esta nova função, , é agora uma função de três variáveis, cada uma das quais tem periodicidade , , e respectivamente:
Isso nos permite construir um conjunto de coeficientes de Fourier, cada um sendo indexado por três inteiros independentes . A seguir, usamos notação de função para denotar esses coeficientes, onde anteriormente usamos subscritos. Se escrevermos uma série for no intervalo de , podemos definir o seguinte:
E então podemos escrever:
Definindo ainda:
Podemos escrever novamente como:
Finalmente aplicando o mesmo para a terceira coordenada, definimos:
Escrevemos como:
Reorganizando:
Agora, todo vetor de rede recíproca pode ser escrito (mas não significa que seja a única maneira de escrever) como , onde são inteiros e são vetores de rede recíproca a serem satisfeitos ( para , e para ). Então, para qualquer vetor de rede recíproca arbitrária e vetor de posição arbitrária no espaço da rede de Bravais original, seu produto escalar é:
Portanto, é claro que em nossa expansão de , a soma é, na verdade, sobre vetores de rede recíproca:
onde
assumindo
(pode ser vantajoso, para simplificar os cálculos, trabalhar em um sistema de coordenadas retangular, no qual acontece que é paralelo ao eixo
x , encontra-se no plano xy e possui componentes de todos os três eixos) . O denominador é exatamente o volume da célula unitária primitiva que é delimitada pelos três vetores primitivos , e . Em particular, agora sabemos quePodemos escrever agora como uma integral com o sistema de coordenadas tradicional sobre o volume da célula primitiva, em vez de com as variáveis , e :
Interpretação do espaço de Hilbert
Na linguagem dos espaços de Hilbert , o conjunto de funções é uma
base ortonormal para o espaço de funções quadráticas integráveis em . Este espaço é na verdade um espaço de Hilbert com um produto interno dado para quaisquer dois elementos e por:- onde é o complexo conjugado de
O resultado básico da série de Fourier para espaços de Hilbert pode ser escrito como

Isso corresponde exatamente à formulação exponencial complexa dada acima. A versão com senos e cossenos também é justificada com a interpretação do espaço de Hilbert. De fato, os senos e cossenos formam um conjunto ortogonal :
Teorema de Fourier provando a convergência da série de Fourier
Esses teoremas, e variações informais deles que não especificam as condições de convergência, às vezes são chamados genericamente de teorema de Fourier ou teorema de Fourier .
A Eq.7 anterior
Propriedade dos mínimos quadrados
O teorema de Parseval implica que:
Teorema — O polinômio trigonométrico é o único melhor polinômio trigonométrico de grau aproximado , no sentido de que, para qualquer polinômio trigonométrico de grau , temos:
teoremas de convergência
Devido à propriedade dos mínimos quadrados e devido à completude da base de Fourier, obtemos um resultado de convergência elementar.
Teorema — Se pertence a (um intervalo de comprimento ), então converge para em , ou seja, converge para 0 como .
Já mencionamos que se é continuamente diferenciável, então é o coeficiente de Fourier da derivada . Segue-se, essencialmente da
desigualdade de Cauchy-Schwarz , que é absolutamente somável. A soma desta série é uma função contínua, igual a , pois a série de Fourier converge na média para :Teorema — Se , então converge para uniformemente (e, portanto, também pontualmente ).
Este resultado pode ser provado facilmente se ainda for assumido como sendo , pois nesse caso tende a zero como . Mais geralmente, a série de Fourier é absolutamente somável, portanto converge uniformemente para , desde que satisfaça uma condição de ordem de
Hölder . No caso absolutamente somável, a desigualdade:prova a convergência uniforme.
Muitos outros resultados sobre a convergência da série de Fourier são conhecidos, variando desde o resultado moderadamente simples de que a série converge em se é diferenciável em , até o resultado muito mais sofisticado de
Lennart Carleson de que a série de Fourier de uma função realmente converge em quase todos os lugares .Divergência
Como as séries de Fourier têm propriedades de convergência tão boas, muitos ficam surpresos com alguns dos resultados negativos. Por exemplo, a série de Fourier de uma função periódica T contínua não precisa convergir pontualmente. O princípio da limitação uniforme fornece uma prova não construtiva simples desse fato.
Em 1922, Andrey Kolmogorov publicou um artigo intitulado Une série de Fourier-Lebesgue divergente presque partout, no qual deu um exemplo de uma função integrável de Lebesgue cuja série de Fourier diverge em quase todos os lugares. Mais tarde, ele construiu um exemplo de uma função integrável cuja série de Fourier diverge em todos os lugares ( Katznelson 1976 ).
Veja também
- teorema ATS
- Dirichlet Kernel
- Transformada discreta de Fourier
- Transformação rápida de Fourier
- teorema de Fejér
- análise de Fourier
- Série de senos e cossenos de Fourier
- transformada de Fourier
- fenômeno de Gibbs
- Série Fourier de meia gama
- Série de Laurent – a substituição q = e ix transforma uma série de Fourier em uma série de Laurent, ou vice-versa. Isso é usado na expansão da série q do invariante j .
- Análise espectral de mínimos quadrados
- transformação multidimensional
- teoria espectral
- Teoria de Sturm-Liouville
- Integrais do teorema residual de f ( z ), singularidades, pólos
Notas
Referências
Leitura adicional
- William E. Boyce; Richard C. DiPrima (2005). Equações diferenciais elementares e problemas de valor de contorno (8ª ed.). Nova Jersey: John Wiley & Sons, Inc. ISBN 0-471-43338-1.
- Joseph Fourier, traduzido por Alexander Freeman (2003). A Teoria Analítica do Calor . Publicações de Dover. ISBN 0-486-49531-0.2003 republicação integral da tradução inglesa de 1878 por Alexander Freeman da obra de Fourier Théorie Analytique de la Chaleur , publicada originalmente em 1822.
- Enrique A. González-Velasco (1992). "Conexões em Análise Matemática: O Caso da Série de Fourier". Mensal Matemático Americano . 99 (5): 427–441. doi : 10.2307/2325087 . JSTOR 2325087 .
- Fetter, Alexander L.; Walecka, John Dirk (2003). Mecânica Teórica de Partículas e Contínuos . Correio. ISBN 978-0-486-43261-8.
- Felix Klein , Desenvolvimento da matemática no século XIX . Mathsci Press Brookline, Mass, 1979. Traduzido por M. Ackerman de Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert , Springer, Berlin, 1928.
- Walter Rudin (1976). Princípios de análise matemática (3ª ed.). Nova York: McGraw-Hill, Inc. ISBN 0-07-054235-X.
- A. Zygmund (2002). Série trigonométrica (terceira ed.). Cambridge: Cambridge University Press. ISBN 0-521-89053-5.A primeira edição foi publicada em 1935.
links externos
- "Fourier series" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
- Hobson, Ernest (1911). . Encyclopædia Britannica . Vol. 10 (11ª ed.). pp. 753–758.
- Weisstein, Eric W. "Fourier Series" . MathWorld .
- Joseph Fourier - Um site sobre a vida de Fourier que foi usado para a seção histórica deste artigo no Wayback Machine (arquivado em 5 de dezembro de 2001)
Este artigo incorpora material de exemplo da série Fourier no PlanetMath , que é licenciado sob a licença Creative Commons Attribution/Share-Alike .


























![(-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)



![{\displaystyle {\begin{aligned}A_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x)\cos(nx)\, dx=0,\quad n\geq 0.\\[4pt]B_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }s(x) \sin(nx)\,dx\\[4pt]&=-{\frac {2}{\pi n}}\cos(n\pi )+{\frac {2}{\pi ^{2}n ^{2}}}\sin(n\pi )\\[4pt]&={\frac {2\,(-1)^{n+1}}{\pi n}},\quad n\geq 1.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60820ad01df637675beb2c56a9db388cd0539490)

![{\displaystyle {\begin{aligned}s(x)&=A_{0}+\sum _{n=1}^{\infty }A_{n}\cos \left(nx\right)+B_{n }\sin \left(nx\right)\\[4pt]&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^ {n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbb {Z} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cb0668def0fb376e8a1d8541263b10508260a77)
















![{\displaystyle [x_{0},x_{0}+P],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74358f52e616039efc9b1fcc9568f99f6ae93463)
![{\displaystyle \mathrm {X} _{f}(\tau )={\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left(2\pi f(x -\tau )\direita)\,dx;\quad \tau \in \left[0,{\tfrac {2\pi }{f}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2868da53c5e3ed8528137f2aaf139400251e74e)













![{\displaystyle {\begin{aligned}\mathrm {X} _{n}(\varphi )&={\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left (2\pi {\tfrac {n}{P}}x-\varphi \direita)\,dx;\quad \varphi \in [0,2\pi ]\\&=\cos(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \cos \left(2\pi {\tfrac {n}{P}}x\right)\,dx } _{A_{n}}+\sin(\varphi )\cdot \underbrace {{\tfrac {2}{P}}\int _{P}s(x)\cdot \sin \left(2\pi {\tfrac {n}{P}}x\direita)\,dx} _{B_{n}}\\&=\cos(\varphi )\cdot A_{n}+\sin(\varphi )\cdot B_{n}\end{alinhado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b72e0b83fd20619ddc5f938cf5280cfd3443820)








![{\displaystyle [x_{0},x_{0}+P]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ef79a1b836ec65eacb0d2c73464996d2b7830ba)






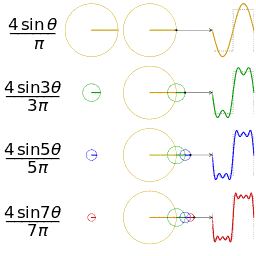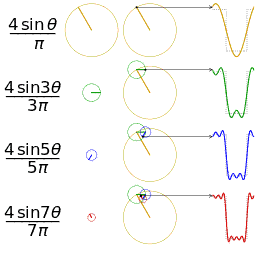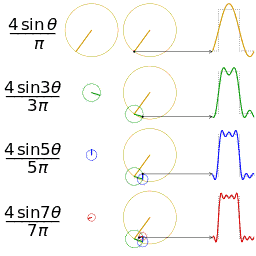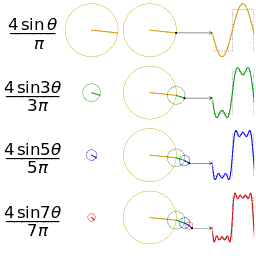


![{\displaystyle {\hat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4759449679108f08a78be5a080c3db89dc27ffea)
![{\displaystyle S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4222b53917b43f530116997b71049100c95586)
![{\displaystyle {\begin{aligned}s(x)&=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{2\pi inx/ P}&&{\text{notação matemática comum}}\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P} &&{\text{notação de engenharia comum}}\end{alinhado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8427f6c9d293e4fd06f52432445973be52c41e)
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\ certo),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)


![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _ {n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\ ,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f -{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[ n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x).\end{alinhado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)










![{\displaystyle (x,y)\em [0,\pi ]\vezes [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c18734f151b17b5d3e325f79c7000826ab832610)



















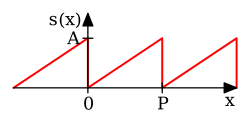








![{\displaystyle x\in [0,P].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06b058e43f16179590921d9669ac45cec21a975e)
![{\displaystyle S[n],R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/320b593144d771f4aac1aae12d9513debbd3b20f)


![{\displaystyle a\cdot S[n]+b\cdot R[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23622be4a50d54928d05c273e803240a2cb1e413)


![{\displaystyle S[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab628b28c49c04cab81d0bd30d19ee0797b0587c)

![{\displaystyle S^{*}[-n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3f6ea8a947b86f8a31046070359f6b8111a0bae)

![{\displaystyle S^{*}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3776c67c40997d8044720ef84de7575679cf9638)

![{\displaystyle {\frac {1}{2}}(S[n]+S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2eb44dffaae6c85870914249c054e33236b02cc8)

![{\displaystyle {\frac {1}{2i}}(S[n]-S^{*}[-n])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc039a9c12ae20a4b47337ae55bf8a7bc26d2e11)

![{\displaystyle \nome do operador {Re} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/140ebff319eb8eb7965d0ca86dcaadb21685177a)

![{\displaystyle \operatorname {Im} {(S[n])}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c726948120015ce0d482f5f7f4af81713342b5c)

![{\displaystyle S[n]\cdot e^{-i{\frac {2\pi x_{0}}{P}}n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fb7150e991a2642dc0c62cdee40602d99227420)


![{\displaystyle S[n-n_{0}]\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07385c0e5fd45d4e07a279a91668cf8894963e0c)



![{\textstyle \lim _{|n|\to \infty }S[n]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc04d857f6462ae29422edcada981c8a798d4b5)



![{\textstyle {\frac {1}{P}}\int _{P}|s(x)|^{2}\,dx=\sum _{n=-\infty }^{\infty }{\ Bigl |}S[n]{\Bigr |}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/263e69a5a58598591a5c06ca7e17ef8cfe92bdad)


![{\displaystyle S[n]\in \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5ef3e51d1a6c9fe833f0a436ad2906cfaa4d5a3)
![{\displaystyle {\frac {1}{P}}\int _{P}|s(x)|^{4}\,dx=\sum _{k=0}^{M-1}S[k ]\sum _{l=0}^{M-1}S^{*}[l]{\Bigg [}{\underset {k\geq l}{\sum _{m=kl}^{M- 1}}}S^{*}[m]S[m-(kl)]+{\underset {k<l}{\sum _{m=lk}^{M-1}}}S^{* }[m-(lk)]S[m]{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39c359b6c8df5068b8df3c592e303ee7be010e33)
![{\displaystyle S[n]\in \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b094e88b3fbb3d7754e0a9ea0138c296f4b0d137)
![{\displaystyle {\frac {1}{P}}\int _{P}|s(x)|^{4}\,dx=\sum _{k=0}^{M-1}S[k ]\soma _{l=0}^{M-1}S[l]\soma _{m=|kl|}^{M-1}S[m]S[m-|kl|]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9aa31cd2ec580a3b95affae1462abed113a86f12)



![{\displaystyle S[n]=c_{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4375307afdf29e78a31ef64b699dcb3e2fde140)


![{\displaystyle R[n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d8bbe147f3eb3fb318d09437a3540e054b0289)



![{\displaystyle H[n]=\{S*R\}[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5d3978629d1c2cd954f884509a1bb360f01cac5)

![{\displaystyle H[n]=P\cdot S[n]\cdot R[n].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1804f502413d4e3e5f28f8715c52e2a3d7e7e9a6)


![{\displaystyle L^{1}([0,2\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd16426bda528c05e32e97bfba7f51b598c081b8)





![{\displaystyle {\widehat {s'}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a50845d25c79fe9547d0194fce67a390efc1a4ed)

![{\displaystyle {\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efb5adbeb52d198894dc8f70ec8c434f0e193e6b)
![{\displaystyle {\widehat {s'}}[n]=em{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d281471757291b705a757faa55af0f1cebf8a0b6)

![{\displaystyle {\widehat {s^{(k)}}}[n]=(in)^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b0120eafbcb1c02b4c2f81f5589fdc328c28bd20)

![{\displaystyle {\widehat {s^{(k)}}}[n]\para 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ddeff4d322091a8ec85a30a10d584d426d703b1)

![{\displaystyle |n|^{k}{\widehat {s}}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/541244c281f9472e99fca9b32f2cd7676434d09c)


![[-\pi,\pi]](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb064fd6c55820cfa660eabeeda0f6e3c4935ae6)




![{\displaystyle [-\pi ,\pi ]\vezes [-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df436805f50de7386abdb2a9d058672ec1b4cebb)
![{\displaystyle {\begin{aligned}f(x,y)&=\sum _{j,k\in \mathbb {Z} }c_{j,k}e^{ijx}e^{iky},\ \[5pt]c_{j,k}&={\frac {1}{4\pi ^{2}}}\int _{-\pi }^{\pi }\int _{-\pi }^ {\pi }f(x,y)e^{-ijx}e^{-iky}\,dx\,dy.\end{alinhados}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec3723d7051701ab4530dce39f1480cef835981)



















![{\displaystyle \left[0,a_{1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/187cf2c27876a96c668f73266f673002808773ac)



![{\displaystyle {\begin{aligned}h^{\mathrm {dois} }(m_{1},m_{2},x_{3})&\triangleq {\frac {1}{a_{2}}} \int _{0}^{a_{2}}h^{\mathrm {one} }(m_{1},x_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0} ^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{ 2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}} {a_{2}}}x_{2}\direita)}\end{alinhado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/342f2441863562e2188c632ea98d105ddb4ce5f1)

![{\displaystyle {\begin{aligned}h^{\mathrm {três} }(m_{1},m_{2},m_{3})&\triangleq {\frac {1}{a_{3}}} \int _{0}^{a_{3}}h^{\mathrm {dois} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0} ^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{ 1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left( {\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}+{\frac {m_{3} }{a_{3}}}x_{3}\direita)}\end{alinhado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8c3fac5e04d1272c87fd58d3217a691214d09b)



















![{\displaystyle {\begin{vmatrix}{\dfrac {\parcial x_{1}}{\parcial x}}&{\dfrac {\parcial x_{1}}{\parcial y}}&{\dfrac {\ parcial x_{1}}{\parcial z}}\\[12pt]{\dfrac {\parcial x_{2}}{\parcial x}}&{\dfrac {\parcial x_{2}}{\parcial y }}&{\dfrac {\parcial x_{2}}{\parcial z}}\\[12pt]{\dfrac {\parcial x_{3}}{\parcial x}}&{\dfrac {\parcial x_ {3}}{\partial y}}&{\dfrac {\parcial x_{3}}{\parcial z}}\end{vmatriz}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5df9134486606d6a55c8ec4a96ee3ca353e924)












![{\displaystyle L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f84fea7a212acaf14649b6cdcca282b0646a8b0)












![{\displaystyle s_{_{N}}(x)=\sum _{n=-N}^{N}S[n]\ e^{i{\tfrac {2\pi }{P}}nx} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b030eaf773387de3787b4a003ef7599624be959)
![{\displaystyle p_{_{N}}(x)=\sum _{n=-N}^{N}p[n]\ e^{i{\tfrac {2\pi }{P}}nx} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a29c02020f3c186b790b680deabe8e985ebcd700)







![{\displaystyle (i\cdot n)S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a89ae55b94c8d25d1f3927c5ba4eb65ac7c4762)

![{\displaystyle n^{2}S[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/340e0b24995005f3669a865a57edb4035b77ca2d)


![{\displaystyle \sup _{x}|s(x)-s_{_{N}}(x)|\leq \sum _{|n|>N}|S[n]|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8225d322a5b676b2b1709c2a636dcd092ff11ec)
