Campo (matemática) - Field (mathematics)

Estruturas algébricas
grupo -como Grupo Semigrupo  / Monóide Rack e quandle Quasigroup e loop Grupo abeliano Magma Grupo de mentiras Teoria do grupo
Semelhante a um anel Anel Rng Semiring Quase-anel Anel comutativo Domínio integral Campo Anel de divisão Teoria do anel
Semelhante a uma treliça Malha Semilattice Malha complementada Ordem total Álgebra Heyting álgebra booleana Mapa de treliças Teoria da Malha
Módulo- like Módulo Grupo com operadoras Espaço vetorial Álgebra Linear
álgebra -como Álgebra Associativo Não associativo Álgebra de composição Álgebra de mentira Classificado Bialgebra
v t e

Estrutura algébrica → Teoria dos anéis Teoria dos anéis
Conceitos Básicos argolas • Subrings • Ideal • Anel de quociente • Ideal fracionário • Anel quociente total • Anel de produto • Produto gratuito de álgebras associativas • Produto tensor de anéis Homomorfismos de anel • Kernel • Automorfismo interno • Endomorfismo de Frobenius Estruturas algébricas • Módulo • Álgebra associativa • Anel graduado • Anel involutivo • Categoria de anéis • Toque inicial ${\ displaystyle \ mathbb {Z}}$ • Anel terminal ${\ displaystyle 0 = \ mathbb {Z} _ {1}}$ Estruturas relacionadas • Campo • Campo finito • Anel não associativo • Anel de mentira • anel Jordan • Semiring • Semifield
Álgebra comutativa Anéis comutativos • Domínio integral • Domínio totalmente fechado • Domínio GCD • Domínio de fatoração único • Domínio ideal principal • Domínio euclidiano • Campo • Campo finito • Anel de composição • Anel polinomial • Anel série de potência formal Teoria dos números algébricos • Campo de número algébrico • Anel de inteiros • Independência algébrica • Teoria dos números transcendentais • Grau de transcendência Teoria dos números p -adic e decimais • Limite direto / limite inverso • Anel zero ${\ displaystyle \ mathbb {Z} _ {1}}$ • Módulo de inteiros p n ${\ displaystyle \ mathbb {Z} / p ^ {n} \ mathbb {Z}}$ • Prüfer p -ring ${\ displaystyle \ mathbb {Z} (p ^ {\ infty})}$ • Base - anel circular p ${\ displaystyle \ mathbb {T}}$ • Base - p inteiros ${\ displaystyle \ mathbb {Z}}$ • racionais p -adic ${\ displaystyle \ mathbb {Z} [1 / p]}$ • Base - p números reais ${\ displaystyle \ mathbb {R}}$ • inteiros p -adic ${\ displaystyle \ mathbb {Z} _ {p}}$ • números p -adic ${\ displaystyle \ mathbb {Q} _ {p}}$ • solenóide p -adic ${\ displaystyle \ mathbb {T} _ {p}}$ Geometria algébrica • Variedade afim
Álgebra não comutativa Anéis não comutativos • Anel de divisão • Anel semiprimitivo • Anel simples • Comutador Geometria algébrica não comutativa Álgebra grátis Álgebra de Clifford • Álgebra geométrica Álgebra do operador
v t e

Em matemática , um campo é um conjunto no qual adição , subtração , multiplicação e divisão são definidas e se comportam como as operações correspondentes em números racionais e reais . Um campo é, portanto, uma estrutura algébrica fundamental amplamente usada em álgebra , teoria dos números e muitas outras áreas da matemática.

Os campos mais conhecidos são o campo dos números racionais , o campo dos números reais e o campo dos números complexos . Muitos outros campos, tais como campos de funções racionais , campos de função algébricas , campos de números algébricos e p campos -adic são comumente utilizado e estudado na matemática, particularmente na teoria dos números e geometria algébrica . A maioria dos protocolos criptográficos dependem de campos finitos , ou seja, campos com muitos elementos finitos .

A relação de dois campos é expressa pela noção de uma extensão de campo . A teoria de Galois , iniciada por Évariste Galois na década de 1830, dedica-se a compreender as simetrias das extensões de campo. Entre outros resultados, essa teoria mostra que a trissecção do ângulo e a quadratura do círculo não podem ser feitas com compasso e régua . Além disso, mostra que as equações quínticas são, em geral, sem solução algébrica.

Os campos servem como noções fundamentais em vários domínios matemáticos. Isso inclui diferentes ramos da análise matemática , que se baseiam em campos com estrutura adicional. Teoremas básicos em análise dependem das propriedades estruturais do campo dos números reais. Mais importante ainda, para fins algébricos, qualquer campo pode ser usado como escalar para um espaço vetorial , que é o contexto geral padrão para álgebra linear . Os campos numéricos , irmãos do campo dos números racionais, são estudados em profundidade na teoria dos números . Os campos de função podem ajudar a descrever propriedades de objetos geométricos.

Definição

Informalmente, um campo é um conjunto, junto com duas operações definidas nesse conjunto: uma operação de adição escrita como a + b , e uma operação de multiplicação escrita como a ⋅ b , ambas as quais se comportam da mesma forma como se comportam para números racionais e reais , incluindo a existência de um inverso aditivo - a para todos os elementos a , e de um inverso multiplicativo b ^-1 para cada elemento diferente de zero b . Isso permite também considerar as chamadas operações inversas de subtração , a - b , e divisão , a / b , definindo:

a - b = a + (- b ) ,

a / b = a ⋅ b ⁻¹ .

Definição clássica

Formalmente, um campo é um conjunto F junto com duas operações binárias em F chamadas adição e multiplicação . Uma operação de binário em F é um mapeamento F × F → F , isto é, uma correspondência que se associa com cada par ordenado de elementos de F um elemento unicamente determinada de F . O resultado da adição de um e b é chamada a soma de um e b , e é denotado um + b . Da mesma forma, o resultado da multiplicação de um e b é chamado o produto de um e b , e é denotado ab ou um ⋅ b . Essas operações são necessárias para satisfazer as seguintes propriedades, conhecidas como axiomas de campo (nesses axiomas, a , b e c são elementos arbitrários do campo F ):

• Associatividade de adição e multiplicação: a + ( b + c ) = ( a + b ) + c , e a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c .
• Comutatividade de adição e multiplicação: a + b = b + a , e a ⋅ b = b ⋅ a .
• Aditivo e identidade multiplicativo : existem dois elementos diferentes 0 e 1 em F de tal modo que um + 0 = um e um ⋅ 1 = um .
• Aditivos inversos : para cada a em F , existe um elemento em F , denotado - a , denominado inverso aditivo de a , tal que a + (- a ) = 0 .
• Inversos multiplicativos : para cada a ≠ 0 em F , existe um elemento em F , denotado por a ⁻¹ ou 1 / a , denominado inverso multiplicativo de a , tal que a ⋅ a ⁻¹ = 1 .
• Distributividade da multiplicação sobre a adição: a ⋅ ( b + c ) = ( a ⋅ b ) + ( a ⋅ c ) .

Isso pode ser resumido dizendo: um campo tem duas operações, chamadas adição e multiplicação; é um grupo abeliano sob adição com 0 como a identidade aditiva; os elementos diferentes de zero são um grupo abeliano sob multiplicação com 1 como a identidade multiplicativa; e a multiplicação distribui sobre a adição.

Ainda mais resumido: um campo é um anel comutativo onde e todos os elementos diferentes de zero são invertíveis. ${\ displaystyle 0 \ neq 1}$

Definição alternativa

Os campos também podem ser definidos de maneiras diferentes, mas equivalentes. Pode-se definir alternativamente um campo por quatro operações binárias (adição, subtração, multiplicação e divisão) e suas propriedades necessárias. A divisão por zero é, por definição, excluída. Para evitar quantificadores existenciais , os campos podem ser definidos por duas operações binárias (adição e multiplicação), duas operações unárias (produzindo os inversos aditivos e multiplicativos, respectivamente) e duas operações nulas (as constantes 0 e 1 ). Essas operações estão então sujeitas às condições acima. Evitar quantificadores existenciais é importante em matemática e computação construtiva . Pode-se definir equivalentemente um campo pelas mesmas duas operações binárias, uma operação unária (o inverso multiplicativo) e duas constantes 1 e −1 , uma vez que 0 = 1 + (−1) e - a = (−1) a .

Exemplos

Números racionais

Os números racionais foram amplamente utilizados muito antes da elaboração do conceito de campo. Eles são números que podem ser escritos como frações a / b , onde a e b são inteiros e b ≠ 0 . O inverso aditivo de tal fração é - a / b , e o inverso multiplicativo (desde que a ≠ 0 ) seja b / a , que pode ser visto da seguinte forma:

${\ displaystyle {\ frac {b} {a}} \ cdot {\ frac {a} {b}} = {\ frac {ba} {ab}} = 1.}$

Os axiomas de campo requeridos abstratamente reduzem-se a propriedades padrão de números racionais. Por exemplo, a lei da distributividade pode ser provada da seguinte forma:

${\ displaystyle {\ begin {alinhado} & {\ frac {a} {b}} \ cdot \ left ({\ frac {c} {d}} + {\ frac {e} {f}} \ right) \ \ [6pt] = {} & {\ frac {a} {b}} \ cdot \ left ({\ frac {c} {d}} \ cdot {\ frac {f} {f}} + {\ frac { e} {f}} \ cdot {\ frac {d} {d}} \ right) \\ [6pt] = {} & {\ frac {a} {b}} \ cdot \ left ({\ frac {cf } {df}} + {\ frac {ed} {fd}} \ right) = {\ frac {a} {b}} \ cdot {\ frac {cf + ed} {df}} \\ [6pt] = {} & {\ frac {a (cf + ed)} {bdf}} = {\ frac {acf} {bdf}} + {\ frac {aed} {bdf}} = {\ frac {ac} {bd} } + {\ frac {ae} {bf}} \\ [6pt] = {} & {\ frac {a} {b}} \ cdot {\ frac {c} {d}} + {\ frac {a} {b}} \ cdot {\ frac {e} {f}}. \ end {alinhado}}}$

Números reais e complexos

Os números reais R , com as operações usuais de adição e multiplicação, também formam um campo. Os números complexos C consistem em expressões

a + bi , com a , b real,

onde i é a unidade imaginária , ou seja, um número (não real) que satisfaz i ² = −1 . Adição e multiplicação de números reais são definidos de tal forma que as expressões deste tipo satisfazer todos os axiomas de campo e, assim, manter por C . Por exemplo, a lei distributiva impõe

( a + bi ) ( c + di ) = ac + bci + adi + bdi ² = ac - bd + ( bc + ad ) i .

É imediato que esta é novamente uma expressão do tipo acima e, portanto, os números complexos formam um campo. Os números complexos podem ser representados geometricamente como pontos no plano , com as coordenadas cartesianas dadas pelos números reais de sua expressão descritiva, ou como as setas da origem até esses pontos, especificadas por seu comprimento e um ângulo fechado em alguma direção distinta. A adição corresponde então a combinar as setas ao paralelogramo intuitivo (adicionando as coordenadas cartesianas), e a multiplicação é - menos intuitivamente - combinando a rotação e a escala das setas (adicionando os ângulos e multiplicando os comprimentos). Os campos de números reais e complexos são usados ​​em matemática, física, engenharia, estatística e muitas outras disciplinas científicas.

Números construtíveis

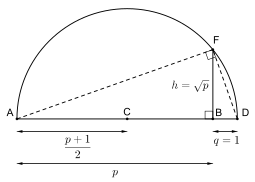
Na antiguidade, vários problemas geométricos diziam respeito à (in) viabilidade de construir certos números com compasso e régua . Por exemplo, os gregos desconheciam que, em geral, é impossível trissecionar um determinado ângulo dessa maneira. Esses problemas podem ser resolvidos usando o campo de números construtíveis . Os números reais construtíveis são, por definição, comprimentos de segmentos de linha que podem ser construídos a partir dos pontos 0 e 1 em um número finito de passos usando apenas compasso e régua . Esses números, dotados das operações de campo dos números reais, restritos aos números construtíveis, formam um campo, que inclui propriamente o campo Q dos números racionais. A ilustração mostra a construção de raízes quadradas de números constructible, não necessariamente, contidos Q . Usando a etiqueta na ilustração, construa os segmentos AB , BD e um semicírculo sobre AD (centro no ponto médio C ), que cruza a linha perpendicular através de B em um ponto F , a uma distância exata de B quando BD tem comprimento 1. ${\ displaystyle h = {\ sqrt {p}}}$

Nem todos os números reais são construtíveis. Pode-se mostrar que não é um número construtível, o que implica que é impossível construir com compasso e retidão o comprimento da lateral de um cubo com volume 2 , outro problema colocado pelos antigos gregos. ${\ displaystyle {\ sqrt [{3}] {2}}}$

Um campo com quatro elementos

Adição	Multiplicação
+ O eu UMA B O O eu UMA B eu eu O B UMA UMA UMA B O eu B B UMA eu O	⋅ O eu UMA B O O O O O eu O eu UMA B UMA O UMA B eu B O B eu UMA

Além de sistemas numéricos familiares, como os racionais, existem outros exemplos menos imediatos de campos. O exemplo seguinte é um campo constituído por quatro elementos chamados ó , I , A , e B . A notação é escolhida de forma que O desempenhe o papel do elemento de identidade aditivo (denotado como 0 nos axiomas acima) e I é a identidade multiplicativa (denotado como 1 nos axiomas acima). Os axiomas de campo podem ser verificados usando um pouco mais de teoria de campo ou por computação direta. Por exemplo,

A ⋅ ( B + A ) = A ⋅ I = A , que é igual a A ⋅ B + A ⋅ A = I + B = A , conforme exigido pela distributividade.

Esse campo é chamado de corpo finito com quatro elementos e é denotado por F ₄ ou GF (4) . O subconjunto formado por O e I (destacado em vermelho nas tabelas à direita) também é um campo, conhecido como campo binário F ₂ ou GF (2) . No contexto da ciência da computação e da álgebra booleana , O e I são freqüentemente denotados respectivamente por falso e verdadeiro , a adição é então denotada XOR (ou exclusivo), e a multiplicação é denotada por AND . Em outras palavras, a estrutura do campo binário é a estrutura básica que permite a computação com bits .

Noções elementares

Nesta secção, F indica um campo arbitrário e um e b são arbitrárias elementos de F .

Consequências da definição

Um tem a ⋅ 0 = 0 e - a = (−1) ⋅ a . Em particular, pode-se deduzir o inverso aditivo de cada elemento assim que souber -1 .

Se ab = 0 então a ou b deve ser 0, pois, se a ≠ 0 , então b = ( a ⁻¹ a ) b = a ⁻¹ ( ab ) = a ⁻¹ ⋅ 0 = 0 . Isso significa que todo campo é um domínio integral .

Além disso, as seguintes propriedades são verdadeiras para quaisquer elementos a e b :

-0 = 0

1 ⁻¹ = 1

(- (- a )) = a

(- a ) ⋅ b = a ⋅ (- b ) = - ( a ⋅ b )

( a ⁻¹ ) ⁻¹ = a se a ≠ 0

O grupo aditivo e multiplicativo de um campo

Os axiomas de um campo F implicam que ele é um grupo abeliano por adição. Esse grupo é chamado de grupo aditivo do campo e às vezes é denotado por ( F , +) quando denotá-lo simplesmente como F pode ser confuso.

Da mesma forma, os elementos diferentes de zero de F formam um grupo abeliano sob multiplicação, chamado de grupo multiplicativo , e denotado por ( F \ {0}, ⋅) ou apenas F \ {0} ou F ^* .

Um campo pode, assim, ser definido como o conjunto F equipado com duas operações denotadas como uma adição e uma multiplicação de modo que F é um grupo abeliano sob adição, F \ {0} é um grupo abeliano sob multiplicação (onde 0 é o elemento de identidade do adição), e a multiplicação é distributiva em relação à adição. Algumas afirmações elementares sobre campos podem, portanto, ser obtidas aplicando-se fatos gerais de grupos . Por exemplo, os inversos aditivos e multiplicativos - a e a ⁻¹ são determinados exclusivamente por a .

O requisito 1 ≠ 0 segue, porque 1 é o elemento identidade de um grupo que não contém 0. Assim, o anel trivial , consistindo de um único elemento, não é um campo.

Cada subgrupo finito do grupo multiplicativo de um campo é cíclico (ver Raiz da unidade § Grupos cíclicos ).

Característica

Além da multiplicação de dois elementos de F , é possível definir o produto n ⋅ a de um elemento arbitrário a de F por um número inteiro positivo n como sendo a soma de n

a + a + ⋯ + a (que é um elemento de F. )

Se não houver um número inteiro positivo tal que

n ⋅ 1 = 0 ,

então F diz-se que tem a característica 0. Por exemplo, o campo de números racionais Q tem a característica 0, uma vez que nenhum inteiro positivo n é zero. Caso contrário, se não é um número inteiro positivo n satisfazer esta equação, o menor número inteiro positivo, tal pode ser demonstrado ser um número primo . Geralmente é denotado por pe, então, diz -se que o campo tem a característica p . Por exemplo, o campo F ₄ tem característica desde 2 (na notação da tabela adição acima) I + I = O .

Se F tem característica p , em seguida, p ⋅ um = 0 para todos os um em F . Isso implica que

( a + b ) ^p = a ^p + b ^p ,

uma vez que todos os outros coeficientes binomiais que aparecem na fórmula binomial são divisíveis por p . Aqui, a ^p  : = a ⋅ a ⋅ ⋯ ⋅ a ( p fatores) é a p -ésima potência, ou seja, o p- produto do elemento a . Portanto, o mapa de Frobenius

Fr: F → F , x ⟼ x ^p

é compatível com a adição em F (e também com a multiplicação) e é, portanto, um homomorfismo de campo. A existência desse homomorfismo torna os campos da característica p bastante diferentes dos campos da característica 0.

Subcampos e campos principais

Um subcampo E de um campo F é um subconjunto de M que é um campo com respeito às operações de campo de F . Equivalentemente, E é um subconjunto de F que contém 1 e é fechado sob adição, multiplicação, inverso aditivo e inverso multiplicativo de um elemento diferente de zero. Isto significa que um ε E , que para todos um , b ε E tanto um + b e um ⋅ b são em E , e de que para todo um ≠ 0 em E , tanto - um e 1 / um estão em E .

Os homomorfismos de campo são mapas f : E → F entre dois campos tais que f ( e ₁ + e ₂ ) = f ( e ₁ ) + f ( e ₂ ) , f ( e ₁ e ₂ ) = f ( e ₁ ) f ( e ₂ ) , e f (1 _e ) = 1 _F , onde a e ₁ e e ₂ são elementos arbitrários de e . Todos os homomorfismos de campo são injetivos . Se f também for sobrejetivo , é chamado de isomorfismo (ou os campos E e F são chamados de isomórficos).

Um campo é chamado de campo primo se não tiver subcampos adequados (ou seja, estritamente menores). Qualquer campo F contém um campo primo. Se a característica de F for p (um número primo), o corpo primo é isomorfo ao corpo finito F _p apresentado abaixo. Caso contrário, o campo principal é isomorfo a Q .

Campos finitos

Os campos finitos (também chamados de campos de Galois ) são campos com muitos elementos finitos, cujo número também é conhecido como a ordem do campo. O exemplo introdutório acima F ₄ é um campo com quatro elementos. Seu subcampo F ₂ é o menor campo, porque por definição um campo tem pelo menos dois elementos distintos 1 ≠ 0 .

Os campos finitos mais simples, com ordem primária, são mais diretamente acessíveis usando aritmética modular . Para um número inteiro positivo fixo n , "módulo n " aritmético significa trabalhar com os números

Z / n Z = {0, 1, ..., n - 1}.

A adição e multiplicação neste conjunto são feitas realizando a operação em questão no conjunto Z de inteiros, dividindo por n e tomando o resto como resultado. Essa construção produz um campo precisamente se n for um número primo . Por exemplo, tomar o primo n = 2 resulta no campo F ₂ mencionado acima . Para n = 4 e mais geralmente, para qualquer número composto (ou seja, qualquer número n que pode ser expresso como um produto n = r ⋅ s de dois números naturais estritamente menores), Z / n Z não é um campo: o produto de dois elementos diferentes de zero são zero, pois r ⋅ s = 0 em Z / n Z , o que, como foi explicado acima , impede que Z / n Z seja um campo. O campo Z / p Z com p elementos ( p sendo primo) construído dessa maneira é geralmente denotado por F _p .

Todo corpo finito F tem q = p ⁿ elementos, onde p é primo en ≥ 1 . Esta afirmação é válida porque F pode ser visto como um espaço vetorial sobre seu campo primo. A dimensão desse espaço vetorial é necessariamente finita, digamos n , o que implica a afirmação afirmada.

Um campo com q = p ⁿ elementos pode ser construído como o campo de divisão do polinômio

f ( x ) = x ^q - x .

Esse campo de divisão é uma extensão de F _p em que o polinômio f tem q zeros. Isso significa que f tem tantos zeros quanto possível, pois o grau de f é q . Para q = 2 ² = 4 , pode ser verificado caso a caso usando a tabuada de multiplicação acima que todos os quatro elementos de F ₄ satisfazem a equação x ⁴ = x , então eles são zeros de f . Em contraste, em F ₂ , f tem apenas dois zeros (ou seja, 0 e 1), portanto, f não se divide em fatores lineares neste campo menor. Elaborando ainda mais as noções básicas da teoria dos campos, pode-se mostrar que dois campos finitos com a mesma ordem são isomórficos. Assim, é habitual para falar do campo finito com q elementos, indicados por F _q ou GF ( q ) .

História

Historicamente, três disciplinas algébricas levaram ao conceito de um campo: a questão da resolução de equações polinomiais, teoria dos números algébricos e geometria algébrica . Um primeiro passo em direção à noção de um campo foi dado em 1770 por Joseph-Louis Lagrange , que observou que permutando os zeros x ₁ , x ₂ , x ₃ de um polinômio cúbico na expressão

( x ₁ + ωx ₂ + ω ² x ₃ ) ³

(com ω sendo uma terceira raiz da unidade ) produz apenas dois valores. Dessa forma, Lagrange explicou conceitualmente o método clássico de solução de Scipione del Ferro e François Viète , que procede reduzindo uma equação cúbica de um x desconhecido a uma equação quadrática de x ³ . Junto com uma observação semelhante para equações de grau 4 , Lagrange vinculou o que acabou se tornando o conceito de campos e o conceito de grupos. Vandermonde , também em 1770, e mais amplamente, Carl Friedrich Gauss , em seu Disquisitiones Arithmeticae (1801), estudou a equação

x ^p = 1

para um p primo e, novamente usando linguagem moderna, o grupo de Galois cíclico resultante . Gauss deduziu que um p -gon regular pode ser construído se p = 2 ^{2 k} + 1 . Com base no trabalho de Lagrange, Paolo Ruffini afirmou (1799) que as equações quínticas (equações polinomiais de grau 5) não podem ser resolvidas algebricamente; no entanto, seus argumentos eram falhos. Essas lacunas foram preenchidas por Niels Henrik Abel em 1824. Évariste Galois , em 1832, concebeu critérios necessários e suficientes para que uma equação polinomial fosse algebricamente solucionável, estabelecendo assim o que hoje é conhecido como teoria de Galois . Tanto Abel quanto Galois trabalharam com o que hoje é chamado de campo numérico algébrico , mas não conceberam uma noção explícita de campo, nem de grupo.

Em 1871, Richard Dedekind introduziu, para um conjunto de números reais ou complexos que é fechado sob as quatro operações aritméticas, a palavra alemã Körper , que significa "corpo" ou "corpus" (para sugerir uma entidade organicamente fechada). O termo inglês "campo" foi introduzido por Moore (1893) .

Por campo, entenderemos todo sistema infinito de números reais ou complexos tão fechados em si mesmo e perfeitos que a adição, subtração, multiplicação e divisão de quaisquer dois desses números novamente resulta em um número do sistema.

-  Richard Dedekind, 1871

Em 1881, Leopold Kronecker definiu o que chamou de domínio da racionalidade , que é um campo de frações racionais em termos modernos. A noção de Kronecker não abrangia o campo de todos os números algébricos (que é um campo no sentido de Dedekind), mas, por outro lado, era mais abstrata do que a de Dedekind, pois não fazia suposições específicas sobre a natureza dos elementos de um campo. Kronecker interpretou um campo como Q (π) abstratamente como o campo de função racional Q ( X ) . Antes disso, exemplos de números transcendentais eram conhecidos desde o trabalho de Joseph Liouville em 1844, até Charles Hermite (1873) e Ferdinand von Lindemann (1882) provarem a transcendência de e e π , respectivamente.

A primeira definição clara de um campo abstrato deve-se a Weber (1893) . Em particular, a noção de Heinrich Martin Weber incluiu o campo F _p . Giuseppe Veronese (1891) estudou o campo das séries de potências formais, o que levou Hensel (1904) a introduzir o campo dos números p -adicos. Steinitz (1910) sintetizou o conhecimento da teoria do campo abstrato acumulado até agora. Ele estudou axiomaticamente as propriedades dos campos e definiu muitos conceitos teóricos de campo importantes. A maioria dos teoremas mencionados nas seções Teoria de Galois , Construindo campos e Noções elementares podem ser encontrados no trabalho de Steinitz. Artin e Schreier (1927) ligaram a noção de ordenações em um campo e, portanto, a área de análise, a propriedades puramente algébricas. Emil Artin desenvolveu novamente a teoria de Galois de 1928 a 1942, eliminando a dependência do teorema do elemento primitivo .

Construindo campos

Construindo campos de anéis

Um anel comutativo é um conjunto, equipado com uma operação de adição e multiplicação, satisfazendo todos os axiomas de um corpo, exceto pela existência de inversos multiplicativos a ⁻¹ . Por exemplo, os inteiros Z formam um anel comutativo, mas não um campo: o recíproco de um inteiro n não é ele próprio um inteiro, a menos que n = ± 1 .

Na hierarquia de estruturas algébricas, os campos podem ser caracterizados como os anéis comutativos R nos quais cada elemento diferente de zero é uma unidade (o que significa que cada elemento é invertível). Da mesma forma, os campos são os anéis com conmutativos precisamente duas distintas ideais , (0) e R . Os campos também são precisamente os anéis comutativos nos quais (0) é o único ideal primo .

Dado um anel comutativo R , existem duas maneiras de construir um campo relacionado a R , ou seja, duas maneiras de modificar R de modo que todos os elementos não nulos se tornem invertíveis: formando o campo de frações e formando campos residuais. O campo das frações de Z é Q , os racionais, enquanto os campos residuais de Z são os campos finitos F _p .

Campo de frações

Dado um domínio integral R , seu campo de frações Q ( R ) é construído com as frações de dois elementos de R exatamente como Q é construído a partir dos inteiros. Mais precisamente, os elementos de Q ( R ) são as frações a / b onde a e b estão em R , e b ≠ 0 . Duas fracções de um / b e c / d são iguais se e somente se o anúncio = bc . A operação nas frações funciona exatamente como nos números racionais. Por exemplo,

${\ displaystyle {\ frac {a} {b}} + {\ frac {c} {d}} = {\ frac {ad + bc} {bd}}.}$

É simples mostrar que, se o anel for um domínio integral, o conjunto das frações forma um campo.

O campo F ( x ) das frações racionais sobre um campo (ou domínio integral) F é o campo das frações do anel polinomial F [ x ] . O campo F (( x )) da série Laurent

${\ displaystyle \ sum _ {i = k} ^ {\ infty} a_ {i} x ^ {i} \ (k \ in \ mathbb {Z}, a_ {i} \ in F)}$

sobre um campo F é o campo de frações do anel F [[ x ]] das séries de potências formais (em que k ≥ 0 ). Uma vez que qualquer série de Laurent é uma fração de uma série de potências dividida por uma potência de x (em oposição a uma série de potências arbitrária), a representação de frações é menos importante nesta situação.

Campos de resíduos

Em adição ao campo das fracções, que incorporações R injectively num campo, um campo pode ser obtido a partir de um anel conmutativo R por meio de um mapa sobrejetivo para um campo F . Qualquer campo obtido desta maneira é um quociente P / m , em que m é um máximo ideal de R . Se R tem apenas um máximo ideal m , este campo é chamado o campo resíduo de R .

O ideal gerado por um único polinômio f no anel polinomial R = E [ X ] (sobre um campo E ) é máximo se e somente se f for irredutível em E , ou seja, se f não pode ser expresso como o produto de dois polinômios em E [ X ] de menor grau . Isso produz um campo

F = E [ X ] / ( f ( X )).

Este campo F contém um elemento x (ou seja, a classe residual de X ) que satisfaz a equação

f ( x ) = 0 .

Por exemplo, C é obtido a partir de R por adjacente a unidade imaginária símbolo i , que satisfaz f ( i ) = 0 , em que f ( X ) = X ² + 1 . Além disso, f é irredutível sobre R , o que implica que o mapa que envia um polinomial f ( X ) ε R [ X ] para f ( i ) produz um isomorfismo

${\ displaystyle \ mathbf {R} [X] / \ left (X ^ {2} +1 \ right) \ {\ stackrel {\ cong} {\ longrightarrow}} \ \ mathbf {C}.}$

Construindo campos dentro de um campo maior

Os campos podem ser construídos dentro de um determinado campo de contêiner maior. Suponha dado um campo E , e um campo F contendo E como um subcampo. Para qualquer elemento x de F , existe um menor subcampo de F contendo E e x , chamado de subcampo de F gerado por x e denotado por E ( x ) . A passagem de E a E ( x ) é referido por adjacente um elemento de E . Mais geralmente, para um subconjunto S ⊂ F , há um subcampo mínimo de F contendo E e S , denotado por E ( S ) .

O compositum de dois subcampos E e E ' de algum campo F é o menor subcampo de F contendo E e E'. O compositum pode ser utilizado para construir o maior subcampo de F satisfazer uma determinada propriedade, por exemplo, a maior subcampo de F , o qual é, na língua introduzida abaixo, ao longo algébrica E .

Extensões de campo

A noção de um subcampo E ⊂ F também pode ser considerada do ponto de vista oposto, referindo-se a F sendo uma extensão de campo (ou apenas extensão) de E , denotado por

F / E ,

e leia " F sobre E ".

Um ponto de referência de base de uma extensão de campo é o seu grau [ F  : E ] , isto é, a dimensão de F como um E espaço -vector. Satisfaz a fórmula

[ G  : E ] = [ G  : F ] [ F  : E ] .

Extensões cujo grau é finito são chamadas de extensões finitas. As extensões C / R e F ₄ / F ₂ são de grau 2, enquanto R / Q é uma extensão infinita.

Extensões algébricas

Uma noção fundamental no estudo das extensões de campo F / E são os elementos algébricos . Um elemento é algébrico sobre E se for a raiz de um polinômio com coeficientes em E , ou seja, se satisfizer uma equação polinomial${\ displaystyle x \ in F}$

e _n x ⁿ + e _{n −1} x ^{n −1} + ⋯ + e ₁ x + e ₀ = 0 ,

com e _n , ..., e ₀ em E e e _n ≠ 0 . Por exemplo, a unidade imaginária i em C é algébrica sobre R , e mesmo sobre Q , uma vez que satisfaz a equação

i ² + 1 = 0 .

Uma extensão de campo em que cada elemento de F é algébrico em relação a E é chamada de extensão algébrica . Qualquer extensão finita é necessariamente algébrica, como pode ser deduzido da fórmula de multiplicatividade acima.

O subcampo E ( x ) gerado por um elemento x , como acima, é uma extensão algébrica de E se e somente se x for um elemento algébrico. Ou seja, se x é algébrico, todos os outros elementos de E ( x ) também são necessariamente algébricos. Além disso, o grau da extensão E ( x ) / E , ou seja, a dimensão de E ( x ) como um espaço vetorial E , é igual ao grau mínimo n tal que existe uma equação polinomial envolvendo x , como acima. Se este grau for n , então os elementos de E ( x ) têm a forma

${\ displaystyle \ sum _ {k = 0} ^ {n-1} a_ {k} x ^ {k}, \ \ a_ {k} \ in E.}$

Por exemplo, o campo Q ( i ) dos racionais gaussianos é o subcampo de C que consiste em todos os números da forma a + bi onde a e b são números racionais: somas da forma i ² (e da mesma forma para expoentes superiores) don tem que ser considerado aqui, uma vez que a + bi + ci ² pode ser simplificado para a - c + bi .

Bases da transcendência

O campo acima mencionado de fracções racionais E ( X ) , onde X é um indeterminado , não é uma extensão algébrica de E dado que não existe equação polinomial com coeficientes em E cuja zero é X . Elementos, como X , que não são algébricos são chamados de transcendentais . Informalmente falando, o indeterminado X e seus poderes não interagem com elementos de E . Uma construção semelhante pode ser realizada com um conjunto de indeterminados, em vez de apenas um.

Mais uma vez, a extensão de campo E ( x ) / E discutida acima é um exemplo chave: se x não é algébrico (ou seja, x não é a raiz de um polinômio com coeficientes em E ), então E ( x ) é isomórfico a E ( X ) . Este isomorfismo é obtido substituindo x por X em frações racionais.

Um subconjunto S de um campo F é uma base de transcendência se for algebricamente independente (não satisfaz nenhuma relação polinomial) sobre E e se F for uma extensão algébrica de E ( S ) . Qualquer extensão de campo F / E tem uma base de transcendência. Assim, as extensões de campo podem ser divididas em outras da forma E ( S ) / E ( extensões puramente transcendentais ) e extensões algébricas.

Operações de fechamento

Um campo é algebricamente fechado se não tiver extensões algébricas estritamente maiores ou, de forma equivalente, se houver equação polinomial

f _n x ⁿ + f _{n −1} x ^{n −1} + ⋯ + f ₁ x + f ₀ = 0 , com coeficientes f _n , ..., f ₀ ∈ F , n > 0 ,

tem uma solução x £ F . Pelo teorema fundamental da álgebra , C é algebraicamente fechado, ou seja, qualquer equação polinomial com coeficientes complexos tem uma solução complexa. Os números racionais e reais não são fechados algebricamente, uma vez que a equação

x ² + 1 = 0

não tem nenhuma solução racional ou real. Um campo contendo F é chamado de fechamento algébrico de F se for algébrico sobre F (grosso modo, não muito grande em comparação com F ) e for algébricamente fechado (grande o suficiente para conter soluções de todas as equações polinomiais).

Pelo acima, C representa um fecho algébrico de R . A situação que o fecho algébrico é uma extensão finita do campo F é bastante especial: pelo teorema Artin-Schreier , o grau de esta extensão é, necessariamente, 2, e F é elementaridade equivalente a R . Esses campos também são conhecidos como campos fechados reais .

Qualquer campo F tem um fechamento algébrico, que é, além disso, único até isomorfismo (não único). É comumente referido como o fecho algébrico e denotado F . Por exemplo, o fechamento algébrico Q de Q é chamado de campo de números algébricos . O campo F é geralmente bastante implícito, pois sua construção requer o lema do ultrafiltro , um axioma da teoria dos conjuntos que é mais fraco do que o axioma de escolha . Nesse sentido, o fechamento algébrico de F _q é excepcionalmente simples. É a união dos campos finitos contendo F _q (os de ordem q ⁿ ). Para qualquer campo F algebricamente fechado de característica 0, o fechamento algébrico do campo F (( t )) da série de Laurent é o campo da série de Puiseux , obtido por raízes adjacentes de t .

Campos com estrutura adicional

Uma vez que os campos são onipresentes na matemática e além, vários refinamentos do conceito foram adaptados às necessidades de áreas matemáticas específicas.

Campos ordenados

Um campo F é chamado um campo ordenada se quaisquer dois elementos podem ser comparadas, de modo que x + y ≥ 0 e xy ≥ 0 quando x ≥ 0 e y ≥ 0 . Por exemplo, os números reais formam um campo ordenado, com a ordem usual  ≥ . O teorema de Artin-Schreier afirma que um campo pode ser ordenado se e somente se for um campo formalmente real , o que significa que qualquer equação quadrática

${\ displaystyle x_ {1} ^ {2} + x_ {2} ^ {2} + \ dots + x_ {n} ^ {2} = 0}$

tem apenas a solução x ₁ = x ₂ = ⋯ = x _n = 0 . O conjunto de todos os pedidos possíveis sobre um campo fixo F é isomorfo para o conjunto de homomorphisms anel do anel Witt W ( F ) de formas quadráticas mais de F , para Z .

Um campo arquimediano é um campo ordenado de forma que para cada elemento existe uma expressão finita

1 + 1 + ⋯ + 1

cujo valor é maior que aquele elemento, ou seja, não existem elementos infinitos. De forma equivalente, o campo não contém infinitesimais (elementos menores do que todos os números racionais); ou, ainda equivalente, o campo é isomorfa a um subcampo de R .

Um campo ordenado é Dedekind completo se todos os limites superiores , inferiores (ver corte de Dedekind ) e limites, que deveriam existir, existem. Mais formalmente, cada subconjunto limitado de F deve ter um limite superior mínimo. Qualquer campo completo é necessariamente Arquimediano, uma vez que em qualquer campo não-Arquimediano não existe nem um maior infinitesimal nem um mínimo racional positivo, de onde a sequência 1/2, 1/3, 1/4, ... , cada elemento do qual é maior do que todo infinitesimal, não tem limite.

Uma vez que cada subcampo adequado dos reais também contém tais lacunas, R é o único campo ordenado completo, até o isomorfismo. Vários resultados fundamentais em cálculo decorrem diretamente dessa caracterização dos reais.

Os hiperreals R ^* formam um campo ordenado que não é arquimediano. É uma extensão dos reais obtidos pela inclusão de números infinitos e infinitesimais. Estes são maiores, respectivamente menores do que qualquer número real. Os hiperreais formam a base fundamental da análise não padronizada .

Campos topológicos

Outro refinamento da noção de um campo é um campo topológico , no qual o conjunto F é um espaço topológico , de modo que todas as operações do campo (adição, multiplicação, os mapas a ↦ - a e a ↦ a ⁻¹ ) são contínuas mapas no que diz respeito à topologia do espaço. A topologia de todos os campos discutidos abaixo é induzida a partir de uma métrica , ou seja, uma função

d  : F × F → R ,

que as medidas de uma distância entre quaisquer dois elementos de F .

O preenchimento de F é outro campo em que, informalmente, as "lacunas" do campo F original são preenchidas, se houver. Por exemplo, qualquer número irracional x , como x = √ 2 , é uma "lacuna" nos racionais Q no sentido de que é um número real que pode ser aproximado arbitrariamente por números racionais p / q , no sentido de que distância de x e p / q dadas pelo valor absoluto | x - p / q | é tão pequeno quanto desejado. A tabela a seguir lista alguns exemplos dessa construção. A quarta coluna mostra um exemplo de sequência zero , ou seja, uma sequência cujo limite (para n → ∞ ) é zero.

Campo	Métrica	Conclusão	seqüência zero
Q	| x - y | ( valor absoluto usual )	R	1 / n
Q	obtido usando a avaliação p -adic , para um número primo p	Q p ( números p -adic )	p n
F ( t ) ( F qualquer campo)	obtido usando a avaliação t -adic	F (( t ))	t n

O campo Q _p é usado na teoria dos números e na análise p -adic . O fechamento algébrico Q _p carrega uma norma única estendendo a de Q _p , mas não é completo. A conclusão desse fechamento algébrico, no entanto, é fechada algebricamente. Por causa de sua analogia aproximada com os números complexos, às vezes é chamado de campo de completações métricas e fechamentos algébricos | números p-ádicos complexos e é denotado por C _p .

Campos locais

Os seguintes campos topológicos são chamados de campos locais :

• extensões finitas de Q _p (campos locais de característica zero)
• extensões finitas de F _p (( t )) , o campo da série de Laurent sobre F _p (campos locais de característica p ).

Esses dois tipos de campos locais compartilham algumas semelhanças fundamentais. Nessa relação, os elementos p ∈ Q _p e t ∈ F _p (( t )) (referidos como uniformizador ) correspondem entre si. A primeira manifestação disso está em um nível elementar: os elementos de ambos os campos podem ser expressos como séries de potências no uniformizador, com coeficientes em F _p . (No entanto, uma vez que a adição em Q _p é feita usando o carregamento , o que não é o caso em F _p (( t )) , esses campos não são isomórficos.) Os seguintes fatos mostram que essa semelhança superficial é muito mais profunda:

• Qualquer afirmação de primeira ordem que seja verdadeira para quase todos os Q _p também é verdadeira para quase todos os F _p (( t )) . Uma aplicação disso é o teorema de Ax-Kochen que descreve zeros de polinômios homogêneos em Q _p .
• Extensões igualmente ramificadas de ambos os campos estão em bijeção uma com a outra.
• A junção de raízes arbitrárias de p- potência de p (em Q _p ), respectivamente de t (em F _p (( t )) ), produz extensões (infinitas) desses campos conhecidos como campos perfetóides . Surpreendentemente, os grupos de Galois desses dois campos são isomórficos, o que é o primeiro vislumbre de um paralelo notável entre esses dois campos:
  $${\ displaystyle \ operatorname {Gal} \ left (\ mathbf {Q} _ {p} \ left (p ^ {1 / p ^ {\ infty}} \ right) \ right) \ cong \ operatorname {Gal} \ left (\ mathbf {F} _ {p} ((t)) \ left (t ^ {1 / p ^ {\ infty}} \ right) \ right).}$$

  

Campos diferenciais

Os campos diferenciais são campos equipados com uma derivação , ou seja, permitem obter derivadas de elementos no campo. Por exemplo, o campo R ( X ), junto com a derivada padrão dos polinômios, forma um campo diferencial. Esses campos são centrais para a teoria diferencial de Galois , uma variante da teoria de Galois que lida com equações diferenciais lineares .

Teoria de Galois

A teoria de Galois estuda extensões algébricas de um campo estudando a simetria nas operações aritméticas de adição e multiplicação. Uma noção importante nesta área é a das extensões finitas de Galois F / E , que são, por definição, aquelas que são separáveis e normais . O teorema do elemento primitivo mostra que as extensões separáveis ​​finitas são necessariamente simples , ou seja, da forma

F = E [ X ] / f  ( X ) ,

onde f é um polinômio irredutível (como acima). Para tal extensão, ser normal e separável significa que todos os zeros de f estão contidos em F e que f possui apenas zeros simples. A última condição é sempre satisfeita se E tiver a característica 0.

Para uma extensão de Galois finita, o grupo de Galois Gal ( F / E ) é o grupo de automorfismos de campo de F que são triviais em E (ou seja, as bijeções σ  : F → F que preservam adição e multiplicação e que enviam elementos de E para eles mesmos). A importância deste grupo deriva do teorema fundamental da teoria de Galois , que constrói uma explícita correspondência de um-para-um entre o conjunto de subgrupos de Gal ( F / E ) e o conjunto de extensões intermédias da extensão F / E . Por meio dessa correspondência, as propriedades teóricas dos grupos se traduzem em fatos sobre os campos. Por exemplo, se o grupo de Galois de uma extensão de Galois como acima não puder ser resolvido (não pode ser construído a partir de grupos abelianos ), então os zeros de f não podem ser expressos em termos de adição, multiplicação e radicais, ou seja, expressões envolvendo . Por exemplo, os grupos simétricos S _n não são solucionáveis ​​para n ≥ 5 . Consequentemente, como pode ser mostrado, os zeros dos polinômios a seguir não são expressos por somas, produtos e radicais. Para o último polinômio, esse fato é conhecido como teorema de Abel-Ruffini : ${\ displaystyle {\ sqrt [{n}] {\}}}$

f ( X ) = X ⁵ - 4 X + 2 (e E = Q ),

f ( X ) = X ⁿ + a _{n −1} X ^{n −1} + ⋯ + a ₀ (onde f é considerado um polinômio em E ( a ₀ , ..., a _{n −1} ) , para alguns indeterminados a _i , E é qualquer campo e n ≥ 5 ).

O produto tensorial dos campos geralmente não é um campo. Por exemplo, uma extensão finita F / E de grau n é uma extensão de Galois se e somente se houver um isomorfismo de F- álgebras

F ⊗ _E F ≅ F ⁿ .

Este fato é o início da teoria de Galois de Grothendieck , uma extensão de longo alcance da teoria de Galois aplicável a objetos algebro-geométricos.

Invariantes de campos

Os invariantes básicos de um campo F incluem a característica e o grau de transcendência de F sobre seu campo principal. O último é definido como o número máximo de elementos em F que são algebricamente independentes sobre o campo primo. Dois campos algebricamente fechados E e F são isomórficos precisamente se esses dois dados concordarem. Isso implica que quaisquer dois incontáveis campos algebricamente fechados com a mesma cardinalidade e a mesma característica são isomórficos. Por exemplo, Q _p , C _p e C são isomórficos (mas não isomórficos como campos topológicos).

Teoria modelo de campos

Na teoria do modelo , um ramo da lógica matemática , dois campos E e F são chamados de equivalente elementar se todas as afirmações matemáticas que são verdadeiras para E também são verdadeiras para F e vice-versa. As declarações matemáticas em questão devem ser sentenças de primeira ordem (envolvendo 0, 1, a adição e multiplicação). Um exemplo típico, para n > 0 , n um inteiro, é

φ ( E ) = "qualquer polinômio de grau n em E tem um zero em E "

O conjunto dessas fórmulas para todos os n expressa que E é algebricamente fechado. O princípio de Lefschetz afirma que C é elementarmente equivalente a qualquer campo F algebricamente fechado de zero característico. Além disso, qualquer afirmação fixa φ vale em C se e somente se vale em qualquer campo algebraicamente fechado de característica suficientemente alta.

Se U for um ultrafiltro em um conjunto I e F _i for um campo para cada i em I , o ultraproduto de F _i em relação a U será um campo. É denotado por

ulim _{i → ∞} F _i ,

uma vez que se comporta de várias maneiras como um limite dos campos F _i : o teorema de Łoś afirma que qualquer afirmação de primeira ordem válida para todos, exceto para finitamente muitos F _i , também é válida para o ultraproduto. Aplicado à frase acima φ , isso mostra que há um isomorfismo

${\ displaystyle \ operatorname {ulim} _ {p \ to \ infty} {\ overline {\ mathbf {F}}} _ {p} \ cong \ mathbf {C}.}$

O teorema Ax-Kochen mencionado acima também segue a partir disso e um isomorfismo dos ultraprodutos (em ambos os casos, em todos os primos p )

ulim _p Q _p ≅ ulim _p F _p (( t )) .

Além disso, a teoria do modelo também estuda as propriedades lógicas de vários outros tipos de campos, como campos fechados reais ou campos exponenciais (que são equipados com uma função exponencial exp: F → F ^x ).

O grupo absoluto de Galois

Para os campos que não são algebricamente fechados (ou não separável fechado), o grupo de Galois absoluto Gal ( F ) é fundamentalmente importante: que se estende no caso de extensões de Galois finitos descritos acima, esse grupo governa todos os extensão separável finitos de F . Por meio elementares, o grupo Gal ( F _q ) pode ser demonstrado que o grupo de prüfer , a conclusão profinitos de Z . Esta afirmação inclui o fato de que as únicas extensões algébricas de Gal ( F _q ) são os campos Gal ( F _{q ⁿ} ) para n > 0 , e que os grupos de Galois dessas extensões finitas são dados por

Gal ( F _{q ⁿ} / F _q ) = Z / N Z .

Uma descrição em termos de geradores e relações também é conhecida para os grupos de Galois de campos de números p -adicos (extensões finitas de Q _p ).

As representações dos grupos de Galois e de grupos relacionados, como o grupo Weil, são fundamentais em muitos ramos da aritmética, como o programa de Langlands . O estudo cohomológico de tais representações é feito usando a cohomologia de Galois . Por exemplo, o grupo Brauer , que é classicamente definido como o grupo de F- álgebras simples centrais , pode ser reinterpretado como um grupo de cohomologia de Galois, a saber

Br ( F ) = H ² ( F , G _m ) .

Teoria K

A teoria K de Milnor é definida como

${\ displaystyle K_ {n} ^ {M} (F) = F ^ {\ times} \ otimes \ cdots \ otimes F ^ {\ times} / \ left \ langle x \ otimes (1-x) \ mid x \ em F \ setminus \ {0,1 \} \ right \ rangle.}$

O teorema do isomorfismo de resíduo de norma , provado por volta de 2000 por Vladimir Voevodsky , relaciona isso à cohomologia de Galois por meio de um isomorfismo

${\ displaystyle K_ {n} ^ {M} (F) / p = H ^ {n} (F, \ mu _ {l} ^ {\ otimes n}).}$

A teoria algébrica K está relacionada ao grupo de matrizes invertíveis com coeficientes no campo dado. Por exemplo, o processo de tomar o determinante de uma matriz invertível leva a um isomorfismo K ₁ ( F ) = F ^× . O teorema de Matsumoto mostra que K ₂ ( F ) concorda com K ₂ ^M ( F ). Em graus mais elevados, a teoria K diverge da teoria K de Milnor e permanece difícil de computar em geral.

Formulários

Álgebra Linear e Álgebra Comutativa

Se a ≠ 0 , então a equação

ax = b

tem uma solução única x em um campo F , a saber: Esta consequência imediata da definição de um campo é fundamental na álgebra linear . Por exemplo, é um ingrediente essencial da eliminação gaussiana e da prova de que qualquer espaço vetorial tem uma base . ${\ displaystyle x = a ^ {- 1} b.}$

A teoria dos módulos (o análogo dos espaços vetoriais sobre anéis em vez de campos) é muito mais complicada, porque a equação acima pode ter várias ou nenhuma solução. Em determinados sistemas de equações lineares sobre um anel são muito mais difíceis de resolver do que no caso dos campos, mesmo no caso especialmente simples do anel dos inteiros. ${\ displaystyle \ mathbb {Z}}$

Campos finitos: criptografia e teoria da codificação

Uma rotina criptográfica amplamente aplicada usa o fato de que a exponenciação discreta, ou seja, a computação

a ⁿ = a ⋅ a ⋅ ⋯ ⋅ a ( n fatores, para um inteiro n ≥ 1 )

em um (grande) campo finito F _q pode ser executado de forma muito mais eficiente do que o logaritmo discreto , que é a operação inversa, ou seja, determinar a solução n para uma equação

a ⁿ = b .

Na criptografia de curva elíptica , a multiplicação em um corpo finito é substituída pela operação de adição de pontos em uma curva elíptica , ou seja, as soluções de uma equação da forma

y ² = x ³ + ax + b .

Os campos finitos também são usados ​​na teoria da codificação e combinatória .

Geometria: campo de funções

Funções em um espaço topológico adequado X em um campo k podem ser adicionadas e multiplicadas pontualmente, por exemplo, o produto de duas funções é definido pelo produto de seus valores dentro do domínio:

( f ⋅ g ) ( x ) = f ( x ) ⋅ g ( x ) .

Isso torna essas funções uma álgebra k - comutativa .

Por ter um campo de funções, deve-se considerar álgebras de funções que são domínios integrais . Neste caso, as proporções de duas funções, ou seja, expressões da forma

${\ displaystyle {\ frac {f (x)} {g (x)}},}$

formam um campo, denominado campo de funções.

Isso ocorre em dois casos principais. Quando X é um complexo colector X . Nesse caso, considera-se a álgebra de funções holomórficas , ou seja, funções diferenciadas complexas. Os seus rácios de formar o campo de funções meromorfas sobre X .

O campo de função de uma variedade algébrica X (um objeto geométrico definido como os zeros comuns de equações polinomiais) consiste em proporções de funções regulares , ou seja, proporções de funções polinomiais na variedade. O campo funcional do espaço n- dimensional sobre um campo k é k ( x ₁ , ..., x _n ) , ou seja, o campo consiste em razões de polinômios em n indeterminados. O campo de função de X é o mesmo de qualquer subvariedade densa aberta . Em outras palavras, o campo de função é insensível à substituição de X por uma subvariedade (ligeiramente) menor.

O campo de função é invariante sob isomorfismo e equivalência birracional de variedades. É, portanto, uma ferramenta importante para o estudo de variedades algébricas abstratas e para a classificação de variedades algébricas. Por exemplo, a dimensão , que é igual ao grau de transcendência de k ( X ) , é invariante sob equivalência birracional. Para curvas (ou seja, a dimensão é um), o campo de função k ( X ) é muito próximo de X : se X é suave e adequado (o análogo de ser compacto ), X pode ser reconstruído, até isomorfismo, de seu campo de funções. Em dimensão maior o campo de função lembra menos, mas ainda informações decisivas sobre X . O estudo dos campos de função e seu significado geométrico em dimensões superiores é conhecido como geometria birracional . O programa de modelo mínimo tenta identificar as variedades algébricas mais simples (em um certo sentido preciso) com um campo de função prescrito.

Teoria dos números: campos globais

Os campos globais estão no centro das atenções na teoria dos números algébricos e na geometria aritmética . Eles são, por definição, campos numéricos (extensões finitas de Q ) ou campos de função sobre F _q (extensões finitas de F _q ( t ) ). Quanto aos campos locais, esses dois tipos de campos compartilham várias características semelhantes, embora sejam de característica 0 e característica positiva, respectivamente. Essa analogia de campo de função pode ajudar a moldar expectativas matemáticas, geralmente primeiro entendendo questões sobre campos de função e, posteriormente, tratando do caso de campo numérico. O último costuma ser mais difícil. Por exemplo, a hipótese de Riemann sobre os zeros da função zeta de Riemann (aberta em 2017) pode ser considerada paralela às conjecturas de Weil (comprovada em 1974 por Pierre Deligne ).

Os campos ciclotômicos estão entre os campos numéricos mais intensamente estudados. Eles são da forma Q (ζ _n ) , onde ζ _n é uma raiz n- ésima primitiva da unidade , ou seja, um número complexo que satisfaz ζ ⁿ = 1 e ζ ^m ≠ 1 para todo m < n . Por n ser um primo regular , Kummer usou campos ciclotômicos para provar o Último Teorema de Fermat , que afirma a inexistência de soluções racionais diferentes de zero para a equação

x ⁿ + y ⁿ = z ⁿ .

Os campos locais são completamentos de campos globais. Teorema de Ostrowski afirma que as únicas conclusões de Q , um campo global, são os campos locais Q _p e R . O estudo de questões aritméticas em campos globais pode, às vezes, ser feito examinando-se as questões correspondentes localmente. Essa técnica é chamada de princípio local-global . Por exemplo, o teorema de Hasse-Minkowski reduz o problema de encontrar soluções racionais de equações quadráticas para resolver essas equações em R e Q _p , cujas soluções podem ser facilmente descritas.

Ao contrário dos campos locais, os grupos de Galois de campos globais não são conhecidos. Inverse Galois teoria estudos do problema (não resolvido) se qualquer grupo finito é o grupo de Galois Gal ( F / Q ) por algum campo de número F . A teoria de campo de classes descreve as extensões abelianas , isto é, aquelas com o grupo de Galois abeliano, ou equivalentemente os grupos de Galois abelianizados de campos globais. Uma afirmação clássica, o teorema de Kronecker-Weber , descreve a extensão abeliana máxima de Q ^ab de Q : é o campo

Q (ζ _n , n ≥ 2)

obtido pela união de todas as n- ésimas raízes primitivas da unidade. Jugendtraum de Kronecker pede uma descrição semelhante explícita de F ^ab de campos de número geral F . Para campos quadráticas imaginárias , , d > 0 , a teoria de multiplicação complexa descreve F ^ab usando curvas elípticas . Para campos de números gerais, nenhuma descrição explícita é conhecida. ${\ displaystyle F = \ mathbf {Q} ({\ sqrt {-d}})}$

Noções relacionadas

Além da estrutura adicional de que os campos podem desfrutar, eles admitem várias outras noções relacionadas. Como em qualquer campo 0 ≠ 1, qualquer campo possui pelo menos dois elementos. No entanto, existe um conceito de campo com um elemento , que é sugerido como um limite dos campos finitos F _p , já que p tende a 1. Além dos anéis de divisão, existem várias outras estruturas algébricas mais fracas relacionadas a campos, como quasifields , perto de campos de e semifields .

Existem também classes próprias com estrutura de campo, que às vezes são chamadas de Campos , com F maiúsculo. Os números surreais formam um Campo contendo os reais, e seriam um campo, exceto pelo fato de serem uma classe própria, não um conjunto. Os nimbers , um conceito da teoria dos jogos , também formam esse campo.

Anéis de divisão

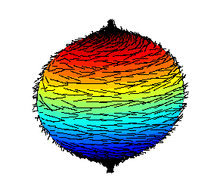
Abandonar um ou vários axiomas na definição de um campo leva a outras estruturas algébricas. Como foi mencionado acima, os anéis comutativos satisfazem todos os axiomas de campos, exceto para inversos multiplicativos. Eliminando, em vez disso, a condição de que a multiplicação é comutativa leva ao conceito de um anel de divisão ou campo inclinado . Os únicos anéis de divisão que são espaços vetoriais R de dimensão finita são o próprio R , C (que é um campo), os quatérnions H (em que a multiplicação é não comutativa) e as octonions O (em que a multiplicação não é nem comutativa nem associativo). Este fato foi comprovado usando métodos de topologia algébrica em 1958 por Michel Kervaire , Raoul Bott e John Milnor . A inexistência de uma álgebra de divisão de dimensão ímpar é mais clássica. Isso pode ser deduzido do teorema da bola cabeluda ilustrado à direita.

Notas

Referências