Teorema do ângulo externo - Exterior angle theorem

O teorema do ângulo externo é a Proposição 1.16 em Elementos de Euclides , que afirma que a medida de um ângulo externo de um triângulo é maior do que qualquer uma das medidas dos ângulos internos remotos. Este é um resultado fundamental na geometria absoluta porque sua prova não depende do postulado paralelo .

Em vários tratamentos de geometria do ensino médio, o termo "teorema do ângulo exterior" foi aplicado a um resultado diferente, a saber, a porção da Proposição 1.32 que afirma que a medida de um ângulo exterior de um triângulo é igual à soma das medidas de os ângulos internos remotos. Este resultado, que depende do postulado paralelo de Euclides, será referido como o "Teorema do ângulo externo da escola secundária" (HSEAT) para distingui-lo do teorema do ângulo externo de Euclides.

Alguns autores referem-se ao "teorema do ângulo externo da escola secundária" como a forma forte do teorema do ângulo externo e ao "teorema do ângulo externo de Euclides" como a forma fraca .

Ângulos externos

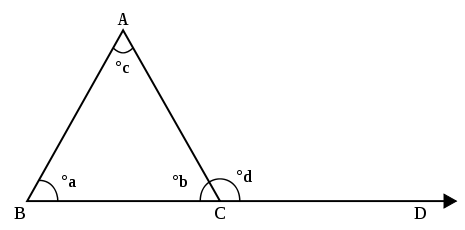
Um triângulo tem três vértices, chamados de vértices . Os lados de um triângulo (segmentos de linha) que se unem em um vértice formam dois ângulos (quatro ângulos se você considerar os lados do triângulo como linhas em vez de segmentos de linha). Apenas um desses ângulos contém o terceiro lado do triângulo em seu interior, e esse ângulo é chamado de ângulo interno do triângulo. Na figura abaixo, os ângulos ∠ABC , ∠BCA e ∠CAB são os três ângulos internos do triângulo. Um ângulo externo é formado estendendo-se um dos lados do triângulo; o ângulo entre o lado estendido e o outro lado é o ângulo externo. Na imagem, o ângulo ∠ACD é um ângulo externo.

Teorema do ângulo exterior de Euclides

A prova da Proposição 1.16 dada por Euclides é freqüentemente citada como um lugar onde Euclides dá uma prova falha.

Euclides prova o teorema do ângulo exterior por:

• construir o ponto médio E do segmento AC,
• desenhe o raio BE,
• construir o ponto F no raio BE de modo que E seja (também) o ponto médio de B e F,
• desenhe o segmento FC.

Por triângulos congruentes podemos concluir que ∠ BAC = ∠ ECF e ∠ ECF é menor que ∠ ECD, ∠ ECD = ∠ ACD, portanto, ∠ BAC é menor que ∠ ACD e o mesmo pode ser feito para o ângulo ∠ CBA dividindo BC ao meio.

A falha está na suposição de que um ponto (F, acima) está "dentro" do ângulo (∠ ACD). Nenhuma razão é fornecida para esta afirmação, mas o diagrama a seguir faz com que pareça uma afirmação verdadeira. Quando um conjunto completo de axiomas para a geometria euclidiana é usado (ver Fundamentos da geometria ), esta afirmação de Euclides pode ser provada.

Inválido em geometria esférica

Triângulos pequenos podem se comportar de maneira quase euclidiana, mas os ângulos externos na base do grande triângulo são de 90 °, uma contradição com o teorema do ângulo externo de Euclides.

O teorema do ângulo exterior não é válido na geometria esférica nem na geometria elíptica relacionada . Considere um triângulo esférico, um de cujos vértices é o Pólo Norte e os outros dois estão no equador . Os lados do triângulo que emanam do Pólo Norte ( grandes círculos da esfera) encontram o equador em ângulos retos, então este triângulo tem um ângulo externo que é igual a um ângulo interno remoto. O outro ângulo interno (no Pólo Norte) pode ser maior que 90 °, enfatizando ainda mais a falha desta afirmação. No entanto, como o teorema do ângulo externo de Euclides é um teorema em geometria absoluta, ele é automaticamente válido em geometria hiperbólica .

Teorema do ângulo exterior da escola secundária

O teorema do ângulo externo do ensino médio (HSEAT) diz que o tamanho de um ângulo externo em um vértice de um triângulo é igual à soma dos tamanhos dos ângulos internos nos outros dois vértices do triângulo (ângulos internos remotos). Portanto, na imagem, o tamanho do ângulo ACD é igual ao tamanho do ângulo ABC mais o tamanho do ângulo CAB .

O HSEAT é logicamente equivalente à afirmação euclidiana de que a soma dos ângulos de um triângulo é 180 °. Se for sabido que a soma das medidas dos ângulos em um triângulo é 180 °, então o HSEAT é provado da seguinte forma:

${\ displaystyle b + d = 180 ^ {\ circ}}$

${\ displaystyle b + d = b + a + c}$

${\ displaystyle \ portanto d = a + c.}$

Por outro lado, se o HSEAT for considerado uma afirmação verdadeira, então:

${\ displaystyle d = a + c}$

${\ displaystyle b + d = 180 ^ {\ circ}}$

${\ displaystyle \ portanto b + a + c = 180 ^ {\ circ}.}$

Ilustração da prova do HSEAT

Provando que a soma das medidas dos ângulos de um triângulo é 180 °.

A prova euclidiana do HSEAT (e simultaneamente o resultado na soma dos ângulos de um triângulo) começa construindo a linha paralela ao lado AB passando pelo ponto C e, em seguida, usando as propriedades dos ângulos correspondentes e ângulos internos alternados de linhas paralelas para obtenha a conclusão como na ilustração.

O HSEAT pode ser extremamente útil ao tentar calcular as medidas de ângulos desconhecidos em um triângulo.

Notas

Referências

• Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry , New York: Marcel Dekker, Inc., ISBN 0-8247-1748-1
• Greenberg, Marvin Jay (1974), Euclidean and Non-Euclidean Geometries / Development and History , San Francisco: WH Freeman, ISBN 0-7167-0454-4
• Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2ª ed. [Fac-símile. Publicação original: Cambridge University Press, 1925] ed.). Nova York: Dover Publications.

(3 vols.): ISBN  0-486-60088-2 (vol. 1), ISBN  0-486-60089-0 (vol. 2), ISBN  0-486-60090-4 (vol. 3).

• Henderson, David W .; Taimiņa, Daina (2005), Experiencing Geometry / Euclidean and Non-Euclidean with History (3rd ed.), Pearson / Prentice-Hall, ISBN 0-13-143748-8
• Venema, Gerard A. (2006), Foundations of Geometry , Upper Saddle River, NJ: Pearson Prentice Hall, ISBN 0-13-143700-3
• Wylie Jr., CR (1964), Foundations of Geometry , Nova York: McGraw-Hill

Referências HSEAT

• Geometria Textbook - Standard IX , Maharashtra Conselho Estadual de Ensino Secundário e Superior Secundário , Pune - 411 005, Índia .
• Geometry Common Core , 'Pearson Education: Upper Saddle River, © 2010, páginas 171-173 | Estados Unidos .
• Wheater, Carolyn C. (2007), Homework Helpers: Geometry , Franklin Lakes, NJ: Career Press, pp. 88–90, ISBN 978-1-56414-936-7.