Castor ocupado - Busy beaver
Na ciência da computação teórica , o jogo do castor ocupado visa encontrar um programa de encerramento de um determinado tamanho que produza a maior saída possível. Uma vez que um programa em loop infinito que produz uma saída infinita é facilmente concebido, tais programas são excluídos do jogo.
Mais precisamente, o jogo do castor ocupado consiste em projetar uma máquina de Turing com alfabeto binário, que grava o máximo de 1s na fita, usando apenas um determinado conjunto de estados. As regras para o jogo de 2 estados são as seguintes:
- a máquina deve ter dois estados além do estado de parada, e
- a fita inicialmente contém apenas 0s.
Um jogador deve conceber uma mesa de transição visando a produção mais longa de 1s na fita enquanto se certifica de que a máquina irá parar eventualmente.
Um n º castor ocupado , BB- n ou simplesmente "castor ocupado" é uma máquina de Turing que vence o Jogo do Castor Ocupado n-estado . Ou seja, ele atinge o maior número de 1s entre todas as outras máquinas de Turing competidoras de n- estados possíveis . A máquina de Turing BB-2 , por exemplo, atinge quatro 1s em seis etapas.
Determinar se uma máquina de Turing arbitrária é um castor ocupado é indecidível . Isso tem implicações na teoria da computabilidade , no problema da parada e na teoria da complexidade . O conceito foi introduzido pela primeira vez por Tibor Radó em seu artigo de 1962, "On Non-Computable Functions".
O jogo
O n jogo castor ocupado -state (ou BB- n jogo ), introduzido em Tibor Radó 1962 papel 's, envolve uma classe de máquinas de Turing , cada membro dos quais é requerido para satisfazer as seguintes especificações de concepção:
- A máquina tem n estados "operacionais" mais um estado Halt, onde n é um número inteiro positivo e um dos n estados é distinguido como o estado inicial. (Normalmente, os estados são rotulados por 1, 2, ..., n , com o estado 1 como o estado inicial, ou por A , B , C , ..., com o estado A como o estado inicial.)
- A máquina usa uma única fita infinita (ou ilimitada) bidirecional.
- O alfabeto da fita é {0, 1}, com 0 servindo como o símbolo em branco.
- A função de transição da máquina leva duas entradas:
- o estado não-parado atual,
- o símbolo na célula da fita atual,
- e produz três resultados:
- um símbolo para sobrescrever o símbolo na célula da fita atual (pode ser o mesmo símbolo que o símbolo sobrescrito),
- uma direção para mover (esquerda ou direita; ou seja, mudar para a célula de fita um lugar à esquerda ou direita da célula atual), e
- um estado para o qual fazer a transição (que pode ser o estado Halt).
- Há, assim, (4 n + 4) 2 n n máquinas de Turing -state satisfazem esta definição, porque a forma geral da fórmula é ( símbolos × instruções × ( estados + 1)) ( símbolos × Unidos ) .
- A função de transição pode ser vista como uma tabela finita de 5 tuplas, cada uma da forma
- (estado atual, símbolo atual, símbolo a ser escrito, direção da mudança, próximo estado).
"Rodar" a máquina consiste em iniciar no estado inicial, com a célula da fita atual sendo qualquer célula de uma fita em branco (toda-0), e então iterar a função de transição até que o estado Halt seja inserido (se houver). Se, e somente se, a máquina finalmente parar, então o número de 1s restantes na fita é chamado de pontuação da máquina .
O n -state castor ocupado (BB- n jogo) é um concurso para encontrar um tal n máquina de Turing -state ter a maior pontuação possível - o maior número de 1s na sua fita depois da parada. Uma máquina que atinge a maior pontuação possível entre todos os n máquinas de Turing -Estado é chamado de n castor ocupado -state, e uma máquina cuja pontuação é apenas o mais alto até agora alcançado (talvez não o maior possível) é chamado de campeão n -state máquina.
Radó exigia que cada máquina inscrita no concurso fosse acompanhada de uma declaração do número exato de passos necessários para atingir o estado Parado, permitindo assim que a pontuação de cada inscrição fosse verificada (em princípio) rodando a máquina para o número indicado de etapas. (Se as entradas consistissem apenas em descrições de máquina, então o problema de verificar cada entrada potencial é indecidível, porque é equivalente ao conhecido problema de parada - não haveria uma maneira eficaz de decidir se uma máquina arbitrária eventualmente para.)
Funções relacionadas
A função do castor ocupado Σ
A função de castor ocupado quantifica a pontuação máxima atingível por um castor ocupado em uma determinada medida. Esta é uma função não computável . Além disso, uma função de castor ocupado pode crescer mais rápido assintoticamente do que qualquer função computável.
A função do castor ocupado, Σ: ℕ → ℕ, é definida de tal modo que Σ ( n ) é a pontuação máxima atingível (o número máximo de 1s finalmente na fita) entre todas as máquinas de Turing de 2 símbolos n- estados de parada acima- tipo descrito, quando iniciado em uma fita em branco.
É claro que Σ é uma função bem definida: para cada n , há no máximo muitas máquinas de Turing de n- estados como acima, até o isomorfismo, portanto, no máximo, muitos tempos de execução possíveis.
Essa sequência infinita Σ é a função do castor ocupado , e qualquer máquina de Turing M de 2 símbolos de n -estado para a qual σ ( M ) = Σ ( n ) (isto é, que atinge a pontuação máxima) é chamada de castor ocupado . Observe que, para cada n , existem pelo menos quatro castores ocupados de n estados (porque, dado qualquer castor ocupado de n estados, outro é obtido meramente mudando a direção da mudança em uma transição interrompida, outro mudando todas as mudanças de direção para o seu oposto , e o final mudando a direção de parada do castor ocupado totalmente trocado).
Não computabilidade
O artigo de Radó de 1962 provou que se f : ℕ → ℕ é qualquer função computável , então Σ ( n )> f (n) para todo n suficientemente grande e, portanto, que Σ não é uma função computável.
Além disso, isso implica que é indecidível por um algoritmo geral se uma máquina de Turing arbitrária é um castor ocupado. (Tal algoritmo não pode existir, porque sua existência permitiria que Σ fosse calculado, o que é uma impossibilidade comprovada. Em particular, tal algoritmo poderia ser usado para construir outro algoritmo que calcularia Σ da seguinte forma: para qualquer n dado , cada um dos as finitas máquinas de Turing de 2 símbolos de n- estados seriam testadas até que um castor ocupado de n- estados fosse encontrado; essa máquina de castor ocupada seria então simulada para determinar sua pontuação, que é por definição Σ ( n ).)
Embora Σ ( n ) seja uma função incomputável, existem alguns n pequenos para os quais é possível obter seus valores e provar que estão corretos. Não é difícil mostrar que Σ (0) = 0, Σ (1) = 1, Σ (2) = 4, e com dificuldade progressivamente maior pode ser mostrado que Σ (3) = 6 e Σ (4) = 13 (sequência A028444 no OEIS ). Σ ( n ) ainda não foi determinado para qualquer instância de n > 4, embora os limites inferiores tenham sido estabelecidos (consulte a seção Valores conhecidos abaixo).
Em 2016, Adam Yedidia e Scott Aaronson obtiveram o primeiro limite superior (explícito) no n mínimo para o qual Σ ( n ) é improvável em ZFC . Para isso, eles construíram uma máquina de Turing de 7910 estados cujo comportamento não pode ser comprovado com base nos axiomas usuais da teoria dos conjuntos (teoria dos conjuntos de Zermelo-Fraenkel com o axioma da escolha ), sob hipóteses de consistência razoável ( propriedade estacionária de Ramsey ). Posteriormente, foi reduzido para 1919 estados, com a eliminação da dependência da propriedade estacionária de Ramsey, e posteriormente para 748 estados.
Complexidade e impossibilidade de comprovação de Σ
Uma variante da complexidade de Kolmogorov é definida como segue [cf. Boolos, Burgess & Jeffrey, 2007]: A complexidade de um número n é o menor número de estados necessários para uma máquina de Turing classe BB que para com um único bloco de n 1s consecutivos em uma fita inicialmente em branco. A variante correspondente do teorema da incompletude de Chaitin afirma que, no contexto de um determinado sistema axiomático para os números naturais, existe um número k tal que nenhum número específico pode ser provado como tendo complexidade maior do que k e, portanto, nenhum limite superior específico pode ser provado para Σ ( k ) (o último é porque "a complexidade de n é maior que k " seria provado se " n > Σ ( k )" fosse provado). Conforme mencionado na referência citada, para qualquer sistema axiomático de "matemática comum", o menor valor k para o qual isso é verdadeiro é muito menor que 10 ↑↑ 10 ; conseqüentemente, no contexto da matemática comum, nem o valor nem qualquer limite superior de Σ (10 ↑↑ 10) podem ser provados. ( O primeiro teorema da incompletude de Gödel é ilustrado por este resultado: em um sistema axiomático da matemática comum, há uma sentença verdadeira, mas improvável, da forma "Σ (10 ↑↑ 10) = n ", e existem infinitas frases não comprováveis da forma "Σ (10 ↑↑ 10) < n ".)
Mudanças máximas função S
Além da função Σ, Radó [1962] introduziu outra função extrema para a classe BB das máquinas de Turing, a função de deslocamento máximo , S , definida como segue:
- s ( M ) = o número de deslocamentos que M faz antes de parar, para qualquer M em E n ,
- S ( n ) = máx { s ( M ) | M ∈ E n } = o maior número de mudanças feitas por qualquer máquina de Turing de 2 símbolos de n -estado.
Como essas máquinas de Turing precisam ter uma mudança em cada transição ou "etapa" (incluindo qualquer transição para um estado Halt), a função de mudanças máximas é ao mesmo tempo uma função de etapas máximas.
Radó mostrou que S é não-computável pela mesma razão que Σ é não-computável - ele cresce mais rápido do que qualquer função computável. Ele provou isso simplesmente observando que para cada n , S ( n ) ≥ Σ ( n ). Cada turno pode escrever 0 ou 1 na fita, enquanto Σ conta um subconjunto dos turnos que escreveram 1, ou seja, aqueles que não foram sobrescritos no momento em que a máquina de Turing parou; consequentemente, S cresce pelo menos tão rápido quanto Σ, que já havia se mostrado crescer mais rápido do que qualquer função computável.
A sequência de ligação entre Σ e S foi usado por Lin & Radó [ Estudos de computador de problemas da máquina de Turing , 1965] para provar que Σ (3) = 6: Para um dado n , se S ( n ) é conhecido, em seguida, todos os n -state As máquinas de Turing podem (em princípio) ser executadas por até S ( n ) etapas, ponto em que qualquer máquina que ainda não tenha parado nunca irá parar. Nesse ponto, observando quais máquinas pararam com mais 1s na fita (ou seja, os castores ocupados), obtém-se de suas fitas o valor de Σ ( n ). A abordagem usada por Lin & Radó para o caso de n = 3 foi conjeturar que S (3) = 21, e então simular todas as máquinas de 3 estados essencialmente diferentes por até 21 etapas. Ao analisar o comportamento das máquinas que não pararam em 21 etapas, eles conseguiram mostrar que nenhuma dessas máquinas pararia, provando assim a conjectura de que S (3) = 21, e determinando que Σ (3) = 6 por o procedimento que acabamos de descrever.
Desigualdades relacionadas a Σ e S incluem o seguinte (de [Ben-Amram, et al., 1996]), que são válidas para todos n ≥ 1 :
e um limite melhorado assintoticamente (de [Ben-Amram, Petersen, 2002]): existe uma constante c , tal que para todo n ≥ 2 ,
tende a ficar perto do quadrado de e, de fato, muitas máquinas dão menos de .
Valores conhecidos para Σ e S
A partir de 2016, os valores da função para Σ ( n ) e S ( n ) só são conhecidos exatamente para n <5.
O atual (a partir de 2018) campeão de castores ocupados em 5 estados produz 4098 1s, usando47 176 870 passos (descobertos por Heiner Marxen e Jürgen Buntrock em 1989), mas permanecem 18 ou 19 (possivelmente menos de 10, veja abaixo) máquinas com comportamento não regular que se acredita nunca parar, mas que não foi provado que parem correr infinitamente. A Skelet lista 42 ou 43 máquinas não comprovadas, mas 24 já foram comprovadas. As máquinas restantes foram simuladas para 81,8 bilhões de passos, mas nenhuma parou. Daniel Briggs também provou algumas máquinas. Outra fonte disse que 98 máquinas ainda não foram testadas. Há uma análise de holdouts. Portanto, é provável que Σ (5) = 4098 e S (5) = 47176870, mas isso permanece não comprovado, e não se sabe se há alguma validação restante (em 2018). No momento, o campeão estadual recorde produz mais de3,515 × 10 18 267 1s (exatamente (25 × 4 30341 +23) / 9), usando mais7,412 × 10 36 534 etapas (encontrado por Pavel Kropitz em 2010). Conforme observado acima, essas são máquinas de Turing de 2 símbolos.
Uma simples extensão da máquina de 6 estados leva a uma máquina de 7 estados que escreverá mais de 10 10 10 1018 705 353 1s para a fita, mas há, sem dúvida, máquinas de 7 estados muito mais ocupadas. No entanto, outros caçadores de castores ocupados têm diferentes conjuntos de máquinas.
Milton Green, em seu artigo de 1964 "Um limite inferior na função Sigma de Rado para máquinas de Turing binárias", construiu um conjunto de máquinas de Turing demonstrando que
onde ↑ é a notação de seta para cima de Knuth e A é a função de Ackermann .
Assim
(com 3 3 3 = 7 625 597 484 987 termos na torre exponencial), e
onde o número g 1 é o enorme valor inicial na sequência que define o número de Graham .
Em 1964, Milton Green desenvolveu um limite inferior para a função Busy Beaver que foi publicado nos anais do simpósio IEEE de 1964 sobre teoria de circuitos de comutação e design lógico. Heiner Marxen e Jürgen Buntrock o descreveram como "um limite inferior não trivial (não recursivo primitivo)". Esse limite inferior pode ser calculado, mas é muito complexo para ser expresso como uma única expressão em termos de n. Quando n = 8, o método dá Σ (8) ≥ 3 × (7 × 3 92 - 1) / 2 ≈ 8,248 × 10 44 .
Pode ser derivado dos limites inferiores atuais que:
Em contraste, o melhor limite inferior da corrente (em 2018) em Σ (6) é 10 18 267 , que é maior do que o limite inferior dado pela fórmula de Green, 3 3 = 27 (que é minúsculo em comparação). Na verdade, é muito maior do que o limite inferior: 3 ↑↑ 3 = 3 3 3 =7 625 597 484 987 , que é o primeiro limite inferior de Green para Σ (8), e também muito maior do que o segundo limite inferior: 3 × (7 × 3 92 −1) / 2.
Σ (7) é da mesma forma muito, muito maior do que o limite inferior comum atual 3 31 (quase 618 trilhões), então o segundo limite inferior também é muito, muito fraco.
Prova de incomputabilidade de S ( n ) e Σ ( n )
Suponha que S ( n ) seja uma função computável e deixe EvalS denotar uma TM, avaliando S ( n ). Dada uma fita com n 1s, ela produzirá S ( n ) 1s na fita e então parará. Deixe Clean denotar uma máquina de Turing que limpa a sequência de 1s inicialmente escrita na fita. Deixe Double denotar uma máquina de Turing avaliando a função n + n . Dada uma fita com n 1s, ela produzirá 2 n 1s na fita e então parará. Vamos criar a composição Double | EvalS | Limpe e seja n 0 o número de estados desta máquina. Deixe Create_n 0 denotar uma máquina de Turing criando n 0 1s em uma fita inicialmente em branco. Esta máquina pode ser construída de maneira trivial para ter n 0 estados (o estado i escreve 1, move a cabeça para a direita e muda para o estado i + 1, exceto o estado n 0 , que para). Seja N a soma n 0 + n 0 .
Deixe BadS denotar a composição Create_n 0 | Double | EvalS | Limpo . Observe que esta máquina possui N estados. Começando com uma fita inicialmente em branco, ela primeiro cria uma sequência de n 0 1s e, em seguida, a duplica, produzindo uma sequência de N 1s. Então BadS produzirá S ( N ) 1s na fita e, por fim, apagará todos os 1s e então parará. Mas a fase de limpeza continuará pelo menos S ( N ) etapas, portanto o tempo de trabalho de BadS é estritamente maior que S ( N ), o que contradiz a definição da função S ( n ).
A incomputabilidade de Σ ( n ) pode ser provada de maneira semelhante. Na prova acima, deve-se trocar a máquina EvalS por EvalΣ e Limpar com Incremento - uma TM simples, procurando um primeiro 0 na fita e substituindo-o por 1.
A incomputabilidade de S ( n ) também pode ser estabelecida por referência ao problema de parada da fita em branco. O problema da parada da fita em branco é o problema de decidir para qualquer máquina de Turing se ela irá parar ou não quando iniciada em uma fita vazia. O problema da parada da fita em branco é equivalente ao problema da parada padrão e, portanto, também é incomputável. Se S ( n ) fosse computável, poderíamos resolver o problema de parada da fita em branco simplesmente executando qualquer máquina de Turing com n estados para S ( n ) etapas; se ainda não parou, nunca o fará. Portanto, uma vez que o problema de parada da fita em branco não é computável, segue-se que S ( n ) também deve ser incomputável.
Generalizações
Para qualquer modelo de computação , existem análogos simples do castor ocupado. Por exemplo, a generalização para máquinas de Turing com n estados e de m símbolos define as seguintes funções castor ocupado generalizadas :
- Σ ( n , m ): o maior número de não zeros imprimíveis por um n-estado , máquina de símbolo m iniciado em uma fita inicialmente em branco antes de parar, e
- S ( n , m ): o maior número de passos dados por um n -state, m -symbol máquina iniciado em uma fita inicialmente em branco antes de parar.
Por exemplo, a máquina de 3 estados e 3 símbolos de longa duração encontrada até agora funciona 119 112 334 170 342 540 etapas antes de parar. A máquina de 6 estados e 2 símbolos de execução mais longa, que tem a propriedade adicional de reverter o valor da fita em cada etapa, produz6147 1s depois47 339 970 passos. Então S RTM (6) ≥47 339 970 e Σ RTM (6) ≥6147 .
É possível generalizar ainda mais a função do castor ocupado estendendo a mais de uma dimensão.
Da mesma forma, poderíamos definir uma função análoga à Σ para máquinas de registro como o maior número que pode estar presente em qualquer registro na parada, para um determinado número de instruções.
Valores exatos e limites inferiores
A tabela a seguir lista os valores exatos e alguns limites inferiores conhecidos para S ( n , m ) e Σ ( n , m ) para os problemas generalizados do castor ocupado. Nota: entradas listadas como "?" são limitados a partir de baixo pelo máximo de todas as entradas à esquerda e acima. Essas máquinas não foram investigadas ou foram subseqüentemente superadas por uma máquina menor.
As máquinas de Turing que alcançam esses valores estão disponíveis na página de Pascal Michel . Cada um desses sites também contém algumas análises das máquinas de Turing e referências às provas dos valores exatos.
Valores de S ( n , m ) nm2 estados 3 estados 4 estados 5 estados 6 estados 7 estados 2-símbolo 6 21 107 47 176 870 ? > 7,4 × 10 36 534 > 10 10 10 1018 705 353 3-símbolo 38 ≥ 119 112 334 170 342 540 > 1,0 × 10 14 072 ? ? ? 4-símbolo ≥ 3 932 964 > 5,2 × 10 13 036 ? ? ? ? 5-símbolo > 1,9 × 10 704 ? ? ? ? ? 6-símbolo > 2,4 × 10 9866 ? ? ? ? ? Valores de Σ ( n , m ) nm2 estados 3 estados 4 estados 5 estados 6 estados 7 estados 2-símbolo 4 6 13 4098 ? > 3,5 × 10 18 267 > 10 10 10 1018 705 353 3-símbolo 9 ≥ 374 676 383 > 1,3 × 10 7036 ? ? ? 4-símbolo ≥ 2050 > 3,7 × 10 6518 ? ? ? ? 5-símbolo > 1,7 × 10 352 ? ? ? ? ? 6-símbolo > 1,9 × 10 4933 ? ? ? ? ?
Máquinas de Turing não determinísticas
| p | degraus | estados |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 6 | 7 |
| 4 | 7 | 11 |
| 5 | 8 | 15 |
| 6 | 7 | 18 |
| 7 | 6 | 18 |
O problema pode ser estendido para máquinas de Turing não determinísticas , procurando o sistema com o maior número de estados em todas as ramificações ou a ramificação com o maior número de etapas. A questão de saber se um determinado NDTM irá parar ainda é computacionalmente irredutível, e o cálculo necessário para encontrar um castor ocupado NDTM é significativamente maior do que o caso determinístico, uma vez que há vários ramos que precisam ser considerados. Para um sistema de 2 estados e 2 cores com p casos ou regras, a tabela à direita fornece o número máximo de etapas antes de parar e o número máximo de estados exclusivos criados pelo NDTM.
Formulários
Além de representar um jogo matemático bastante desafiador , as funções do castor ocupado oferecem uma abordagem totalmente nova para resolver problemas de matemática pura. Muitos problemas abertos em matemática poderiam, em teoria, mas não na prática, ser resolvidos de forma sistemática, dado o valor de S ( n ) para um n suficientemente grande .
Considere qualquer conjectura que possa ser refutada por meio de um contra - exemplo entre um número contável de casos (por exemplo, a conjectura de Goldbach ). Escreva um programa de computador que teste sequencialmente essa conjectura para valores crescentes. No caso da conjectura de Goldbach, consideraríamos todo número par ≥ 4 sequencialmente e testaríamos se é ou não a soma de dois números primos. Suponha que este programa seja simulado em uma máquina de Turing de n estados. Se encontrar um contra-exemplo (um número par ≥ 4 que não é a soma de dois primos em nosso exemplo), ele para e indica isso. No entanto, se a conjectura for verdadeira, nosso programa nunca será interrompido. (Este programa só é interrompido se encontrar um contra-exemplo.)
Agora, este programa é simulado por uma máquina de Turing de n- estados, portanto, se soubermos S ( n ), podemos decidir (em um período de tempo finito) se ele irá parar ou não simplesmente rodando a máquina em tantos passos. E se, após S ( n ) passos, a máquina não parar, sabemos que ela nunca irá parar e, portanto, não há contra-exemplos para a conjectura dada (ou seja, nenhum número par que não seja a soma de dois primos). Isso provaria que a conjectura é verdadeira.
Assim, valores específicos (ou limites superiores) para S ( n ) poderiam ser usados para resolver sistematicamente muitos problemas abertos em matemática (em teoria). No entanto, os resultados atuais sobre o problema do castor ocupado sugerem que isso não será prático por dois motivos:
- É extremamente difícil provar valores para a função de castor ocupado (e a função de deslocamento máximo). Só foi comprovado para máquinas extremamente pequenas com menos de cinco estados, enquanto um presumivelmente precisaria de pelo menos 20-50 estados para fazer uma máquina útil. Além disso, cada valor exato conhecido de S ( n ) foi provado pela enumeração de cada máquina de Turing de n- estados e pela comprovação se cada uma para ou não. Seria necessário calcular S ( n ) por algum método menos direto para que ele fosse realmente útil.
- Mas mesmo que alguém encontrasse uma maneira melhor de calcular S ( n ), os valores da função do castor ocupado (e da função de deslocamento máximo) ficam muito grandes, muito rápido. S (6)> 1036 534 já requer aceleração baseada em padrão especial para ser capaz de simular até a conclusão. Da mesma forma, sabemos que S (10)> Σ (10)> 3 ↑↑↑ 3 é um número gigantesco e S (17)> Σ (17)> G, onde G é o número de Graham - um número enorme. Assim, mesmo que soubéssemos, digamos, S (30), é completamente irracional executar qualquer máquina nesse número de etapas. Não há capacidade computacional suficiente na parte conhecida do universo para realizar até mesmo S (6) operações diretamente.
Instâncias notáveis
Uma máquina de Turing binária de 748 estados foi construída para parar se o ZFC for inconsistente. Uma máquina de Turing de 744 estados foi construída para parar se a hipótese de Riemann for falsa. Uma máquina de Turing de 43 estados foi construída para interromper se a conjectura de Goldbach for falsa, e uma máquina de 27 estados para essa conjectura foi proposta, mas ainda não foi verificada.
Uma máquina de Turing de 15 estados foi construída para parar se a seguinte conjectura formulada por Paul Erdős em 1979 for falsa: para todo n> 8 há pelo menos um dígito 2 na representação de base 3 de 2 n .
Exemplos
Estas são tabelas de regras para as máquinas de Turing que geram Σ (1) e S (1), Σ (2) e S (2), Σ (3) (mas não S (3)), Σ (4) e S (4), e o limite inferior mais conhecido para Σ (5) e S (5), e Σ (6) e S (6). Para outras visualizações,
Nas tabelas, as colunas representam o estado atual e as linhas representam o símbolo atual lido da fita. Cada entrada da tabela é uma sequência de três caracteres, indicando o símbolo a ser escrito na fita, a direção do movimento e o novo estado (nessa ordem). O estado de interrupção é mostrado como H .
Cada máquina começa no estado A com uma fita infinita que contém todos os 0s. Assim, o símbolo inicial lido da fita é 0.
Chave Resultado: (começa na posição sublinhadas , paradas na posição sublinhada )
Castor ocupado de 1 estado, 2 símbolos UMA 0 1R H 1 (não usado)
Resultado: 0 0 1 0 0 (1 etapa, um total de "1")
Castor ocupado de 2 estados, 2 símbolos UMA B 0 1R B 1L A 1 1L B 1R H
Resultado: 0 0 1 1 1 1 0 0 (6 etapas, quatro "1" no total)
Castor ocupado de 3 estados, 2 símbolos UMA B C 0 1R B 0R C 1L C 1 1R H 1R B 1L A
Resultado: 0 0 1 1 1 1 1 1 0 0 (14 passos, seis "1" s no total).
Ao contrário das máquinas anteriores, este é um castor ocupado apenas para Σ, mas não para S . ( S (3) = 21)
Castor ocupado de 4 estados, 2 símbolos UMA B C D 0 1R B 1L A 1R H 1R D 1 1L B 0L C 1L D 0R A
Resultado: 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 (107 passos, treze "1" s no total)
atual 5 estados, 2 símbolos, o melhor candidato (possível castor ocupado) UMA B C D E 0 1R B 1R C 1R D 1L A 1R H 1 1L C 1R B 0L E 1L D 0L A
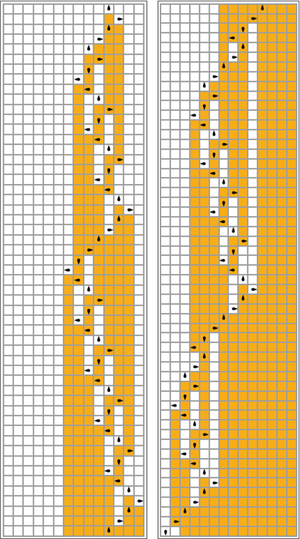
Resultado: 4098 "1" s com 8.191 "0" s intercalados em 47.176.870 etapas.
Observe na imagem à direita como esta solução é qualitativamente semelhante à evolução de alguns autômatos celulares .
atual melhor candidato com 6 estados e 2 símbolos UMA B C D E F 0 1R B 1R C 1L D 1R E 1L A 1L H 1 1L E 1R F 0R B 0L C 0R D 1R C
Resultado: ± 3,515 × 10 18267 "1" s em ± 7,412 × 10 36534 etapas.
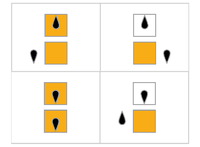
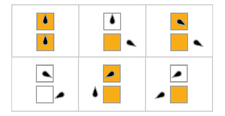
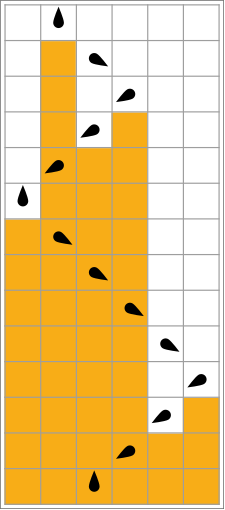
Visualizações
Na tabela a seguir, as regras para cada castor ocupado (maximizando Σ) são representadas visualmente, com quadrados laranja correspondendo a um "1" na fita e brancos correspondendo a "0". A posição da cabeça é indicada pelo ovoide preto, com a orientação da cabeça representando o estado. As fitas individuais são dispostas horizontalmente, com o tempo progredindo verticalmente. O estado de parada é representado por uma regra que mapeia um estado para si mesmo (a cabeça não se move).
Veja também
Notas
- ^ a b Radó, Tibor (maio de 1962). "Sobre funções não computáveis" (PDF) . Bell System Technical Journal . 41 (3): 877–884. doi : 10.1002 / j.1538-7305.1962.tb00480.x .
- ^ Chaitin (1987)
- ^ Adam Yedidia e Scott Aaronson (maio de 2016). Uma máquina de Turing relativamente pequena cujo comportamento é independente da teoria dos conjuntos (relatório técnico). MIT. arXiv : 1605.04343 . Bibcode : 2016arXiv160504343Y .
- ^ Aron, Jacob. "Esta máquina de Turing deve funcionar para sempre, a menos que a matemática esteja errada" . Página visitada em 25/09/2016 .
- ^ a b A versão de 3 de maio continha 7918 estados: "O número 8000th Busy Beaver ilude a teoria do conjunto ZF" . Blog otimizado por Shtetl . 03/05/2016 . Página visitada em 25/09/2016 .
- ^ a b c "Três anúncios" . Blog otimizado por Shtetl . 03/05/2016 . Página visitada em 27/04/2018 .
- ^ "GitHub - sorear / metamath-turing-machines: enumeradores à prova de metamath e outras coisas" . 13/02/2019.
- ^ "The Busy Beaver Frontier" (PDF) .
- ^ "Página do esqueleto para o problema do Busy Beaver" . skelet.ludost.net .
- ^ Turing: Um Projeto para Concluir o Busy Beaver of 5
- ^ "O problema do castor ocupado: UM NOVO ATAQUE DO MILÊNIO" .
- ^ a b Wolfram, Stephen (4 de fevereiro de 2021). "Máquinas de Turing Multiway" . www.wolframphysics.org .
- ^ Chaitin 1987
- ^ Lloyd 2001. Capacidade computacional do universo .
- ^ a b c Pavlus, John (10 de dezembro de 2020). "Como os programas de computador mais lentos iluminam os limites fundamentais da matemática" . Quanta Magazine . Recuperado em 2020-12-11 .
- ^ Tristan Stérin e Damien Woods (julho de 2021). Sobre a dureza de saber os valores do castor ocupado BB (15) e BB (5,4) (Relatório Técnico). Maynooth University. arXiv : 2107,12475 .
- ^ Erdõs, Paul (1979). "Alguns problemas não convencionais na teoria dos números" . Matemática. Mag. 52 (2): 67–70. doi : 10.1080 / 0025570X.1979.11976756 .
- ^ Lin, Shen; Rado, Tibor (abril de 1965). "Estudos de computador de problemas da máquina de Turing" . Jornal do ACM . 12 (2): 196–212. doi : 10.1145 / 321264.321270 . S2CID 17789208 .
Referências
-
Radó, Tibor (maio de 1962). "Sobre funções não computáveis" (PDF) . Bell System Technical Journal . 41 (3): 877–884. doi : 10.1002 / j.1538-7305.1962.tb00480.x .
- Foi aqui que Radó definiu pela primeira vez o problema do castor ocupado e provou que ele era incomputável e crescia mais rápido do que qualquer função computável.
-
Lin, Shen; Radó, Tibor (abril de 1965). "Computer Studies of Turing Machine Problems" . Jornal do ACM . 12 (2): 196–212. doi : 10.1145 / 321264.321270 . S2CID 17789208 .
- Os resultados deste trabalho já haviam aparecido em parte na tese de doutorado de Lin de 1963, sob a orientação de Radó. Lin & Radó provam que Σ (3) = 6 e S (3) = 21 provando que todas as Máquinas de Turing de 3 estados e 2 símbolos que não param dentro de 21 passos nunca irão parar. (A maioria é comprovada automaticamente por um programa de computador, no entanto, 40 são comprovados por inspeção humana.)
-
Brady, Allen H. (abril de 1983). "A determinação do valor da função não computável de Rado Σ ( k ) para máquinas de Turing de quatro estados" . Matemática da Computação . 40 (162): 647–665. doi : 10.1090 / S0025-5718-1983-0689479-6 . JSTOR 2007539 .
- Brady prova que Σ (4) = 13 e S (4) = 107. Brady define duas novas categorias para Máquinas de Turing de 3 estados e 2 símbolos sem interrupção: Árvores de Natal e Contadores. Ele usa um programa de computador para provar que todas as máquinas, exceto 27, que executam mais de 107 etapas, são variantes de árvores de Natal e contadores que podem funcionar infinitamente. As últimas 27 máquinas (conhecidas como resistências) foram comprovadas por inspeção pessoal pelo próprio Brady para não parar.
-
Machlin, Rona; Stout, Quentin F. (junho de 1990). “O comportamento complexo das máquinas simples” . Physica D: Nonlinear Phenomena . 42 (1–3): 85–98. Bibcode : 1990PhyD ... 42 ... 85M . doi : 10.1016 / 0167-2789 (90) 90068-Z . hdl : 2027,42 / 28528 .
- Machlin e Stout descrevem o problema do castor ocupado e muitas técnicas usadas para localizar castores ocupados (que eles aplicam a Máquinas de Turing com 4 estados e 2 símbolos, verificando assim a prova de Brady). Eles sugerem como estimar uma variante da probabilidade de parada de Chaitin (Ω).
-
Marxen, Heiner; Buntrock, Jürgen (fevereiro de 1990). "Atacando o Castor Ocupado 5" . Boletim do EATCS . 40 : 247–251. Arquivado do original em 09/10/2006 . Recuperado em 2020-01-19 .
- Marxen e Buntrock demonstram que Σ (5) ≥ 4098 e S (5) ≥ 47 176 870 e descrever em detalhes o método que eles usaram para encontrar essas máquinas e provar que muitas outras nunca pararão.
- Green, Milton W. (1964). Um limite inferior na função Sigma de Rado para máquinas de Turing binárias . 1964 Proceedings of the Fifth Annual Symposium on Switching Circuit Theory and Logical Design . pp. 91–94. doi : 10.1109 / SWCT.1964.3 .
-
Dewdney, Alexander K. (1984). "Uma armadilha de computador para o castor ocupado, a máquina de Turing que mais trabalha". Scientific American . 251 (2): 10–17.
- Os programas de castores ocupados são descritos por Alexander Dewdney em Scientific American , agosto de 1984, páginas 19-23, também março de 1985 p. 23 e abril de 1985 p. 30 .
- Chaitin, Gregory J. (1987). "Computing the Busy Beaver Function" (PDF) . Na capa, TM; Gopinath, B. (eds.). Problemas abertos em comunicação e computação . Springer. pp. 108-112. ISBN 978-0-387-96621-2.
-
Brady, Allen H. (1995). "O jogo do castor ocupado e o sentido da vida". Em Herken, Rolf (ed.). The Universal Turing Machine: A Half-Century Survey (2ª ed.). Wien, New York: Springer-Verlag. pp. 237–254. ISBN 978-3-211-82637-9.
- Onde Brady (de fama em 4 estados) descreve um pouco da história da besta e chama sua busca de "O Jogo do Castor Ocupado". Ele descreve outros jogos (por exemplo, autômatos celulares e Jogo da Vida de Conway ). De particular interesse é "The Busy Beaver Game in Two Dimensions" (p. 247). Com 19 referências.
-
Booth, Taylor L. (1967). Máquinas Seqüenciais e Teoria dos Autômatos . Nova York: Wiley. ISBN 978-0-471-08848-6.
- Cf Capítulo 9, Máquinas de Turing. Um livro difícil, destinado a engenheiros elétricos e especialistas técnicos. Discute recursão, recursão parcial com referência a Máquinas de Turing, problema de parada. Uma referência em Booth atribui castor ocupado a Rado. Booth também define o problema do castor ocupado de Rado em "problemas domésticos" 3, 4, 5, 6 do Capítulo 9, p. 396. O problema 3 é "mostrar que o problema do castor ocupado não tem solução ... para todos os valores de n."
-
Ben-Amram, AM; Julstrom, BA; Zwick, U. (1996). "Uma nota sobre os castores ocupados e outras criaturas" . Teoria Matemática de Sistemas . 29 (4): 375–386. CiteSeerX 10.1.1.75.1297 . doi : 10.1007 / BF01192693 . S2CID 30937913 .
- Limites entre as funções Σ e S .
-
Ben-Amram, AM; Petersen, H. (2002). "Limites aprimorados para funções relacionadas a Busy Beavers". Teoria de Sistemas Computacionais . 35 : 1-11. CiteSeerX 10.1.1.136.5997 . doi : 10.1007 / s00224-001-1052-0 . S2CID 10429773 .
- Limites aprimorados.
-
Lafitte, G .; Papazian, C. (junho de 2007). "O tecido das pequenas máquinas de Turing". Computation and Logic in the Real World, Proceedings of the Third Conference on Computability in Europe . pp. 219-227. CiteSeerX 10.1.1.104.3021 .
- Este artigo contém uma classificação completa das máquinas de Turing de 2 estados e 3 símbolos e, portanto, uma prova para o castor ocupado (2, 3): Σ (2, 3) = 9 e S (2, 3) = 38.
- Boolos, George S .; Burgess, John P .; Jeffrey, Richard C. (2007). Computabilidade e Lógica (Quinta ed.). Cambridge University Press. ISBN 978-0-521-87752-7.
-
Kropitz, Pavel (2010). Problém Busy Beaver (dissertação de bacharelado) (em eslovaco). Charles University em Praga.
- Esta é a descrição das ideias, dos algoritmos e sua implementação, com a descrição dos experimentos examinando máquinas de Turing de 5 e 6 estados por execução paralela em 31 computadores de 4 núcleos e, finalmente, os melhores resultados para a TM de 6 estados.
links externos
- A página de Heiner Marxen , que, com Jürgen Buntrock, encontrou os registros mencionados acima para uma máquina de Turing de 5 e 6 estados.
- Pesquisa histórica de Pascal Michel de resultados de castores ocupados, que também contém os melhores resultados e algumas análises.
- Definição da classe RTM - Reversal Turing Machines, subclasse simples e forte das TMs.
- O " Ataque Millennium " no Laboratório Rensselaer RAIR sobre o problema do castor. Este esforço encontrou vários novos registros e estabeleceu vários valores para a formalização quádrupla.
- Arquivo do site de Daniel Briggs e fórum para resolver o problema do castor ocupado de 5 estados e 2 símbolos, com base na lista de máquinas não regulares do Skelet (Georgi Georgiev).
- Aaronson, Scott (1999), Quem pode citar o maior número?
- Weisstein, Eric W. "Busy Beaver" . MathWorld .
- Busy Beaver Turing Machines - Computerphile
- Pascal Michel. The Busy Beaver Competition: um levantamento histórico . 70 páginas. 2017. <hal-00396880v5>