Automorfismo - Automorphism
Em matemática , um automorfismo é um isomorfismo de um objeto matemático para si mesmo. É, em certo sentido, uma simetria do objeto e uma maneira de mapear o objeto para si mesmo, preservando toda a sua estrutura. O conjunto de todos os automorfismos de um objeto forma um grupo , denominado grupo de automorfismos . É, falando vagamente, o grupo de simetria do objeto.
Definição
No contexto da álgebra abstrata , um objeto matemático é uma estrutura algébrica , como um grupo , anel ou espaço vetorial . Um automorfismo é simplesmente um homomorfismo bijetivo de um objeto consigo mesmo. (A definição de um homomorfismo depende do tipo de estrutura algébrica; veja, por exemplo, homomorfismo de grupo , homomorfismo de anel e operador linear ).
O morfismo de identidade ( mapeamento de identidade ) é denominado automorfismo trivial em alguns contextos. Respectivamente, outros automorfismos (de não identidade) são chamados de automorfismos não triviais .
A definição exata de um automorfismo depende do tipo de "objeto matemático" em questão e do que, precisamente, constitui um "isomorfismo" desse objeto. O cenário mais geral em que essas palavras têm significado é um ramo abstrato da matemática chamado teoria das categorias . A teoria das categorias lida com objetos abstratos e morfismos entre esses objetos.
Na teoria das categorias, um automorfismo é um endomorfismo (ou seja, um morfismo de um objeto para si mesmo) que também é um isomorfismo (no sentido categórico da palavra, o que significa que existe um endomorfismo inverso à direita e à esquerda).
Esta é uma definição muito abstrata, pois, na teoria das categorias, morfismos não são necessariamente funções e objetos não são necessariamente conjuntos. Na maioria dos ambientes concretos, no entanto, os objetos serão conjuntos com alguma estrutura adicional e os morfismos serão funções que preservam essa estrutura.
Grupo de automorfismo
Se os automorfismos de um objeto X formam um conjunto (ao invés de uma classe própria ), então eles formam um grupo sob composição de morfismos . Este grupo é chamado o grupo automorphism de X .
- Fecho
- A composição de dois automorfismos é outro automorfismo.
- Associatividade
- Faz parte da definição de uma categoria que a composição dos morfismos seja associativa.
- Identidade
- A identidade é o morfismo da identidade de um objeto para si mesmo, que é um automorfismo.
- Inversos
- Por definição, todo isomorfismo tem um inverso que também é um isomorfismo e, como o inverso também é um endomorfismo do mesmo objeto, é um automorfismo.
O grupo de automorfismo de um objeto X em uma categoria C é denotado como Aut C ( X ), ou simplesmente Aut ( X ) se a categoria for clara no contexto.
Exemplos
- Na teoria dos conjuntos , uma permutação arbitrária dos elementos de um conjunto X é um automorfismo. O grupo automorphism de X também é chamado o grupo simétrico em X .
- Na aritmética elementar , o conjunto de inteiros , Z , considerado como um grupo em adição, tem um automorfismo não trivial único: negação. Considerado como um anel, porém, possui apenas o automorfismo trivial. De modo geral, a negação é um automorfismo de qualquer grupo abeliano , mas não de um anel ou campo.
- Um automorfismo de grupo é um isomorfismo de grupo de um grupo para si mesmo. Informalmente, é uma permutação dos elementos do grupo de forma que a estrutura permanece inalterada. Para cada grupo G existe um homomorfismo natural Grupo G → Aut ( G ), cuja imagem é o grupo Inn ( G ) de automorfismos internos e cujo núcleo é o centro de G . Assim, se G tiver um centro trivial , ele pode ser embutido em seu próprio grupo de automorfismo.
- Em álgebra linear , um endomorfismo de um espaço vector V é um operador linear V → V . Um automorphism é um operador linear invertível em V . Quando o espaço vetorial é finito-dimensional, o grupo de automorfismo de V é igual ao grupo linear geral , GL ( V ). (A estrutura algébrica de todos os endomorfismos de V é ela própria uma álgebra sobre o mesmo campo de base de V , cujos elementos invertíveis consistem precisamente em GL ( V ).)
- Um automorphism campo é um bijective homomorphism anel a partir de um campo para si. Nos casos dos números racionais ( Q ) e dos números reais ( R ), não há automorfismos de campo não triviais. Alguns subcampos de R têm automorfismos de campo não triviais, os quais, entretanto, não se estendem a todos os R (porque eles não podem preservar a propriedade de um número com uma raiz quadrada em R ). No caso dos números complexos , C , há um automorfismo não trivial único que envia R em R : conjugação complexa , mas há infinitamente ( incontáveis ) muitos automorfismos "selvagens" (assumindo o axioma da escolha ). Os automorfismos de campo são importantes para a teoria das extensões de campo , em particular as extensões de Galois . No caso de uma extensão de Galois L / K, o subgrupo de todos os automorfismos de L fixando K no ponto é chamado de grupo de Galois da extensão.
- O grupo de automorfismo dos quatérnions ( H ) como um anel são os automorfismos internos, pelo teorema de Skolem-Noether : mapas da forma a ↦ bab −1 . Este grupo é isomórfico a SO (3) , o grupo de rotações no espaço tridimensional.
- O grupo de automorfismo das octonions ( O ) é o grupo de Lie excepcional G 2 .
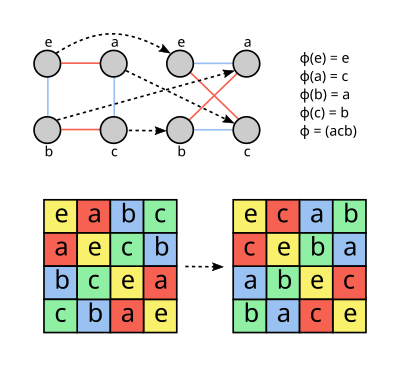
- Na teoria dos grafos, um automorfismo de um grafo é uma permutação dos nós que preserva as arestas e não arestas. Em particular, se dois nós são unidos por uma aresta, o mesmo ocorre com suas imagens sob a permutação.
- Em geometria , um automorfismo pode ser chamado de movimento do espaço. Terminologia especializada também é usada:
- Em geometria métrica, um automorfismo é uma autoisometria . O grupo de automorfismo também é chamado de grupo de isometria .
- Na categoria de superfícies de Riemann , um automorfismo é um mapa biolomórfico (também chamado de mapa conformal ), de uma superfície para si mesmo. Por exemplo, os automorfismos da esfera de Riemann são transformações de Möbius .
- Um automorfismo de uma variedade diferenciável M é um difeomorfismo de M para si mesmo. O grupo de automorfismo às vezes é denominado Diff ( M ).
- Em topologia , morfismos entre espaços topológicos são chamados de mapas contínuos , e um automorfismo de um espaço topológico é um homeomorfismo do espaço para si mesmo, ou auto-homeomorfismo (ver grupo homeomorfismo ). Neste exemplo, não é suficiente que um morfismo seja bijetivo para ser um isomorfismo.
História
Um dos primeiros automorfismos de grupo (automorfismo de um grupo, não simplesmente um grupo de automorfismos de pontos) foi dado pelo matemático irlandês William Rowan Hamilton em 1856, em seu cálculo icosiano , onde ele descobriu um automorfismo de ordem dois, escrevendo:
de modo que essa é uma nova quinta raiz de unidade, conectada com a antiga quinta raiz por relações de reciprocidade perfeita.
Automorfismos internos e externos
Em algumas categorias - principalmente grupos , anéis e álgebras de Lie - é possível separar os automorfismos em dois tipos, chamados automorfismos "internos" e "externos".
No caso de grupos, os automorfismos internos são as conjugações dos elementos do próprio grupo. Para cada elemento a de um grupo G , a conjugação por a é a operação φ a : G → G dada por φ a ( g ) = aga −1 (ou a −1 ga ; o uso varia). Pode-se verificar facilmente que a conjugação por a é um automorfismo de grupo. Os automorfismos internos formam um subgrupo normal de Aut ( G ), denotado por Inn ( G ); isso é chamado de lema de Goursat .
Os outros automorfismos são chamados de automorfismos externos . O grupo quociente Aut ( G ) / Inn ( G ) é geralmente denotado por Out ( G ); os elementos não triviais são os cosets que contêm os automorfismos externos.
A mesma definição vale para qualquer anel unital ou álgebra onde a é qualquer elemento invertível . Para álgebras de Lie, a definição é ligeiramente diferente.
Veja também
- Antiautomorfismo
- Automorfismo (em quebra-cabeças de Sudoku)
- Subgrupo de características
- Anel de endomorfismo
- Automorfismo de Frobenius
- Morfismo
- Automorfismo de ordem (na teoria da ordem ).
- Automorfismo de preservação de relação
- Transformada fracionária de Fourier
Referências
- ^ PJ Pahl, R Damrath (2001). "§7.5.5 Automorfismos" . Fundamentos matemáticos da engenharia computacional (tradução de Felix Pahl ed.). Springer. p. 376. ISBN 3-540-67995-2.
- ^ Yale, Paul B. (maio de 1966). "Automorfismos dos Números Complexos" (PDF) . Revista Matemática . 39 (3): 135–141. doi : 10.2307 / 2689301 . JSTOR 2689301 .
- ^ Lounesto, Pertti (2001), Clifford Algebras and Spinors (2ª ed.), Cambridge University Press, pp. 22-23, ISBN 0-521-00551-5
- ^ Handbook of algebra , 3 , Elsevier , 2003, p. 453
- ^ Senhor William Rowan Hamilton (1856). "Memorando respeitando um novo sistema de raízes da unidade" (PDF) . Revista Filosófica . 12 : 446.


